基于改進混合差分進化算法的輸電網規劃研究

黃 映

(南京供電公司，江蘇南京210019)

輸電網絡擴展規劃是根據負荷增長、電源規劃方案以及現有網絡結構和參數，確定輸電網絡的最佳擴展方案，以滿足安全運行和經濟性最優[1]。從數學上講，電網擴展規劃是一個帶有大量約束條件的非線性整數規劃問題，計算較復雜。鑒于輸電網擴展規劃問題的重要性，各國學者對其提出了許多求解方法，主要分為啟發式方法、數學優化類方法[2]和智能優化方法三類[3，4]。

差分進化算法[5]（DE）是Storn和Price在1995年提出的一種在連續空間中進行啟發式隨機搜索的優化算法。該算法直接采用實數直接運算，不需要編碼和解碼操作，收斂速度快，穩定性好，其性能被證明要優于其他進化算法[6]。目前DE已成功應用于求解經濟負荷分配[7]、無功優化[8]、變電站選址定容[9]等電力系統優化問題。雖然DE算法實現簡單、收斂快速，但是該算法以隨機概率選取試驗個體進行進化，容易陷入局部最優，出現早熟收斂現象，若通過增加種群規模以提高種群多樣性的方式會降低算法的收斂速度。為改善DE的性能，更好地解決電網規劃問題，本文構造一種改進的混合差分進化算法（IHDE），進一步提高算法的收斂速度和全局尋優性能，并以Garver-6節點系統和18節點系統算例驗證了此算法的尋優能力。

1 電網規劃數學模型

本文在單階段靜態電網擴展規劃問題中，主要考慮電網擴建的投資費用、固定運行維護費用以及系統年運行費用（即網損費用），在滿足約束條件的情況下使總費用最小，規劃方案能滿足N-1檢驗。其各種費用的計算考慮了資金的時間價值，采用等年值費用法。模型采用的目標函數為：

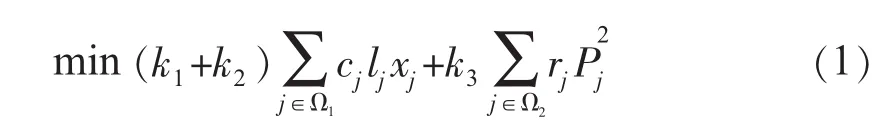
式（1）中：第一項為規劃方案的建設投資費用，萬元；第二項為線路的可變運行費用，用年網損費用表示，萬元。其 中 k1為 資 金 回 收 系 數r為貼現率，%；n為工程經濟使用年限；k2為工程固定運行費用率，%；cj為單位長度線路造價，萬元/km；xj為線路j中新建線路回路數；lj為線路j的長度，km；Ω1為待選新建線路集合；k3為年網損費用系數；這里為網損電價，元 /（kW·h）；τ為最大負荷損耗時間，h；U 為系統額定電壓，kV；rj為線路j的電阻；Pj為正常情況下線路j輸送的有功功率，MW；Ω2為網絡中已有的和新建的線路集合。

模型考慮的約束條件包括系統潮流約束，線路容量約束，輸電走廊最大可建線路約束，其數學表達見文獻[10]。潮流計算采用直流潮流模型。

2 差分進化算法及其改進

2.1 基本差分進化算法

差分進化算法由Np（種群規模）個D（決策變量個數）維參數矢量在搜索空間進行并行直接的搜索。DE的基本操作包括變異、交叉和選擇3種操作。

（1）變異。

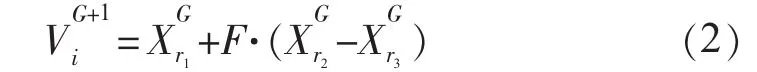
（2） 交叉。

（3）選擇。對于最小化問題，選擇操作可表述為：

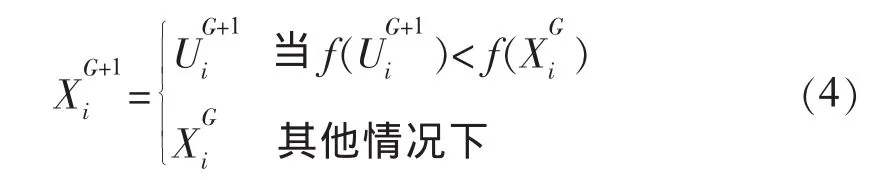
2.2 差分進化算法的改進

DE采用貪婪策略進行選擇操作，雖然加快了算法的收斂速度，但在算法的后期收斂速度較慢,甚至會陷入局部最優出現早熟現象[11]。鑒于此，本文構造一種改進的混合差分進化算法（IHDE），該算法在求解過程中能夠隨進化過程動態調整DE的縮放因子和交叉概率，在保持種群多樣性的同時提高DE的全局尋優能力；而針對DE早熟收斂問題，以種群的適應度方差判斷種群中個體的聚集程度，引入混沌搜索策略，提高算法后期的搜索能力。

（1）控制參數的改進。DE算法的主要控制參數F和CR影響搜索過程的收斂速度和魯棒性，F和CR取值較大可以得到較好的搜索但算法的收斂速度會較慢，取值較小會使算法陷入局部最優。良好的搜索策略應該是在搜索的初始階段保持種群多樣性，進行全局搜索，而在搜索的后期應加強局部搜索能力，以提高算法的精度。本文對F和CR采取根據進化代數動態調整策略，即在算法的初期取較小的F和CR，隨著種群進化，不斷增大兩參數的取值，以保證其收斂性。

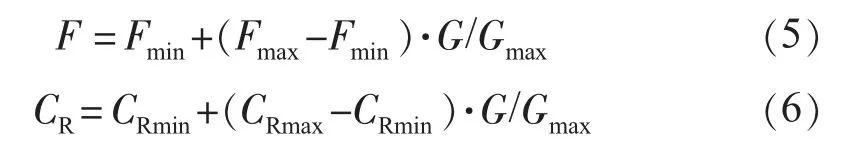
（2）種群適應度方差。隨著種群的不斷進化，個體之間的差異越來越小，而個體位置決定了個體的適應度，根據種群中所有個體的適應度的整體情況可以判斷種群的狀態。種群的適應度方差定義為：

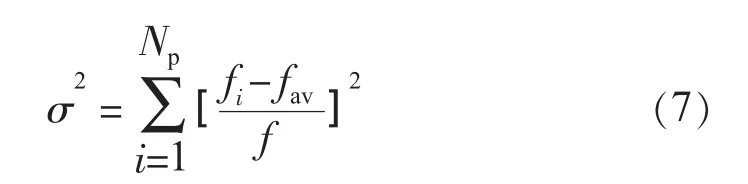
f的取值采用式為：

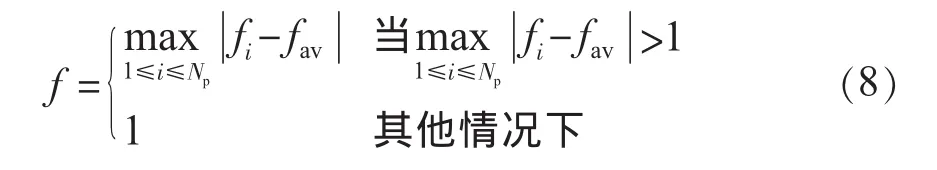
（3）混沌搜索策略。針對早熟收斂現象，本文在DE算法陷入局部最優時對當代最優個體進行混沌搜索，使算法脫離聚集狀態。混沌是自然界廣泛存在的一種非線性現象，由于混沌運動的固有特點及混沌遍歷的規律性及不重復性，使混沌處理方法被廣泛用于處理優化搜索問題[12]。混沌搜索常用的映射方式為線性載波：

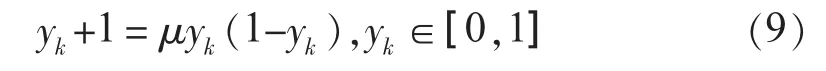
式（9）中：μ為控制參數，其數值直接影響映射情況；k為混沌搜索的迭代次數為混沌變量的各維分量。

2.3 改進混合差分進化算法流程

本文利用混沌搜索機制，并將其融合到差分進化算法中，構造了改進的混合差分算法（IHDE）。其基本思想是基于差分進化機制，動態調整其控制參數，以種群適應度方差判斷算法是否出現早熟收斂現象，若陷入局部最優，則對當代最優個體進行混沌搜索，在搜索達到給定次數后，用混沌搜索得到的最優解隨機替代種群中的個體，從而增強算法的搜索性能。該算法流程如圖1所示。

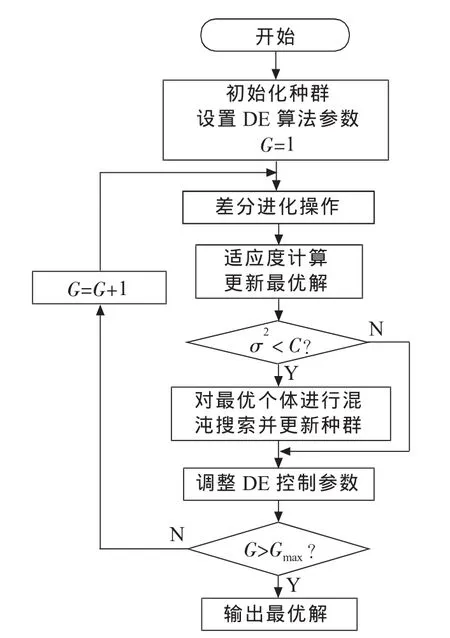
圖1 IHDE算法流程圖

3 基于改進混合差分的電網規劃問題求解

基于上述改進的混合差分進化算法，對第1節描述的單價段輸電網規劃數學模型求解步驟：（1）輸入原始數據。包括網絡拓撲、線路參數、各節點發電出力及負荷以及算法本身需要的控制參數；（2）形成初始種群。本文對n條待選線路走廊的各種可能擴建回路數進行編碼，n條待選線路走廊的擴建回路數集為該線路集構成一個規劃方案，對應于種群中的一個個體；（3）差分進化操作。采用第2.1節中的變異和交叉機制形成新一代種群；（4）個體適應度計算。將每一個體對應的網絡行潮流計算，若個體不滿足約束條件的要求，則通過適應度中的懲罰項將個體自然淘汰，對滿足約束的個體計算方案的投資和網損費用，進而求出個體的適應度值；（5）計算種群適應度方差，若σ2＜C，則對最優個體進行混沌搜索，否則到步驟（6）；（6）根據差分進化代數調整F和CR；（7）如滿足中止條件，則到步驟（8），否則返回到步驟（3）；（8）輸出規劃結果。

4 算例及分析

以修改過的Garver-6節點和18節點系統為算例進行計算與分析，系統中節點數據、支路數據和可擴建走廊數參見文獻[13]和文獻[10]。設資金貼現率r取10%；工程經濟使用年限n為15年，工程固定運行費用率k2為5%，網損電價ρ為0.3元/（kW·h），最大負荷損耗時間τ為3000 h，單位長度線路的投資費用為80萬元/km，取單回線走廊寬度為48.27m，雙回線走廊寬度為68.27m，三回線走廊寬度為88.27m，四回線走廊寬度為108.27m。

以MATLAB2007為仿真環境，對電網規劃問題各進行50次計算，各算法求得平均計算時間和搜索成功率，如表1、表2所示。

6節點系統算例中，本文同時也利用GA，PSO算法進行了編程計算。表1列出各算法對在滿足線路的N-1安全準則的條件下所求得的規劃方案的投資維護費用、網損費用以及綜合費用。其中文獻[14]采用基于適應度函數值共享的小生境改進遺傳算法求解該問題；文獻[15]采用改進的帶雙重變異算子的粒子群算法求解該問題；而文獻[16]采用基于精英策略的非支配排序遺傳算法（NSGA-II），采用投資維護費用、網損費用和“N-1”過負荷量最小的多目標優化方法。文獻[14—16]中3種改進算法的各部分費用均按本文設定的系數進行了折算作為比較。

由于18節點系統是按靜態安全的“N”準則來研究輸電規劃的常用算例，因此對18節點系統設定各線路走廊的可架線路回數為3回，以使規劃方案能夠滿足“N-1”安全準則。18節點系統的2種最優規劃方案見表2，DE算法和本文采用的IHDE算法能夠得到相同的2種最優方案，2種方案下的線路擴建結果雖略有不同，但費用相等。

IHDE和DE算法的種群適應度方差的變化曲線如圖2所示。

由圖2可見，IHDE算法在進化后期對最優個體進行混沌搜索，使種群脫離聚集狀態，拓展了種群的搜索空間，改善了群體適應度方差的分布情況，避免算法陷入早熟收斂，從而有更好的全局尋優能力。

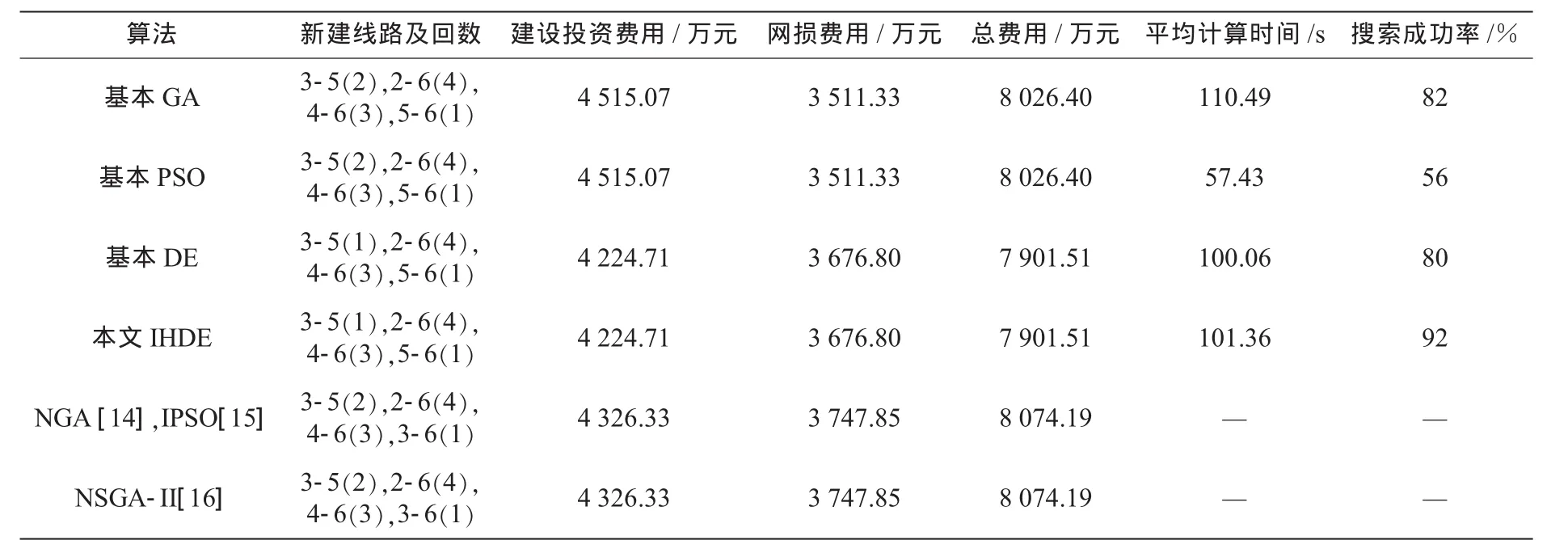
表1 6節點規劃結果

表2 18節點規劃結果

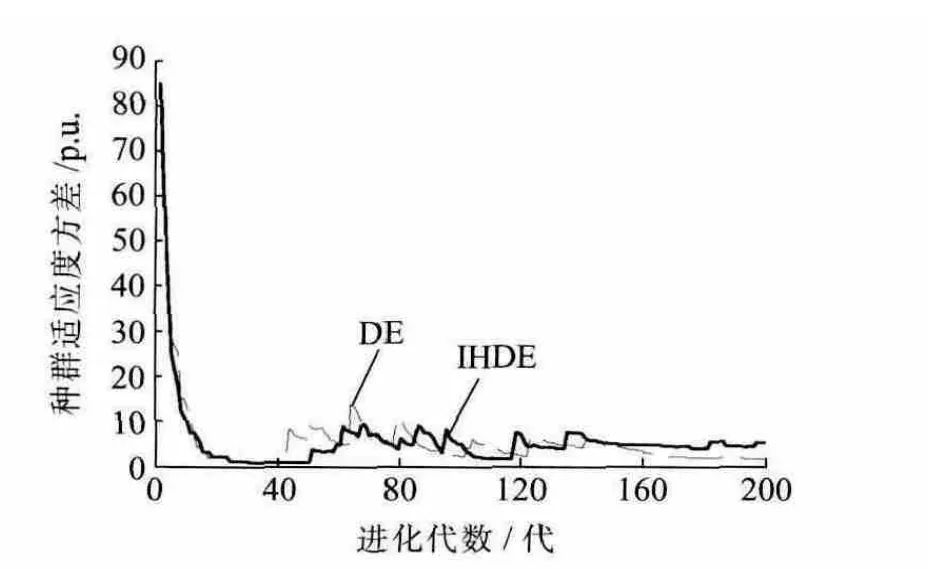
圖2 IHDE和DE算法的群體適應度方差

圖3展示了GA，PSO，DE以及IHDE 4種算法下的電網規劃方案費用隨種群進化代數的變化情況。

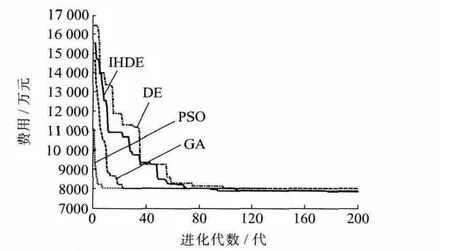
圖3 幾種算法的適應度進化曲線

綜合表1、表2和圖3可見，DE算法本身具有較好的尋優能力和搜索精度，DE及改進的IHDE算法在優化結果和算法性能上（如搜索時間和搜索成功率）都優于GA，PSO算法。比較IHDE算法和基本DE算法，雖然兩者得到的最優結果相同，但是由于IHDE采用了控制參數調整和混沌搜索策略，IHDE算法性能更加穩定，搜索到最優解的成功率明顯高于基本DE算法，且能夠比DE算法更早求得最優解。而由于IHDE算法需要實時跟蹤群體的聚集程度，其計算速度略不如基本DE算法。

5 結束語

本文提出了一種改進的IHDE算法，利用差分進化機制實現簡單、收斂速度快的優點，對基本DE算法進行了改進。該算法能夠隨進化過程動態調整控制參數，進一步提高搜索性能；同時針對算法后期容易陷入局部最優的問題，以種群的適應度方差判斷種群中個體的聚集程度，對最優個體采取混沌搜索。將IHDE算法應用于求解單階段靜態電網規劃問題，通過對修改過的Garver-6節點系統和18節點系統的計算和分析表明，相對GA，PSO和基本DE算法，IHDE算法在搜索效率、計算精度、收斂穩定性、全局尋優能力等方面都有一定的優越性。

[1]麻常輝，薛禹勝，魯庭瑞，等.輸電規劃方法的評述[J].電力系統自動化，2006，30(12)： 97-101.

[2]LATORRE G，CRUZ R D，AREIZA JM，et，al.Classification of Publication and Modelson Transmission Expansion Planning[J].IEEETranson PowerSystems，2003，18(2)： 938-946.

[3]GALLEGO R A，MONTICELLI A，ROMERO R.Transmission System Expansion Planningbyan Extended Genetic Algorithm[J].IEEE Proceedings： Generation，Transmission and Distribution，1998，145(3)： 329-335.

[4]金義雄，程浩忠，嚴健勇，等.基于局優分支優化的粒子群收斂保證算法及其在電網規劃中的應用[J].中國電機工程學報，2005，25(23)：12-18.

[5]STORNR，PRICEK.DifferentialEvolution-a Simpleand Efficient Heuristic forGlobalOptimization OverContinuousSpaces，Technical Report TR-95-012[R].Berkeley：International Computer Science Institute，1995.

[6]MAYERDG，KINGHORNBP，ARCHERA A.DifferentialEvolution-An Easy and Efficient Evolutionary Algorithm for Model Optim ization[J].AgriculturalSystems，2005 ，83(3)：315-328.

[7]NOMAN N，IBA H.Differential Evolution for Economic Load Dispatch Problems[J].Electric Power SystemsResearch，2008，78(8)：1322-1331.

[8]劉自發，閆景信，張建華，等.基于改進微分進化算法的電力系統無功優化[J].電網技術，2007，31(18)：68-72.

[9]牛衛平，劉自發，張建華，等.基于GIS和微分進化算法的變電站選址及定容[J].電力系統自動化，2007，31(18)：82-86.

[10]程浩忠.電力系統規劃[M].北京：中國電力出版社，2008：139-143，259-260.

[11]吳亮紅，王耀南，袁小芳，等.自適應二次變異差分進化算法[J].控制與決策，2006，21(8)： 117-120.

[12]李 兵，蔣慰孫.混沌優化方法及其應用[J].控制理論與應用，1997，14(4)：613-615.

[13]RIDERM J，GAREIA A V.A Constructive Heuristic Algorithm to Short Term Transmission Network Expansion Planning[C].Power Engineering Society General Meeting， 2004 （2）：2107-2113.

[14]張振安，唐國慶.基于小生境技術改進遺傳算法在供電網規劃中的應用[J].江蘇電機工程，2005，24(2)：30-33.

[15]CHEN Y H，CHEN H Y，CHEN JF，et，al.An Improved Particle Swarm Optimization Algorithm for Multistage and Coordinated Planning of Transm ission Systems[C].Transmission and Distribution Conferenceand Exhibition，Asiaand Pacific，2005.

[16]王秀麗，李淑慧，陳皓勇，等.基于非支配遺傳算法及協同進化算法的多目標多區域電網規劃[J].中國電機工程學報，2006，26(12)：11-15.