廣義均衡問題、極大單調算子和全局擬-φ-漸近非擴張半群的公共元的強收斂定理

吳燕林

(陽光學院基礎部, 福建 福州 350015)

廣義均衡問題、極大單調算子和全局擬-φ-漸近非擴張半群的公共元的強收斂定理

吳燕林

(陽光學院基礎部, 福建 福州 350015)

針對廣義均衡問題、 極大單調算子和全局擬-φ-漸近非擴張半群的公共元， 提出一個新的迭代算法， 在適當的條件下， 證明了由此迭代算法生成的序列的強收斂定理.

極大單調算子； 全局擬-φ-漸近非擴張半群; 廣義均衡問題； 公共不動點

0 引言

設E為實的Banach空間，E*為其對偶空間. 設C為E的非空閉凸子集，J:E→2E*為正規對偶映射.

設Φ:C×C→R，A:C→E*. 考慮如下廣義均衡問題(簡記為GEP)， 令u∈C， 使得

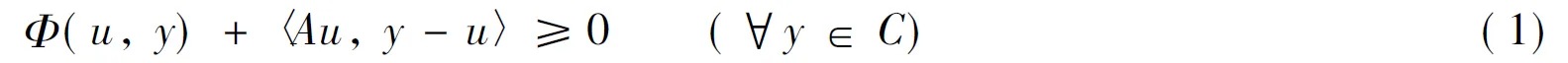
用GEP(Φ)表示(1)式的解集.

眾所周知， 問題(1)有著廣泛的應用， 例如， 變分包含問題、 變分不等式問題、 不動點問題、 最優化問題, 參見文獻[1-3].

假設二元函數Φ:C×C→R滿足下列條件：

(A1)Φ(x,x)=0(?x∈C);

(A2)Φ是單調的, 即Φ(x,y)+Φ(y,x)≤0(?x,y∈C);

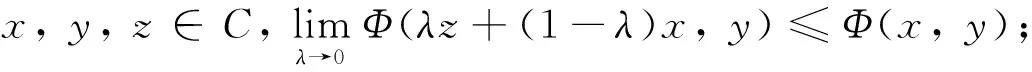
(A4) 對每個x∈C, 函數y|→Φ(x,y)是凸的和下半連續的.

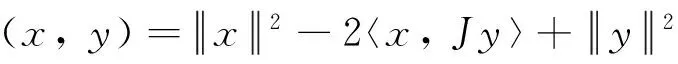
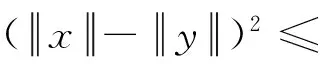
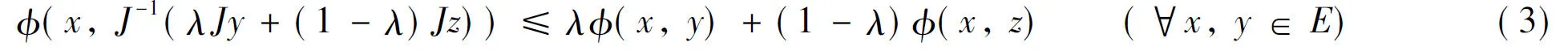
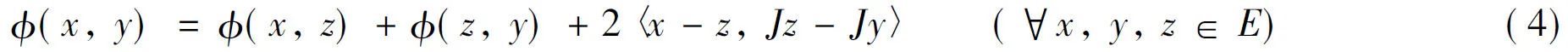
設C為E中的非空閉凸子集， 定義廣義投影算子ΠC:E→C為

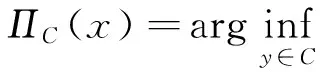
稱T:E→2E*為單調的， 如果滿足〈x-y,x*-y*〉≥0, 其中x*∈Tx,y*∈Ty. 稱T為極大單調的， 如果它的圖像不包含在其它任何單調算子的圖像里. 記T的預解算子為：Jλ:=(J+λT)-1J(?λ>0)， 則Jλ：E→D(T)是單值映射且T-10=F(Jλ)(?λ>0)， 其中D(T)為T的有效域，F(Jλ)表示Jλ的不動點集.

稱Γ:={T(t):C→C;t≥0}為({νn}、 {μn}、ζ)全局擬-φ-漸近非擴張半群， 如果F(Γ)≠?且存在非負的實序列{νn}、 {μn}滿足νn→0，μn→0(n→∞)及嚴格遞增的連續泛函ζ:[0, ∞)→[0, ∞),ζ(0)=0符合下列條件：

1)T(0)x=x(?x∈C)；

2)T(s+t)x=T(s)T(t)x(?s,t≥0, ?x∈C)；

3) 對每一個x∈C， 映射t|→T(t)x在[0, ∞)上都是連續的；

4)φ(p,Tn(t)x)≤φ(p,x)+νnζ(φ(p,x))+μn(?n≥0,x∈C,p∈F(Γ),t≥0)

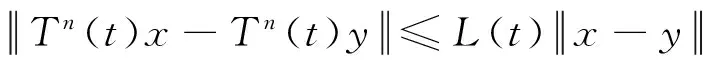
注1[4]設E為一致光滑和嚴格凸的Banach空間,T:E→2E*為極大單調算子且T-10≠?， 則Jλ:=(J+λT)-1J(?λ>0)是從E到D(T)全局擬-φ-漸近非擴張的和閉的.

受到文獻[5-6]的啟發， 本文針對廣義均衡問題， 極大單調算子和全局擬-φ-漸近非擴張半群的公共元， 提出如下算法1：

在適當的條件下， 證明了由算法1生成的序列強收斂于ΠΞ(x0). 其中，Ξ=GEP(Φ)∩T-10∩F(Γ) . 本研究是將文獻[5]的研究對象從相對非擴張映射可數族推廣到全局擬-φ-漸近非擴張半群, 同時將文獻[6]的研究對象從全局擬-φ-漸近非擴張半群拓展到全局擬-φ-漸近非擴張半群公共不動點和廣義均衡問題的解及極大單調算子的零點的公共元問題.

1 預備知識

引理1[7]設E是自反， 嚴格凸和光滑的Banach空間，C為E的非空閉凸子集， 則下面結論成立：

(ⅰ)φ(x,ΠCy)+φ(ΠCy,y)≤φ(x,y)(?x∈C,y∈E)；

(ⅱ) 如果x∈E和z∈C, 則z=ΠCx?〈y-z,Jx-Jz〉≤0(?y∈C)；

(ⅲ) 對任意的x,y∈E，當且僅當x=y時，φ(x,y)=0.

引理2[8]設E是自反， 嚴格凸和光滑的Banach空間，C是E的非空閉凸子集，A:C→E*為α-逆強單調算子， 二元函數Φ:C×C→R滿足(A1)～(A4). 令λ>0， 則對任意的x∈E， 存在u∈C使得

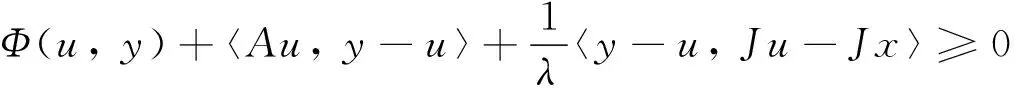
若E為一致光滑的， 定義Tλ:E→C為：

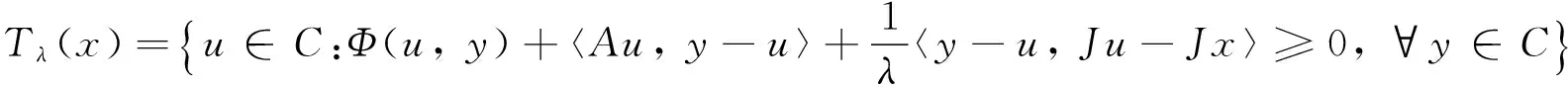
則Tλ滿足下面的性質:

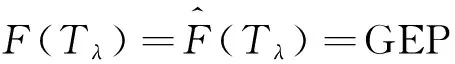
引理3[8-10]設E是自反、 嚴格凸和光滑的Banach空間，T:E→2E*為多值映射， 則如下結論成立：

(ⅰ)φ(z,Jλx)+φ(Jλx,x)≤φ(z,x)(?λ>0,z∈T-10,x∈E);

(ⅱ)Jλ：E→D(T)為相對非擴張映射;

(ⅲ) 如果T是極大單調的和T-10≠?， 則T-10是閉凸的；

(ⅳ)T是極大單調的當且僅當T是單調的且R(J+λT)=E*(?λ>0).

引理4[4]設自反、 嚴格凸和光滑的實Banach空間E和E*都具有Kadec-Klee性質，C為E的非空閉凸子集,T:C→C為({νn}、 {μn}、ζ)全局擬-φ-漸近非擴張映射， 則F(T)是C中的閉凸子集.

3 主要結論

定理1 設光滑、 嚴格凸和自反的實Banach空間E和E*都具有Kadec-Klee性質，C為E的非空閉凸子集. 設A:C→E*為α-逆強單調算子， 二元函數φ:C×C→R滿足條件(A1)～(A4)；T:E→2E*為極大單調算子； 設Γ:={T(t):t≥0}為閉的、 一致Lipschitz和({νn}、 {μn}、ζ)全局擬-φ-漸近非擴張半群， 使得:Ξ≠?. 設序列{λn}?[d, ∞)(d>0)， {αn}?[0, 1)， {βn}?(0， 1)滿足條件：

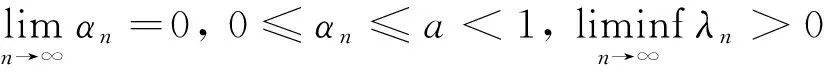
若Ξ在C中有界， 則由算法1生成的序列{xn}強收斂于ΠΞ(x0).

證明 首先， 由Cn定義， 容易證明Cn(n≥0)是C的閉凸子集.

其次， 利用歸納法結合引理2的結論可證Ξ?Cn, ?n≥0.

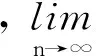
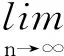
第四， 證明xn→p*(n→∞)(p*是C中的一點).

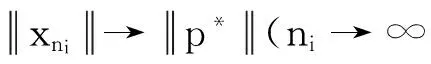
第五， 證明p*∈Ξ.

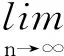
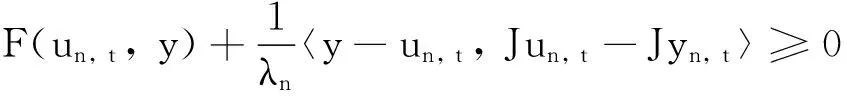
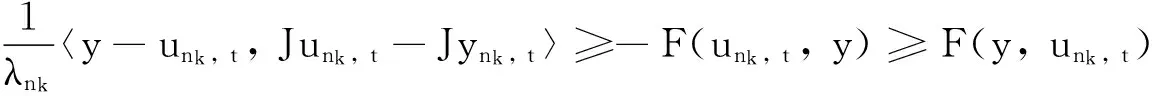
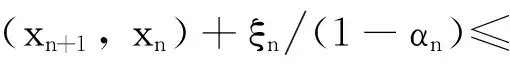
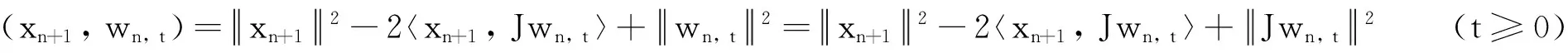
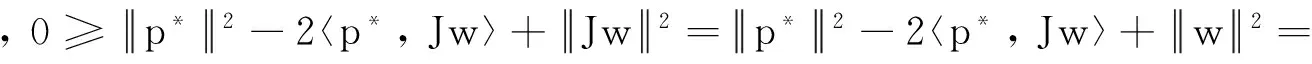
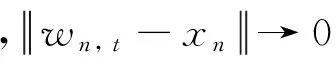
如果τ*∈Tτ， 根據算子T的單調性可得: 〈τ-Jλnwn, t, τ*-Aλnwn, t〉≥0(?n≥0， t≥0 ).

令n→∞， 得到〈τ-p*, τ*〉≥0， 因此， 由T的極大單調性可得: p*∈T-10.

最后， 由{xn}有界和Γ:={T(t):t≥0}為({νn}、 {μn}、 ζ)全局擬-φ-漸近非擴張半群， 可證明p*∈F(Γ)且p*=ΠΞx0. 定理1證畢.

由定理1可得如下的定理2和定理3， 證明省略.

定理2 設E、 C、 {αn}、 {βn}、 {λn}都如定理1所定義. 設A: C→E*為α-逆強單調算子， 二元函數Φ:C×C→R滿足條件(A1)～(A4). 設極大單調算子T:E→2E*滿足Jλ：=(J+λT)-1J, ?λ>0.Γ:={T(t):t≥0}為閉的、 一致Lipschitz和({kn})擬-φ-漸近非擴張半群(其中{kn}?[1, ∞)，kn→1且滿足Ξ≠?). 若Ξ在C中有界， 那么由算法1產生的序列{xn}強收斂于ΠΞ(x0).

定理3 設E、C、 {αn}、 {βn}、 {λn}都如定理1所定義； 設A:C→E*為α-逆強單調算子， 二元函數Φ:C×C→R, 滿足條件(A1)～(A4). 設極大單調算子T:E→2E*滿足Jλ：=(J+λT)-1J, ?λ>0.Γ:={T(t):t≥0}為閉的、 ({kn})擬-φ-漸近非擴張半群(其中{kn}?[1, ∞)，kn→1且滿足Ξ≠?；ΠCn+1:E→Cn+1為廣義投影). 則由算法1生成的序列{xn}強收斂于ΠΞ(x0).

[1]TakahashiS,TakahashiW.StrongconvergencetheoremforageneralizedequilibriumproblemandanonexpansivemappinginHilbertspace[J].NonlinearAnalysis, 2008, 69: 1 025-1 033.

[2]CombettesPL,HirstoagaSA.EquilibriumprogramminginHilbertspaces[J].JournalofNonlinear&ConvexAnalysis， 2005, 6(1): 117-136.

[3]TakahashiS,TakahashiW.ViscosityapproximationmethodsforequilibriumproblemsandfixedpointproblemsinHilbertspaces[J].JournalofMathematicalAnalysis&Applications, 2007, 331(1): 506-515.

[4]ChangShin-sen,LeeHWJ,ChanChi-kin.AnewhybridmethodforsolvingageneralizedequilibriumproblemsolvingavariationalinequalityproblemandobtainingcommonfixedpointsinBanachspaceswithapplications[J].NonlinearAnalysis:Theory,Method&Applications, 2010, 73(7)： 2 260-2 270.

[5]CengLuchuan,GuuSy-ming,HuHY,etal. Hybrid shrinking projection method for a generalized equilibrium problem, a maximal monotone operater and a countable family of relatively nonexpansive mappings[J]. Computers and Mathematics with Applicaions, 2011, 61(9): 2 468-2 479.

[6] Chang Shih-sen, Kim J K, Wang Lin. Total quasi-φ-asymptotically nonexpansive semigroups and strong convergence theorems in Banach spaces[J] . Fixed Point Theory and Applications, 2012(1): 1-14.

[7] Kamimura S, Takahashi W.Strong convergence of a proximal-type algorithm in a Banach space[J] . Society for Industrial and Applied Mathematics Journal on Optimization, 2002, 13(3): 938-945.

[8] Saewan S, Kumam P. The shrinking projection method for solving generalized equilibrium problems and common fixed points for asymptotically quasi-φ-nonexpansive mappings[J]. Fixed Point Theory and Applications, 2011(1): 8-11.

[9] Rockafellar R T. On the maximality of sums of nonlinear monotone operators[J]. Transactions of the American Mathematical Society, 1970, 149(1): 75-88.

[10] Kohsaka F, Takahashi W. Strong convergence of an iterative sequence for maximal monotone operators in a Banach space[J]. Abstract and Applied Analysis, 2004(3)： 239-249.

(責任編輯： 林曉)

Strong convergence theorems of an iterative method for a generalized equilibrium problem, a maximal monotone operator and total quasi-φ-asymptotically nonexpansive semigroups

WU Yanlin

(Department of Basic Teaching, Yango College, Fuzhou, Fujian 350015, China)

We propose an iterative scheme for finding a common element of the solutions of a generalized equilibrium problem, a maximal monotone operator and total quasi-φ-asymptotically nonexpansive semigroups. Under some appropriate conditions, we establish some strong convergence theorems of the sequences generated by our proposed scheme.

maximal monotone operator; total quasi-φ-asymptotically nonexpansive semigroups; generalized equilibrium problem; common fixed point

2014-09-07

吳燕林(1984-)， 講師， 主要從事非線性優化研究，wyl-kk@163.com

福建省自然科學基金資助項目(2014J01008)

10.7631/issn.1000-2243.2015.06.0733

1000-2243(2015)06-0733-05

O122.3

A