不同系統接線方式下電壓調差率的 整定計算

陳延云 蔡 培 王 銳 戴申華

（1. 國電科學技術研究院，南京 210031； 2. 陸軍軍官學院，合肥 230031；3. 安徽省電力科學研究院，合肥 230601）

并列運行的同步發電機組通常借助于電壓調差率來實現無功功率穩定合理的分配。發電機的電壓調差率包括自然調差率和附加調差率。自然調差率又稱靜差率，現代勵磁控制系統穩態增益很大，等于或近似于無差調節，其自然調差率很小，僅靠自然調差率是不能滿足機組無功功率分配要求的。為保障機組和電網的安全經濟運行，通常需要配置合適的附加調差[1]。若勵磁系統調差系數過大，當發電機追蹤負荷無功變化時，電網運行電壓波動較大，從而影響電壓質量，增加電網網絡損耗和運行風險；若勵磁系統調差系數過小，當電網運行電壓微小的變化時，發電機輸出更多的無功功率，同時對于并聯運行的發電機組將會發生搶無功現象，不利于發電機安全運行[2]。

目前，對于電壓調差率整定的基本原則、極性選擇方面已有不少文獻作過討論[3-5]。對于機端直接并聯運行的發電機組，為了使無功電流能夠穩定分配，需要一定的正調差，附加調差系數應為正。當兩臺及以上發變組單元在高壓側母線并列時，為了機組能夠穩定運行，要求各個機組在并列點的調差系數為正調差。對于在高壓側并聯的發電機變壓器組，由于升壓變壓器電抗大，發電機無功負荷增大時，高壓母線電壓下降過多，不利于穩定運行，需要采用負的附加調差系數以補償變壓器電抗。

筆者曾對國內各區域電網大型發電機組勵磁系統調差系數的整定現狀進行深入調研，發現調差系數的整定工作存在很大的隨意性，區域差異較大，定值整定范圍寬、管理不規范等問題較突出，有些機組甚至不投入附加調差環節，極大的影響了機組的無功調節能力。為此，對常見系統接線方式下的調差率整定計算進行分析研究，為發電廠提供具有實用價值的整定計算方法，對機組和電網的安全經濟運行具有重要意義。

1 發電機-變壓器單元接線

目前，大型發電機組一般采用發電機-變壓器單元接線方式，通過主變高壓側母線并列，并列點處的調差系數決定了各機組之間的無功分配關系和并列點處電壓。這種接線方式中，由于變壓器電抗大，發電機無功負荷增大時，高壓母線電壓下降過多，不利于穩定運行，需采用負的附加調差系數以補償變壓器電抗，加快高壓母線的電壓響應速度，提高系統電壓穩定性。

1.1 整定計算

主變短路阻抗以主變容量為基值，勵磁附加調差以發電機額定容量為基值，兩者需轉換到同一電壓等級下的有名值進行計算。主變短路阻抗有名值發電機附加調差有名值為兩者相加后得到并列機組在有功電流為零時電壓調差率的有名值：

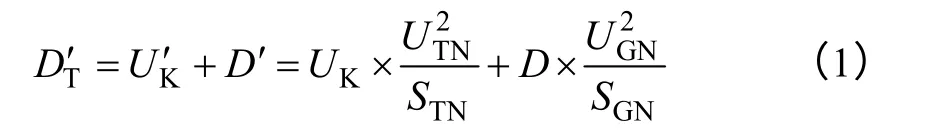
將式（2）化簡得到

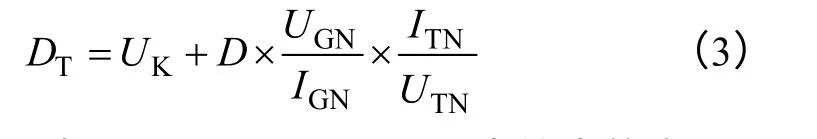
式（3）就是標準DL/T 843—2010 中給出的電壓調差率整定計算公式[6]。

1.2 算例

某火力發電廠總裝機容量為2×125MW，發電機通過主變壓器接入220kV系統。機組參數如表1所示。

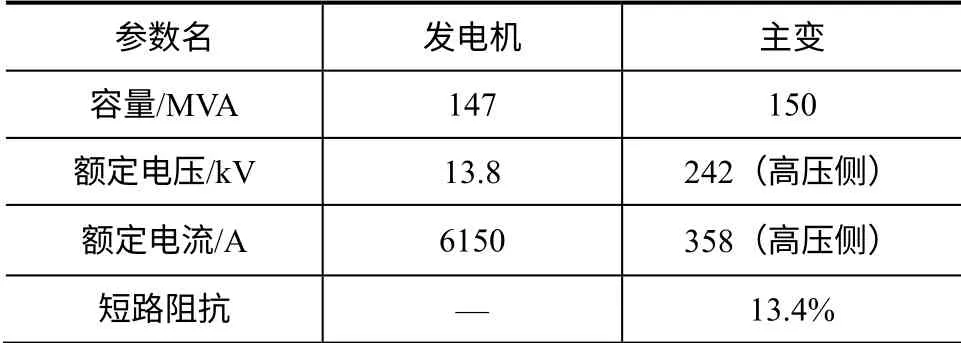
表1 機組參數

設定DT= 5%，根據式（3），計算得到調差率為-8.57%（以發電機額定容量為基值），結果符合工程應用需求。

特別值得一提的是，對于式（3），計算主變壓器高壓側并列發電機變壓器組的調差率，涉及到主變壓器的額定電壓和額定電流。主變壓器和發電機用同一電壓側的電壓和電流，即：主變壓器用低壓側的額定電壓和電流時，發電機也用同一低壓側的額定電壓和電流，主變壓器用高壓側的額定電壓和電流時，發電機的額定電壓和電流應折算到高壓側。

2 經三繞組變壓器并列接線

相對于發電機-變壓器組單元接線方式，經三繞組變壓器并列的接線方式較復雜，調差率設置考慮因素較多。圖1中，兩臺發電機通過兩臺三繞組變壓器分別在高、中壓側并聯，高壓側接入電網，中壓側母線為本地負荷母線，無功需求較大。建立該并聯方式的等效電路，如圖2所示。

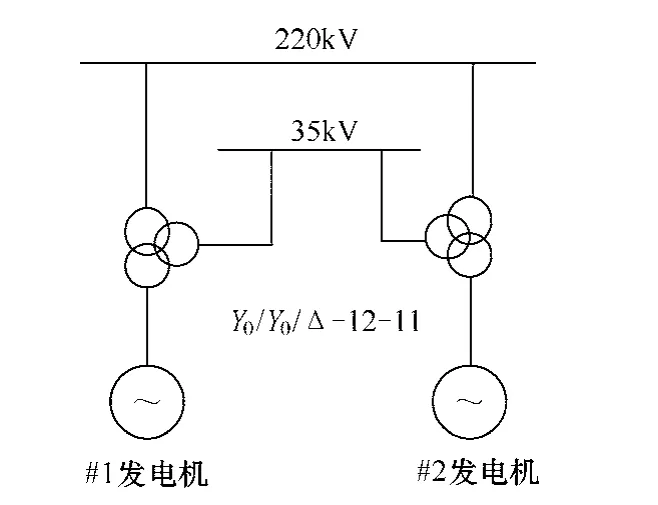
圖1 發電機經過三繞組變壓器并列運行

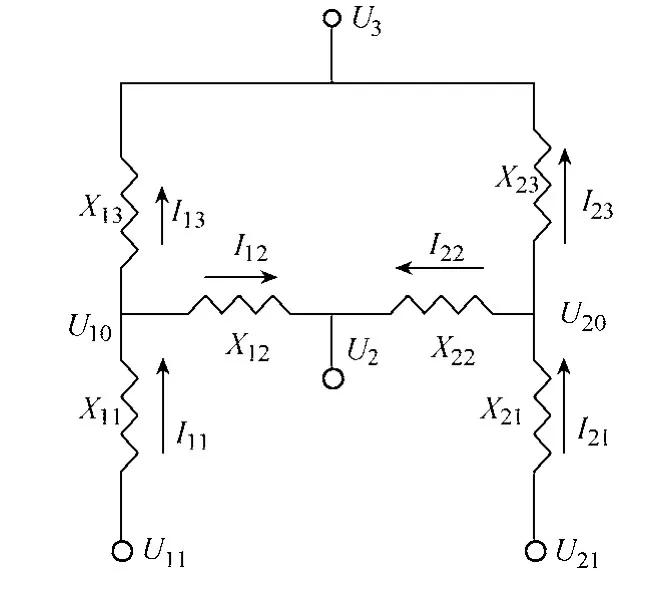
圖2 等效電路

U11、U21分別為發電機機端電壓，U2、U3分別為35kV 和220kV 母線電壓，I11、I12、I13、I21、I22、I23分別為發電機和變壓器的無功電流。由于變壓器的兩端電壓相角差和電阻很小，所以變壓器的電壓損耗近似用無功電流在阻抗上的電壓降來代替。

根據圖2，有以下四個公式成立：

聯立式（5）至式（7），消去I12、I13，可得出U10的計算公式：

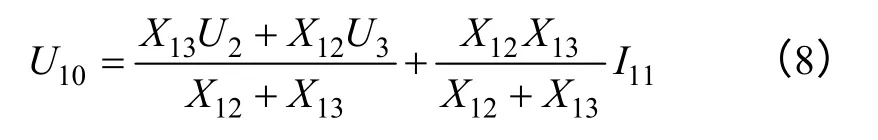
由式（4）和式（8），可得#1 發電機機端電壓：

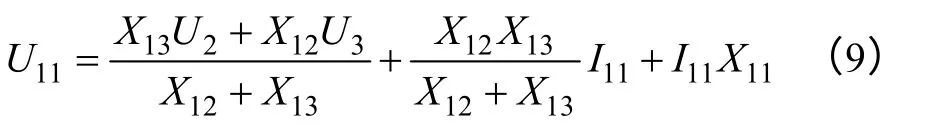
設#1 機組調差系數為XC1，#2 機組調差系數為XC2，Uref1為勵磁調節器給定值，綜合考慮調差環節的影響，可得#1 發電機勵磁系統輸出偏差為

若此時勵磁調節器穩態增益為KA，則由式（10），可得出勵磁調節器輸出的勵磁電壓EFD1為

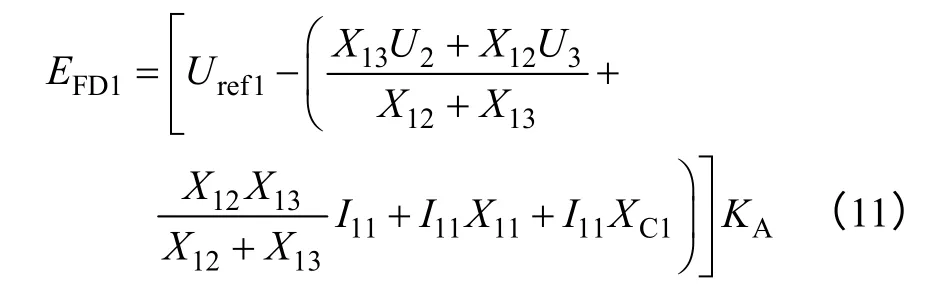
同理，可得到#2 發電機勵磁調節器輸出的勵磁電壓EFD2為

2.1 調差率設置對無功平衡影響分析

取中間量X′1、X′2：

1）設置方式一：XC1＜X1′，且XC2＜X2′

此時在#1 發電機和#2 發電機之間產生一個環流ΔI，從式（11）可見，EFD1有一個正的增量，同時，EFD2有一個負的增量，而EFD1的增大和EFD2的減小將導致ΔI繼續增大，最終出現#2 發電機深度進相，#1 發電機不斷發無功的不穩定現象，直至#2發電機低勵限制動作或#1 發電機過勵限制動作。所以，這種設置是不允許的。

2）設置方式二：XC1＞X1′，且XC2＜X2′，或XC1＜X1′，且XC2＞X2′

這里我們以XC1＞X1′，且XC2＜X2′為例來分析該調差設置的最終結果。如果此時因為某種原因在#1 發電機和#2 發電機之間產生環流ΔI，從公式（11）可見，EFD1有一個負的增量，同時，EFD2也有一個負的增量，兩臺發電機都在降低電壓，這樣的結果就是母線電壓迅速下降，影響系統穩定運行。所以，這種設置也是不允許的。

3）設置方式三：XC1＞X1′，且XC2＞X2′

如果此時在#1 發電機和#2 發電機之間產生一個環流ΔI，從公式（11）可見，EFD1有一個負的增量，同時，EFD2有一個正的增量，而EFD1減小和EFD2增大導致ΔI減小，這個環流越來越小，最終兩臺機組通過平衡無功分配直至穩定，設置合理。

4）整定計算

設期望得到并列點的調差率為X，則XC1、XC2的計算公式為（計算過程應將阻抗值折算到同一個標幺系統下）：

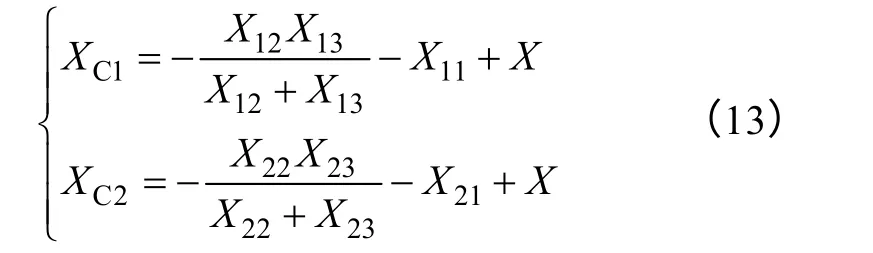
如果XC1和XC2設置過大，則勵磁電壓對無功變化將十分敏感。工程實踐和相關分析計算推薦電壓調差率整定為3%～5%（以發電機額定無功功率為基值）。

2.2 算例

某熱電廠有兩臺機組通過三繞組變壓器并列運行，機組容量63MVA，主變容量63MVA，調差系數初始整定值#1 機組為-3%，#2 機組為-4%。當兩臺機組并列運行時2 號發電機低勵限制動作，1 號發電機無功出力增大，無功分配不穩定。

表2 主變壓器短路電抗

根據機組參數可計算得到：

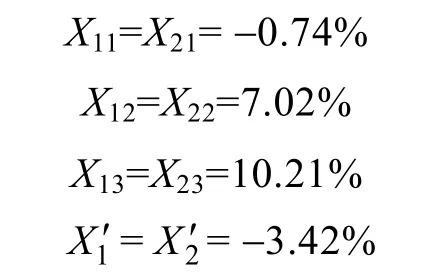
顯然屬于前文分析的調差設置類型之中的第二種（XC1＞1X′，且XC2＜2X′），是一種不正確的設置，所以出現了搶無功現象。

為了避免出現搶無功現象，將兩臺機組的調差系數設置為零，則其等效調差為3.42%，為正調差，更改調差整定值后，機組并列運行時無功調節正常，調差設置正確。

3 結論

并列運行的發電機組，并列點的電壓調差率整定需綜合考慮發電機的自然調差、附加調差和主變壓器壓降等因素。對于發電機-變壓器單元接線方式，標準DL/T 843—2010 中給出的整定計算公式具有很好的工程實用價值，但計算時主變壓器和發電機參數必須采用同一電壓側的電壓和電流。經三繞組變壓器并列的接線方式，調差率設置不能簡單的補償變壓器阻抗，要充分考慮高、中壓側的協調問題。本文針對上述兩種系統接線方式提出了整定計算方法，并通過實際應用驗證了方法的有效性，希望能為類似接線的機組提供參考。

[1] 竺士章. 發電機勵磁系統試驗[M]. 北京: 中國電力出版社,2005.

[2] 劉取. 電力系統穩定性及發電機勵磁控制[M]. 北京:中國電力出版社,2007.

[3] 方思立,蘇為民. 大型發電機調差率整定及調試[J].中國電力,2006,39(8): 12-15.

[4] 張寧,李海翔. 同步發電機組電壓調差系數實用整定方法研究[J]. 浙江電力,1996,15(5): 6-9.

[5] 陳繼武. 勵磁調節器中的調差問題[J]. 華東電力,2002,(10): 35-36.

[6] DL/T 843—2010 大型汽輪發電機勵磁系統技術條件[S].

[7] 郭玉恒,徐學琴. 機組并網瞬間搶無功現象分析及定值整定策略[J]. 水電自動化與大壩監測,2011,35(3): 21-24.