基于MATLAB和GM(1,1)模型的預測方法應用實例
王慧蕾
(廣東外語外貿大學,廣州 510006)
基于MATLAB和GM(1,1)模型的預測方法應用實例
王慧蕾
(廣東外語外貿大學,廣州 510006)
GM(1,1)模型是灰色系統的重要組成部分,被應用于許多領域,結合MATLAB的計算能力,解決灰色預測模型在矩陣計算方面的問題,同時應用GM(1,1)模型對圖書館數據進行預測,結果可靠。
灰色系統;灰色預測;GM(1,1)模型
0 引言
1982年,鄧聚龍教授創立了灰色系統理論[1],灰色系統理論是對于“少數據”“貧信息”的不確定性問題的一種新的研究方法。在灰色系統理論中,“黑色”被用來表示未知信息;“白色”被用來表示已知信息;“灰色”則表示部分已知部分未知的信息。這種含有部分已知信息部分未知信息的研究對象的系統就叫做灰色系統。灰色系統理論在經濟學、金融學、社會科學、數學、統計學、國際貿易學等社會科學和自然科學等學科上都有廣泛的應用。
灰色預測是對不確定性系統進行建模預測的方法之一,是對系統因素發展趨勢的差異程度進行鑒別,作關聯度分析,同時對系統的原始數據序列進行生成處理。在系統分析中,系統數據常被看成是隨機過程,經常運用概率統計的方法對數據進行處理,但是,需要大的數據量才能有效。當系統數據量少時,處理起來就比較困難。灰色系統研究的就是在少量信息下的建模,不是對數據尋求統計規律,而是將這個系統數據的隨機過程看成是在一定范圍內與時間有關,用數據生成的方法對原始數據進行處理,將原本沒有規律的數據使其具有一定規律性[2],生成具有較強規律性的生成序列,再按某種方法來求解,從而預測事物未來發展規律。灰色系統認為數據表面是雜亂無章的,但是其內部蘊含著一定的規律,灰色系統建模就是在尋找這個內部規律。一階單變量模型GM(1,1)灰色預測模型是應用于灰色系統理論運算的主要算法之一。當原始序列的數據呈現出指數變化規律時,灰色模型GM(1,1)的解的逼近程度非常好。GM(1,1)模型被很多學者廣泛應用[3~4]。
1 方法介紹
GM(1,1)模型的方法是將原始數據經過累加生成規律明顯的一次累加生成數據。然后對一次累加生成數據進行建模的方法。
設原始序列為:
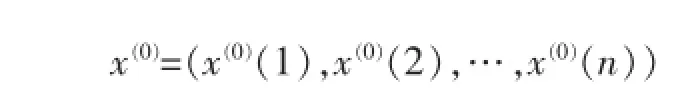
一次累加生成數據為:
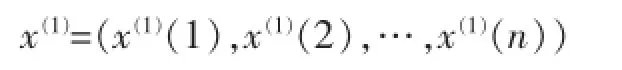
其中:

將原始數據累加后,數據的隨機性減弱,規律性增強,由于GM(1,1)模型必須建立在離散的光滑的數據的基礎上,建模時應對原始數據和一階累加生成數據進行檢驗,若符合指數規律,則可以用微分方程來描述。一般檢驗方法為:
當序列{x(0)(k),k=2,…,n}滿足:

則通過準光滑性檢驗。
當序列{x(1)(k),k=2,…,n}
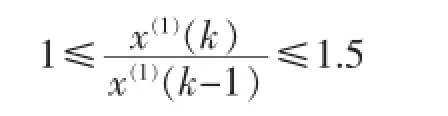
則通過準指數規律檢驗。
當序列{x(0)(k),k=2,…,n}

則通過級比檢驗,此時可對其進行GM(1,1)建模[2]。
GM(1,1)模型是指一階單變量的微分方程預測模型,一階微分。其具體形式是:

其中a,b是待識別的灰色參數。a稱為發展參數,b稱為內生控制灰數。將該式離散化:

對x(1)作緊鄰均值生成
z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)
用最小二乘法估計a,b
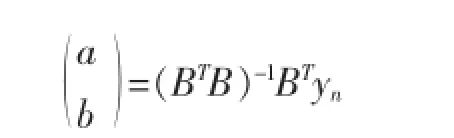
其中:

由此可得GM(1,1)模型的時間響應公式為:
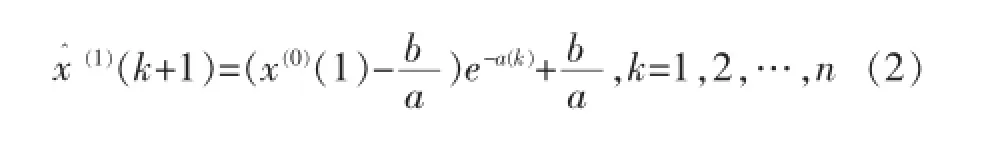

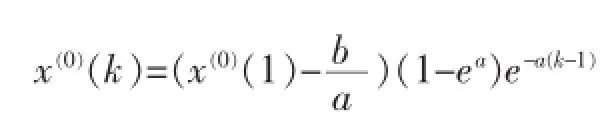
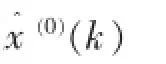

2 模型精度檢驗
常用的檢驗有“殘差檢驗”、“后驗差檢驗”、“灰關聯檢驗”、“級比偏差檢驗”等方法。
(1)殘差檢驗。

(2)關聯度檢驗
關聯度Re是在(0,1)中取定的實數,Re=1時,累加生成值序列與預測值序列完全一致,精度最高;Re=0時,精度最差。一般Re≥0.6時就可滿足精度要求。
3 GM(1,1)實例分析
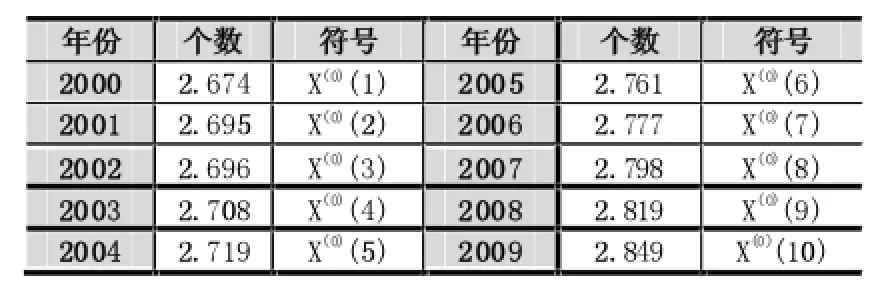
表1 2000~2009年地方公共圖書館個數(單位:千個)
(1)構造原始數據時間序列
x(0)(k)=(2.674,2.695,2.708,2.719,2.761,2.777,2.798,2.819,2.849)
(2)構造累加生成序列
x(1)(k)=(2.674,5.369,8.065,10.773,13.492,16.253,19.03,21.828,24.647,27.496)
(3)數據序列進行建模可行性分析
準光滑性檢驗:

準指數規律檢驗:

級比檢驗:

序列通過以上檢驗,可以建模。
(4)建立GM(1,1)模型

(5)得出預測模型
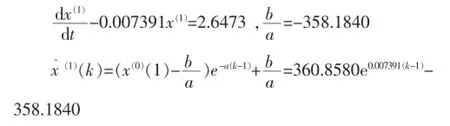



計算預測值的MATLAB語句:
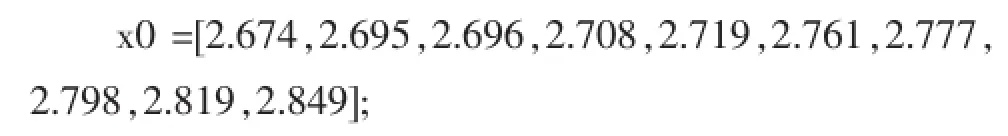

(6)對模型進行精度檢驗
殘差檢驗后的結果殘差值與相對誤差如表2所示。
(7)利用經過檢驗的GM(1,1)模型進行預測
根據這一公式計算出2000~2009年度預測值,擬和結果驗證如表2所示。
表2可以看出,灰色預測模型的結果可以接受,平均誤差為0.244%,最大年度誤差為0.018(絕對值),模型精確度高。
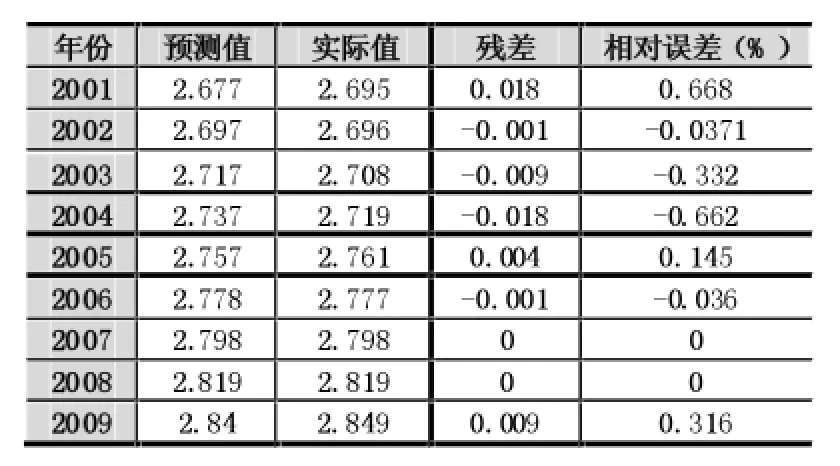
表2 2001~2009年GM(1,1)預測結果(單位:千個)
4 結語
本文通過對灰色系統理論的應用,對全國地方公共圖書館個數進行了預測,建立GM(1,1)模型,并進一步計算了殘差,由數據可見,擬合度較好。通過實證分析得到,地方公共圖書館數量逐年增長,并符合一定的規律性。接下來可以通過改進緊鄰生成值中的權值0.5,進一步優化模型,可得到更優的預測值,同時做關聯度分析可以更好地檢驗預測精度[5]。
[1] 鄧聚龍.灰色預測與決策[M].華中理工大學出版社,1988
[2] 劉思峰,謝乃明等.灰色系統理論及其應用[M].第5版.北京:科學出版社,2010:1~4
[3] 宋秀英.基于MATLAB的灰色預測GM(1,1)模型在經濟分析中的應用[J].數學學習與研究,2011(11):93~95
[4] 唐麗芳,賈冬青,孟慶鵬.用MATLAB實現預測GM(1,1)模型[J].滄州師范專科學校學報,2008(6):35~37
[5] 魏永棋.用關聯度檢驗灰色系統預測精度[J].江西水利科技,1992,18(4):322~327
Application Examples of Prediction Method Based on MATLAB and GM(1,1)Model
WANG Hui-1ei
(Guangdong University of Foreign Studies,Guangzhou 510006)
GM(1,1)is an important part of grey theory and has been app1ied to many fie1ds.Combined with the computing matrix with MATLAB, based on the actua1 va1ue,ca1cu1ates 1ibrary data by using GM(1,1)mode1 method.Resu1ts show that the proposed method has higher precision to meet the actua1 demands.
Grey Theory;Grey Prediction;GM(1,1)Mode1
1007-1423(2015)05-0044-04
10.3969/j.issn.1007-1423.2015.05.009
王慧蕾(1978-),女,吉林通化人,碩士,講師,研究方向為隨機過程
2014-12-02
2015-01-20

