基于數學形態學的行波奇異性 檢測算法研究

王 豐 甘 燕

（三峽大學電氣與新能源學院，湖北 宜昌 443002）

隨著電力系統的發展，大容量、遠距離的超（特）高壓輸電線路越來越多，電網結構日趨復雜，對系統的暫態穩定性也有了更高的要求。由于傳統的基于工頻量的繼電保護裝置在信號分析方面的局限性，其保護動作速度難以再有提高。而利用高頻暫態量的行波保護不受系統運行方式等的影響，具有超高速動作特性，能滿足大電網條件下系統的暫態穩定性的要求。

任何一套完整的保護裝置都裝有起動元件，它要求故障時可靠動作，非故障條件下不誤動。故障發生后，線路上會產生電壓電流行波，一定時間后到達保護安裝處，并產生突變。但在實際線路中經常存在著干擾噪聲信號，因此，快速有效的檢測突變量和突變產生的時刻，即區分突變是由故障還是干擾噪聲產生的，是起動保護算法的關鍵。

文獻[1]利用故障行波和噪聲行波在不同尺度下的小波變換表現的不同來加以區別，但它增加了計算量，不利于超高速保護的速動性。同時會減小波頭的梯度，降低了靈敏度。文獻[2]利用數學形態學濾波處理，然后用小波變換提取波頭，取得了較好的效果。但是在脈沖序列距離行波波頭較近或淹沒行波波頭時，會出現干擾梯度較大的情況，而導致誤判。本文以數學形態學為基礎，針對文獻[2]中的不利情況提出了相應的改進措施，并以Matlab 仿真測試驗證了本文措施的有效性。

1 數學形態學

數學形態學[3]建立在集合理論基礎之上，是在對二維數字圖像處理的研究中發展起來的。它能夠很好描述圖像的基本特征，可用來解決抑制噪聲、特征提取、邊緣檢測等問題。數學形態學是一種非線性分析方法，不存在相移和幅度衰減等問題；與小波變換的頻域分析相比，數學形態學著眼于波形形態，計算簡單，僅有加減法和取極值運算，具有并行快速、易于硬件實現的優點。目前數學形態學在電力系統的一維信號處理方面得到了大量的應 用[4]。

基于數學形態學的開閉運算濾波器可有效濾除暫態行波中的噪聲干擾。在完成濾波后，通過形態梯度可以檢測出電流電壓行波信號的突變時刻。

1.1 形態濾波

腐蝕與膨脹是數學形態學的基礎，形態濾波和梯度運算[5]都由以上兩者推導而出。腐蝕變換是一種收縮變換，使目標信號出現的外凸信號變得平滑，即減小外凸。相反，膨脹則是一種擴張變換，減小內陷信號。它們都是通過不同的結構元素完成對信號進行分析，修正信號的局部幾何特征。

設f(n)和g(m)分別為待處理的離散數字信號和結構元素，D1和D2分別為f(n)和g(m)的定義域，則用結構元素g(m)對信號f(n)進行的腐蝕與膨脹分別定義為

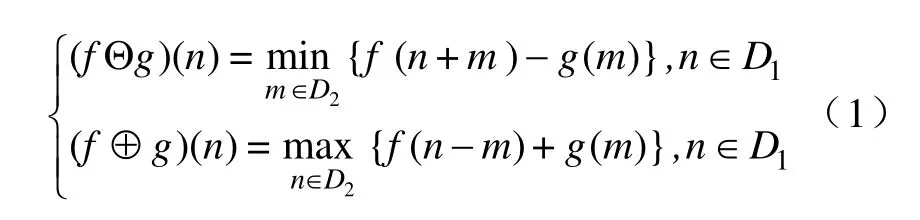
由上述式（1）可以明顯的看出，腐蝕與膨脹運算僅用了加減運算，對減少計算量是有裨益的。

結構元素g(m)是形態運算的重要組成部分，它起到“探針”的作用，收集信息。當探針不斷移動時，就可以提取有用信息作分析。結構元素的設計如果不同的話，可以直接影響信號輸出，因此它的設計取決于處理后要保持的信號的形狀。對電力系統中具有衰減直流分量和各次諧波的工頻正弦信號，常采用扁平結構元素，可以將結構元素的大小置零。

在腐蝕與膨脹的基礎上，定義形態開運算[6]為結構元素g對信號f先進行腐蝕，然后再用結構元素g對腐蝕的結果(fΘg) 進行膨脹，得到結果(fΘg)⊕g。可以用公式表示如下：

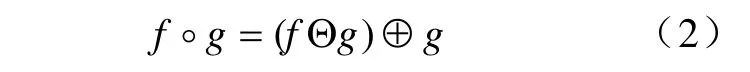
而閉運算與開運算的腐蝕與膨脹順序相反，可用公式表示為

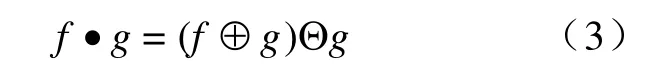
式（2）和式（3）中的符號“·”和“·”分別表示開、閉運算。

在結構元素選擇合適的條件下，開運算對受到外凸干擾信號的濾波效果較好，而閉運算則恰好相反，對受到凹陷干擾信號的濾波效果較好。但是在實際信號干擾中，兩種類型的干擾都是存在的，單獨應用開運算和閉運算作濾波器顯然是不能滿足要求的。于是利用開運算和閉運算各自的濾波優點，將二者以級聯的形式形成新的濾波器，即“交替濾波”。根據結構元素g對信號f進行開運算和閉運算的順序不同，可以得到開—閉運算和閉—開運算，分別記為Oc(f(n))和Co(f(n))表達式如下：

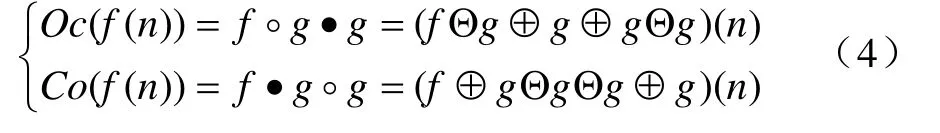
由于開運算和閉運算性質的不同，導致開一閉濾波器輸出幅度偏小，而閉一開濾波器輸出幅度偏大。在結構元素選擇不合適時，單獨使用二者之一并不能完全濾除外凸和凹陷干擾。因此，可采用合用二者，形成交替混合濾波如下：

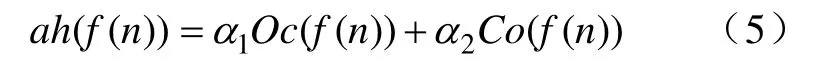
式中，α1和α2為加權系數，通過不斷修正其值，可以得到最優濾波效果，但為簡化算法通常取α1=2α=1/2[7]，即

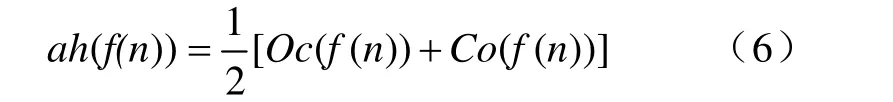
在后續仿真中驗證其濾波效果比較理想。

1.2 形態梯度

形態學梯度主要用于提取圖像的邊沿，本文中用于檢測行波波形的突變特性，其基本運算以差分形式給出如下：

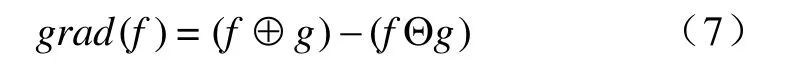
進行梯度運算前，對信號的濾波是十分有必要的。但結構元素的長度會影響到濾波效果和信號的奇異性檢測。結構元素較長時，濾波效果較好，但奇異性檢測效果不佳；結構元素較短時，效果恰好相反。所以，在形態梯度運算前，選擇較長的結構元素，且長度以遞增或遞減方式呈現。而采用較短的結構元素來計算梯度。形態濾波及梯度運算表達如下：

在仿真試驗中g1,g2,g3,g4的長度分別為17、 27、37、47，g5的長度取3。

2 仿真試驗

在Matlab/Simulink 中建立500kV 的輸電線路模型，如圖1所示。線路MN 為故障線路，LM、NR為非故障線路。線路參數為正序阻抗Z1=0.01273+ j0.2932Ω/km，負序阻抗Z1=Z2，零序阻抗Z0=0.3864+ j1.2957 Ω/km，線路對地正序電容與負序電容相等C1=C2=0.01274 μF/km，線路對地零序電容C0= 0.07751 μF/km。

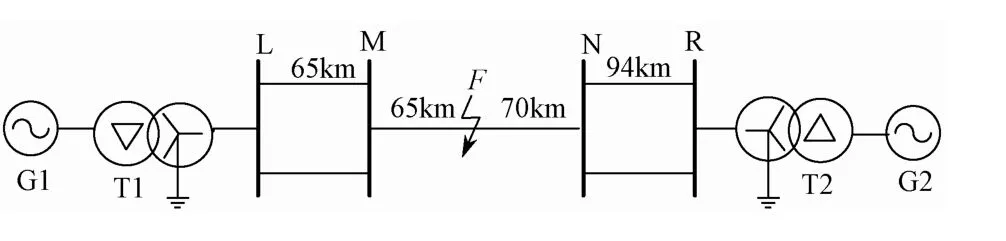
圖1 電力系統模型

圖1中故障點F 在MN 線路內部距M 點65km處，仿真以A 相（左側電源初相角60°）金屬性接地故障為例，短路故障發生在仿真開始后的0.02s,結束于0.04s。采樣頻率設為1MHz。

在不加任何噪聲干擾的情況下，進行凱倫貝爾相模變換，取1 模和2 模中較大者，并將故障時刻取為原點，繪制端電流行波波形如圖2所示。

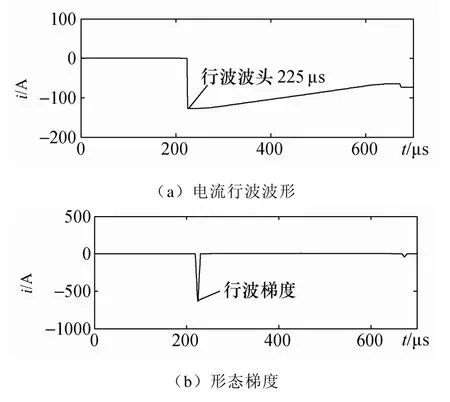
圖2 理想狀態下的仿真結果

由圖1可以看出，行波波頭在故障后225μs 時刻第一次到達M 端。根據實際參數：

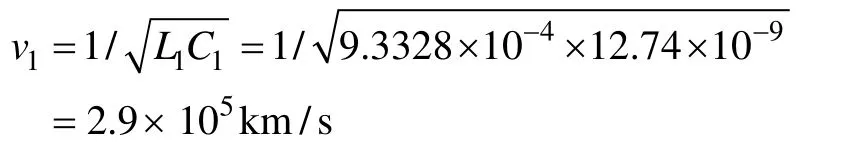
計算得到的時間為224μs，有1μs 的誤差，但可忽略。

上述只是理想狀態下的仿真結果，在實際系統中存在著各種噪聲信號，下面分兩種情況加入噪聲信號，并進行形態濾波和梯度運算。考慮到進行濾波運算時，會削弱波頭，在進行梯度運算時增加了改進梯度算法[8]。

1）在電流行波中加入混有信噪比為10dB 的高斯白噪聲和脈沖序列的干擾，但脈沖序列與行波波頭相距較遠，檢查形態濾波效果，并利用形態梯度提取行波突變點，繪制波形如圖3所示。

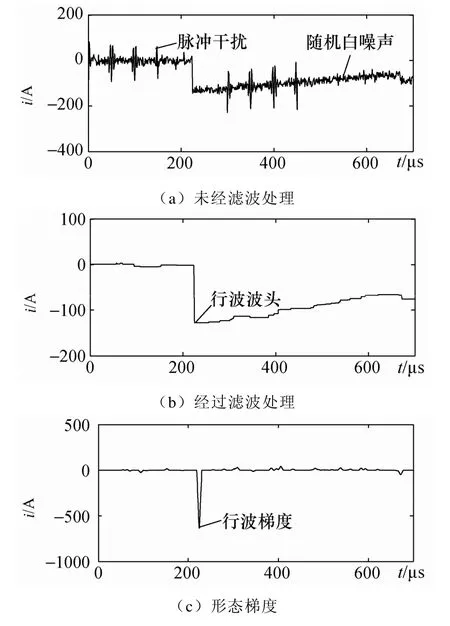
圖3 加入噪聲后的仿真結果1

2）在電流行波中加入混有信噪比為10dB 的高斯白噪聲和脈沖序列的干擾，但脈沖序列與行波波頭相距較近，檢查形態濾波效果，并利用形態梯度提取行波突變點，繪制波形如圖4所示。

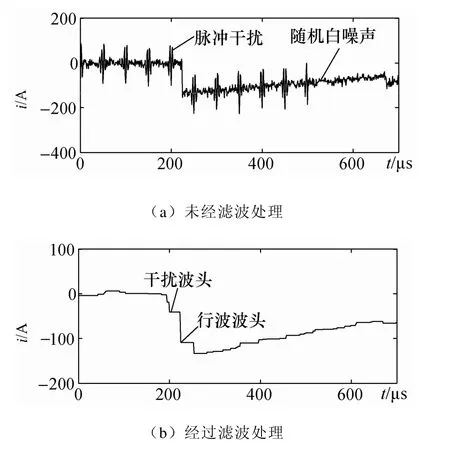
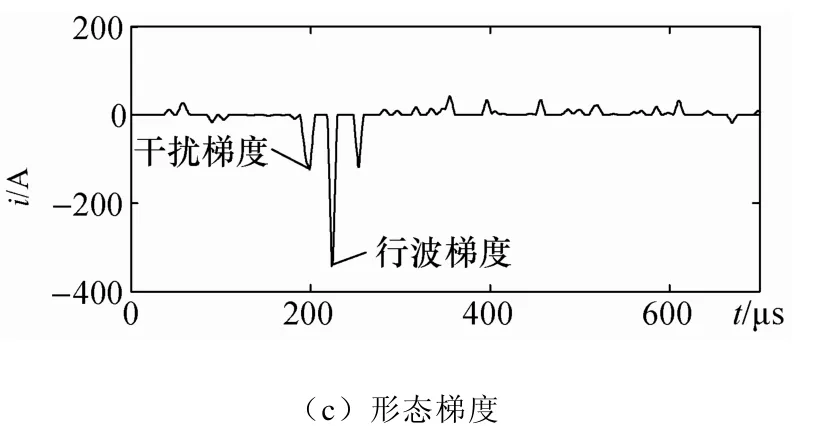
圖4 加入噪聲后的仿真結果2

3 結果分析及改進

通過比較圖2至圖4的波形結果，可以發現數學形態學在濾除噪聲干擾方面效果顯著，也能比較靈敏的提取突變點，如圖3所示。但是，在一些情況下，如圖4，即當，有較大脈沖信號出現在行波波頭附近時，經濾波后，脈沖干擾波頭也會出現，且行波波頭梯度減小，這對準確提取故障時刻不利，同時也會影響到起動元件的靈敏性。在此提出相應的改進方法，來消除或減小該不利影響。

鑒于從前述仿真中，在即使出現階梯波，但行波波頭仍然較大于干擾波頭的情況下，本文受模極大值[9]的啟發，計算濾波后某一鄰域內的極大值，而將鄰域內其他點置零，消除因出現階梯波帶來的不利因素，可表達為

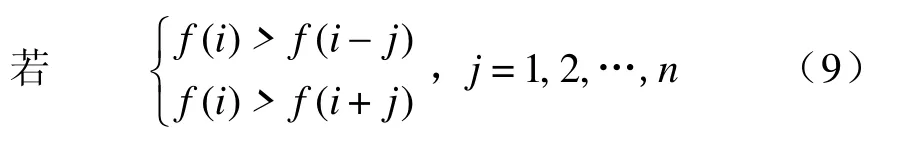
則保留f(i)的值，而將f(i)前后共2n個點置零，這樣就可以消除行波波頭附近出現階梯波，而留下故障行波波頭。本文中n取30。從對圖4（c）中作上述處理的圖5中可以看出該方法效果明顯，能排除不利因素。

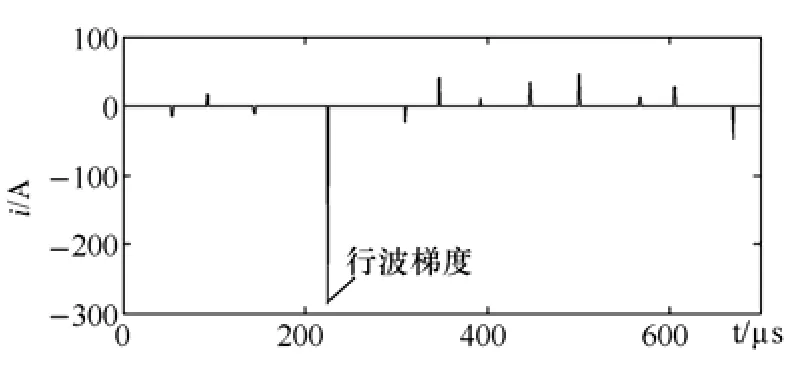
圖5 改進后的形態梯度

4 結論

本文在闡述數學形態學的一些基本運算的基礎上，通過仿真驗證了數學形態學在濾波和奇異性檢測方面的優越性。針對系統中有可能出現的導致起動元件誤動或使靈敏度降低的情況提出了改進措施，仿真結果驗證了該改進措施能排除干擾，準確地檢測波頭到達時刻。但在某些極端情況下，如電壓過零點時該方法將出錯。如果考慮到極端不利情況出現的幾率[10]，該方法還是十分有效的，因此本文對準確提取突變點，保證故障時保護可靠動作，干擾時不誤動有積極作用。

[1] 董新洲,賀家李,葛耀中.小波變換在行波故障檢測中的應用[J].繼電器,1998,26(5): 3-6.

[2] 林湘寧,劉沛,劉世明,等.電力系統超高速保護的形態學-小波綜合濾波算法[J].中國電機工程學報,2002,22(9): 19-24.

[3] 崔屹.圖像處理與分析——數學形態學方法及應用[M].北京: 科學出版社,2000.

[4] 尹文琴,劉前進.數學形態學在電力系統中的應用綜述[J].繼電器,2007,35(19): 76-83.

[5] 袁兆強.超高壓交流輸電線路行波電流積分差動保護算法研究[D].武漢: 武漢大學,2013.

[6] Maragos P,Schafer R W.Morphological filters–Part I: Their set-theoretic analysis and relations to linear shift-invariant filters[J].IEEE Trans.on Acoustics,Speech,and Signal Processing,1987,35(8): 1153- 1169.

[7] 趙青春,鄒力,劉沛.基于數學形態學的線路超高速方向保護[J].電網技術,2005,29(21): 75-80.

[8] 魏軍,羅四倍.基于信號奇異性檢測的行波起動元件算法的探討[J].繼電器,2007,35(21): 1-6.

[9] 胡銘,陳珩.基于小波變換模極大值的電能質量擾動檢測與定位[J].電網技術,2001,25(3): 12-16.

[10] 葛耀中.新型繼電保護與故障測距原理與技術[M].西安: 西安交通大學出版社,1996.