交直流電力系統暫態過程中同步發電機 阻尼轉矩系數的計算
吳學蘋 江寧強
(南京理工大學自動化學院電氣工程系,南京 210094)
同步發電機的阻尼轉矩系數對電力系統的暫態穩定性有重要影響。多擺失穩與阻尼轉矩的聯系在穩定研究中已引起關注。利用BCU 法(Boundary of stability region based on Controlling Unstable Equilibrium Point method)分析系統的暫態穩定性時,需滿足單參數橫截性條件,而該條件是否成立與阻尼大小有關[2]。阻尼系數存在一個臨界值,當大于臨界值時,系統完全穩定。因此暫態過程中阻尼轉矩系數的研究具有重要意義。
由于計算速度的要求,大規模電力系統穩定分析中部分發電機需采用簡化模型。模型中阻尼系數設置為常數,來模擬阻尼繞組、網絡耗散特性、負荷、穩定控制裝置等多種阻尼因素的影響。而阻尼系數的取值往往根據經驗選取[1],其準確值尚難以確定。這是因為即使發電機選用詳細模型,阻尼轉矩蘊含在電磁轉矩中,仍難以準確獲得阻尼轉矩。
電力系統所經受的擾動可分為小擾動和大擾動。小擾動情況下,系統分析時可將系統方程線性化。其穩定平衡點不會發生變化。而大擾動下系統方程是非線性的,擾動前后穩定平衡點可能不同。 早期阻尼轉矩系數的研究主要針對小擾動模型。文獻[3]設同步轉矩系數和阻尼轉矩系數為常數,提出了一種轉矩分解方法—breaking algorithm。文獻[4-5]將電磁轉矩增量分解為阻尼轉矩增量和同步轉矩增量,通過仿真或實驗數據求取同步轉矩系數及阻尼轉矩系數。文獻[6]利用Prony 分析法計算了多機系統的阻尼轉矩系數。
由于大擾動情況下電力系統是高階非線性的,故小擾動分析法已不適用。暫態過程中關于阻尼系數計算的研究較少。文獻[7]利用派克方程推導了單機無窮大系統暫態過程中阻尼系數的解析表達式。文獻[8-9]假設功角作穩態正弦大振蕩,分解得到同步發電機的阻尼轉矩系數,指出阻尼轉矩系數不是常數。文獻[10]利用多項式逼近定理得到暫態過程中發電機的阻尼轉矩系數。
上述研究都是以交流系統為研究對象,由于電力系統已經由純交流系統發展為交直流混合電力系統。本文在文獻[10]的基礎上利用多項式逼近法求取交直流電力系統暫態過程中同步發電機的阻尼轉矩系數。并利用文獻[4-5]中的方法來檢驗本文方法的正確性。
1 大擾動下同步發電機阻尼轉矩系數計算
1.1 阻尼轉矩系數的數值分析方法
多項式逼近定理可實現對有界閉區間上連續多變量函數的有效逼近。文獻[10]給出了利用多項式逼近法(Weierstrass 逼近定理)計算阻尼轉矩系數的詳盡過程。在此不再詳述,直接給出暫態過程中電磁轉矩Te的逼近表達式。

式中,Pm為機械功率,δs為穩定平衡點角度,ωN為額定角速度。n、m分別為角度差和角速度偏差的最高指數,pij為相應的多項式系數,且p00=0。
當n、m和pij確定后,可得到電磁轉矩的近似表達式,并使逼近誤差滿足:

如果式(2)中的ε足夠小,則令Ps=P(δ,ωN),可近似得到同步轉矩Ts,進而可以獲得阻尼轉矩的近似值,并計算出阻尼轉矩系數:

由以上分析可知,計算阻尼轉矩系數需要設定夠小的逼近誤差ε,然后確定式(1)所示多項式函數的指數n和m,以及多項式系數pij。
下面介紹大擾動后,沿故障后軌線計算阻尼轉矩系數的步驟。設故障清除時間為tcl:
(1)在故障中軌線上取2k1+1 個點作為故障后軌線的起始點,即xh01=x(tcl+h1Δt1),h1=-k1,…,-1,0,1,…,k1,Δt1=tcl/100。
(2)通過仿真獲得2k1+1 條故障后軌線,在每 條故障后軌線上采樣k2個點,記錄每個采樣點的轉子角、轉子角 速度和電磁轉矩,即
(3)確定多項式系數pij。對于給定的一組指數n、m,可由采樣值得到(2k1+1)×k2個方程
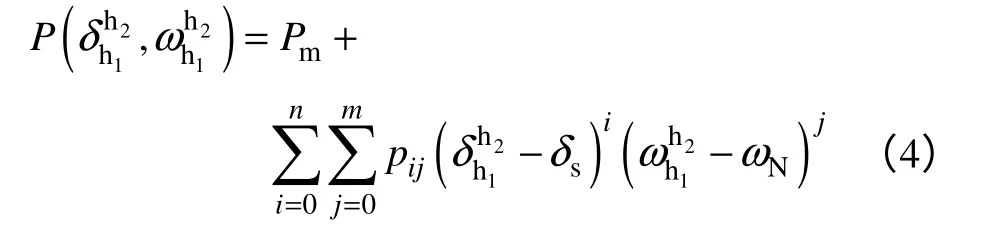
通過解式(5)所示的最小值問題,可確定(n+1)×(m+1)-1 個多項式系數pij。

設x=[p01,…,p0m,p10,…,p1m,…,pn0,…,pnm],上述最小值問題利用最小二乘法求解可得
式中,矩陣A、b示于本頁底部。
(4)系數pij確定后代入式(1)得到電磁轉矩的逼近值P(δ,ω),判斷逼近誤差是否滿足式(2)。若滿足,則第(3)步中給定的指數n、m可作為電磁轉矩逼近多項式(1)中的最大指數。如果不滿足則返回第(3)步,重新設定新的n、m值。
(5)n、m確定后,對于給定的故障切除時間,采用故障后仿真數據,通過式(1)計算P(δ,ω)。
(6)令多項式(1)中的角速度為額定角速度,得到Ps,作為同步轉矩Ts的近似值。
(7)從Te中減去Ps,得到阻尼轉矩近似值Pd。
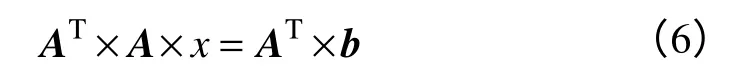
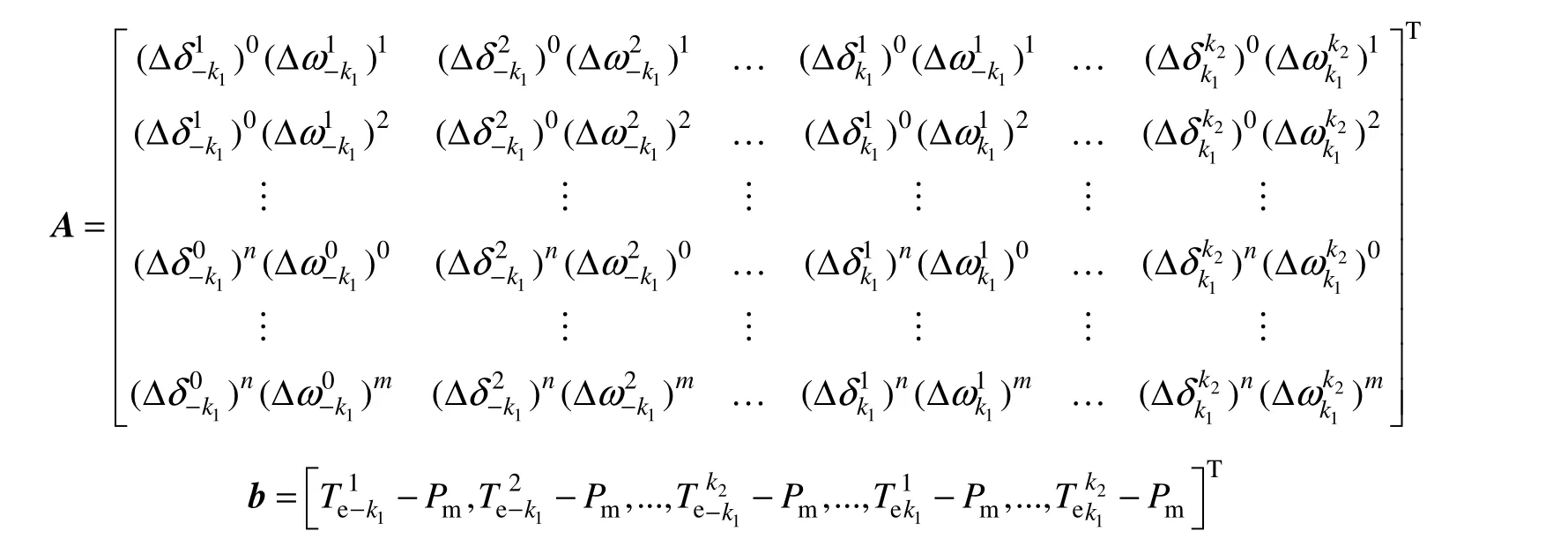
(8)用阻尼轉矩近似值除以角速度差,得到暫態過程中的阻尼轉矩系數D。
1.2 算例分析
本文研究的交直流系統如圖1所示。發電機通過兩條并聯線路,經理想變壓器與無窮大母線相連,一條直流線路與交流輸電線路并聯。系統中交流部分參數見文獻[1]。發電機初始電壓V=1.05,輸入機械功率Pm=0.8。負荷p=0.6,q=0.4,為恒功率負荷。發電機模型采用七階模型,考慮一階勵磁系統作用。直流輸電系統參數見文獻[11]。直流輸電系統采用準穩態模型。整流側采用定電流控制Ids=0.1,逆變側采用定熄弧角控制,γ=22°。定電流控制調節器的比例和積分參數為:K1=0.5,T1=2。定熄弧角控制調節器的比例和積分參數為:K2=0.5,T2=2。
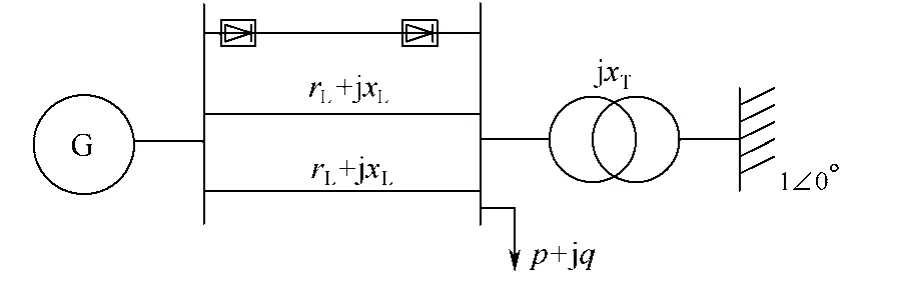
圖1 單機無窮大交直流電力系統
上述系統經受快關氣門擾動,擾動持續時間為0.05s,故障后仿真15s。仿真計算得到系統的電磁轉矩Te、功角δ、角速度ω曲線如圖2所示。

圖2 交直流系統電磁轉矩、功角、角速度差的仿真曲線
由圖2可知系統在上述擾動下是暫態穩定的。系統各物理量均恢復到原平衡點。
利用多項式逼近法對電磁轉矩進行分解,最終得到發電機的阻尼轉矩系數如圖3所示。

圖3 交直流系統暫態過程中發電機的阻尼轉矩系數
由圖3可知在暫態過程中發電機的阻尼轉矩系數D是變化的,在暫態初期波動范圍較大,最大值為5.6,最小值為3.8。t>5s 后波動范圍較小,隨著系統的穩定阻尼轉矩系數最終值穩定在4.9 附近。由分析可得暫態穩定系統的阻尼轉矩系數在暫態過程結束后其值趨向于常數。
本文所采用的多項式逼近法沒有采用線性化假設,故其可用于大擾動和小擾動的阻尼轉矩系數計算。因尚無其他算法檢驗暫態過程中發電機阻尼轉矩系數計算的正確性。由圖2可知t>5s 后發電機各物理量波動較小,可視5s后的動態過程為小擾動。利用小擾動的阻尼轉矩系數方法計算該算例t>5s后發電機的阻尼轉矩系數,與本文方法得到的結果比較。間接驗證本文方法的正確性。
2 阻尼轉矩系數計算結果的討論
文獻[4-5]提出了系統受到小擾動時電磁轉矩系數的算法。在系統動態過程中將電磁轉矩增量分解為阻尼轉矩增量和同步轉矩增量。阻尼轉矩增量與角速度變化成比例,同步轉矩增量同功角變化成比例。并假設阻尼轉矩系數和同步轉矩系數均為常數。因此,轉矩增量可表示為

式中,ΔTe為電磁轉矩變化量;Ks、Kd分別為同步轉矩系數和阻尼轉矩系數;Δδ、Δω分別為功角變化量和角速度變化量。
利用最小二乘法通過動態仿真或實驗數據求取電磁轉矩系數。Ks、Kd由式(8)、式(9)求得

通過對時域仿真得到的ΔTe、Δδ、Δω進行數值積分得到式(8)、式(9)中的各積分項。進而得到同步轉矩系數Ks和阻尼轉矩系數Kd。
上述算法能夠計算出小擾動下發電機的同步和阻尼轉矩系數。采用本文提出的方法對大擾動和小擾動情況均適用,故對小擾動的計算結果應當與上述方法一致;否則,難以保證大擾動下阻尼轉矩系數計算結果的正確性。
下面首先采用上述算法計算大擾動振蕩基本平息后的電磁轉矩系數。利用故障清除后5~15s 的仿真數據,計算本文2.2 節算例中同步發電機的阻尼轉矩系數。其結果示于圖4。由圖4可得5~15s 之間Kd的值基本一致,其值大小在4.9 左右。說明該算法對本文算例是有效的。

圖4 小擾動算法得到的t>5s 后的阻尼轉矩系數
將圖4與圖3中t>5s 后的阻尼轉矩系數進行比較。由圖3可見,t>5s 后的波動范圍較小,并逐漸趨于4.9。兩種算法得到的結果相差小于0.01,可以認為結果是一致的。間接驗證了該文方法在暫態過程中發電機阻尼轉矩系數計算的有效性。
3 結論
本文利用多項式逼近法求取交直流電力系統暫態過程中同步發電機的阻尼轉矩系數,結果顯示,暫態過程中阻尼轉矩系數不是常數。對于穩定系統,隨著振蕩逐漸平息,阻尼轉矩系數也趨于一個穩態值。采用多項式逼近法計算得到的阻尼轉矩系數的最終值,與利用小擾動模型阻尼系數計算方法計算暫態基本平息后的阻尼轉矩系數基本一致,驗證了本文方法的正確性。
[1] Kundur P.Power system stability and control[M].New York: Mc Graw-hill,1994.
[2] Alberto L C,Bretas N G.Required damping to assure multiswing transient stability:The SMIB case[J].International Journal of Electrical Power&Energy System,2000,22(3): 179-185.
[3] De Mello F P.Concordia C.concepts of synchronous machine stability as affected by excitation control[J].IEEE Transaction on Power Apparatus and System,1969,88(4): 316-329.
[4] Alden R H,Shaltout A A.Analysis of damping and synchroning torques part I-A general calculation method[J].IEEE Transactions on Power Apparatus and Systems,1979(5): 1696-1700.
[5] Alden R H,Shaltout A A.Analysis of damping and synchroning torques part II-A general calculation method[J].IEEE Transactions on Power Apparatus and Systems,1979,PAS-98(5): 1701-1708.
[6] 李鵬,余貽鑫,孫強,等.基于Prony 分析的多機系統電磁轉矩系數計算[J].電網技術,2006,30(10): 39-44.
[7] 張鈺,王英.杜阿美爾積分法求阻尼轉矩和阻尼功率[J].太原理工大學學報,1998,29(2): 90-93,97.
[8] 湯蘊璆,王艷萍.功角作正弦大振蕩時同步電機的整步轉矩和阻尼轉矩系數[J].哈爾濱電工學院學報,1990,13(1): 1-14.
[9] 王艷萍.功角作正弦大振蕩時定子電阻對同步電機整步轉矩和阻尼轉矩系數的影響[J].哈爾濱電工學院學報,1991,14(2): 129-132.
[10] Jiang Ningqiang,Chiang HD.Numerical investigation on the damping property in power system transient behavior[J].IEEE Transactions on Power Systems,2013,28(3): 2986-2993.
[11] 徐政.交直流電力系統動態行為分析[M].北京: 機械工業出版社,2004.

