波浪作用下粉質土海床累積孔隙水壓力簡化分析?

王 虎， 劉紅軍,2

(中國海洋大學 1. 海洋環境與生態教育部重點實驗室； 2. 環境科學與工程學院， 山東 青島 266100)

?

波浪作用下粉質土海床累積孔隙水壓力簡化分析?

王 虎1， 劉紅軍1,2

(中國海洋大學 1. 海洋環境與生態教育部重點實驗室； 2. 環境科學與工程學院， 山東 青島 266100)

波浪引起的孔隙水壓力直接影響海床地基穩定性，而累積孔隙水壓力是細顆粒弱粘性粉質土的主要響應形式。針對在海岸和近海廣泛分布的粉質土，基于一維固結理論，采用更適于描述粉質土動力特性的雙曲線型孔隙水壓力發展模式作為源項，推導相應的有限差分格式，并在MATLAB環境下進行編程求解，給出波浪作用下粉質土海床累積孔隙水壓力響應的簡化分析方法。以黃河三角洲為背景的算例顯示，本文所給的模型和計算方法高效、易行，可為相關的海岸與海洋工程設計提供理論參考和技術支持。

波浪荷載；粉土；累積孔隙水壓力；固結方程；有限差分；黃河三角洲

波浪作用下孔隙水壓力的發展變化直接影響海床地基穩定性，威脅海洋工程的安全穩定和正常使用[1-2]。例如，以粉質土為代表性土類的黃河三角洲地區[3-4]，廣泛發育有海底滑坡、塌陷凹坑、粉砂流沖溝等海底地質災害和災害地貌[5-6]，曾發生海底電纜彎折[3]和平臺失穩[7]的案例。研究表明，風暴潮伴隨的極端波浪與粉質土海床相互作用所引起的孔隙水壓力變化是上述地質災害和海洋工程失穩的重要誘因[3,7-8]。粉質土介于砂土和黏土之間，具有相對特殊的物理性質和靜、動力學性質，且在海岸和近海地區廣泛分布[9]，因此，研究波浪作用下粉質土海床的孔隙水壓力響應具有重要意義。

波浪作用下海床孔隙水壓力響應有瞬態和累積兩種機制：瞬態孔隙水壓力圍繞平衡位置往復振蕩，累積孔隙水壓力從初始值累積升高[1-2]。瞬態機制多對應于較小的波浪與較大剛性的粗顆粒土組合；而對于極端波浪與細顆粒弱黏性粉質土的組合，累積機制則占主導地位[2]。室內水槽試驗[10]和現場試驗[11]均發現波浪引起細粒土海床中明顯的孔隙水壓力累積升高。

波浪作用下海床累積孔隙水壓力的計算方法中，二維彈塑性模型[12]的參數獲取和計算實現較為復雜，簡便易行的是將其簡化為一維問題，以帶源項的一維固結方程作為控制方程，將基于土的動力試驗獲得的孔隙水壓力發展模式作為源項，將波浪循環荷載作為唯一外荷載，研究豎向海床孔隙水壓力隨時間的發展變化[2,13-17]。孔隙水壓力發展模式因土體自身狀態及所施加外荷載的不同而具有多種形式，當前已被應用于計算的有經典的砂土反正弦型[13]、簡化的線性型[7,14-15]、考慮砂土主應力旋轉[16]及考慮加載歷史[17]的發展模式。研究表明，雙曲線型的孔隙水壓力發展模式更適于描述粉質土的動力響應[9,17-20]，但目前為止，鮮見應用雙曲線型發展模式計算波浪作用下海床累積孔隙水壓力的相關研究。

鑒于此，本文基于一維固結理論，采用雙曲線型的孔隙水壓力發展模式作為源項，推導有限差分格式，在MATLAB環境下實現編程求解，建立一種波浪作用下粉質土海床累積孔隙水壓力響應的簡化分析方法。以黃河三角洲為例，應用現場的波浪參數和土層土性參數，研究波浪作用下粉質土海床的累積孔隙水壓力響應，并討論其響應機制。

1 基本方程

海水覆蓋的海床是由土顆粒和孔隙水組成的典型固、液兩相飽和土，適用于經典的Tergazhi一維滲流固結理論[21]。一維情況下的Biot固結方程與Terzaghi固結方程具有相同的形式，該方程建立在以下假設之上：土體均質各向同性，線彈性，小變形，滲流符合達西定律。將該方程作為波浪作用下海床累積孔隙水壓力響應的控制方程，表達式為：

(1)

式中：u為累積孔隙水壓力；t為時間；cv為土的固結系數；z為海床深度(海床表面為零，向下為正方向)；f為源項即孔隙水壓力發展模式。式(1)這一形式的方程是一種典型的拋物線型偏微分方程，也被用于研究熱傳導或有源擴散問題。

假設海床表面自由排水，無限深海床底部剛性隔水；海床各層之間滿足孔隙水壓力連續和流速連續條件；波浪作用之前整個海床的累積孔隙水壓力為零。邊界條件、層間連續條件和初始條件表示為：

(2)

(3)

u(z,0)=0。

(4)

式中：k為滲透系數；i為土層編號。

孔隙水壓力發展模式及其參數的選取，直接影響到計算的準確性[18]。本文采用劉紅軍等[20]建立的黃河三角洲粉質土的雙曲線型孔隙水壓力發展模式：

(5)

式中：σ0’為初始豎向有效應力，可通過σ0’=γ；z計算；γ；為土體浮容重；N為動荷載循環次數；Nl為累積孔隙水壓力達到液化或穩定時的循環次數，a、b、c為經驗系數。N和Nl的表達式[14]為：

(6)

(7)

式中：T為波浪周期；α、β為與土的類型及相對密度相關的參數；τ為波浪引起的海床內剪應力幅值。聯立式(5)、(6)，孔隙水壓力發展模式f可寫成：

(8)

式(7)中波浪引起的剪應力幅值τ，采用Biot方程計算，并且假設孔隙水壓力累積過程中τ不變[2,13-17]。當海床深度大于半個波長之時，τ的表達式為：

τ=P0λzexp(-λz)。

(9)

式中：λ為波數(λ=2π/L)；L為波長；P0為床面動水壓力幅值：

(10)

式中：γw為海水容重；H為波高；d為水深。聯立式(7)～(10)可得f的表達式，再結合式(1)～(4)，構成波浪作用下海床累積孔隙水壓力響應初邊值問題的基本數學表達。

2 有限差分求解及驗證

采用有限差分法對初邊值問題進行求解，在平面區域z-t方向做矩形網格剖分，h=z/M，Δt=t/N分別為空間和時間步長，M、N分別為空間和時間步數。采用具有二階精度并且無條件穩定的Crank-Nicolson差分格式進行離散，表示如下：

(11)

為方便起見，將網格比記為：

(12)

對式(11)進行整理，得到由第k時間層向第k+1時間層計算累積孔隙水壓力的三對角方程組：

(13)

此方程組系數矩陣嚴格對角占優，存在唯一解，在MATLAB環境下編程求解。

若式(1)不含源項f，則退化為經典的Terzaghi一維固結方程，為驗證本文差分格式和求解程序的有效性，將退化方程的差分解與解析解[21]進行比較，參數取為：均質土層厚度z=20m，表層單面排水，表面瞬時均布荷載100kPa，即整個土層的初始超孔隙水壓力值u0=100kPa，固結系數Cv=0.002 m2/s，取10000s時的超孔隙水壓力值輸出，如圖1所示，二者具有較好的一致性。

圖1 差分解與解析解比較

3 波浪作用下黃河三角洲粉質土海床累積孔隙水壓力響應

以黃河三角洲埕島海域為背景，計算中考慮了不同水深條件下5年一遇和50年一遇2種類型的波浪[7-8,12]，如表1所示。計算中采用了粉砂、粉土、粉質黏土3種類型的均質海床，同時研究了文獻[4]所述的上部有2m厚度的粉土硬殼層，下部為粉質黏土的地層組合，簡稱為“雙層海床”。計算中海床厚度取為40m，以保證其大于半個波長從而剪應力幅值滿足式(9)，空間步長取為0.5m。時間步長取為1s，參照風暴潮的持續作用時間，最長計算到120min。參照文獻[7,12,21]得到土體浮容重和固結系數，根據文獻[20]得到孔隙水壓力發展模式的參數。根據文獻[2,14-15]，公式(7)中參數取為α=0.246，β=-0.165。海床土參數詳見表2。

表1 波浪參數

Note： ①Water depth；②Ware with recarrence interval of fifty years；③Ware height；④Ware length；⑤Period

表2 海床土體參數

Note： ①Soil kind；②Submergedanit weight；③Wefficient of consolidation；④Parameter of poe water presult decpment model；⑤Sandy cilt；⑥Silt；⑦Silty clay

圖2(a)給出了10 m水深50年一遇波浪作用下均質粉土海床的響應，累積孔隙水壓力隨著時間增加不斷增大，其最大值約為40 kPa，出現在床面以下15 m左右。巖土工程師所關注的一個焦點是超孔隙水壓力與初始豎向有效應力的比值，即超孔隙水壓力比(u/σ0’)，u/σ0’越大海床失穩破壞的可能性越大。圖2(b)給出10 m海床深度范圍內u/σ0’的變化情況，可以看出u/σ0’在海床表層附近最大，最大值超過0.8，隨著深度的增加而逐漸減小，在10 m處已不足0.4，但均未超過1。

圖3給出了不同水深條件下50年一遇波浪作用60 min均質粉土海床的響應，累積孔隙水壓力隨著水深的增加不斷增大，8和10 m的累積超孔隙水壓力基本相等，表明在水深增大到8～10 m時50年一遇波浪對粉土海床的影響已達到最大。

圖4給出了不同波浪作用60min時10m水深均質粉土海床響應，可以看出波浪條件越極端，累積孔隙水壓力越大。

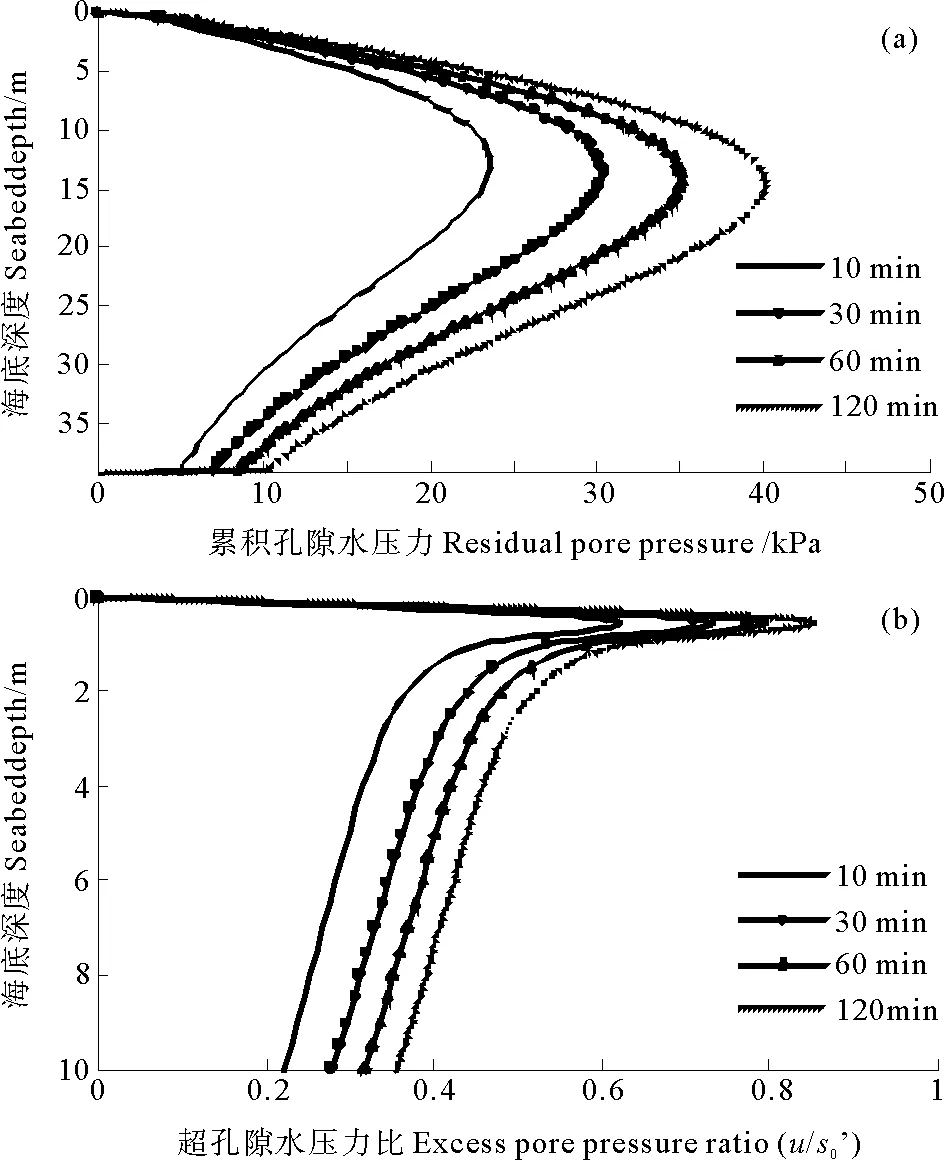
(10 m水深50年一遇波浪條件下均質粉土海床響應：(a)累積孔隙水壓力；(b)超孔隙水壓力比。for the case of homogeneous silty seabed under 50-year once wave with 10 m water depth: (a) residual pore pressure along depth; (b) excess pore pressure ratio along depth.)

圖2 時間對累積孔隙水壓力的影響
Fig.2 Effects of time on residual pore pressure response

(50年一遇波浪作用60 min均質粉土海床響應。(for the case of homogeneous silty seabed under 50-year once wave with duration of 60 min,)

圖3 水深對累積孔隙水壓力的影響
Fig.3 Effects of water depth on residual pore pressure response

圖5為10m水深粉砂、粉土、粉質黏土3種均質海床以及雙層海床在50年一遇波浪作用60min時的累積孔隙水壓力曲線。從圖中可以看出，均質粉土和粉質黏土海床的孔隙水壓力累積幅度大致相等，粉質黏土海床的累積孔隙水壓力最大值出現的深度略大于粉土海床。均質粉土和粉質黏土的孔隙水壓力累積幅度大于粉砂海床，可能是粉砂滲透性相對較好引起部分超孔隙水壓力消散所致。雙層海床與均質粉質黏土海床的累積孔隙水壓力曲線幾乎完全重合，分析可能是雙層海床表面粉土層厚度僅有2 m，且粉土與粉質粘土的孔隙水壓力發展模式及參數比較接近所致。

(10m水深均質粉土海床波浪作用60min。The case of homogeneous silty seabed with water depth of 10 m and wave duration of 60 min.)

圖4 波浪條件對累積孔隙水壓力的影響
Fig.4 Effects of wave conditions on residual pore pressure response

(10 m水深50年一遇波浪作用60 min均質海床響應。The case of homogeneous seabed with 10 m water depth and duration of 60min under 50-year once waves.)

圖5 海床土層土性對累積孔隙水壓力的影響
Fig.5 Effects of soil parameters on residual pore pressure response

圖2～5的計算結果顯示，不同波浪和海床組合下，最大超孔隙水壓力約為40 kPa，其最大超孔隙水壓力比u/σ0’約為0.8，即沒有達到完全的液化。分析其原因：首先，相對于地震荷載，波浪荷載頻率相對較低、強度相對較低，孔隙水壓力累積速度相對較慢；波浪持續時間相對較長，以及海床表面自由排水的邊界條件使得累積過程中部分孔隙水壓力消散。其次，粉質土的孔隙水壓力發展模式不同于砂土，粉質土中含有的少量黏粒成分限制了孔隙水壓力的進一步累積升高，在尚未達到完全液化的情況下應變即已持續發展，這一點在土的不排水動力試驗[9,20]和室內水槽試驗[10]中均得到了驗證。因此，波浪作用下粉質土海床不一定會出現超孔隙水壓力比u/σ0’達到1的完全液化。按照有效應力原理，自由海床的累積孔隙水壓力不可能超過有效應力，即超孔隙水壓力比不能超過1，計算結果顯示了本文模型的可靠性，避免了之前研究[2,8,13-16]中超孔隙水壓力比超可能過1的錯誤情況。

值得注意的是，除完全液化之外，還存在沖刷和剪切破壞等海床失穩形式[1]。孔隙水壓力的累積升高總會增大海床地基及結構物失穩破壞的幾率，例如：累積孔隙水壓力能夠引起自下而上的滲流力，促進泥沙的起動和沖刷；累積孔隙水壓力能夠降低海床土的有效抗剪強度，進而誘發海底滑坡；累積孔隙水壓力能夠降低樁基承載力和管線的穩定性。本文給出的模型和算法簡便、可靠，可為相應的海洋工程設計提供一定的參考和支持。

5 結論

(1)基于一維固結方程和雙曲線型的孔隙水壓力發展模式，采用有限差分方法并在MATAB編程求解，可簡便、有效地實現波浪作用下粉質土海床的累積孔隙水壓力響應分析。

(2)以黃河三角洲為背景的計算結果顯示，粉質土海床中累積孔隙水壓力隨波浪持續時間的增加而增大，隨波浪的劇烈程度增加而增大，在水深增大到8m時達到最大，均質粉土和粉質黏土海床中累積孔隙水壓力大于粉砂海床，表面硬殼層的影響不明顯。波浪引起的海床超孔隙水壓力比在表層1m左右最大，但均未超過1，即可能發生除液化之外的其他形式的海床失穩。

[1] Sumer B M, Freds?e J. The mechanics of scour in the marine environment [M]. Singapore: World Scientific, 2002.

[2] Jeng D S, Seymour B R, Li J. A new approximation for pore pressure accumulation in marine sediment due to water waves [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(1): 53-69.

[3] 許國輝, 王欣, 劉會欣, 等. 粉質土海岸微地貌形成及泥沙問題的工程地質分析 [J]. 海洋地質與第四紀地質, 2010, 30(2): 43-50.

[4] 馮秀麗, 林霖. 現代黃河水下三角洲全新世以來土層巖土工程參數與沉積環境之間的關系 [J]. 海岸工程, 1999, 18(4): 1-7.

[5] 周良勇, 劉健, 劉錫清, 等. 現代黃河三角洲濱淺海區的災害地質 [J]. 海洋地質與第四紀地質, 2004, 24(3): 19-27.

[6] 李海東, 楊作升, 王厚杰, 等. 現代黃河水下三角洲地質災害現象的空間分布 [J]. 海洋地質與第四紀地質, 2006, 26(4): 37-43.

[7] 楊少麗, 沈渭銓, 楊作升. 波浪作用下海底粉砂液化的機理分析 [J]. 巖土工程學報, 1995, 17(4): 28-37.

[8] 孫永福, 董立峰, 宋玉鵬. 黃河水下三角洲粉質土擾動土層特征及成因探析 [J]. 巖土力學, 2008, 29(6): 1494-1499.

[9] 曹成效, 劉樂軍, 李培英, 等. 循環荷載作用下粉土的動力學特性 [J]. 海洋科學進展, 2007, 25(1): 54-62.

[10] Tzang S Y, Ou S H. Laboratory flume studies on monochromatic wave-fine sandy bed interactions: Part 1. Soil fluidization [J]. Coastal engineering, 2006, 53(11): 965-982.

[11] Sassa S, Takayama T, Mizutani M, et al. Field observations of the build-up and dissipation of residual pore water pressures in seabed sands under the passage of storm waves [J]. Journal of Coastal Research, 2006, 39: 410-414.

[12] 劉紅軍, 王虎, 張民生, 等. 波浪作用下黃河三角洲粉質土海床動力響應分析 [J]. 巖土力學, 2013, 34(7): 2065-2071.

[13] Seed H B, Rahman M S. Wave-induced pore pressure in relation to ocean floor stability of cohesionless soils [J]. Marine Georesources & Geotechnology, 1978, 3(2): 123-150.

[14] McDougal W G, Tsai Y T, Liu P L F, et al. Wave-induced pore water presure accumulation in marine soils [J]. Journal of Offshore Mechanics and Arctic Engineering, 1989 (111): 1-11.

[15] Cheng L, Sumer B M, Freds?e J. Solutions of pore pressure build up due to progressive waves [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(9): 885-907.

[16] 欒茂田, 張晨明, 王棟, 等. 波浪作用下海床孔隙水壓力發展過程與液化的數值分析 [J]. 水利學報, 2004, 2: 94-100.

[17] 潘冬子, 王立忠, 潘存鴻. 粉質海床波浪響應的數值模擬及試驗研究 [J]. 巖土力學, 2008, 29(10): 2697-2707.

[18] 張建民, 謝定義. 飽和砂土振孔隙水壓力增長的實用算法 [J]. 水利學報, 1991 (8): 45-51.

[19] 曾長女, 劉漢龍, 豐土根, 等. 飽和粉土孔隙水壓力性狀試驗研究 [J]. 巖土力學, 2005, 26(12): 1963-1966.

[20] 劉紅軍, 王小花, 賈永剛, 等. 黃河三角洲飽和粉土液化特性及孔壓模型試驗研究 [J]. 巖土力學, 2005, 26(10): 83-87.

[21] 錢家歡, 殷宗澤. 土工原理與計算(第二版) [M]. 北京： 中國水利水電出版社, 1996: 200-201.

責任編輯 徐 環

A Simplified Analysis Method for Residual Pore Pressure Response of Silty Seabed Under Wave Loads

WANG Hu1, LIU Hong-Jun1,2

(1. The Key Laboratory of Marine Environment and Ecology, Ministry of Education; 2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China)

The stability of seabed foundation is threatened by the wave-induced pore pressure, and residual pore pressure response is dominant for feebly cohesive fine-grained silty seabed under wave loads. For the widely distributed silty soil in coastal areas, the basic equations of wave-induced residual pore pressure in silty seabed is established based on the one-dimensional consolidation theory, in which a hyperbolic-shaped pore pressure development mode is particularly chosen as a source term. Finite differential scheme of the initial boundary value problem is derived and solved in MATLAB. The proposed model and corresponding algorithm are proved to be effective through the case study in the Yellow River delta, and can provide theoretic reference and technique support for the design of coastal and ocean engineering.

wave loads; silt; residual pore pressure; consolidation equation; finite difference; Yellow River delta

國家自然科學基金項目(41572247)；山東省科技發展計劃項目(2014GGX104007)資助

2014-09-01；

2014-11-23

王 虎(1986-)，男，博士生。E-mail: wanghu824@126.com

TU431; TU392.5

A

1672-5174(2015)11-075-06

10.16441/j.cnki.hdxb.20140253