應用型本科高校線性代數教學改革探討

王 貞

（池州學院 數學與計算機科學系，安徽 池州 247000）

1 應用型本科高校線性代數教學現狀

1.1 教材重理論輕應用

線性代數教材，以同濟六版[1]為例，主要介紹定義、定理和相關計算，內容重理論、偏抽象，對一些概念的背景來源，知識的實際應用等方面則很少涉及。對于應用型本科高校來說，這樣的教學內容很難使學生對其產生興趣，更重要的是，它不符合應用型人才培養需求。

1.2 教學課時不足，教學內容受限

線性代數教學時數有限，一般為32-48課時。課時較少，內容抽象，其內容為：行列式、矩陣及其運算、矩陣的初等變化與線性方程組、向量組的線性相關性、相似矩陣與二次型等，對于其核心內容“線性空間與線性變換”就只能點到為止。由于課時不足，致使學生沒學到線性代數的精華內容。

1.3 考核制度不完善

線性代數課程考核，主要考查平時出勤率以及期末卷面成績。期末試卷，主要是考查學生對基本概念的理解，以及判斷、計算、推理、證明等，缺少對解決實際問題能力的考核。這樣的考核制度，導致很多學生只注重理論知識的學習，忽視了能力培養。

2 應用型本科高校線性代數教學改革思路

2.1 教學內容改革

2.1.1 增加實際應用背景知識 當前很多教材，主要介紹基礎知識，缺乏知識來源和聯系實際生活等內容，學生學習起來，感覺枯燥無味。因此，我們可以借鑒美國著名教育家David Lay教授編著的《線性代數及其應用》[2]，適當插入一些背景知識或者與我們身邊相關的實際生活問題，提高學生學習興趣，促進學生自主學習。

2.1.2 精煉教學內容，突出重點內容 李尚志老師認為，線性代數主要內容：空間為體，矩陣為用[4]。我們講解矩陣內容時，要突出其重點地位，根據應用型人才培養目標，引用一些具體實例，如人口遷移問題等，努力培養學生利用矩陣解決實際問題的能力。行列式的計算并不是線性代數的重點內容，我們只需利用行列式性質掌握一些基本的計算方法即可。我們需要向學生介紹如何利用Matlab計算行列式，在很多實際問題中關于行列式的計算都用Matlab執行。此外，對于克拉默法則，同學們只需知道這個法則即可，不需要利用這個法則來解給定的方程組。

2.1.3 根據內容采用分層教學 由于教學課時有限，教學內容很難滿足所有同學的需求。為了解決這個問題，我們可以采取分層教學模式，在大二上學期，面向全體理工、經管等專業學生，開設線性代數公共課；在大三上學期或下學期，面向繼續深造或者對線性代數感興趣的學生，開設線性代數選修課。線性代數公共課，內容基礎，突出應用；線性代數選修課，深化理論知識，培養學生的邏輯思維能力，為進一步夯實基礎。

2.2 教學方法改革

2.2.1 整體性教學 在授課過程中，我們要善于引導學生注意前后知識的銜接，幫助學生系統性掌握基礎知識。例如判斷n維向量組A:α1,α2,…,αm的線性相關性，可以通過判斷線性方程組x1α1+x2α2+…+xmαm=0 是否有非零解。而對線性方程組求解問題，我們只需比較矩陣A=(α1,α2,…,αm)的秩與m的大小關系。從這樣問題出發，可以將矩陣、線性方程組的解、向量組的線性相關性內容聯系起來，形成一個整體。

2.2.2 借助計算機輔助教學 當我們還一如既往地講解行列式的計算方法、求逆矩陣、解線性方程組時，我們的學生很難解決實際生活中的數學問題。例如，Wassliy Leontief利用500個變量的500個線性方程問題描述美國經濟問題[3]。解這樣的線性方程組，如果純粹手算，是一件繁冗復雜的事情。我們可以引入Matlab數學軟件來解決這一問題。此外，Matlab軟件還可以求解行列式、方陣的逆、線性方程組、特征值、特征向量等問題，有效幫助助學生解決實際生活問題。

2.2.3 以學生為中心 教學過程中，我們要以學生為中心，尊重學生經驗。例如，我們在講解施密特正交化的時候，可以先給定線性無關的向量組a1,a2，如何由這組向量組得出兩個正交的向量組呢？我們可以以a1為給定向量，將a2沿著a1方向和垂直a1方向進行分解，分別得到向量a'2和b2，從而使得b2⊥a1，接下來如何由a1,a2表示b2呢？以問題為突破口，誘導學生思考，以幾何為工具，加強學生感性認識。最后，由這樣簡單直觀的情況延伸到空間中的3個線性無關組正交化，繼而抽象到n(n＞3)個線性無關的向量組如何正交化問題，施密特正交化過程也就不再生澀難懂了。

2.2.4 以應用為導向 我們在講解某些知識點時，可以引入一些實際應用問題，從而激發學生學習興趣，增強學習動力。例如，我們在講解矩陣的運算以及矩陣的逆的時候，可以引入利用矩陣編制Hill密碼問題[6]。比如我們要發出信息linear，現需要利用矩陣乘法給出加密方法和加密后得到的密文，并給出相應的揭秘方法。假定空格和26個英文字母依次對應整數0～26（見下表）。

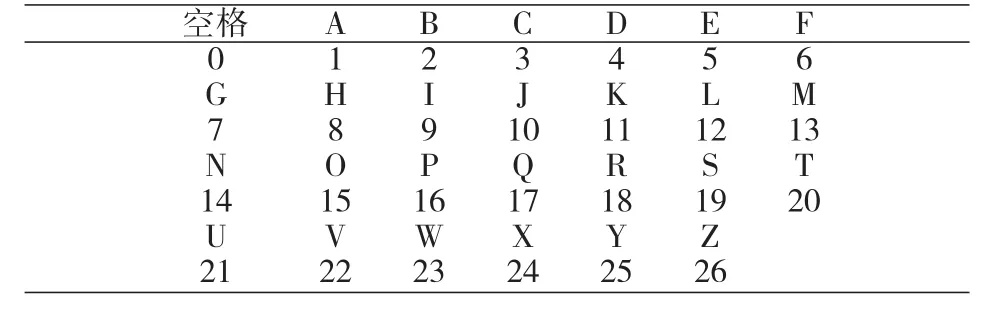
空格及字母的整數代碼表

假設單詞從左到右，每3個字母分為一組，并將對應的3個整數排成3維的行向量。

通過以上所述假定，信息linear對應兩個向量x1=(12,9,14)，x2=(5,1,18).我們給定可逆矩陣

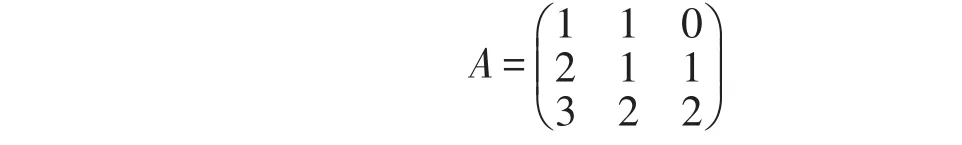
使得密文

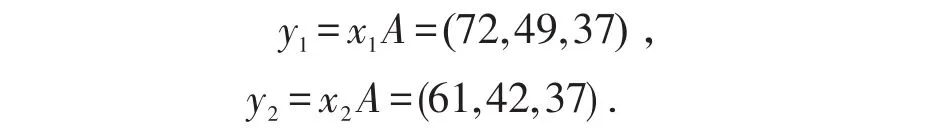
接收方收到的密文是72，49，37，61，42，37.接收方需要解碼，則需要計算 (72,49,37)A-1和(61,42,37)A-1。

2.3 考核改革

對于線性代數的考核主要體現在三個方面：期末考試、實踐教學、平時出勤與作業，它們占總評成績比例可設為5:3:2。對于實踐教學的考查，可以放在某些章節結束后即可考查，這樣可以避免期末考前突擊現象的發生。

3 結束語

MIT的G.Strang教授提出“讓線性代數向世界開放”口號，我希望通過線性代數課程的教學改革，激發學生學習興趣，讓更多同學不僅能夠掌握其基本知識，還善于利用這些知識去解決一些實際問題，提高自己在現代社會中的競爭力。

[1]同濟大學數學系.工程數學線性代數[M].6版.北京：高等教育出版社，2014.

[2]David C Lay.Linear and its applications[M].4th Ed.New Jersey:John Wiley&Sons，Inc，2009.

[3]陳懷琛，龔杰民.線性代數實踐及Matlab入門[M]，北京：電子工業出版社，2005.

[4]李尚志.線性代數教學改革漫談[J].教育與現代，2004(01):30-31.

[5]Stang G.Introduction to Linear Algebra[M].3rd ed.Wellesley MA:Welley-CambridgePress，2009.

[6]楊威，高樹屏，線性代數計算與應用指導[M].西安：西安電子科技大學出版社，2009（4）:98-102.