一種新型混合粒子群算法及其在輸電網規劃中的應用

高明，周浩

(國網吐魯番供電公司，新疆 吐魯番 838000)

一種新型混合粒子群算法及其在輸電網規劃中的應用

高明，周浩

(國網吐魯番供電公司，新疆 吐魯番 838000)

輸電網規劃是一個規模巨大、極其復雜的、具有非線性離散變量和多約束多目標的數學優化問題。將一種融合了交叉和變異，以及結合混沌理論的新型混合粒子群算法應用到了求解輸電網規劃問題中。相對于普通粒子群算法，改進過的混合粒子群算法可以更快速有效地尋找到全局最優解。最后，通過算例驗證了算法應用于輸電網規劃是有效性和可靠性。

輸電網規劃；粒子群算法；交叉；變異；混沌

1 引言

輸電網規劃是電力系統規劃的重要組成部分，其任務是根據規劃期間的負荷增長及電源規劃方案確定相應的最佳電網結構，以滿足經濟可靠地輸送電能的要求[1]。人工智能理論和技術的快速發展，已經有很多基于人工智能的優化方法被應用到輸電網優化規劃中，比如遺傳算法GA[2-4]、蟻群算法ACA[5-8]、模擬退火算法SA[9]、進化規劃算法[10]等。

粒子群優化算法(PSO) 是美國學者Kennedy[11]在1995年提出來的，通過群體中個體之間的協作和信息共享來尋找最優解是算法的基本思想。但在應用到實際問題當中，PSO 也表現出了一些不盡人意的問題。這些問題中最主要的是它容易產生早熟收斂、全局尋優能力較差等。

鑒于以上不足，本文引入了一種新型混合粒子群算法[15]，它通過融合遺傳算法的交叉變異并引入混沌優化算法，將混沌理論與粒子群優化算法結合，提出了混沌粒子群算法。結合遺傳算法和混沌理論的思想，采用交叉機制增加種群的多樣性，同時提出與種群進化代數相關的自適應的混沌擾動機制和變異機制，增強早熟粒子跳出局部極值的能力。將該算法應用在輸電網規劃中取得了較好的效果。

2 PSO的基本原理

設搜索空間為D維，粒子總數為n。第i個粒子位置表示為向量Xi=(xi1xi2…xid)；第i個粒子的歷史最優位置為Pi=(pi1pi2…pi3)，其中為所有pi(i=1,2,3,…)中的最優；第i個粒子的速度為向量Vi=(vi1vi2…vi3)。每個粒子的速度和位置按如下公式進行變化：

vid(k+1)=w×vid(k)+c1r1(pid-xid)+c1r1(pgd-xid)

(1)

xid(k)=xid(k)+vid(k+1)

(2)

式中：i=1…m；學習因子c1和c2為非負常數；r1和r2為介于[0,1]之間的隨機數；慣性權重w為一個位于區間[0,1]中的常數；k為迭代次數；x1為第i個粒子的位置向量；vi為速度向量；Δt為時間間隔，通常取為單位時間。有學者研究了w對粒子群全局優化性能和收斂性能的影響,文獻[12]提出一種線性遞減慣性權重粒子群算法( LDWPSO)，其確定權重的公式如下：

w=wmax-t(wmax-wmin)/Tmax

(3)

式中wmax為最大慣性權重，wmin為最小慣性權重，t為當前進化代數，Tmax為最大進化代數。通過線性遞減慣性權重粒子群算法已成為一個標準，是檢驗新提出的方法的有效性。該算法在迭代初期給予w一個較大的值，一定程度上增加了種群的多樣性，在算法后期w有一個較小的值，有利于算法收斂和提高解的精度。但是該方法只是對w進行了簡單變換，在求解復雜的函數優化問題中，仍難以跳出局部極值。

3 CMCPSO的基本原理[15]

3.1 初始化策略

粒子群初始化對算法的性能產生一定影響，基本粒子群的初始化過程是隨機的，文獻[13]提出最好將粒子均勻初始化在解的空間中，假如初始的解群比較好，對于求解效率與解的質量都會有幫助。我們可以根據混沌具有不重復的遍歷性和偽隨機特性來初始化粒子的位置和速度，從而提高種群的多樣性。本文用到的是Logistic映射, 其定義如下

zk+1=μzk(1-zk),{zk|k=1,2,3…}

(4)

式中,μ為混沌因子，zk為實值序列，研究表明，當3.571448≤μ≤4時, 該混沌映射處于混沌狀態，在某一初始條件z1下，由Logistic映射生成序列為{zk|k=1,2,3,…}, 具有混沌序列特性。

3.2 交叉策略

利用遺傳算法里的選擇、交叉操作增加粒子的多樣性，通過引入新的交叉機制增強群體粒子的優良特性，從而減小算法陷入局部極值的可能。在每一次的迭代過程中按適應度高低對所有N個粒子進行排序，選取適應度較高的一半粒子直接進入下一代，后一半粒子作為待交叉粒子，進行交叉操作。交叉策略為：最后一個粒子和后一半粒子中第一個粒子交叉，第二個粒子和倒數第二個粒子交叉，依此類推。即首先隨機產生交叉位Ci∈[1,D]，第i個粒子和第N×3/2+1-i個粒子的Ci～D位進行交換，其中i=N/2+1,N/2+2,…,(N×3-2)/4；然后計算交叉后新生成的粒子適應度；最后交叉前后的所有粒子通過適應度的高低進行排序，將未參加交叉操作的粒子與適應度高的一半粒子組成新的種群。這樣不僅保留了種群中的優秀個體，同時也使種群更加多樣化，增強種群全局尋優能力。

3.3 混沌擾動和變異機制

隨著迭代過程的進行，一旦算法陷入局部極值，粒子速度接近于零，種群多樣性就慢慢消失，部分粒子出現惰性，其他粒子很快聚集到這些惰性粒子附近并停止移動,這種現象稱為早熟現象。避免早熟現象的產生，必須要提高算法的適應性，利用混沌和變異的思想，將其加入到粒子群算法中，幫助粒子跳出局部極值。

如果目前搜索到的全局最優值連續T0代變化小于一個較小的值Δt，我們就可以認為算法已經陷入了局部最優，這時便可以利用混沌運動的遍歷性，將目前整個粒子群搜索到的最優位置為基礎產生混沌序列，重新生成N×3/4個粒子，替換按照速度更新公式更新的粒子，而這些粒子的當前搜索到的最優位置保持不變，具體實現過程如下。

(1)利用式(4)混沌映射，產生混沌序列矩陣

Chaos(1:N×3/4,1:D)

(2)產生自適應的擾動偏差

Bias(1:N×3/4,1:D)

=k(Tmax-t)Rnd(1:N×3/4,1:D)

將Chaos的各個分量載波到自適應擾動偏差Bias內，在全局最優粒子附近產生個新的粒子

Pop(i,1:D)=Pg(1:D)-Bias(i-1,1:D)

+2Bias(i-1,1:D)Chaos(i=1,1:D)

作為重要的施工材料-鋼筋會在雨水箱涵技術應用于道路施工期間進行制裝施工。①為了使鋼筋的使用質量得以保證，需要按照設計圖紙的要求進行采購，鋼筋的各種檢驗報告和出廠合格證書均要備好。為了使鋼筋使用質量與施工要求相符合，進入施工現場的鋼筋由監理單位安排的專人對其檢測[2]；②通過檢驗的鋼筋需由監理人員簽字確認才可以投入施工使用中。尤其重視制作鋼筋的焊接環節，嚴格核查焊接的全部過程，使其焊接表面保證平整光滑，才能使焊接縫隙自然平緩的過渡且與施工需求相符合；③按照實際的施工狀況和要求，在安裝鋼筋過程中對其間距進行科學設計，在墊層上放置墨線，與工程設計結合起來將底板鋼筋準擺放。

按公式將混沌序列引入到算法中，在迭代中產生局部最優解的領域點，使惰性粒子逃離束縛并快速搜尋到最優解。因此改進了傳統粒子群進化后期收斂速度慢、易陷入局部最優的缺點，有效地提高了算法收斂速度和精度。如果局部極小位置和全局最優位置相隔較遠的情況，僅僅通過混沌擾動有時也難以跳出局部最優，如果搜索到的全局最優值連續T0代變化小于一個較小的值Δ0{Δ0<Δ1}則隨機產生變異位Mi∈[1,D]，除全局最優粒子以外，任意選擇N×3/4個粒子進行變異操作，變異公式如下

xi,Mi=ai+(bi-ai)Rnd()

(5)

算法被執行的前期，全局極值更新很快，交叉粒子群優化起主要作用，混沌和變異起輔助作用；而在算法搜索后期，若全局極值反復迭代后變化不大，為加速尋優進程，加強粒子的再次尋優能力，則根據式(6)判斷，采取混沌擾動策略，增強對當前全局最優位置附近的空間的搜索，還是通過采用變異操作，這樣可以較大幅度搜索遠離當前全局最優位置的空間。

(6)

式中Pi代表第i代進化以后更新得到的全局最優目標值。Δ0,Δ1分別為混沌和變異閾值。引入了混沌和變異操作之后，粒子群的多樣性得到了提高。

由上述分析得到的CMCPSO算法的流程

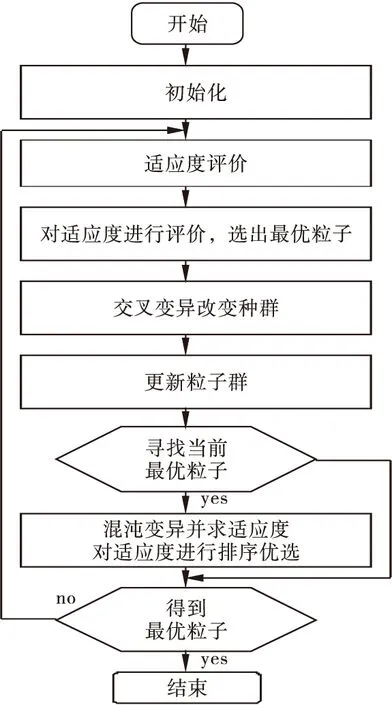
圖1

4 基于CMCPSO的電網規劃

電網規劃優化函數[14]為

式中：第一部分為網絡投資；第二部分為整個網絡的網損；資金回收系數k1=r(1+r)n/[r(1+r)n-1]；cj為支路j中擴展一回新建線路的投資費用；xj為支路j中新建線路回數；Ω1為待選新建線路集合；年網損費用系數k2=Costτ/u2，其中Cost為網損電價，τ為最大負荷損耗時間，u為系統額定電壓；rj為支路j的電阻；Pj為正常情況下支路j輸送的有功功率；Ω1和Ω分別為網絡中已有線路和新建線路的集合。潮流約束條件為

(7)

式中：pi和Qi分別為節點i(i=1～N)的注入有功功率和無功功率；節點i與j之間的相角差θij=θi-θj；N為節點總數。所有節點電壓Ui須滿足

Uimin≤Ui≤Uimax(i∈N)

(8)

所有電源節點的有功功率和無功功率要滿足

(9)

式中：PGi和QGi分別為電源節點i(i∈G)的有功功率和無功功率；G為電源節點集合。所有線路的傳輸功率須滿足

(10)

式中：pi和qi分別為線路i(i∈Ω)的有功功率和無功功率；pimax和qimax分別為線路最大有功功率和無功功率。架線回數須滿足

0≤xi≤ximax且xi∈Ni∈Ω1

(11)

式中：ximax為架線回數最大值；N為非負整數集。電網規劃的決策變量為整數，則粒子位置的向量為

X=[x1,x2,…,xi…xm]

(12)

式中：xi為第i條線路從0到線路走廊所能架設線路回數上限之間的整數；m為系統中可增加線路走廊數。

5 算例分析

IEEE-6節點電網系統是國內外電網規劃研究人員所廣泛采用的試驗電網[1]。本文實證分析也引用IEEE-6節點電網系統。在6個節點中，任意兩個節點之間都可以架設新線，共有15條可架線走廊。其中節點6是新建發電廠，必須聯入電網。假設系統中任意兩節點間的潮流在多回線路上是平均分配的。粒子數取20，學習因子c1和c2均取2，懲罰系數U1取1000，懲罰系數U2取10000。

分別用PSO算法和CMCPSO算法進行運算，結果可見表1。通過表1結果對比，在粒子數為20時，基本PSO在50次優化計算中沒搜索到一次最優，原因是基本PSO一旦找到一個局部最優點，群中粒子容易被吸引到該局部最優區域，喪失了繼續搜索的能力，所以不能得到最優解。而采用本文CMCPSO后，由于引入了混沌序列，幫助那些局部惰性粒子逃脫束縛并快速尋找到最優解。

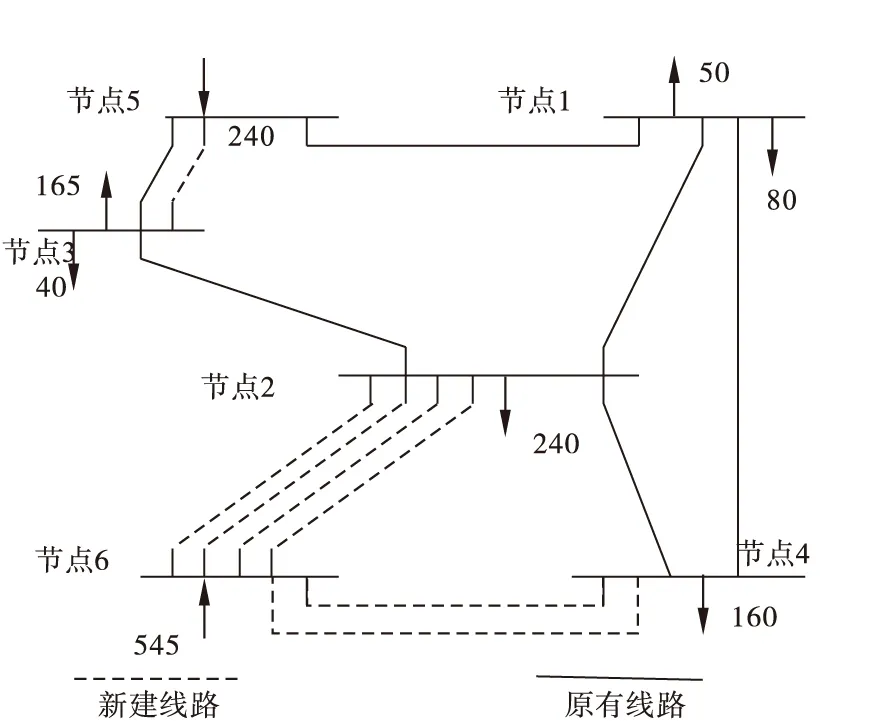
圖2

表1 基本PSO和CMCPSO的比較

6 結論

本文提出的融合交叉變異和混沌的新型粒子群算法，引入了遺傳算法和混沌算法的優化思想。在種群的每帶進化過程中引入了交叉操作，顯著地增加了種群的多樣性，同時提高了種群進化速度。傳統的粒子群算法在迭代后期粒子極易陷入停滯狀態，本文提出的混合算法通過引入混沌擾動或變異操作，雙重保障粒子足以跳出局部極小點，改善了粒子群優化算法擺脫局部極值點的能力，提高了算法全局搜索最優的能力。具體算例結果表明，該算法具有較高的運行效率和全局收斂能力，能夠很好的求解大規模電網規劃優化問題。

[1] 王錫凡.電力系統優化規劃[M].北京：水利電力出版社，1990.

[2] 王秀麗,王錫凡.遺傳算法在輸電系統規劃中的應用 [J].西安交通大學學報，1995，29(8)：1-9，16.

[3] 王秀麗，李淑慧，陳皓勇,等.基于非支配遺傳算法及協同進化算法的多目標多區域電網規劃[J].中國電機工程學報，2006，26(12)：11-15.

[4] 劉方，顏偉，Yu D C.基于遺傳算法和內點法的無功優化混合策略[J].中國電機工程學報，2005，25(15)：67-72.

[5] 翟海保，程浩忠，呂干云,等.基于模式記憶并行蟻群算法的輸電網規劃 [J].中國電機工程學報，2005，25(9)：17-22.

[6] 郝晉，石立寶，周家啟，等.基于蟻群優化算法的機組最優投入[J].電網技術，2002，26(11)：27-32.

[7] 孫薇，商偉，牛東曉.改進蟻群優化算法在配電網網架規劃中的應用[J].電網技術，2006，30(15)：85-90.

[8] 侯云鶴，熊信艮，吳耀武，等.基于廣義蟻群算法的電力系統經濟負荷分配[J].中國電機工程學報，2003，23(3)：59-64.

[9] 陳章潮，顧潔，孫純軍. 改進的混合模擬退火—遺傳算法應用于電網規劃[J].電力系統自動化，1999，23(10)：28-32.

[10] 謝敬東，唐國慶，吳新余.進化規劃在電網規劃中的應用[J].電力系統及其自動化學報，1998，10(2)：15-20.

[11] Clerc M，Kennedy J.The particle swarm：explosion stability and convergence in a multi-dimensional complex space IEEE Trans?? Evolutionary Compute，2002，6(1)：58-73.

[12] Shi Y，Eberhart R C Empirical study of particle swarm optimization//Proceedings of the IEEE Congress on Evolutionary Computation Piscataway，NJ：IEEE Press，1999：1945-1950.

[13] Richards M，Ventura D.Choosing a starting configuration for particle swarm optimization //Proc.IEEE Int.Joint.Conf Neural Netw，2004：2309-2312.

[14] Chung T S，Li K K，Chen G J，et al. Multi-objective transmission network planning by a hybrid GA approach with fuzzy decision analysis[J]. Electrical Power and Energy Systems(S0092-2051)，2003，5(2)：187-192.

[15] 劉朝，祁榮賓,錢鋒.融合交叉變異和混沌的新型混合粒子群算法[J].化工學報，2010，61(11)：2861-2867.

A Novel Hybrid Particle Swarm Optimization Algorithm and Its Application in Transmission Network Expansion Planning

GAOMing，ZHOUHao

(State Grid Turpan Power Supply Company，Turpan 838000，China)

The problem of transmission network planning is a nonlinear integer planning problem with restraint conditions and discrete variables and a difficult and outstanding problem in planning research.A hybrid particle swarm optimization algorithm merging crossover mutation and chaos(CMCPSO) was used into solving the transmission network planning problem.Compared with ordinary particle swarm algorithm,the hybrid particle swarm algorithm can more quickly and effectively to find the optimal solution.At last,the validity and reliability of the method is demonstrated by a case.

transmission network planning；particle swarm optimization；crossover；mutation；chaos

1004-289X(2015)03-0087-04

TM72

B

2014-05-15

高明(1988-)，男，本科，長期從事電力系統規劃工作、電力系統設計工作； 周浩(1985-)，男，本科，長期從事電力系統變電運檢工作。