跨斷層橋梁地震響應(yīng)分析及合理跨越角度研究
惠迎新,王克海,吳 剛,李 沖
(1.東南大學(xué) 交通學(xué)院,南京 210096;2.交通運輸部 公路科學(xué)研究院,北京 100088)
建于活動斷層區(qū)域的建筑結(jié)構(gòu)地震時具有較大的破壞風(fēng)險。為此,國內(nèi)外抗震規(guī)范提出了相關(guān)規(guī)定或建議予以規(guī)避,如禁止在活動斷層之上新建結(jié)構(gòu)物或要求與活動斷層之間設(shè)置一定的避讓距離。然而對于跨越峽谷、河流等障礙物的橋梁結(jié)構(gòu),由于地形地貌、建設(shè)成本、工程周期等各種客觀條件的限制,往往難以遵循這些原則。在1999年集集地震、1999年土耳其Kocaeli地震與 Duzce地震及 2008 年汶川地中[1-4],二十余座橋梁因活動斷層穿過而發(fā)生嚴(yán)重破壞或全橋垮塌,造成嚴(yán)重?fù)p失。
上述地震中出現(xiàn)的問題顯露出目前抗震研究工作的不足和局限性,對跨斷層橋梁結(jié)構(gòu)如何避免或減輕結(jié)構(gòu)損毀是今后抗震研究面臨的新課題。目前針對跨斷層橋梁的相關(guān)研究工作尚處于初始階段,僅有少量國外學(xué)者對此進(jìn)行了研究,在我國,該領(lǐng)域的研究工作基本處于空白狀態(tài)。美國學(xué)者Bray等[5]通過對震后“幸存”的跨斷層結(jié)構(gòu)物進(jìn)行分析,提出了不是所有的活動斷層都能避讓,也不是所有活動斷層都需要避讓的觀點。Park等[6]對土耳其Duzce地震中發(fā)生嚴(yán)重破壞的跨斷層橋梁bolu 1號高架橋的抗震性能進(jìn)行了分析,認(rèn)為設(shè)計之初對可能出現(xiàn)的斷層錯動考慮不充分,也是地震中橋梁嚴(yán)重?fù)p毀的重要原因。Goel、Chopra等[7-8]研究了地表斷層破裂區(qū)常規(guī)中小跨直線橋和曲線橋地震響應(yīng)需求的簡化計算方法。上述研究主要從該類橋梁的震害、簡化計算方法等方面進(jìn)行了初步探討,未就其地震響應(yīng)規(guī)律、設(shè)防對策等方面做進(jìn)一步研究。此外,對于跨斷層橋梁應(yīng)采用何種角度跨越活動斷層有利于抗震設(shè)防,國內(nèi)外學(xué)者對此也未有研究。為此,掌握跨斷層橋梁地震響應(yīng)規(guī)律,探討橋梁與活動斷層最佳交角,對該類橋梁的抗震設(shè)防具有重要意義。
本文以一座跨越走滑斷層的連續(xù)梁橋為例,采用混合模擬法合成了跨斷層橋梁地面運動時程曲線,通過有限元模擬方法對跨斷層橋梁在地震動作用下的結(jié)構(gòu)響應(yīng)規(guī)律開展研究,分析了橋梁結(jié)構(gòu)跨越走滑斷層的最佳交角,為實際工程中跨斷層橋梁的抗震設(shè)計與合理橋位布置提供參考和依據(jù)。
1 工程概況
依托工程為3×30 m預(yù)應(yīng)力混凝土連續(xù)梁橋(見圖1),主梁采用單箱單室箱梁截面,梁高1.8 m。由于受到路線總體規(guī)劃、地形地貌等多方面客觀條件的限制,不得不采用橋梁形式跨越活動斷層,跨斷層橋跨為該橋第二跨。所跨活動斷層為具有左旋分量的走滑斷層,斷裂走向與橋位基本垂直(見圖2)。依據(jù)地質(zhì)構(gòu)造條件,歷史地震等地震安評資料,橋址區(qū)域潛在震級上限為7.5級,最大水平錯距1.5 m,場地類別為Ⅱ類。該橋支座采用鉛芯橡膠支座;橋墩為2.2 m×5 m矩形橋墩,墩高在10~11 m之間,計算時取11 m;樁基采用鉆孔灌注樁。
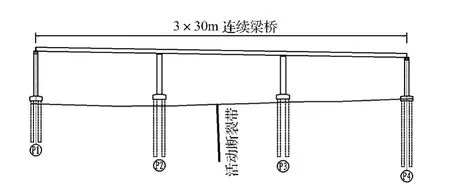
圖1 橋型布置圖Fig.1 The layout of the bridge

圖2 橋位與斷層關(guān)系示意圖Fig.2 Location between the bridge and the fault
2 地面運動模擬
跨斷層橋梁的地面運動是地震動中最為復(fù)雜的一種,主要表現(xiàn)為斷層破裂方向性效應(yīng)和靜態(tài)滑沖效應(yīng)引起的脈沖型地面運動。其中,破裂方向性效應(yīng)以大幅值、長周期、短持時的強速度脈沖為主要特征;滑沖效應(yīng)是由斷層兩側(cè)相對錯動引起的,以位移時程突然升高或降低形成地面永久位移為主要特征。對于走滑斷層,方向性速度脈沖和滑沖效應(yīng)速度脈沖出現(xiàn)在不同的地震動分量上,其中方向性脈沖表現(xiàn)在垂直于斷層分量(Fault-Normal),滑沖效應(yīng)速度脈沖表現(xiàn)在平行于斷層分量(Fault-Parallel)。通常垂直于斷層方向的方向性效應(yīng)和平行于斷層方向的滑沖效應(yīng)幾乎同時發(fā)生,應(yīng)同時予以考慮[9]。
根據(jù) Mavroeidis,田玉基等[10-11]對速度脈沖型地震記錄的統(tǒng)計,速度脈沖周期通常大于1 s,即速度脈沖是小于1 Hz的低頻成分。因此在短周期(高頻),等效脈沖加速度反應(yīng)譜與實際地震記錄的加速度反應(yīng)譜不符。針對這種情況,在模擬跨斷層地面運動時程時,應(yīng)分別模擬大于1 Hz的高頻部分與小于1 Hz的低頻脈沖部分(破裂方向性效應(yīng)和滑沖效應(yīng)),然后將二者進(jìn)行疊加合成包含多種頻率成分并且能夠反映跨斷層地面運動特點的地震動時程。其中,高頻部分(>1 Hz)采用 Thráinsson 等[12]提出的基于相位差譜的人工地震動合成法模擬,低頻脈沖部分(<1 Hz)的方向性效應(yīng)速度脈沖和滑沖效應(yīng)速度脈沖分別采用Makris等[13]提出雙半波速度脈沖模型和單半波速度脈沖模型模擬。滑沖效應(yīng)引起的斷層兩側(cè)地面相對錯動,采用大小相同、方向相反的地震動時程以模擬斷層相對錯動。
依據(jù)橋址處的場地條件、潛在矩震級以及水平錯距等地震安評資料,由 Somerville[14-15]提出的脈沖周期T與震級Mw的統(tǒng)計公式以及脈沖峰值Vp與震級Mw、斷層距R的統(tǒng)計公式可得到 T=3.75 s,Vp=153 cm/s。通過隨機指定初相位角隨機生成三條高頻時程分量,并與相應(yīng)低頻時程疊加,獲得三組垂直于斷層方向和平行于斷層方向的加速度、速度和位移時程,地震動豎向分量可采用高頻時程模擬,三組三分量位移時程分別命名為KD1、KD2和KD3。限于篇幅,圖3僅給出一組(KD1)模擬合成的斷層兩側(cè)水平地面運動時程。
圖4(a)、(b)、(c)分別為阻尼比為5%時,KD1在垂直于斷層方向(FN)、平行斷于斷層方向(FP)和豎直方向(V)上的彈性加速度、速度和位移反應(yīng)譜。由圖4可知,加速度、速度和位移反應(yīng)譜,在短周期各向分量差別不大;越接近脈沖周期(T=3.75 s)各向分量差別越大。垂直斷層方向的速度譜顯著大于平行斷層方向,其速度譜峰值發(fā)生于脈沖周期附近,這與Somerville等[9]對斷層地表破裂地震動特性的研究成果一致。
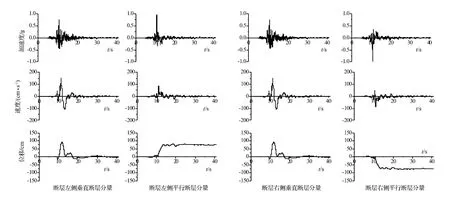
圖3 斷層兩側(cè)垂直斷層方向和平行斷層方向加速度、速度和位移時程Fig.3 Acceleration,velocity and displacement time histories of fault- normal and fault- parallel components
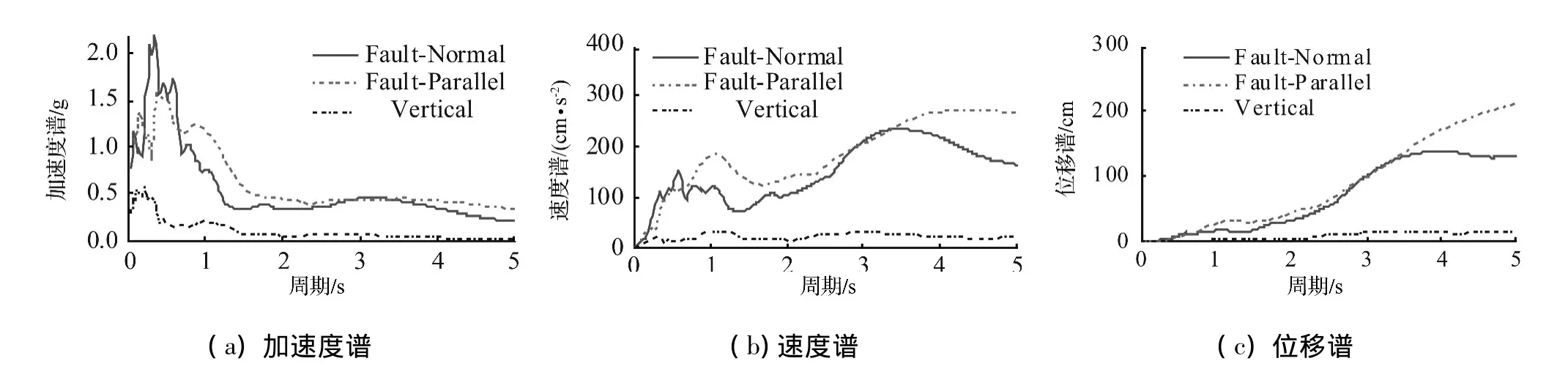
圖4 地震動反應(yīng)譜Fig.4 Response spectra in three components
3 跨斷層橋梁地震響應(yīng)分析
3.1 模型建立與地震動輸入
采用加州大學(xué)伯克利分校開發(fā)的結(jié)構(gòu)分析程序OpenSees對算例橋梁進(jìn)行有限元建模及分析,有限元離散模型如圖5所示。主梁和橋墩采用三維線性梁柱單元模擬,樁土相互作用采用承臺底加6個自由度的彈簧模擬。每個橋墩墩頂布置兩個鉛芯橡膠支座(LRB),支座型號為 J4Q 870×870×289 G0.8型,水平向恢復(fù)力模型采用雙向恢復(fù)力-位移滯回模型模擬,屈服前剛度K1、屈服后剛度 K2按規(guī)范[16]取值,計算時不計支座轉(zhuǎn)動剛度,豎向剛度KV及扭轉(zhuǎn)剛度KZ參照文獻(xiàn)[17]計算。為考慮平行于斷層方向的非一致地面運動及永久地面位移,地震動輸入采用多點激勵位移輸入模型[18],并將上節(jié)模擬合成的三組三分量位移時程作為斷層兩側(cè)橋墩的地震動輸入。圖6為地震動輸入方向平面示意圖,F(xiàn)N、FP、V分別代表垂直于斷層分量、平行斷于斷層分量和豎向分量。在FN和V分量,斷層兩側(cè)橋墩地震動激勵相同,地震動輸入為空間一致激勵;在FP分量,斷層兩側(cè)橋墩采用大小相同、方向相反的地震動時程以模擬斷層相對錯動,地震動輸入方式為空間非一致激勵。非線性動力時程分析采用Newmark-β 直接積分法,其中 α =0.5、β =0.25。
3.2 內(nèi)力響應(yīng)分析
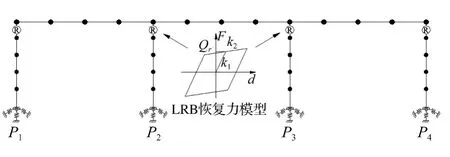
圖5 有限元離散模型Fig.5 Finite element discretization model of the bridge
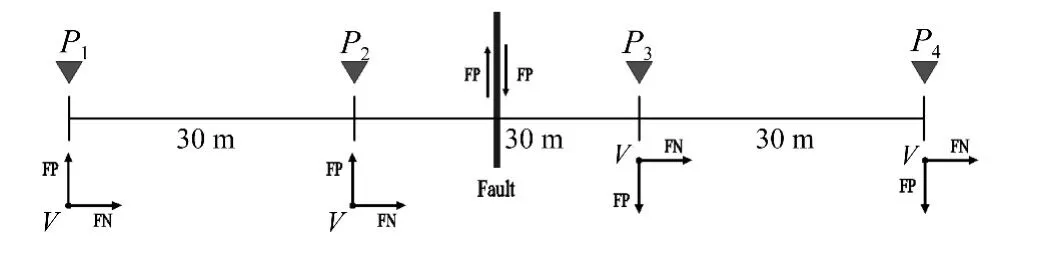
圖6 地震動輸入方向示意圖Fig.6 Schematic of ground motion input direction
在KD1、KD2、KD3地震動作用下,各墩墩底最不利彎矩和扭矩如表1所示。由表1可知,三組地震動作用下,P1墩~P4墩內(nèi)力分布規(guī)律相似,內(nèi)力響應(yīng)值差別不明顯,說明高頻時程對橋墩內(nèi)力響應(yīng)峰值影響有限,低頻脈沖效應(yīng)主導(dǎo)橋墩內(nèi)力設(shè)計值。在縱橋向,P1墩~P4墩縱向彎矩較為接近,這是因為該橋下部結(jié)構(gòu)剛度相同,各墩均采用鉛芯橡膠支座而未設(shè)置固定墩,因而分配給各墩的地震力基本相同;同時也說明活動斷層垂直穿過橋梁時,斷層相對錯動對縱橋向地震響應(yīng)影響較小。在橫橋向,距斷層較近的P2、P3墩彎矩較P1、P4墩大,平均差值接近25%。值得注意的是,跨斷層橋梁各墩均承受了較大的扭矩,扭矩平均值接近50000 kN·m,而通常在常規(guī)近場、遠(yuǎn)場地震作用下橋墩扭矩較小,基本可忽略不計。這主要是因為斷層錯動時斷層兩側(cè)橋墩運動方向不同,主梁面內(nèi)較大的彎曲剛度以及支座的抗扭剛度,對橋墩扭轉(zhuǎn)具有較強約束作用,從而引起了橋墩的較大扭矩。在1999年土耳其Duzce地震中,活動斷層穿過Bolu 1號高架橋,斷層錯動導(dǎo)致其右幅橋45號墩與左幅橋47號墩發(fā)生約12°的扭轉(zhuǎn)變形[2]。因此,在對跨斷層橋梁進(jìn)行設(shè)計時,應(yīng)對墩柱的抗扭設(shè)計予以重視,可采用抗扭剛度較大的橋墩形式,以抵抗斷層相對位移產(chǎn)生的較大剪力和扭矩。

表1 橋墩墩底內(nèi)力響應(yīng)結(jié)果Tab.1 Internal force calculating results for pier bottom (Unit:kN.m)
3.3 位移響應(yīng)分析
KD1、KD2、KD3地震動作用下,P1墩 ~P4墩主梁最大相對位移如表2所示。主梁相對位移為主梁梁底相對與橋墩墩頂?shù)奈灰疲布创砹酥ё到y(tǒng)的位移響應(yīng)。由表2可知,在縱橋向,P1墩~P4墩墩頂主梁最大縱向相對位移值相同,在KD3作用下,邊墩(P1墩)最大值達(dá)54.5 cm。在橫橋向,斷層兩側(cè)橋墩的位移響應(yīng)值大小相同,方向相反,主梁將產(chǎn)生較大的平面內(nèi)扭轉(zhuǎn)變形。此外,非線性時程計算結(jié)果表明,斷層錯動發(fā)生后,支座和橋墩在縱橫向均產(chǎn)生了一定的殘余位移,其中橫橋向殘余位移較為顯著。橋墩殘余位移為地震動結(jié)束后墩頂節(jié)點相對于墩底節(jié)點的位移。支座及橋墩墩身橫向位移響應(yīng)時程分別如圖7和圖8所示(以KD1為例),該特征與土耳其地震、臺灣集集地震跨斷層橋梁震害描述一致[4]。KD1、KD2、KD3地震動作用下,P1墩~P4墩支座殘余位移、橋墩殘余位移值列于表2。綜合以上分析可得,跨斷層橋梁位移響應(yīng)以主梁縱橫向大位移、面內(nèi)扭轉(zhuǎn)變形以及支座和橋墩殘余位移為主要特征,具有較大的落梁破壞風(fēng)險。
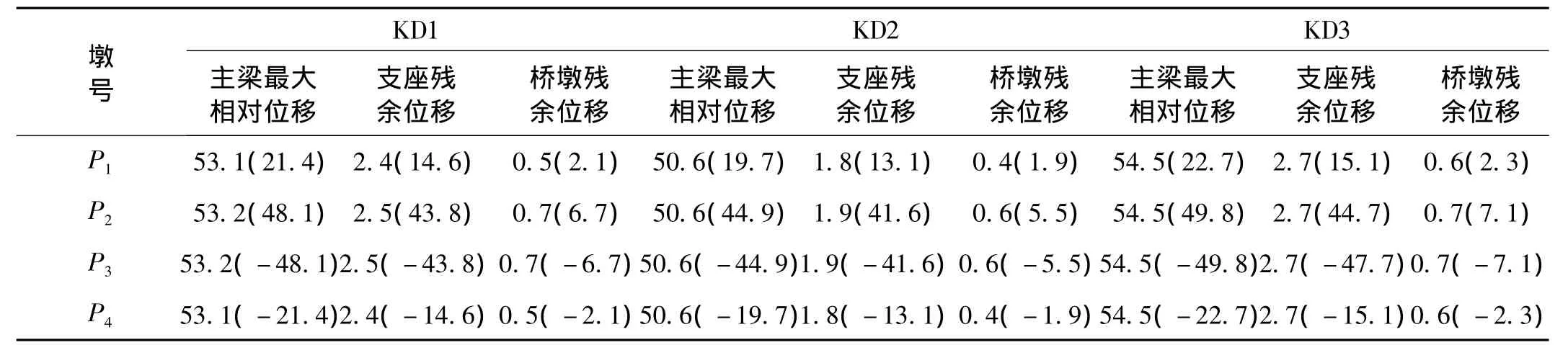
表2 位移響應(yīng)計算結(jié)果Tab.2 Displacement response calculating results

圖7 支座橫向滯回曲線Fig.7 Transverse force-displacement relationship of LRB
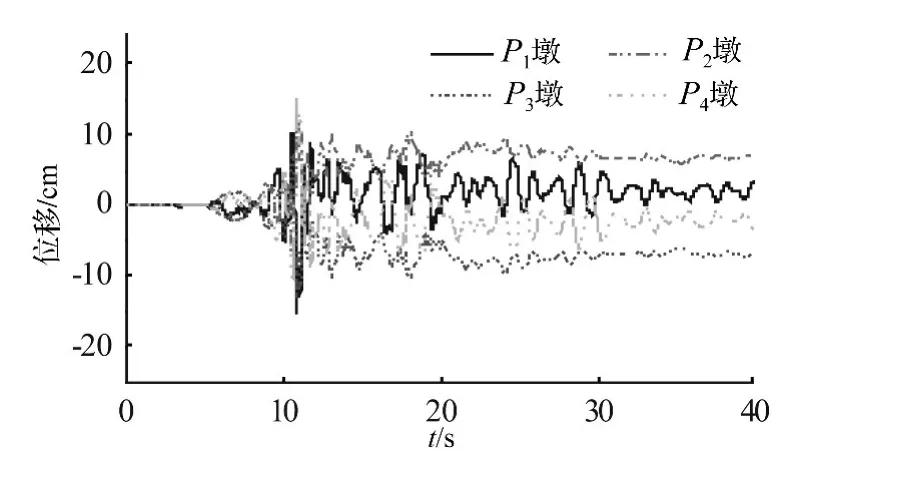
圖8 橋墩墩身橫向位移時程Fig.8 Transverse relative displacement time history of pier
4 橋梁與活動斷層最佳交角分析
為研究不同跨越活動斷層角度對橋梁結(jié)構(gòu)地震響應(yīng)的影響,選取橋梁軸向與斷層交角θ為計算參數(shù),對三組地震動作用下,θ在15°~165°之間(以15°為間隔)共計33個計算工況(3×11)進(jìn)行三維非線性時程分析,計算示意如圖9所示,θ角以逆時針旋轉(zhuǎn)為正。計算時將斷層兩側(cè)垂直斷層分量(FN)和平行斷層分量(FP)的地震動時程按圖10所示轉(zhuǎn)換為縱橋向(L)和橫橋向(T)地震動時程進(jìn)行輸入,轉(zhuǎn)換公式見式(1)。內(nèi)力和位移計算結(jié)果取KD1、KD2、KD3響應(yīng)平均值。
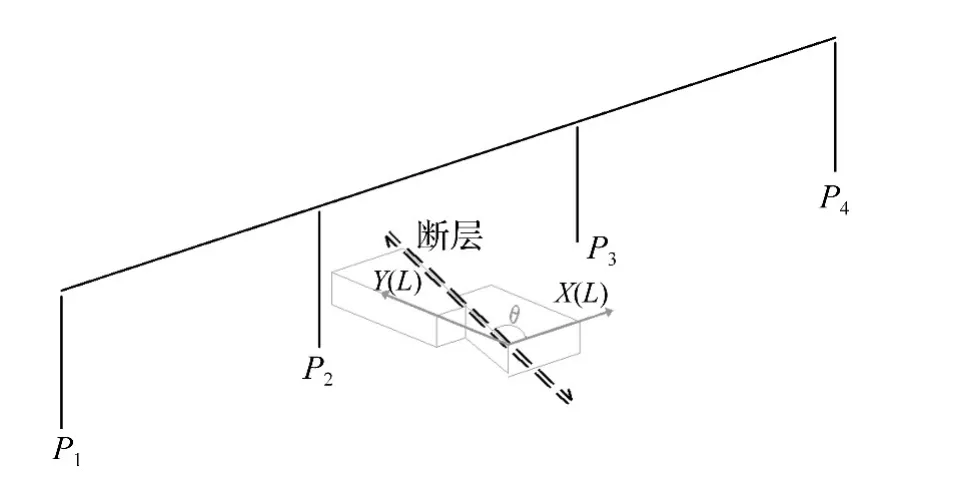
圖9 不同斷層交角計算模型Fig.9 Calculation model of different fault crossing Angle
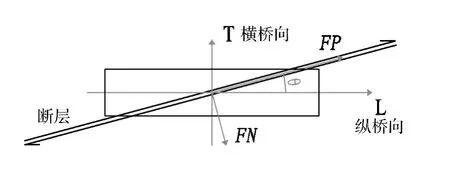
圖10 地震動轉(zhuǎn)換示意圖Fig.10 Schematic of ground motion transformation
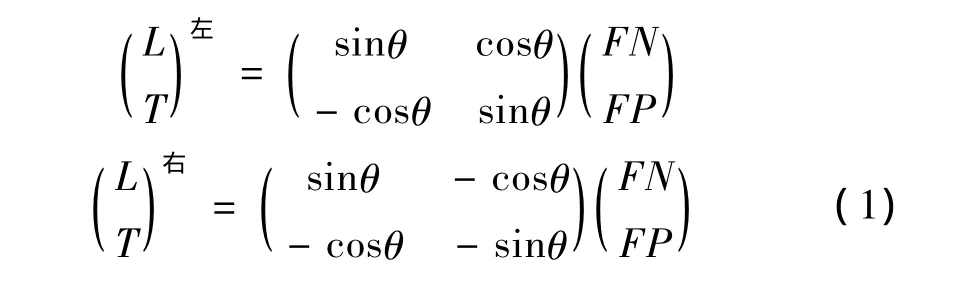
4.1 斷層交角對內(nèi)力響應(yīng)的影響
經(jīng)建立不同斷層交角模型分析,P1墩~P4墩墩底最不利彎矩、扭矩隨斷層與橋軸向交角θ的變化情況如圖11所示。
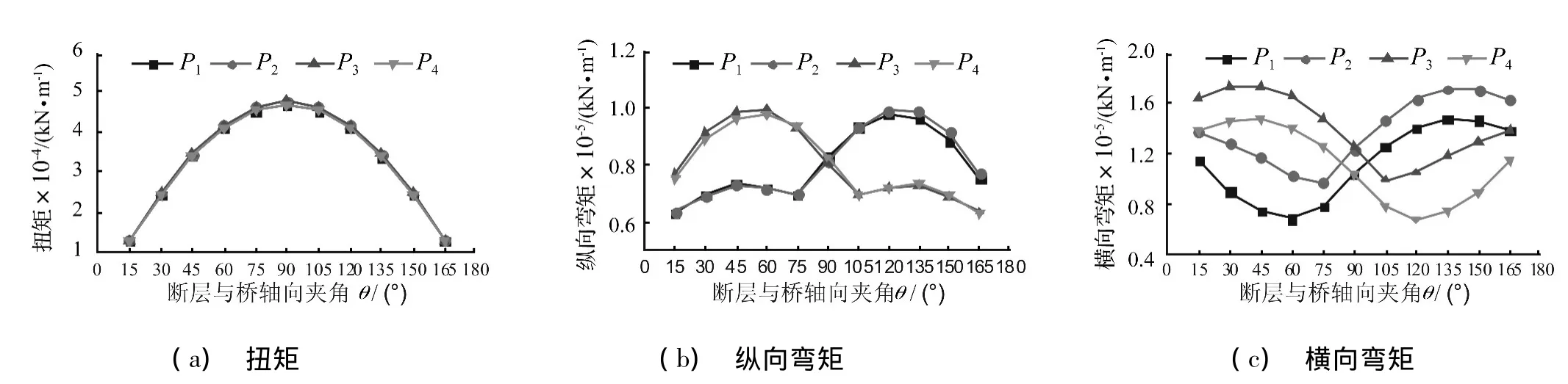
圖11 墩底最不利彎(扭)矩隨斷層交角變化曲線Fig.11 Unfavorable value of pier base moment and torque
由圖11可知,斷層左側(cè)P1墩、P2墩墩底彎矩、扭矩值,以θ=90°為對稱軸,分別與斷層右側(cè)P4墩、P3墩對稱相等。由圖11(a)可知,最不利扭矩隨斷層交角θ的增大呈先增大后減小趨勢,θ=90°時扭矩最大。由圖11(b)和圖11(c)可知,當(dāng)θ=90°時,P1墩~P4墩縱橋向彎矩基本相等,其設(shè)計值約為80000 kN·m,此時斷層錯動對橋墩縱向彎矩分布影響最小。在橫橋向,距斷層較近的P2墩和P3墩彎矩大于P1墩和P4墩,其橫向彎矩設(shè)計值約為125000 kN·m。由圖11(c)還可觀察到,其它θ角對應(yīng)的橫向彎矩分布與θ=90°時具有相似規(guī)律,說明跨斷層橋梁橋墩橫向彎矩響應(yīng)值隨斷層距離的減小而增加。當(dāng)θ在(30°,90°)范圍內(nèi),P1墩、P2墩縱橫向彎矩值相對較小,此時P3墩彎矩控制設(shè)計,當(dāng)θ在45°附近時其值最大,縱橫向彎矩設(shè)計值分別約為100000 kN·m和180000 kN·m,較θ=90°時的設(shè)計彎矩值大25%和45%;而當(dāng) θ在(90°,160°)范圍內(nèi),則P2墩彎矩為控制彎矩,θ在135°附近時設(shè)計彎矩值最大。當(dāng)θ=15°或θ=175°時,其縱向設(shè)計彎矩雖然較θ=90°小6%,但其橫向設(shè)計彎矩較θ=90°大 34%。
綜合以上分析可知,當(dāng)θ=90°時,橋墩縱橫向彎矩分布合理,設(shè)計值總體小于其它工況。因此,在滿足橋墩抗扭強度的條件下,斷層與橋軸向交角θ為90°,即橋梁垂直跨越活動斷層時,橋墩受力合理性和經(jīng)濟性最優(yōu)。
4.2 斷層交角對位移響應(yīng)的影響
與內(nèi)力響應(yīng)規(guī)律相同,P1墩、P2墩位移響應(yīng)分別與P4墩、P3墩對稱相等,鑒于篇幅,位移響應(yīng)分析中僅列出P1墩和P2墩的計算結(jié)果。P1墩和P2墩主梁相對位移、支座殘余位移、橋墩殘余位移隨斷層與橋軸向交角θ的變化情況分別如圖12(a)、(b)、(c)所示。
由圖12可知,P1墩與P2墩的縱向位移響應(yīng)隨斷層交角θ的變化規(guī)律和數(shù)值相同,總體呈先減小后增大的變化趨勢,在θ=90°時主梁相對位移、支座殘余位移、橋墩縱向位移均為最小值,其值分別為相應(yīng)位移響應(yīng)最大值的68%、4%和0.5%。由此可知,當(dāng)橋梁非垂直跨越活動斷層時,平行于斷層方向(FP)的斷層錯動會增加結(jié)構(gòu)縱向位移響應(yīng),且其響應(yīng)值隨斷層與橋梁軸線正交方向偏離程度的增加而增加。
在橫橋向,P1墩與P2墩的位移響應(yīng)隨斷層交角θ的變化規(guī)律相似,但P2墩位移響應(yīng)值較P1墩大。當(dāng)θ=90°時,主梁橫向相對位移為最小值(圖12(a)),而支座橫向殘余位移(圖12(b))、橋墩橫向殘余位移(圖12(c))為最大值,但其值與相應(yīng)縱向響應(yīng)值相比較小,分別為支座縱向殘余位移和橋墩縱向殘余位移最大值的70%和41%。此外,文獻(xiàn)[4]對跨斷層橋梁的震害統(tǒng)計表明,該類橋梁的落梁破壞方向均為縱橋向。因此,綜合以上分析可知,跨斷層橋梁防落設(shè)計的重點為縱橋向,為減小斷層錯動產(chǎn)生的順橋向位移分量,降低落梁風(fēng)險,橋梁應(yīng)垂直跨越活動斷層。
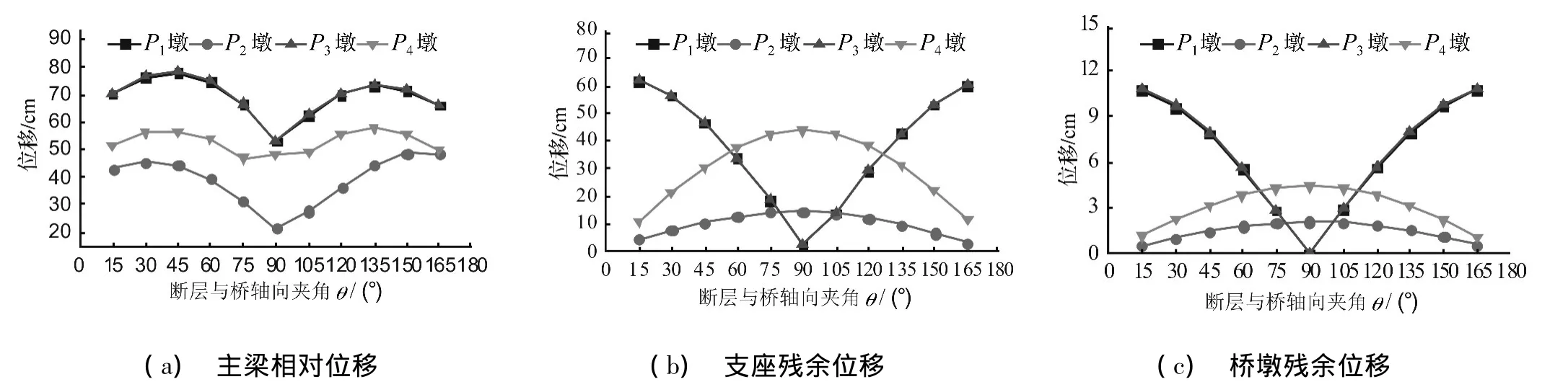
圖12 P1墩和P2墩最不利位移響應(yīng)隨斷層交角變化曲線Fig.12 Unfavorable value of displacement response at P1 and P2
5 結(jié)論
本文以一座三跨連續(xù)梁橋為研究對象,采用非線性時程分析方法對跨走滑斷層橋梁地震反應(yīng)規(guī)律進(jìn)行了分析,主要結(jié)論為:
(1)跨斷層橋梁橋墩扭矩設(shè)計值較大,橋墩橫向彎矩隨斷層距的減小而增加。
(2)跨斷層橋梁位移響應(yīng)以主梁縱橫向大位移、面內(nèi)扭轉(zhuǎn)變形、支座和橋墩殘余位移為主要特征,具有較大的落梁破壞風(fēng)險,設(shè)計時應(yīng)對該類橋梁的防落梁措施進(jìn)行專項研究。
(3)橋梁垂直跨越活動斷層穿時(θ=90°),橋墩受力合理性和經(jīng)濟性最優(yōu),斷層錯動產(chǎn)生的順橋向位移分量最小,落梁風(fēng)險相對較低。
[1]Lu C H,Liu K Y,Chang K C.Seismic performance of bridges with rubber bearings:lessons learnt from the 1999 Chi-Chi Taivan earthguake[J].Journal of the Chinese Institute of Engieers,2011,34(7):889 -904.
[2]Erdik M,Aydinoglu N,Uckan E,et al.The 1999 Turkey earthquakes:Bridge performance and remedial actions[M].Oakland,CA.:Earthquake Engineering Research Institute Publication,2003.
[3]陳樂生,莊衛(wèi)林,趙河清,等.汶川地震公路震害調(diào)-橋梁[M].北京:人民交通出版社,2012.
[4]惠迎新,王克海,李沖.跨斷層地表破裂帶橋梁震害研究及抗震概念設(shè)計[J].公路交通科技,2014,31(10):145-151.HUI Ying-xin,WANG Ke-hai,LI Chong.Study of seismic damage and seismic conceptual design of bridges crossing fault-rupture zones[J]. Journal of Highway and Transportation Research and Development,2014,31(10):145-151.
[5]Bray J D.Designing buildings to accommodate earthquake surface fault rupture[R].USA:ATC &SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures,2009:1 -12.
[6]Park S W,Ghasemi H,Shen J,et al.Simulation of the seismic performanceof the bolu viaduct subjected to near-fault ground motions[J].Earthquake Engineering and Structural Dynamics,2004,33:1249 -1270.
[7]Goel R K,Chopra A K.Linear analysis of ordinary bridges crossing fault-rupture zones[J]. Journal of Bridge Engineering,2009,14(3):203 -215.
[8]Rakesh Goel,Bing Qu,Jennifer Tures,et al.Validation of fault rupture-response spectrum analysis method for curved bridges crossing strike-slip fault rupture aones[J].Journal of Bridge Engineering,2014,19(5).
[9]Somerville P,Characterizing near fault ground motionfor the design and evaluation of bridges[C].Proceedings of the 3rd National Seismic Conference and Workshop on Bridges and Highways,Portland,Oregon,2002:137 -148.
[10]Mavroeidis G P, Papageorgiou A S. A mathematical representationof near-fault ground motions[J].Bull Seism Soc Amer,2003,93(3):1099 -1131.
[11]田玉基,楊慶山,盧明奇.近斷層脈沖型地震動的模擬方法[J].地震學(xué)報,2007,29(1):78-84.TIAN Yu-ji, YANG Qing-shan, LU Ming-qi. Simulation method of near-fault pulse-type ground motion[J].ACTA Seismological Sinica,2007,20(1):80-87.
[12]Thráinsson H, Kiremidjian A S. Simulation of digital earthquake accelerograms using the inverse discrete fourier transform[J]. Earthquake Engineering and Structural Dynamics,2002,31:2023 -2048.
[13]Makris N,Chang S P.Effect of viscous,viscoplasticand friction damping on the response of seismic isolated structures[J].Earthquake Engineering and Structural Dynamics,2000,29:85 -107.
[14]Somerville P G.Magnitude scaling of the near-fault rupture directivity pulse[J].Phys Earth Planet Interi,2003,137:201-212.
[15]Somerville P G.Developmentof an improved ground motion representation for near-fault ground motions[C].Proceedings SMIP 98 Seminar on Utilization of Strong Motion Data.Oakland,California:California Division of Mines and Geology,1998:1 -20.
[16]JTT 822-2011公路橋梁鉛芯隔震橡膠支座[S].
[17]Constantinou M C,Whittaker A S,F(xiàn)enz D M,et al.Seismic isolation of bridges[R].Version 2,Report to Sponsor,California Department of Transportation,Sacramento,2007.
[18]田玉基,楊慶山.地震地面運動作用下結(jié)構(gòu)反應(yīng)的分析模型[J].工程力學(xué),2005,22(6):170-174.TIAN Yu-ji,YANG Qing-shan.Analysis models and methods for structural seismic responses[J].Engineering Mechanics,2005,22(6):170-174.

