考慮冰劈效應的裂縫應力強度因子分析

楊 林 李貴祥

(東北林業大學土木工程學院，黑龍江 哈爾濱 150040)

考慮冰劈效應的裂縫應力強度因子分析

楊 林 李貴祥

(東北林業大學土木工程學院，黑龍江 哈爾濱 150040)

根據熱彈性理論將冰劈效應轉化為冰劈荷載，并基于擴展有限元方法(XFEM)，采用ABAQUS有限元分析軟件建立半無限板模型，求解裂縫在冰劈效應下的應力強度因子，同時通過公式計算其應力強度因子的理論解，將兩者進行了對比分析，采用不同的積分區域因子rk，通過J積分算法求解不同深度裂縫應力強度因子，得到rk取值范圍，通過調整網格加密系數，研究了裂縫區域網格加密對于應力強度因子的影響。

冰劈效應，擴展有限元，加密系數，應力強度因子

0 引言

在各工程領域中，構件斷裂是導致各種災難性事故的重要原因，而構件斷裂主要是由于其內部裂縫在外界因素影響下擴展造成的。進入21世紀，計算機技術的迅猛發展以及大型有限元軟件的開發，為裂縫的研究提供了有效途徑。但目前對于裂縫的研究具有一定局限性，傳統有限元研究中一般預先給定平直的擴展路徑，裂縫只能沿單元邊界擴展，與實際裂縫擴展有較大差距。為改善傳統有限元在裂縫模擬中的局限性，由Belytschko和Black提出了一種新方法，經Moёs和Daux等人完善后正式命名為擴展有限元法[1，2](extended finite element method，XFEM)。該方法比較明顯的優勢是允許裂紋在單元內部擴展，從而實現不規則裂縫的模擬[3]。目前對于裂縫擴展的研究一般集中在荷載和溫度等作用條件上，對于冰劈作用對裂縫擴展的影響研究相對較少。但冰劈效應在實際工程中比較常見，尤其是北方道路路面裂縫積水結冰對路面結構造成嚴重損壞[4]。本文基于擴展有限元法，采用J積分對冰劈效應下裂縫的應力強度因子進行計算和分析。

1 擴展有限元法

擴展有限元法是以單位分解法為基礎，通過在常規有限元位移模式中加入加強函數，來解決不連續問題的一種方法。

1.1 單位分解法

單位分解法(Partition of Unity Method，PUM)是Melenk和Bubska等人于1996年前后提出的一種通過分片來逼近局部的函數[5]。其基本原理是任意函數ψ(x)在求解域Ω中都能用下列形式表示：

(1)

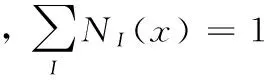
(2)

擴展有限元對式(2)進行擴充來更準確描述復雜未知場，擴充后的未知場uh典型形式為:

(3)

其中，qJ為待定系數，用于調整函數Φ(x)的幅值。

1.2 控制方程

等同于傳統有限元，擴展有限元控制方程根據虛功原理進行推導[6]，假設結構產生的虛位移δuh，則其虛功方程用下式表示：

(4)

其中,Fb為體力;Fs為面力;F為集中力;D為彈性矩陣;ε(u)為應變。

將常規有限元逼近位移函數代入式(4)得到擴展有限元控制方程：

Kδ=R

(5)

其中，K為單元矩陣集合而成的整體勁度矩陣；R為由單元荷載陣列組成的整體陣列；δ為結點未知向量。

1.3 應力強度因子計算

裂縫尖端會發生應力奇異，給數學計算帶來困難，為此引入了描述場強的物理參數應力強度因子(SIF，K)，它的計算依賴于裂縫尖端的局部應力場，是斷裂力學中的重要參數。目前對于Ⅰ型裂縫的應力強度因子KⅠ的計算有直接積分法、J積分和虛擬裂紋閉合法(VCCT)等方法[7]。本文采用精度較高的J積分法進行應力強度因子計算[8,9]。

在ABAQUS中加入用戶程序插件，將以裂縫尖端為圓心半徑為R的區域作為積分區域。

(6)

其中，rk為積分區域因子；h為裂縫尖端所在單元的面積。

通過積分區域因子對積分面積進行控制，將采用不同rk值計算的KⅠ值與理論值進行對比，得到合適的rk值，其示意圖見圖1。

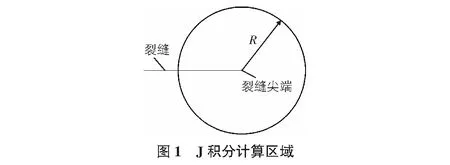
2 裂縫模型的建立與分析

本文主要研究冰劈效應對裂縫的影響，冰劈效應可以轉化為冰劈荷載，并將其視為垂直于裂縫表面的均布壓力，其破壞形式屬于Ⅰ型裂縫。

2.1 冰劈荷載計算

根據熱彈性理論，由冰脹力引起的主應變為：

(7)

其中，εi(i=1,2,3)為3個方向的主應變；Eice為冰的彈性模量；vice為冰的泊松比；p(T)為冰劈荷載。

由文獻[10]可知p(T)引起冰的體積應變為:

(8)

由物理學知識可知冰的體積膨脹系數為：

β(T)=0.000 3e0.044T

(9)

由體積膨脹系數定義可知εv(T)=β(T)，代入式(8)和式(9)可求得冰劈荷載：

(10)

將T=10 ℃，Eice=2 300 MPa，vice=0.35代入式(10)得p(T)=1.190 4 MPa。

2.2 建立有限元模型

采用ABAQUS有限元軟件建立尺寸為4 m×8 m的半無限板模型，板的物理常量為：E=30 MPa，v=0.33，裂縫內充滿水時受力如圖2所示。

為研究不同深度裂縫在劈裂效應下的應力強度因子，本文共建立2 cm，4 cm，6 cm，8 cm，10 cm，12 cm和14 cm深度裂縫模型進行分析計算。如圖3所示為6 cm深度裂縫模型計算結果。

2.3 積分區域因子對比分析

根據應力強度因子手冊，半無限板邊緣裂縫上下表面受到均布壓力p，應力強度因子計算公式為：

(11)

其中,a為裂縫深度;a-b為荷載作用區域，如圖4所示，F(b/a)取值查應力強度因子手冊。

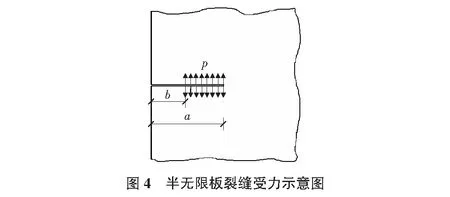
每種裂縫深度模型分別取rk=1.0～4.0計算應力強度因子。應力強度因子理論解通過式(11)代入相關數據進行計算。將兩者進行對比分析，其中有效對比數據為rk=1.5，rk=2.0，rk=2.5，rk=3.0，與理論計算值對比結果如圖5所示。

由圖5可知應力強度因子隨裂縫深度增加而增加，當rk=2.0和rk=2.5時模擬解與理論解吻合度較高，所以建議積分區域因子取2.0～2.5。

2.4 網格密度影響分析

常規有限元模擬裂縫時需要進行網格加密，合適的網格密度是保證準確模擬結果的重要條件。為研究擴展有限元中網格密度對裂縫模擬結果的影響，本文定義網格加密系數Krat，其含義為單位面積網格加密區域包含單元數量Ksc與未加密區域單元數量Kor比值，計算公式如下：

(12)

選取8 cm和10 cm深度的裂縫進行分析，模型為202×100的有限元網格，在此基礎上對裂縫區域進行加密，取rk=2.5。

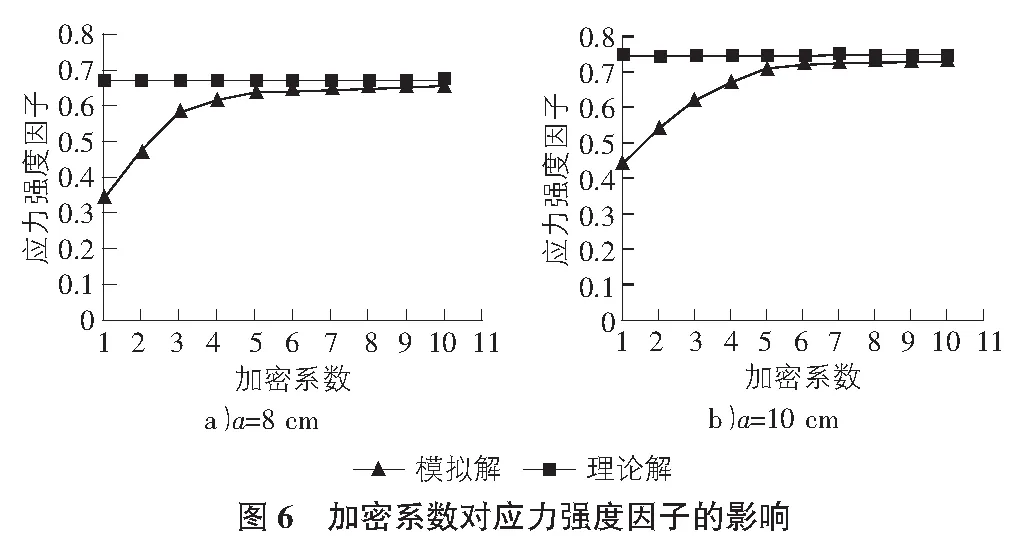
分別計算其應力強度因子值，并與理論值進行對比，結果如圖6所示。由圖6可知模擬數值解隨加密系數的增加逐漸逼近理論解。

2.5 冰劈作用深度影響分析

選取8 cm和10 cm兩種深度的裂縫，建立不同積水深度模型進行分析，通過冰劈荷載的作用范圍對積水深度進行表征。

通過用戶程序插件取rk=2.5計算應力強度因子值與理論計算值進行比較，如圖7所示。

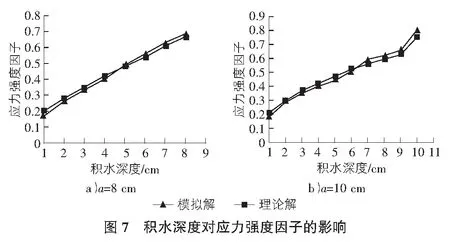
由圖7可知，應力強度因子值隨積水深度的增加而增大，積水深度對應力強度因子影響顯著。積分區域因子rk=2.5時擴展有限元對于裂縫應力強度因子的計算具有較高精度。

3 結語

1)冰劈效應是工程領域研究的重點之一，尤其是季凍區造成工程構造物破壞的重要原因。本文通過將冰劈效應轉換為冰劈荷載，基于擴展有限元的方法，對冰劈效應對裂縫的影響進行了研究。研究表明，擴展有限元對于冰劈荷載下應力強度因子的計算具有較高精度。2)利用ABAQUS用戶程序插件，應用J積分的計算方法對不同深度裂縫應力強度因子進行計算，結果表明，對于半無限板邊緣裂縫模擬，積分區域因子取rk=2.0～2.5計算精度較高。3)對不同加密系數的裂縫模型進行應力強度因子計算表明，加密系數Krat越大，求解精度越高。所以在應用擴展有限元求解裂縫應力強度因子時，對裂縫區域進行適當加密，可提高模擬精度。

[1] Belytschk T, Black T. Elastic crack growth in finite element with minimal remeshing[J].International journal for Numerical Methods in Enginerring,1999(45):601-620.

[2] Moёs N, Dolbw J, Beiytschko T. A finite element method for cracking growth without remeshing[J].International Journal for Numerical Methods in Enginering,1999(46):131-150.

[3] 方修君,金 峰.基于ABAQUS平臺的擴展有限元法[J].工程力學,2007,24(7):6-10.

[4] 趙巖荊,倪富健.冰劈效應對瀝青路面表面裂縫的影響性分析[J].公路交通科技,2011(4):24-30.

[5] Melenk J M, Bubska I. The partition of the nuity finite element method:basic theory and applications[J].Computer methods in Applied Mechanics and Engineering,1996,139(14):289-314.

[6] 魏 翔.基于ABAQUS的混凝土結構非線性有限元分析[J].山西建筑,2011,37(2):32-34.

[7] 祝云琪,曾四平.RCC—AC復合式路面反射裂縫應力強度因子的有限元分析[J].公路工程,2008(4):51-53,74.

[8] 羅 睿,黃曉明.瀝青路面表面裂縫應力強度因子計算方法研究[J].公路交通科技,2002(1):12-15.

[9] 彭 璞,佘滿漢.基于XFEM的瀝青加鋪層材料的裂縫擴展[J].公路工程,2012(4):201-206.

[10] 李云鵬,王芝銀.花崗巖低溫強度參數與冰脹力的關系研究[J].巖石力學與工程學報,2010(S2):4113-4118.

Analysis on cracking stress-intensity factors by considering frost-splitting effect

Yang Lin Li Guixiang

(CollegeofCivilEngineering,NortheastUniversityofForestry,Harbin150040,China)

The paper converts frost-splitting effect into frost-splitting load according to thermal-magnetoelasticity, establishes semi-infinite model by applying ABAQUS finite element analysis software according to XFEM. The cracking stress-intensity factors are solved under frost-splitting effect. Simultaneously, it calculates theoretical stress-intensity factors with calculation, and makes a comparison. And then, it adopts different integral area factorrk, solves various-depth cracking stress-intensity factors by J integral computation method, obtainsrkvaluing scope. Through adjusting grid coefficients encryption, it studies the impact of grid coefficients encryption within cracking area upon stress-intensity factors.

frost-splitting effect, extended finite element method(XFEM), coefficients encryption, stress-intensity factors

2015-05-25

楊 林(1970- )，男，博士，副教授； 李貴祥(1990- )，男，在讀碩士

1009-6825(2015)22-0142-03

U418.66

A