某迫擊炮座鈑拓撲優化設計
張孝明,劉樹華,彭克俠,劉幸國
(1.中北大學,太原 030051; 2.安陽出入境檢驗檢疫局,河南 安陽 455000)
?
某迫擊炮座鈑拓撲優化設計
張孝明1,劉樹華1,彭克俠1,劉幸國2
(1.中北大學,太原030051; 2.安陽出入境檢驗檢疫局,河南 安陽455000)
摘要:新的戰場需求對迫擊炮輕量化設計提出了要求,根據迫擊炮座鈑的受力情況,基于Hypermesh-OptiStruct軟件平臺建立有限元模型,通過對迫擊炮座鈑的拓撲優化完成改進設計,并利用AWE有限元軟件對優化后模型進行剛強度分析,通過分析證明優化方案的合理性;拓撲優化后,座鈑質量減少15.6%;該方法對迫擊炮改進設計具有一定的參考價值。
關鍵詞:迫擊炮;座鈑;拓撲優化;剛強度分析
迫擊炮自問世以來一直是支援和伴隨步兵作戰的一種有效的壓制兵器,是步兵極為重要的常規兵器,具有結構簡單、機動性良好的特點。為使迫擊炮更加適應現代戰場,減少炮組成員的武器攜帶質量,提高作戰效率和機動性,我們以某型迫擊炮座鈑為研究對象,依據迫擊炮發射時的結構受力特性和技術設計要求,對迫擊炮座鈑進行拓撲優化設計。優化設計能夠提高迫擊炮座鈑的結構性能,滿足結構的輕量化設計要求,降低研發成本和減少研發周期,在生產過程中已經成為至關重要的一部分。
以某型號迫擊炮座鈑結構為優化對象,依據迫擊炮射擊時座鈑結構受力情況,在滿足剛強度要求的情況下,以減輕其質量為目標,運用拓撲優化方法尋求多射角工況下座鈑的最佳材料分布,對座鈑的結構進行輕量化設計。
1原座鈑剛強度分析
1.1材料的選擇
迫擊炮座鈑使用的材料為鋁合金材料,其材料密度為2.7×103kg/m3,彈性模量為70 MPa,泊松比為0.3,許用應力為450 MPa。
1.1迫擊炮座鈑的受力分析
如圖1所示忽略身管、炮尾的重力,迫擊炮座鈑在發射過程中主要承受以下作用力:Fpt為炮膛合力;Fgc為后坐部分(除座鈑)的慣性力;Fgb為座鈑的慣性力;FT1,FT2土壤的作用力。
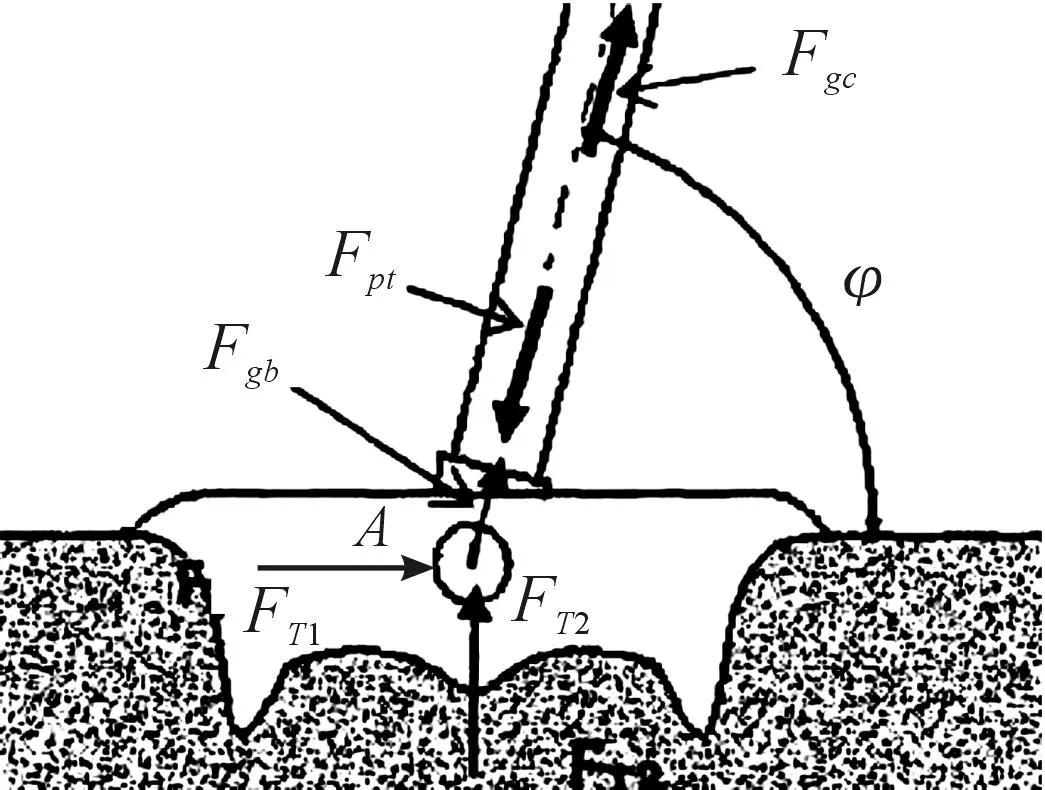
圖1 迫擊炮座鈑的受力特性
在靜力學分析中,通常考察最大后坐力靜載下座鈑的結構剛強度。假設迫擊炮后坐部分質心在身管軸線上,忽略座鈑的慣性力,則后坐力F=Fpt+Fgc。
1.2原座鈑模型的建立與靜力學仿真分析
原座鈑是V型筋鈑的圓形窗式座鈑,劃分網格與施加約束如圖2所示。
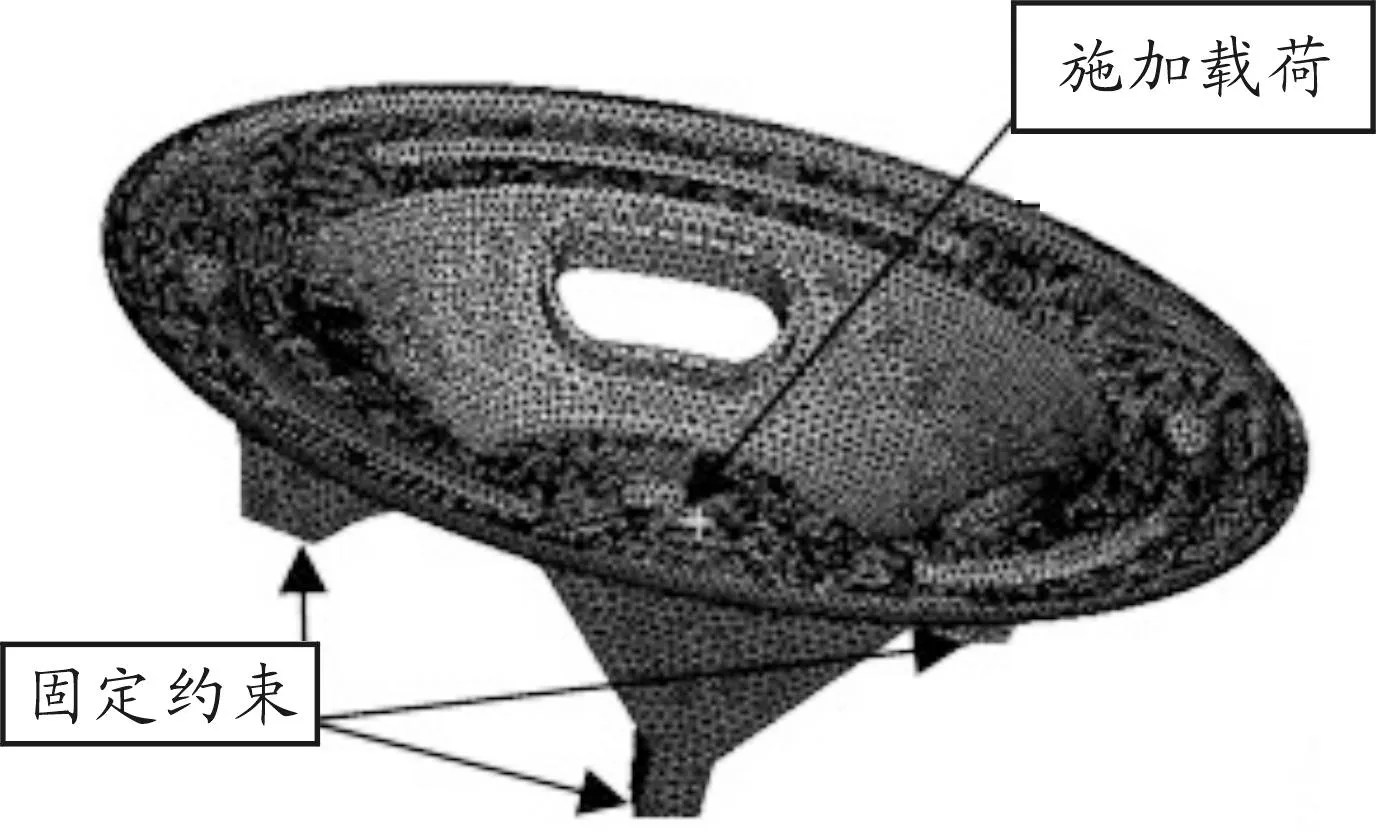
圖2 原迫擊炮座鈑有限元模型
將原迫擊炮座鈑模型導入AWE軟件中,在炮尾處施加膛底最大壓力34.95 MPa,邊界條件為在迫擊炮駐鋤底部施加固定約束。
迫擊炮在射擊時座鈑通常有兩種放置方式,一種是構筑工事,將座鈑置入構筑好的土壤工事中;另一種是將迫擊炮放置在硬質土壤上,如水泥地等,射擊時允許的射角為70°至85°,小于70°時座鈑有滑倒的可能。由于土壤通常對座鈑有緩沖作用,第1種情況下射擊時,迫擊炮座鈑的應力、應變均要小于第2種情況。因而在對迫擊炮座鈑輕量化設計中,研究最惡劣的情況,即在硬質地面水平放置射擊。因此,利用AWE軟件只分析計算迫擊炮座鈑在75°和85°兩種射角、0°和60°兩種方向角共4種工況下的剛強度,如表1所示。其中0°時,射角后支點為一個駐鋤;60°射角時,后支點為兩個駐鋤。
從迫擊炮座鈑的剛強度分析中可以看出:迫擊炮座鈑的最大應力和最大位移均出現在高低角75°、方向角0°的情況下,且最大位移為1.996 4 mm,最大應力為 424.51 MPa;4種工況下的原迫擊炮座鈑的最大應力均分布于迫擊炮座鈑底部駐鋤處,而在迫擊炮座鈑的上表面的應力分布均較小;從4種工況中可以看出,迫擊炮座鈑整體的剛度和強度有優化的富余量,可以進行拓撲優化。
表1原迫擊炮座鈑剛強度分析結果
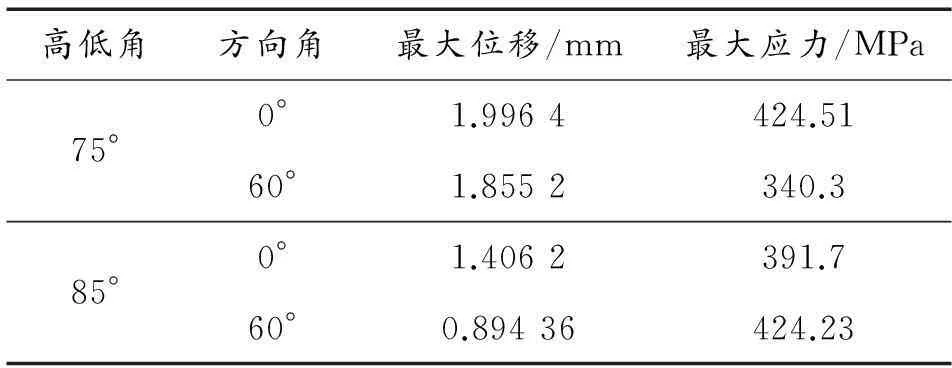
高低角方向角最大位移/mm最大應力/MPa75°0°1.9964424.5160°1.8552340.385°0°1.4062391.760°0.89436424.23
2座鈑的優化設計
2.1數學模型
OptiStruct軟件的拓撲優化技術包含了設計變量、約束條件以及目標函數3個要素, 引入朗格朗日乘子:
朗格朗日方程最小化條件:
其中f(X)是設計目標,如各種力學性能或者重量;g(X)是需要進行約束的響應,如對物體工作時的變形和應力水平進行約束[4]。
2.2拓撲優化模型
去除不重要的部分,通過三維畫圖軟件UG建立座鈑模型,并導入到Hypermesh軟件中,進行網格劃分,建立的有限元模型如圖3所示。
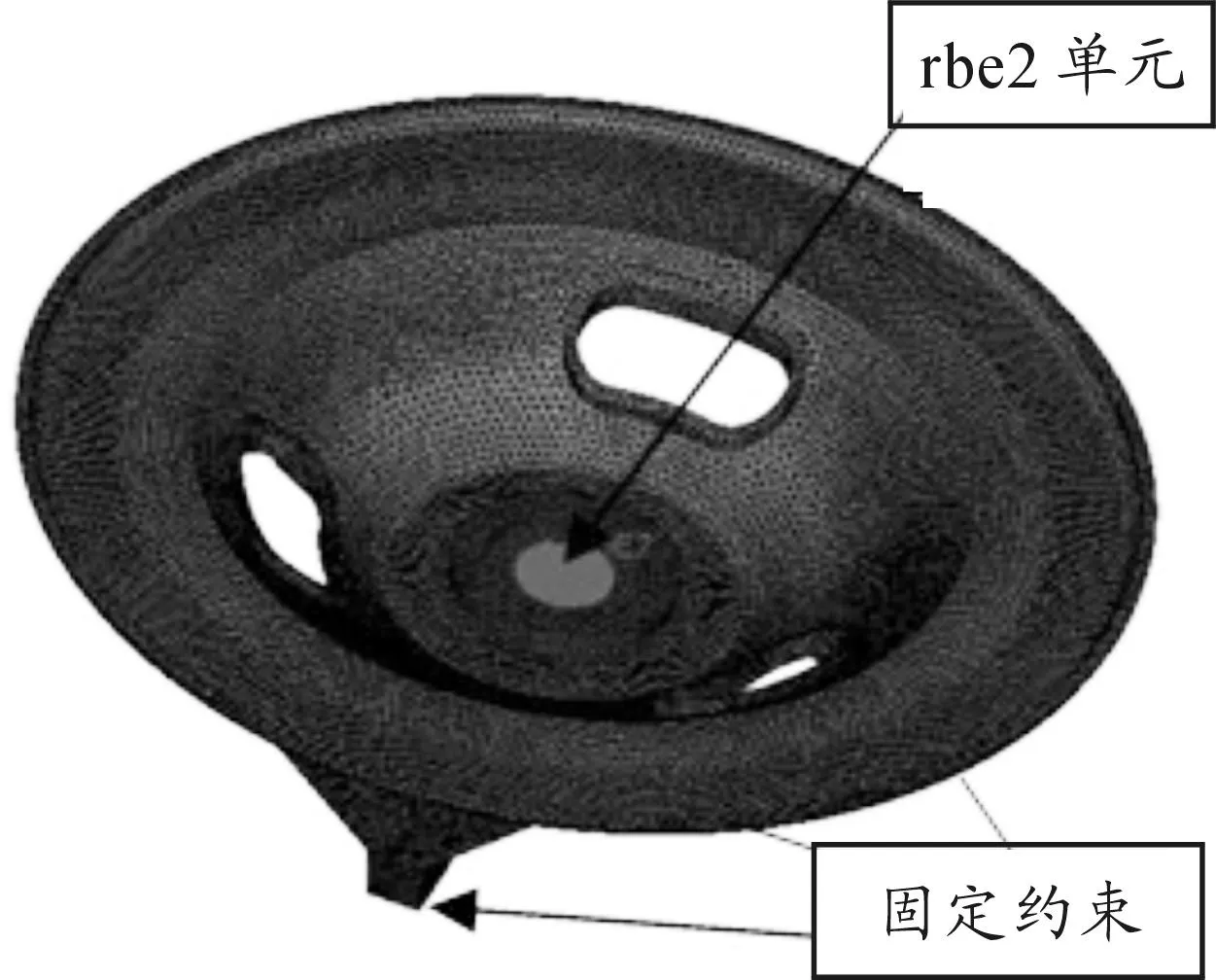
圖3 原迫擊炮座鈑的有限元模型
用Optistrict軟件進行拓撲優化為使得添加載荷方便,模型中炮尾處添加剛性單元rbe2來定義載荷作用位置[2-3]。在對迫擊炮座鈑的優化設計過程中,考慮到火力部分的安裝布置,為了避免優化結束后結構的改變使其安裝發生干涉現象,將與炮尾接觸相接觸處以及駐鋤與地面接觸處考慮為受載關鍵部位,其結構不能發生變化,故而將其設置為非設計區;將其他部分設置為設計區,對其進行拓撲優化設計。
1) 目標函數:以座鈑體積最小為目標函數;
2) 約束條件:在對迫擊炮進行拓撲優化時,將stress約束為靜力分析時的最大應力值;
3) 施加載荷:根據實驗測得迫擊炮發射時的炮膛合力變化規律,取膛底壓力最大值進行優化設計計算。考慮迫擊炮可以進行360°射擊,因而在施加載荷時,設置方向角0°、+60°、120°、180° 4種工況施加載荷,將模型的優化過程設置為對稱約束;
4) 設計變量:將單位相對密度作為迫擊炮座鈑的設計變量。
2.3拓撲優化結果
基于OptiStruct軟件21次優化迭代后,計算收斂,去除密度閥值小于0.01單元后的優化結果密度分布圖如圖4所示。
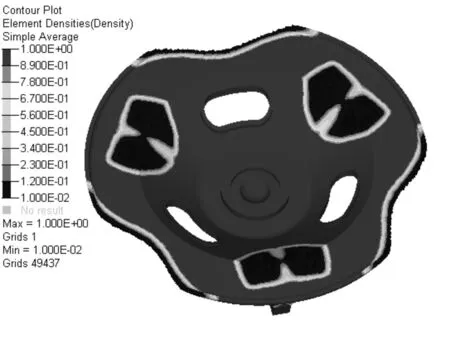
圖4 去除密度閥值小于0.01單元后結果
初次拓撲優化的結果顯示出迫擊炮座鈑的傳力路徑和加強筋板的布置,但是還需要在此基礎上進行進一步的結構設計,才能將其應用于實際工程中去。
在進一步結構設計過程中,經過分析設計,最終得到如圖5所示的設計方案。經過計算,優化后的迫擊炮座鈑質量降低了15.6%。
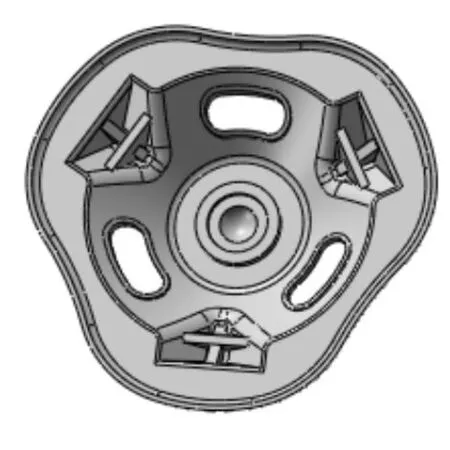
圖5 優化后的迫擊炮座鈑模型
3優化前后結構受力分析對比
優化后的迫擊炮座鈑去除了結構強度影響較小的區域,同時對迫擊炮加強筋的布局進行了設計。將優化后的迫擊炮座鈑建模并導入AWE軟件中進行剛強度分析,將分析結果與原座鈑進行對比,結果如表2所示。
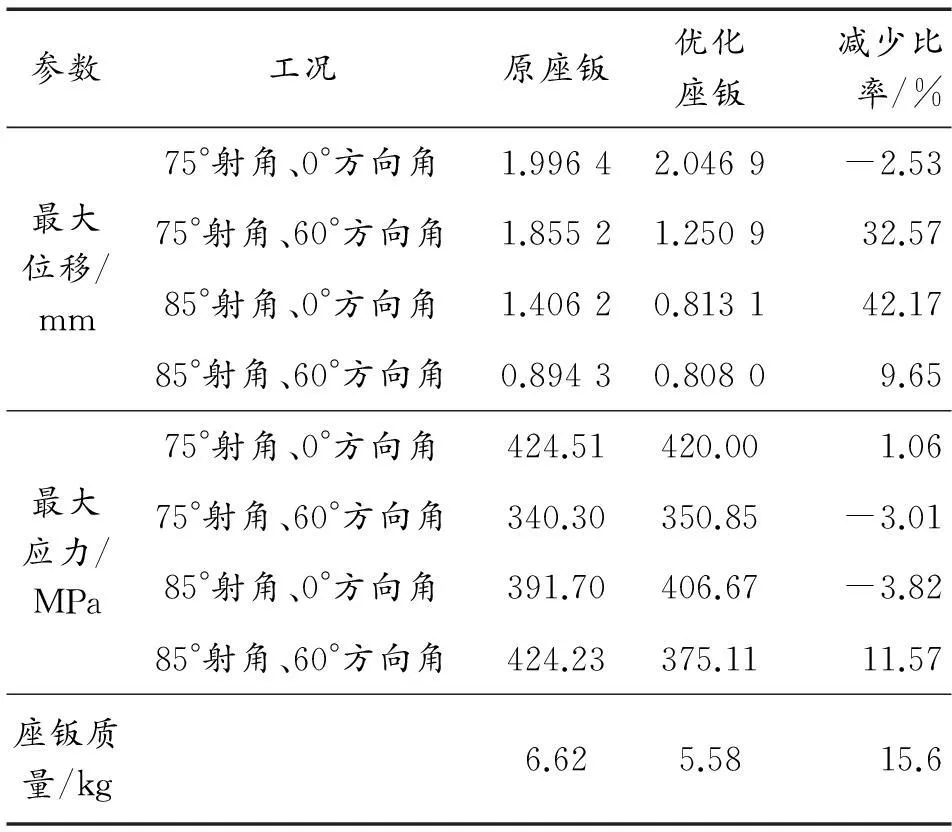
表2 迫擊炮座鈑優化前后對比
從表2中可以看出,優化后的最大等效應力比原迫擊炮座鈑略有減小,但依舊比較大。分析其原因,可能是去除材料主要是主鈑的部分,而駐鋤部分并沒有太大的變化,所以應力變化不大,材料的減少也會使某些部位所受應力增大。優化后迫擊炮座鈑的最大位移除在70°射角、0°方向角時有小幅增加,在其他工況下均有較大的改善,說明優化效果較好。表2中的計算結果顯示優化后的迫擊炮座鈑的剛強度符合其設計要求,該迫擊炮座鈑達到了優化的目的。
4結論
經過對某迫擊炮座鈑的結構優化設計與力學分析,其質量得以降低15.6%。優化后其最大應力符合設計要求。可以看出,通過Optistruct軟件中拓撲優化方法得到的結果模型是一種承載受力比較合理的結構。迫擊炮座鈑的輕量化設計對降低部隊士兵的攜重,提高作戰效率具有重要意義。
參考文獻:
[1]唐治.迫擊炮設計[M].北京:兵器工業出版社,1994.
[2]張海航.某火炮上架結構拓撲優化設計[J].彈道學報,2009(2):83-85,89.
[3]梁傳建.及多射角工況的火炮上架結構優化設計[J].火炮發射與控制學報,2014(2):30-34.
[4]洪清泉.OptiStruct & HyperStudy理論基礎與工程應用[M].北京:機械工業出版社,2013.
[5]李琳,薛錚.等強度三維空心葉片的內部拓撲結構[J].航空動力學報,2012,27(10):2329-2335.
[6]關英俊,辛宏偉,趙貴軍,等.空間相機主支撐結構拓撲優化設計[J].光學精密工程,2007(8):1158-1162.
[7]浦廣益.ANSYS Workbench 12基礎教程與實例詳解[M].北京:中國水利水電出版社,2010:243-245.
[8]潘玉田,馬新謀.履帶式自行火炮負重輪輪轂輕量化技術研究[J].火炮發射與控制學報,2009(2):41-44,49.
[9]范文杰,范子杰,蘇瑞意.汽車車架結構多目標拓撲優化方法研究[J].中國機械工程,2008,19(2):1505 -1507.
[10]羅震,郭文德,蒙永立,等.全柔性微型機構的拓撲優化設計技術研究[J].航空學報,2005,26(5):617-625.
(責任編輯周江川)
本文引用格式:張孝明,劉樹華,彭克俠,等.某迫擊炮座鈑拓撲優化設計[J].兵器裝備工程學報,2016(4):33-35.
Citation format:ZHANG Xiao-ming, LIU Shu-hua, PENG Ke-xia, et al.Topological Optimization Design for Mortar’s Base Plate[J].Journal of Ordnance Equipment Engineering,2016(4):33-35.
Topological Optimization Design for Mortar’s Base Plate
ZHANG Xiao-ming1, LIU Shu-hua1, PENG Ke-xia1, LIU Xing-guo2
(1.North University of China, Taiyuan 030051, China; 2.The Entry and Exit Inspection and Quarantine Bureau of Anyang, Anyang 455000, China)
Abstract:To satisfy the demand of the new battleground, lightweight design of mortar was put forward. According to the force of the mortar base plat, we established finite element model based on Hypermesh-OptiStruct software. Then, using topology design of mortar’s base plate, we completed the design of improvements. The stiffness and strength of the optimized model were analyzed with the AWE finite element software. It proved the rationality of optimization plan through the analysis. After topology optimization, the mass of mortar’s base plate is decreased by 15.6%. This topology design wil have some reference to the design of mortar’s base plate.
Key words:mortar; base plate; topology optimization; analysis of stiffness and strength
文章編號:1006-0707(2016)04-0033-04
中圖分類號:TJ31
文獻標識碼:A
doi:10.11809/scbgxb2016.04.009
作者簡介:張孝明(1990—),男,碩士研究生,主要從事火炮總體設計技術研究。
收稿日期:2015-09-23;修回日期:2015-11-03
【裝備理論與裝備技術】

