一種前沿推進的自適應三角網生成算法
馬 鈞 霆,陳 鎖 忠,劉 歡,張 潔
(南京師范大學虛擬地理環境教育部重點實驗室,江蘇 南京 210023)
?
一種前沿推進的自適應三角網生成算法
馬 鈞 霆,陳 鎖 忠*,劉 歡,張 潔
(南京師范大學虛擬地理環境教育部重點實驗室,江蘇 南京 210023)
現有前沿推進算法在利用前沿推進法對二維平面區域進行自適應三角網剖分時,由于前沿邊形態包含復雜的幾何特征,導致網格單元質量不高、算法速度慢、魯棒性低。該文提出一種兼顧三角單元質量及魯棒性的三角網生成算法。首先,將前沿邊內向推進過程中的所有形態歸納為4種類型;然后利用候選網格點試探算法構建最優三角單元,并通過相鄰前沿線段內夾角搜索閾值分級讓步的方式維護算法魯棒性。實驗表明:該算法能夠快速識別并處理復雜的前沿邊形態特征,生成單元疏密過渡均勻且質量較高的自適應三角網。
前沿推進法;自適應三角網;讓步算法;網格質量
在諸多網格生成算法中,前沿推進法[1,2]對邊界擬合性能優越,生成網格質量好、網格單元疏密過渡平滑,是較為主流的網格生成算法之一。長期以來,對其研究主要圍繞兩方面:一為AFT算法提供尺寸信息的背景網格的構建方法[3,4];二是復雜形態前沿邊影響下候選網格點最優位置計算方法及單元構建策略[5,6]。對于背景網格構建問題,現有許多研究指出,可通過模擬介質的幾何特征自動識別算法構建背景網格[7,8];也有學者提出可采用調和函數作為背景網格的基本信息[4];而對于候選網格點的位置計算方法,多在傳統前沿推進算法的基礎上,依據經驗對單元構建策略進行完善和改進,在背景網格尺寸變異較大區域,往往導致網格出現無法收斂的情況[9]。為此,本文充分考慮前沿邊復雜形態影響下網格單元質量的受損機制及最優單元構建策略,提出了一種兼顧三角單元質量及魯棒性的自適應網格生成算法,該算法能夠快速識別并處理復雜的前沿邊形態特征,生成單元疏密過渡均勻且質量較高的自適應三角網。
1 算法概述
基于現有前沿推進法的基本過程[10],提出如下改進的算法:1)邊界離散和前沿邊的初始化;2)選取一條前沿線段,從背景網格中提取期望單元尺寸,結合選中前沿線段長度計算最優網格單元尺寸[11];3)計算候選網格節點,依據其與前沿邊的拓撲關系及當前所選線段與相鄰線段之間夾角大小,自動識別當前的前沿邊形態類型;4)調用單元構建策略,形成有效網格單元,更新前沿邊及網格的拓撲關系;5)判斷前沿邊中所包含前沿線段數量是否為0,若為0即完成網格的生成,否則執行步驟2。
與傳統前沿推進法相比,本算法引入了前沿邊形態類型自動識別算法,所設計的最優單元構建策略模塊可被快速檢索與調用以生成自適應網格。
2 前沿邊形態類型與單元構建策略
2.1 基本形態與策略分析
隨著前沿線段的推進,新建單元邊與前沿邊出現交叉或距離太近的情況。此時,通過數次減小最優單元尺寸的方式[12],重新嘗試構建網格單元。若多次減小單元尺寸后依然無法形成有效的網格單元,考慮如下單元構建策略:1)判斷當前所選線段與相鄰前沿線段之間的內夾角大小;2)若為銳角,則連接內夾角的兩個非公共點構建新三角單元,若新單元內部不包含其他網格點,則為有效單元,單元構建完成;3)若為鈍角,如圖1,作該鈍角的角平分線,設為AD,長度為最優單元尺寸h0,將鈍角分為兩銳角,分別連接CD、BD,在判斷單元有效性的基礎上,形成新單元;4)若兩個內夾角均大于180°,此時需進一步分析前沿邊形態特征,尋找可行的單元構建方案。為此,提出單元試探構建算法。
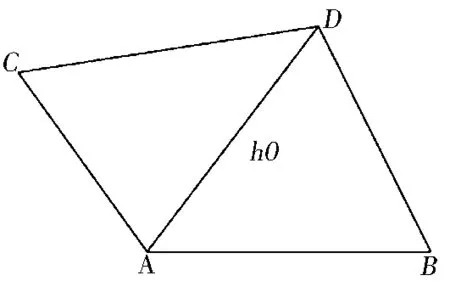
圖1 夾角為鈍角時的單元構建策略示意
Fig.1 Element construction strategy for obtuse angle situation
2.2 形態變更驅動的單元試探構建算法
針對傳統前沿推進算法可能引發前沿邊斷裂的問題[11],提出通過更改前沿邊形態的方式,驅動當前被選中前沿線段與其相鄰線段之間拓撲關系發生改變,并試探改變后的前沿邊形態是否支持構建有效單元。具體過程如圖2所示:線段AB為當前前沿線段,依據單元構建策略,無法形成有效單元;此時,以90°為閾值,遍歷前沿線段,搜尋到一個小于90°的夾角(∠ACE);連接AE,更新前沿邊,重復調用單元構建策略,此時前沿線段AB可與AE直接相連形成有效單元,完成單元構建。
上述算法可保證以當前線段為底邊形成有效單元。但若前沿邊包含的所有內夾角均大于給定閾值,依據上述算法,其形態將不發生變更,導致算法鎖死,故閾值不能設為定值。但不同的閾值對前沿邊形態的改變造成不同影響,因此需要設計閾值的動態調整策略。
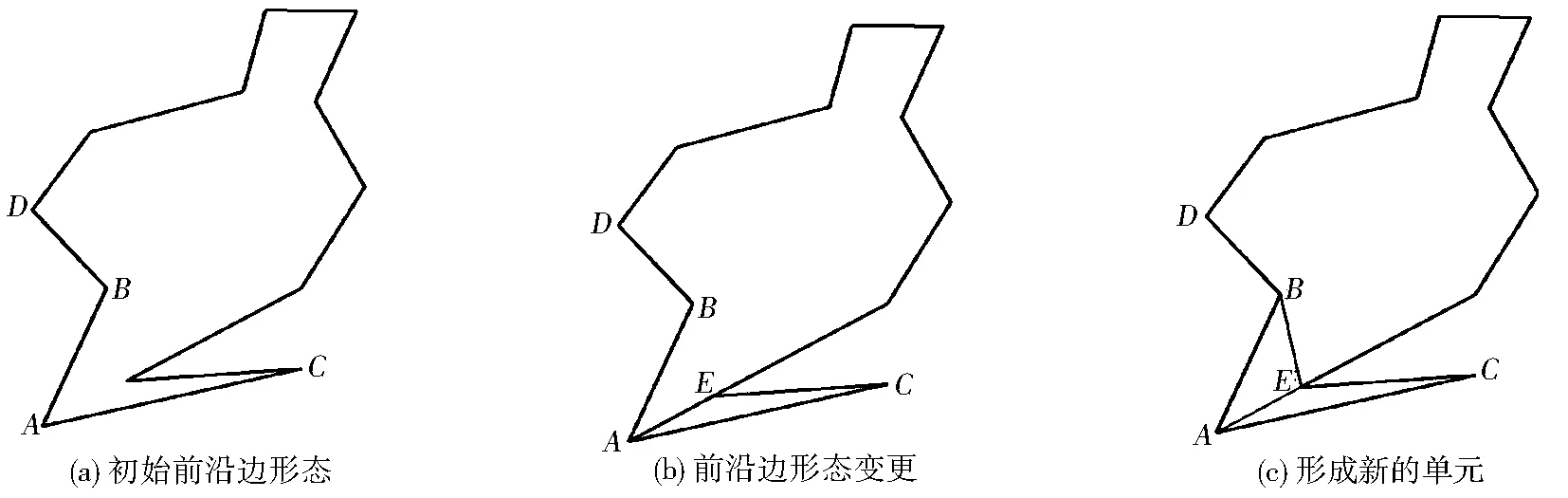
圖2 前沿邊形態變更驅動的單元構建方法
Fig.2 Element construction method driven by the front-line morphology changes
2.3 網格的發散與閾值分級讓步機制
前沿邊形態的改變與內夾角的搜索閾值有著密切關系。一般情況下,當搜索閾值為銳角時,新得前沿線段的長度與兩個作為夾角邊的前沿線段的平均長度相差不大,從而保證了新形成的單元尺寸的穩定性與收斂性。而當搜索閾值為鈍角時,則容易導致網格的發散效應,圖3所示為搜索閾值為較大的鈍角時出現的網格“發散”效應。
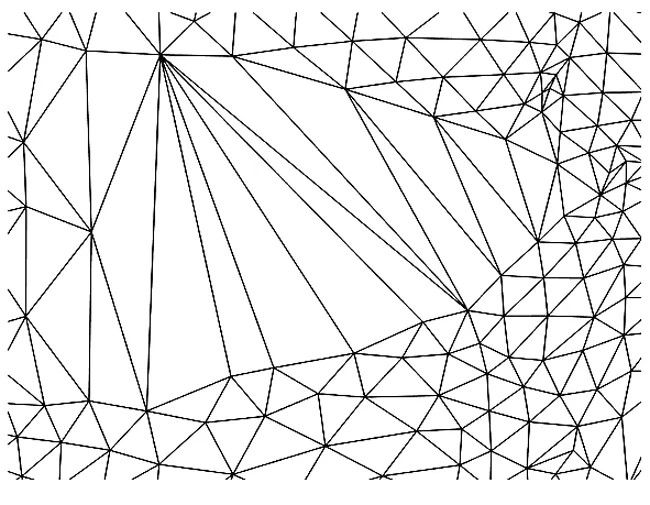
圖3 鈍角三角單元的“發散”效應
Fig.3 Obtuse triangle element “divergence” effect
為抑制這種“發散”效應,提出閾值的分級讓步機制:設定初始閾值為銳角,遍歷前沿邊包含內夾角;一次遍歷完成后,前沿邊形態如未發生任何變動,則將搜索角度閾值增加一個微小量,重復搜索過程,直到前沿邊形態發生有效變更。
2.4 前沿邊形態類型劃分
前沿邊形態變化較為復雜,但前沿邊與候選網格點之間的拓撲關系變化則有明顯規律,為規范算法框架,對其形態進行分類。分類思路為:針對一種前沿邊形態,首先依據傳統AFT算法構建新單元,若可形成有效單元,則視作理想的前沿邊類型;若無法形成有效單元,則依次嘗試不同備選策略構建新單元,將前沿邊形態劃分為4種類型(圖4):類型一:候選網格點滿足有效性要求;類型二:候選網格點未通過有效性檢驗,但當前所選線段與相鄰前沿邊線段之間內夾角為銳角,且連接該角度非公共點可形成有效三角單元;類型三:當前所選線段與其相鄰前沿邊之間內夾角為鈍角,通過做該鈍角的角平分線構建的單元為有效3角單元;類型四:前3種情況下均無法得到有效單元,此時采用單元試探構建算法和閾值分級讓步算法完成有效單元的構建。
以上4種類型涵蓋了所有可能出現的形態類型。所用備選策略的適用性依次增加,而構建格網單元質量依次降低。前沿推進過程中,大多數前沿邊形態屬于類型一和類型二,僅在背景網格中尺寸變異性較大或前沿邊交匯處,常見類型三或類型四的前沿邊形態。因此網格整體質量損耗得到了有效控制。

圖4 前沿邊形態分類示意
Fig.4 Front line geometric feature type diagram
3 自適應網格生成算法流程
前沿邊更新一般包括原有沿邊線段的刪除、插入及拓撲關系的重構三部分。可采用四叉樹[13]或Alternative Digital Tree(ADT)[14]的數據結構進行存儲,以提高更新效率。理論上講,前沿邊上任何一個前沿線段均可作為當前前沿線段被選取出來以構建網格單元,但一些文獻[15,16]已證明:每次選取長度最小的前沿線段時,所得網格過渡性更好。因此,本文選取長度最短邊作為當前前沿線段,網格生成算法具體步驟如下:
步驟1:單元尺寸背景網格構建,區域邊界離散、前沿邊的初始化。
步驟2:選中當前前沿邊上的最短線段,計算其中點位置處的最優網格單元尺寸和候選網格點位置。最優單元尺寸的計算公式[5]為:
(1)
(2)
式中:S為三角形單元面積,a、b、c表示三角單元三邊長度,s為三角形單元的實際尺寸,ρ為三角形單元在中點位置處從背景網格中提取的尺寸,α反映了三角形的形態質量[17],α取值范圍為(0,1),其值越接近1,三角形形態越接近正三角形,質量越好(表1)。
表1 三角單元形態及其α值示例
Table 1 Triangles quality and their α-quality

單元形態單元形態質量α1.00.980.720.45
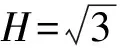
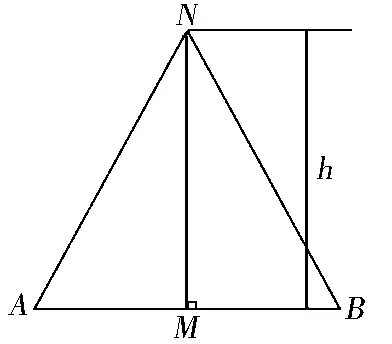
圖5 候選節點N的最優單元尺寸h示意
Fig.5OptimaloffsetheighthofcandidatepointN
求取待構建單元的最佳尺寸,令f=h/d,k=H/d,此時由式(2)可得:
(3)
F(f)=f3+2.25f-3k=0
(4)
取f0= 0,F(f0)=-3k,根據牛頓迭代法有:
(5)
(6)
由式(5)和式(6)經過數次迭代后,解得f的近似值,即得單元實際尺寸h0=f×d。依據h0所構建的單元能夠在單元的自適應性和形態質量之間取得最優平衡,h0即為構建網格單元的最優尺寸。
步驟3:若候選網格點所構建單元為無效單元,令h0 = 0.8×h0,重新計算候選網格點位置,并在h0 > |AB|/2的前提下,判斷能否形成有效單元。如能形成有效單元,則執行步驟8,否則執行步驟4。
步驟4:如當前選中線段與相鄰線段之間內夾角為銳角,且通過連接夾角非公共點可形成有效單元,則執行步驟8,否則執行步驟5。
步驟5:如當前選中線段與相鄰線段之間內夾角為鈍角,且通過作該夾角角平分線可形成有效單元,則執行步驟8,否則執行步驟6。
步驟6:設定閾值,遍歷前沿邊包含內夾角,搜尋角度小于閾值的內夾角,若嘗試連接該夾角的非公共點能形成有效單元,且改變后的前沿邊形態支持連接當前選中線段與其相鄰線段非公共點而形成有效單元,則執行步驟8,否則執行步驟7。
步驟7:給閾值增加一微小量,通常為5°或10°,執行步驟6。
步驟8:構建新的網格單元,更新前沿邊和網格的拓撲關系,判斷前沿邊中包含前沿線段個數,如大于0則執行步驟2,如等于0則完成網格的生成,退出算法。
4 網格的優化與平滑
提出鄰域多邊形最優原則。如圖6,ΔABC為形態質量較低、待刪除的三角形單元,其最短邊BC周圍所有相鄰的三角形共同組成了多邊形AP1P2……P5,如多邊形內角均小于180°且銳角數目不大于3,即是凸多邊形,此時約定ΔABC滿足鄰域多邊形最優原則。鄰域最優基礎上,刪除與待優化單元相鄰的三角單元,計算該單元最短邊中點,將其與多邊形各頂點相連,構建新的三角單元,完成單元的優化。如果該鄰域多邊形非凸,還應對其凸化(圖7):搜索第一個大于180°的角,提取其兩相鄰邊記為Li、Lj;連接Li、Lj的非公共節點,形成新邊Ln;用Ln取代Li和Lj,更新鄰域多邊形邊拓撲關系;循環以上過程直至鄰域多邊形為凸。
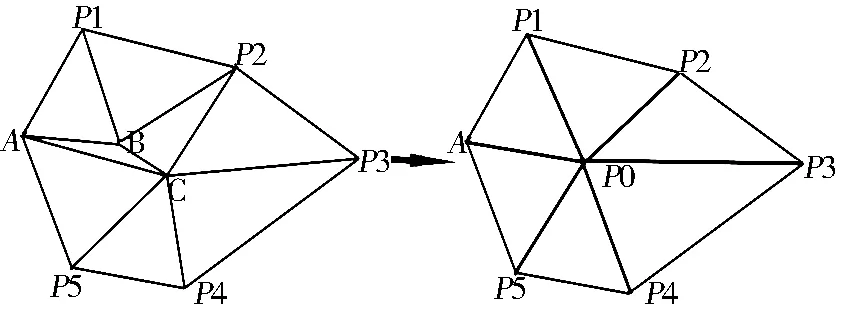
圖6 狹長三角形單元的優化過程示意
Fig.6Longnarrowtriangleelementoptimizationdiagram
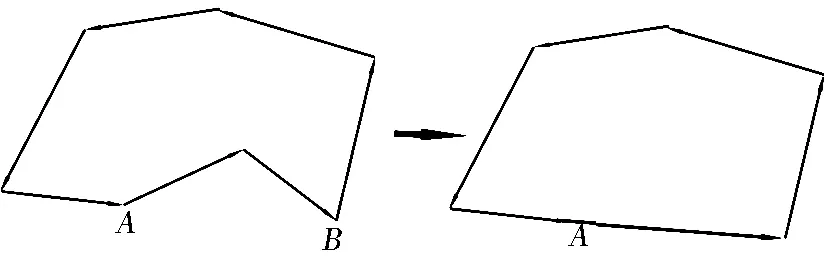
圖7 鄰域多邊形優化算法示意
Fig.7Adjacentpolygonoptimizationalgorithmdiagram
5 算法分析與實例
5.1 算法效率分析
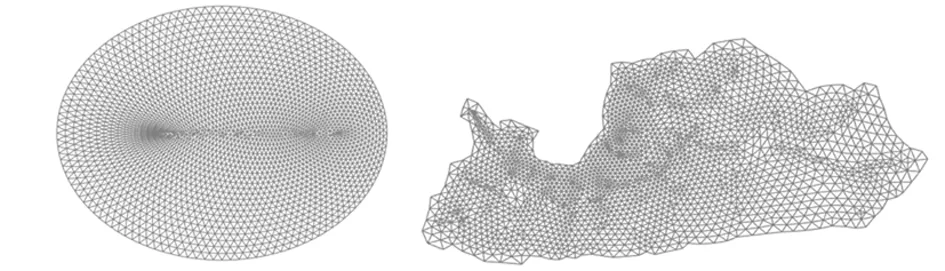
設網格邊界包含初始前沿邊線段Nb個,算法執行過程中,在每嘗試構建一個新單元時,都包含線段的交叉檢驗或遍歷整個前沿邊的搜索操作,該步驟算法時間復雜度為O(Nb);在計算單元尺寸ρ時,需要判斷M點處于背景網格的哪一個網格單元中,設背景網格包含NEb個單元,該步驟算法時間復雜度為O(NEb);設最終生成網格包含Ne個單元,由于每個單元均需要從背景網格中提取尺寸信息,因此有:O(Ne)=O(NEb)>O(Nb),可得整個網格構建算法時間復雜度為O(Ne2)。引入ADT數據結構[14]存儲背景網格信息,背景網格尺寸提取的搜索算法時間復雜度變為O(log2(NEb)),由于O(log2(NEb)) 5.2 算例 基于OpenGL可視化引擎,使用VC語言開發有限元自適應網格生成系統,對本文算法進行檢驗。網格整體質量作為衡量生成網格優劣的標準,其計算公式為: (7) 式中:Q表示網格整體質量;Ne表示該網格中包含單元個數;αi表示第i個三角單元的形態質量,其計算方法見式(1)。 圖8、圖9為采用本文算法生成的自適應三角網,其單元尺寸由左圖中的背景網格提供。左圖中明暗程度代表該位置處網格單元期望尺寸,右圖為對應的自適應三角網。結果表明:生成的網格與背景網格擬合度較高、網格單元過渡性平滑、單元整體質量較高,背景網格能靈活控制網格的自適應方式。 圖8 橢圓形區域的背景網格及自適應離散結果(算例1) Fig.8Backgroundsizegridandgeneratedadaptivemeshofanovalarea 圖9 不規則多邊形區域的背景網格及自適應離散結果(算例2) Fig.9Backgroundsizegridandgeneratedadaptivemeshofanarbitrarypolygonarea 5.3 算例效率分析 表2顯示上述算例在執行網格生成、優化與平滑步驟時所需的時間數據。由表2可見:算法執行優化操作時,需要進行多次全局判斷,耗時超過15s,效率低下。優化后網格單元整體質量提升程度有限,這是由于算法所得到的網格本身具備較高的網格質量;相對而言,網格的生成與平滑過程耗時不超過1s,算法效率較高,且所構建網格優化前的平均質量接近0.9。 表2 自適應網格單元生成耗時數據 Table2Adaptivemeshgenerationtimeconsumingdata 實例單元數總體耗時(s)生成耗時(s)優化耗時(s)平滑耗時(s)優化前網格質量優化后網格質量算例1467615.8320.46715.0230.340.8990.914算例2459138.3780.61237.4860.280.8920.913 5.4 網格質量分析 圖10為基于同樣的背景網格,使用傳統的前沿推進法[18,19]得到的網格結果,表3給出了本算法和傳統算法所構建網格的質量數據。結果表明:本文算法形態質量在0.4以下的單元個數所占百分比小于5%(少數質量小于0.4的單元,一般是由前沿邊推進過程中發生交匯導致);對于邊界形狀較規則、尺寸變異平緩區域,前沿邊推進過程中交匯次數少,該類型單元數目相應減少。較之于傳統的前沿推進法,本文所提算法耗時較短,生成的自適應網格質量較優,具有良好的過渡性與自適應性。 圖10 使用傳統前沿推進算法得到的自適應網格 Fig.10 Adaptive triangular mesh generated by traditional AFT algorithm 表3 自適應網格質量數據 Table 3 Adaptive mesh quality data 實例方法T(s)NeQQtQbP(Qe<0.4)P(0.4 注:T表示計算時間,Ne表示網格含單元數量,Q表示網格整體質量,Qt表示最優形態單元質量,Qb表示最差形態單元質量,P表示單元質量滿足某數值的單元所占百分比,Qe表示單個單元形態質量。 本文充分研究了前沿邊推進的形態變化特征,對前沿邊形態進行分類并設計相應的網格單元構建策略;在前沿邊形態特征復雜區域,采用閾值分級讓步算法維護網格的單元質量與收斂性;通過前沿邊形態變更驅動的單元構建試探法避免冗余操作,維護網格生成算法在尺寸變異復雜區域的通用性;對于前沿交匯處網格質量下降問題,提出鄰域多邊形最優原則的網格優化算法對單元質量進行彌補。將以上方法融入傳統前沿推進算法,提出一種可以兼顧算法魯棒性和網格單元質量的網格生成算法。實驗結果表明該算法效率較高,生成網格疏密過渡平滑且質量較優,能夠根據背景網格的尺寸做出自適應調整、滿足實際的應用要求。 本算法雖對傳統的前沿推進法做出了一些改進,但對于前沿邊交匯處單元質量不高的問題未能給出完善的解決方案。如何進一步提升網格優化的效率,降低前沿邊“交匯”效應,是后續研究有待解決的一個關鍵問題。 [1] LO S H.A New mesh generation scheme for arbitrary planar domains[J].International Journal for Numerical Methods in Engineering,1985,21:1403-1426. [2] CAVENDISH J C.Automatic triangulation of arbitrary planar domains for the finite element method[J].International Journal for Numerical Methods in Engineering,1974,11:1041-1043. [3] 葉正寅,楊永年.非結構網格生成技術中一種直接提供背景信息的方法[J].西北工業大學學報,1999,17(1):1-5. [4] 武潔,馮晉利.三角形網格生成方法中一種提供背景信息的方法[J].計算機輔助設計與圖形學報,1999,11(4):300-303 [5] FRYKESTIG J.Advancing front mesh generation techniques with application to the finite element method[D].Chalmers University of Technology,Gothenburg Sweden,1994. [6] 孫力勝,鄭建靖,陳建軍,等.二維自適應前沿推進網格生成[J].計算機工程與應用,2011,47(3):146-148. [7] 黃曉東,杜群貴,葉邦彥,等.二維幾何特征自適應有限元網格生成[J].計算機輔助設計與圖形學報,2004,16(7):923-927. [8] 梁義,陳建軍,陳立崗,等.幾何自適應參數曲面網格生成[J].計算機輔助設計與圖形學報,2010,22(2):327-334. [9] 劉懷輝,楊興強.平面區域有限元三角網格剖分算法研究[D].濟南:山東大學,2007.37-39. [10] 修榮榮,徐明海.一種改進的二維平面區域三角形化的前沿推進法[J].石油大學學報(自然科學版),2003,27(5):73-80. [11] LEE C K, HOBBS R E.Automatic adaptive finite element mesh generation over arbitrary two dimensional domain using advancing front technique[J].Computer and Structures,1999,71:19-34. [12] FREY W H.Selective refinement:A new strategy for automatic node placement in graded triangular meshes[J].International Journal for Numerical Methods in Engineering,1987,24:2183-2200. [13] FAN N M,ZHANG Z F.An algorithm for large-scale terrain generation based on quad-tree[J].Advanced Research in Material Science and Mechanical Engineering,2014(446):946-990. [14] BONET J,PERAIRE J.An alternating digital tree(ADT) algorithm for 3D geometric searching and inter-section problems[J].International Journal for Numerical Methods in Engineering,1991,31(1):1-17. [15] SONG S H,WAN M.Robust and quality boundary constrained tetrahedral mesh generation[J].Communications in Computational Physics,2009,14(5):1304-1321. [16] GEOGRE P L,HEEHT F E.Automatic mesh generation with specified boundary[J].Computer Methods in Applied Mechanics and Engineering,1991,92:269-288. [17] DIMITRAKOPOULOS M,GRAF R.An efficient method for discretizing 3D fractured media for subsurface flow and transport simulations[J].International Journal for Numerical Methods in Fluids,2011,67:651-670. [18] 劉春太,楊曉東,陳靜波,等.任意平面區域的變尺寸有限元網格劃分[J].計算力學學報,2000,17(1):105-108. [19] 宋超,關振群,顧元憲.二維自適應網格生成的改進AFT 與背景網格法[J].計算力學學報,2005,22(6):694-698. Front Advancing Adaptive Triangular Mesh Generation Algorithm MA Jun-ting,CHEN Suo-zhong,LIU Huan,ZHANG Jie (KeyLaboratoryofVirtualGeographicEnvironment,MinistryofEducation,NanjingNormalUniversity,Nanjing210023,China) The front line morphology contains relatively complex geometrical characteristics as the front advancing inside the domain to be triangulated when using advancing front technique.Current AFT algorithms lead to a low quality generated mesh.In this paper,a mesh generation algorithm concerning both element quality and algorithm robustness is proposed.Firstly, all the possibly occurred front line geometric features are taken into consideration and summarized into four types.And then,in order to construct the triangular mesh element with best quality,a candidate point test algorithm is proposed and realized,and the algorithm′s robustness is maintained by using a compromise method that gradually increases the value threshold of searching angle between two adjacent front segments.The experiments demonstrate that the proposed mesh generator is capable of identifying and dealing with complex front line morphology,and discretizing the planar domain into a well-graded,high quality adaptive mesh with element size compatible with the user specification. advancing front technique;adaptive triangular mesh;compromise algorithm;mesh quality 2015-03-31; 2015-05-14 江蘇省高校自然科學研究重大項目(10KJA170028) 馬鈞霆(1987-),男,博士研究生,研究方向為地下水數值模擬與可視化方法。*通訊作者E-mail:junted_m@163.com 10.3969/j.issn.1672-0504.2015.05.004 P208 A 1672-0504(2015)05-0014-06
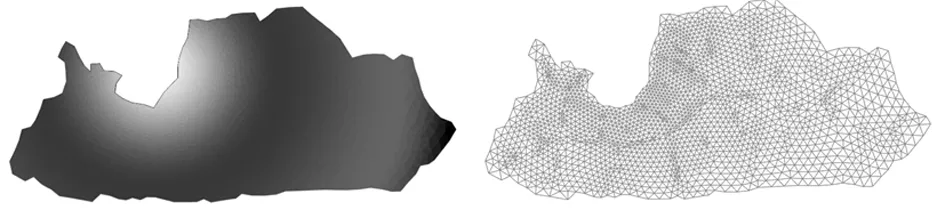


6 結語

