地震波數(shù)值模擬的褶積微分算子法與偽譜法的對比分析①

劉紅艷， 陳宇坤， 劉 芳

(天津市地震局，天津 300201)

地震波數(shù)值模擬的褶積微分算子法與偽譜法的對比分析①

劉紅艷， 陳宇坤， 劉 芳

(天津市地震局，天津 300201)

將基于Forsyte廣義正交多項(xiàng)式的褶積微分算子法運(yùn)用于復(fù)雜非均勻介質(zhì)地震波場模擬中，并將計(jì)算結(jié)果與偽譜法計(jì)算結(jié)果進(jìn)行分析比較。通過二者的計(jì)算時間對比發(fā)現(xiàn)：在同樣的計(jì)算條件下，褶積微分算子法的采樣時間始終小于偽譜法，這是其進(jìn)行地震波數(shù)值模擬的一個明顯優(yōu)勢。通過波場快照的對比，褶積微分算子法的模擬結(jié)果與偽譜法數(shù)值模擬結(jié)果的頻散效應(yīng)相當(dāng)，可為地震波場的值計(jì)算提供一種新的選擇。

褶積微分算子； 偽譜法； 地震波傳播； 數(shù)值模擬

0 引言

地震波場的數(shù)值算法和正演模擬歷來都是地震學(xué)研究的熱門領(lǐng)域。迄今為止，地震波場正演模擬的數(shù)值算法已有很多，如射線追蹤法[1-3]，積分方程法[1-6]，或基于波動方程直接解法的有限差分法[7-12]、偽譜法[12-17]、有限元法[18-19]和譜元法[20-22]，但大家很容易忽略如細(xì)胞自動機(jī)法[23]、辛幾何算法[24]、褶積微分算子法[25-31]、辛格式奇異核褶積微分算子[32-34]和Shannon奇異核褶積微分算子[35],這些也非常重要的數(shù)值計(jì)算方法。實(shí)際上它們都是吸收計(jì)算數(shù)學(xué)的一些思想，并成功地將其應(yīng)用于地震波場的數(shù)值模擬。

現(xiàn)有的各種地震波場正演數(shù)值模擬方法都存在自身的優(yōu)越性與局限性。本文的主要目標(biāo)就是研究一種已推出的、快速的、高精度的地震波場模擬方法(基于Forsyte廣義正交多項(xiàng)式的迭積微分算子法)，并將該算子所構(gòu)造的正演模擬算法運(yùn)用于復(fù)雜非均勻介質(zhì)模型的地震波場模擬中，同時將計(jì)算結(jié)果與偽譜法的計(jì)算結(jié)果做比較，以分析該方法的優(yōu)越性。

1 基本方程

二維均勻介質(zhì)中，一階速度-應(yīng)力彈性波動方程為

(1)

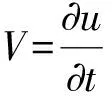
(2)

在二維各向異性介質(zhì)中，一階速度-應(yīng)力彈性波動方程是：

(3)

2 Forsyte廣義正交多項(xiàng)式褶積微分算子求導(dǎo)的基本原理

Forsyte 多項(xiàng)式是一個廣義正交多項(xiàng)式，其插值函數(shù)可寫為[29]：

(4)

其中，

p0=1

f(xi)為被插值函數(shù)f(x)在點(diǎn)xi處的值。式(4)中的p0(x)，…，pj+1(x)定義為Forsyte多項(xiàng)式系統(tǒng)。

對式(4)中的x求導(dǎo)，可得：

(5)

其中

Forsyte 多項(xiàng)式微分算子可寫為

(6)

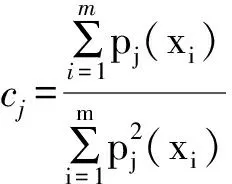
將式(6)離散化可得

(7)

式中，i為采樣指標(biāo)；Δx為沿著x軸的采樣間隔。在實(shí)際應(yīng)用中須將微分算子截成短算子，勢必引起Gibbs現(xiàn)象。另外，多項(xiàng)式的引入還將引起Runge現(xiàn)象。為了消除這些現(xiàn)象，必須采用窗函數(shù)以截?cái)嚅L微分算子。本文采用的Gaussian窗函數(shù)為

(8)

其中，mx為單邊截?cái)嚅L度的采樣數(shù)；c為常數(shù)；a(0.1≤a≤0.75)為衰減因子。將式(5)用式(6)截?cái)嗖忼X化后，可得實(shí)用的一階迭積微分算子：

(9)

通過對算子長度的調(diào)節(jié)及系數(shù)的優(yōu)化，可同時兼顧波場解的全局信息與局部信息。本文運(yùn)用算子長度為9 點(diǎn)的一階褶積微分算子求解彈性波場的一階速度-應(yīng)力方程。9 點(diǎn)迭積算子的最優(yōu)權(quán)系數(shù)為：-0.002 34，0.008 74，-0.027 4，0.085，0.0，-0.085，0.027 4，-0.008 74及0.002 34。可以看出算子的系數(shù)是反對稱的。圖1是9點(diǎn)微分算子振幅隨采樣點(diǎn)的變化曲線,從圖中可以看出算子振幅隨采樣點(diǎn)很快地衰減。

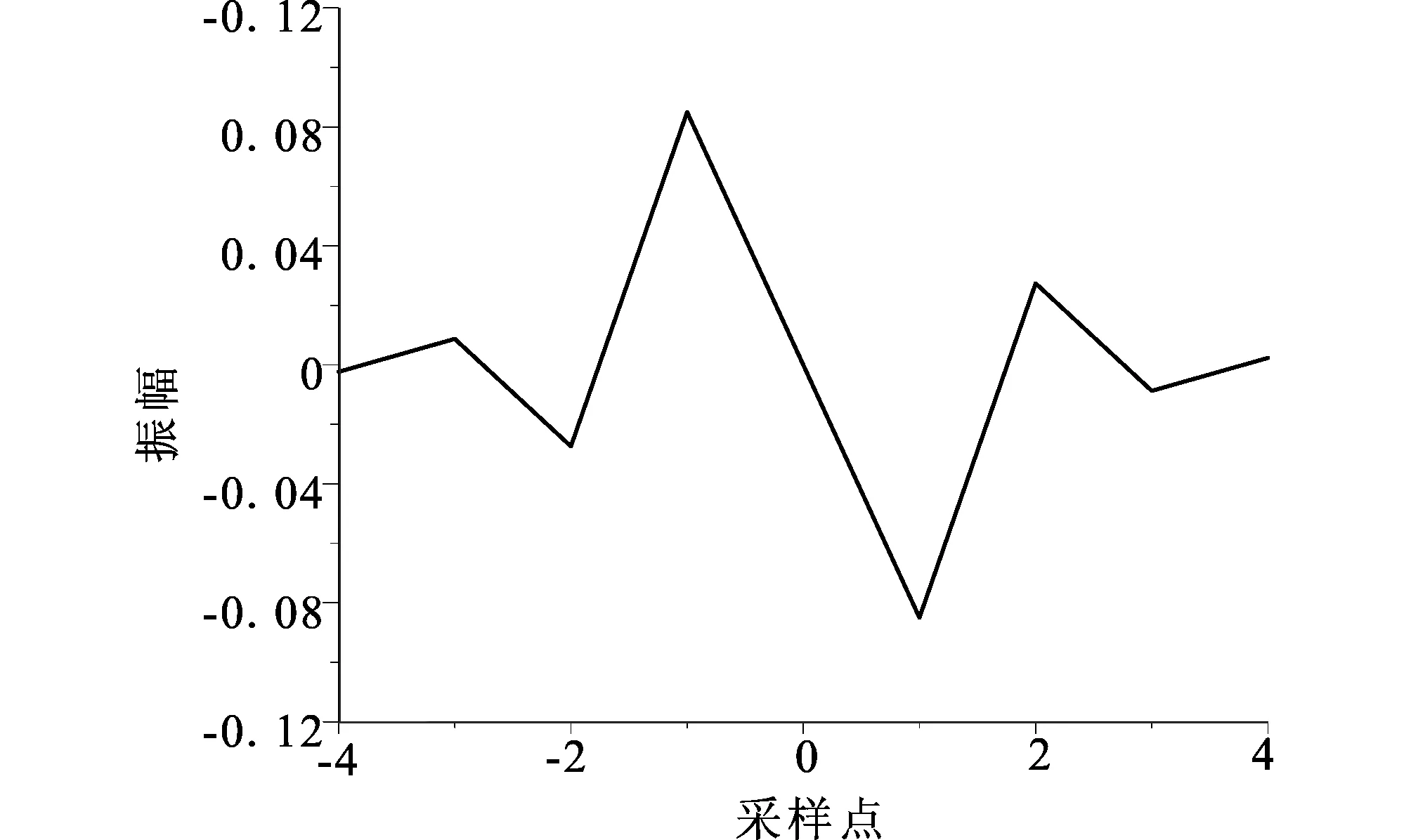
圖1 9點(diǎn)褶積微分算子振幅隨采樣點(diǎn)的變化曲線Fig.1 Amplitude versus sampling point for nine-point convolutional differentiator

3 偽譜法求導(dǎo)的基本原理

偽譜法是地震波場數(shù)值模擬諸多方法中使用較多的一種方法，其基本原理就是在空間域中通過FFT將空間域變換到頻率-波數(shù)域中，然后再通過傅里葉求導(dǎo)方式來進(jìn)行求導(dǎo)，從而避免了空間域中的直接求導(dǎo)。

對于二維波動方程，水平分量u的傅里葉變換為

(10)

由傅里葉變換的微分性質(zhì)

(11)

對式(11)進(jìn)行反傅里葉變換得

(12)

傳統(tǒng)偽譜法在求解時間導(dǎo)數(shù)的時候采用二階中心差分的形式，其求解方式為：

(13)

(14)

其中，Δt是時間采樣率。

4 數(shù)值模擬實(shí)例及分析

利用三個不同特性和幾何結(jié)構(gòu)的模型對褶積微分算子法和經(jīng)典偽譜法作比較，檢驗(yàn)兩種方法在刻畫波場精細(xì)細(xì)節(jié)和抑制頻散方面的效果。

4.1 大角度傾斜界面模型

圖2所示為大角度傾斜界面模型。網(wǎng)格大小為256×256，網(wǎng)格空間步長為10 m，時間步長為1 ms，震源位于格點(diǎn) (140,130) 處，介質(zhì)其他參數(shù)見表1。

表1 大角度傾斜界面模型參數(shù)

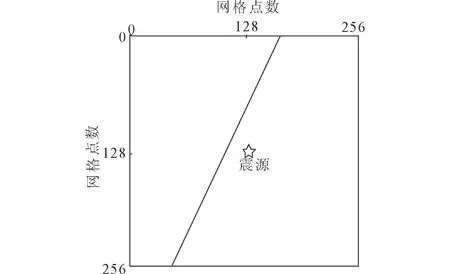
圖2 大角度傾斜界面模型示意圖Fig.2 Diagram of large-angle dipping interface model

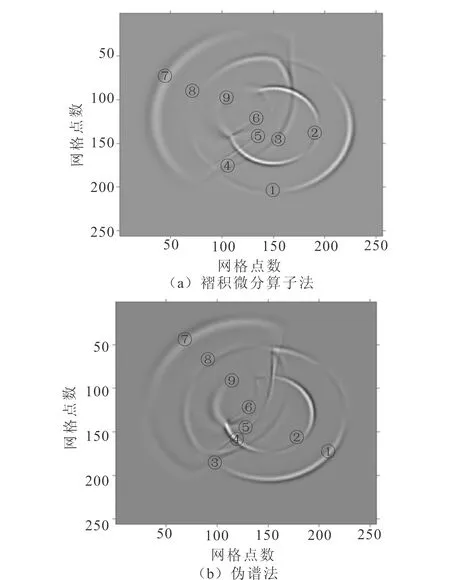
①直達(dá)波P1；②直達(dá)波S1；③同類反射波P1P1；④轉(zhuǎn)換反射波P1S1；⑤轉(zhuǎn)換反射波S1P1；⑥同類反射波S1S1； ⑦同類透射波P1P2；⑧轉(zhuǎn)換透射波P1S2；⑨同類透射波S1S2

圖3為波場快照。可以看到：兩層介質(zhì)波速差異很大，使其波阻抗差別也很大，導(dǎo)致兩層界面之間出現(xiàn)了很強(qiáng)且十分明顯的反射和透射。同樣，在介質(zhì)中由于波傳播時發(fā)生分裂(即分裂為橫波和縱波)，且縱波波速較橫波大，可以判斷外層圓為縱波快照，內(nèi)層圓為橫波快照。橫波和縱波在與波傳播方向垂直與平行方向上的差異同單一均勻介質(zhì)相似。但當(dāng)波通過界面時，在其左側(cè)可以看到四個圈層，由左向右分別是透射P波和轉(zhuǎn)換S波，以及轉(zhuǎn)換P波和透射S波；在右側(cè)亦對應(yīng)地出現(xiàn)反射P波和S波以及轉(zhuǎn)換P波和透射S波。由它們的反射點(diǎn)，可以很清晰地辨別兩層幾面所在。比較二者的波場快照可以發(fā)現(xiàn)，二者的頻散效應(yīng)基本相當(dāng)。但是從圖4所示的時間曲線上可以發(fā)現(xiàn)，在計(jì)算相同空間步數(shù)的時候，褶積微分算子法的用時要明顯少于偽譜法，這是由于偽譜法是一種全局算法，而褶積微分算子法是一種局部算法。

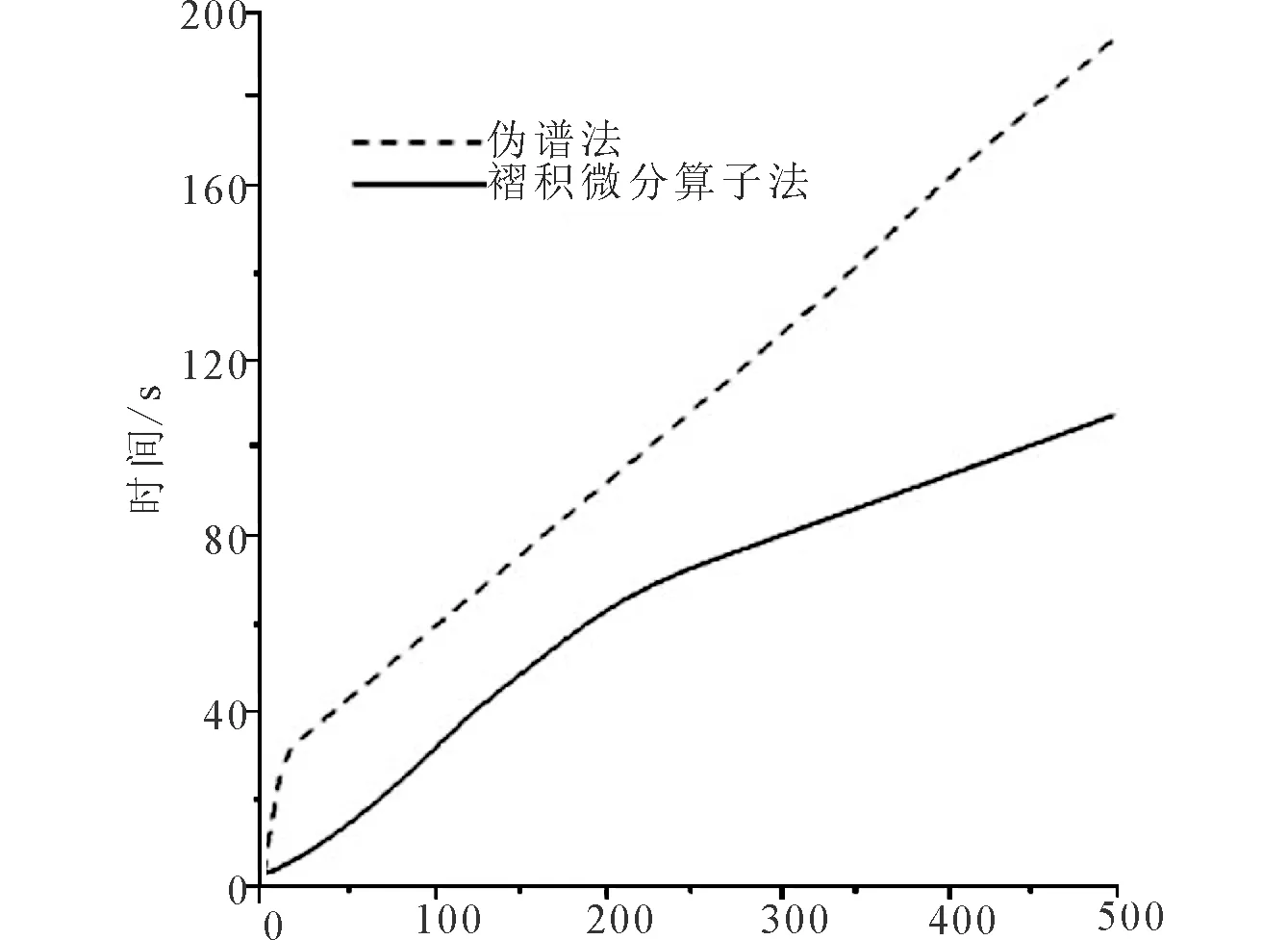
圖4 褶積微分算子法與偽譜法計(jì)算耗時比較Fig.4 Time-consuming comparison of calculating by the convolution differentiator method and pseudo-spectral method

4.2 Marmousi經(jīng)典模型

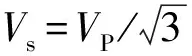
圖5(a)為原始Marmousi速度模型示意圖，圖5(b)、(c)分別是利用褶積微分算子法和偽譜法得到的波場快照。從波場快照來看，震源發(fā)出的地震波在介質(zhì)界面和突變點(diǎn)處產(chǎn)生的反射和繞射等現(xiàn)象非常明顯，并且兩種方法得到的波場快照的頻散程度基本相當(dāng)。說明基于Forsyte廣義正交多項(xiàng)式褶積微分算子法的地震數(shù)值模擬方法可以很好地模擬地震波在速度變化比較劇烈的介質(zhì)中的傳播。

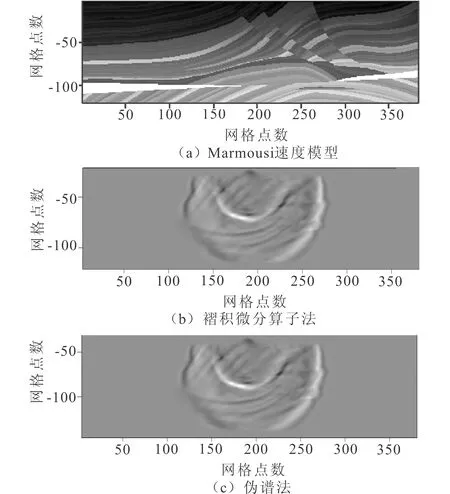
圖5 Marmousi速度模型及某時刻的波場快照Fig.5 The Marmousi velocity model and wave field snapshot at a given time

圖6所示為褶積微分算子法與經(jīng)典偽譜法原始Marmousi模型同一點(diǎn)地震圖的比較。從圖中可以看出，除了振幅有微小的差別外，相位基本上一致，這也從另一個側(cè)面說明了褶積微分算子法的有效性。

4.3 各向異性介質(zhì)模型

采用Thomsen[30]選出的實(shí)際頁巖巖樣作為檢驗(yàn)?zāi)Ｐ汀ＤＰ途W(wǎng)格大小為128×128，網(wǎng)格空間步長為10 m，時間步長為1 ms，震源為主頻20 Hz的Ricker子波，位置位于介質(zhì)的中心位置。介質(zhì)的彈性參數(shù)見表2。

表2 各向異性介質(zhì)模型參數(shù)

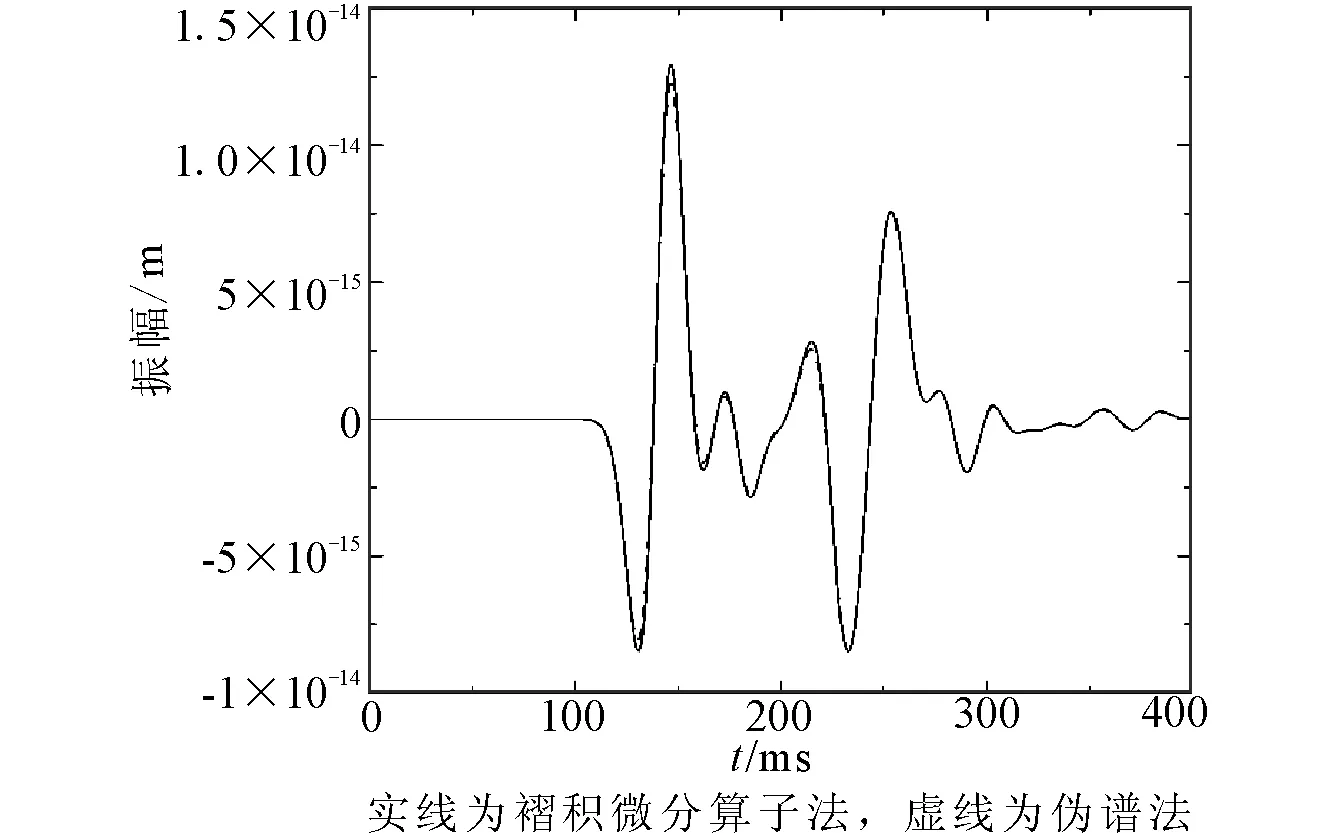
圖6 褶積微分算子法與經(jīng)典偽譜法原始 Marmousi 模型同一點(diǎn)振動圖的比較Fig.6 Comparison of vibration at the same point of original Marmousi model using the convolutional differentiator method and psendo-spectra method

圖7 各向異性頁巖介質(zhì)中的波場快照Fig.7 Snapshot of wave field in anisotropic shale media

比較二者的波場快照(圖7)可以發(fā)現(xiàn)，二者的頻散效應(yīng)基本相當(dāng)。兩種方法得到的波場快照都清晰地刻畫了波前面的形態(tài)。我們知道，各向異性介質(zhì)模型中的波場傳播特征對確定地層構(gòu)造特征和類型具有重要的理論意義與應(yīng)用前景。

5 與偽譜法的計(jì)算時間理論分析及與有限差分法及偽譜法的理論精度分析

5.1 與偽譜法的計(jì)算時間理論分析

假設(shè)二維空間計(jì)算區(qū)域的大小為N×N，褶積微分算子的長度為M。對聲波方程進(jìn)行數(shù)值計(jì)算時，使用偽譜法需要(N2log2N)次復(fù)數(shù)乘法；使用褶積微分算子法只需要M×N2次實(shí)數(shù)乘法。顯然兩者理論計(jì)算時間比為M/(4log2N)，只要M<(4log2N)，則褶積微分算子法將比偽譜法的計(jì)算速度快[25]。

5.2 與有限差分法及偽譜法的理論精度分析

在波動方程基礎(chǔ)上，檢驗(yàn)數(shù)值模擬方法準(zhǔn)確性的最精確實(shí)驗(yàn)是均勻介質(zhì)中脈沖響應(yīng)的計(jì)算，因?yàn)樵跀?shù)值計(jì)算中單脈沖能夠產(chǎn)生最寬的頻段。Zhou等[25，31]分別計(jì)算了不同方案所對應(yīng)的零炮檢距脈沖響應(yīng)，計(jì)算結(jié)果表明，偽譜法可以產(chǎn)生很好的效果，子波延續(xù)時間很短，并且沒有二次擾動；四階有限差分法的準(zhǔn)確性要相對差一點(diǎn)，子波開始時是正確的，但由于網(wǎng)格頻散，子波延續(xù)時間長，并且有二次擾動產(chǎn)生。九點(diǎn)褶積微分算子法計(jì)算結(jié)果接近于偽譜法，比四階有限差分法要好得多[28]。

6 結(jié)論

本文所使用的方法是將褶積微分算子應(yīng)用于地震波場數(shù)值模擬的又一次成功嘗試。通過引入高斯窗函數(shù)，較大程度地壓制了算子截?cái)嘁鸬募账剐?yīng)。三種不同地質(zhì)模型理論計(jì)算結(jié)果表明，該方法計(jì)算速度快，精度高，是繼戴志陽[27]發(fā)展的褶積微分算子法之后的又一種彈性波數(shù)值計(jì)算的有效工具。將本方法與偽譜法進(jìn)行比較，發(fā)現(xiàn)本文的褶積微分算子法對數(shù)值頻散的抑制能力與偽譜法相當(dāng)，但計(jì)算時間明顯占據(jù)優(yōu)勢，可以更高效地模擬地震波在復(fù)雜介質(zhì)中的傳播過程。

)

[1]ChapmanCH，ShearerPM.RayTracinginAzimuthallyAnisotropicMedia-Ⅱ ——Quasi-shearWaveCoupling[J].GeophysicalJournalInternational，1989，96(1)：65-83.

[2] Li Y G，Leary P C，Aki K.Seismic Ray Tracing for VSP Observations in Homogeneous Fractured Rock at Oroviue[J].EOS Transaction America Geophysical Union，1986，67(44)：1117.

[3] Cerveny V，F(xiàn)irbas P.Numerical Modeling and Inversion of Travel Times of Seismic Body Waves in Inhomogeneous Anisotropic Media[J].Science & Mathematic Geophysical Journal International，1984，76(1)：41-51.

[4] Pao Y H，Varatharajulu V.Huygen’s Principle Radiation Conditions and Integral Formulas for the Scattering of Elastic Waves[J].The Journal of the Acoustical Society of America，1976，59(6)：1361-1371.

[5] Bouchon M.Diffraction of Elastic Waves by Cracks or Cavities Using the Discrete Wave Number Method[J].The Journal of the Acoustical Society of America，1987，81：1671-1676.

[6] Fu L Y，Bouchon M.Discrete Wavenumber Solutions to Numerical Wave Propagation in Piecewise Heterogeneous Media-Ⅰ——Theory of Two-dimensional SH Case[J].Geophysical Journal International，2004，157：481-498..

[7] Alterman Z，Karal C.Propagation of Seismic Waves in Layered Media by Finite Difference Methods[J].Bulletin of the Seismological Society of America，1968，58(1)：367-398..

[8] Virieux J.S H Wave Propagation in Heterogeneous Media：Velocity-stress Finite Difference Method[J].Geophysics，1984，49(11)：1933-1957.

[9] Virieux J，P-SV Wave Propagation in Heterogeneous Media：Velocity-stress Finite-difference Method：Shear Waves[J].Geophysics，1986，51(4)： 889-901.

[10] Oprsal I，Zahradnik J.Elastic Finite Difference Method for Irregular Grids[J].Geophysics，1999，64(1)：240-250.

[11] Carcione J M，Herman G C，Kroode A P E.Seismic Modeling[J].Geophysics，2002，67(4)：1304-1325.

[12] 嚴(yán)武建，王彥賓，石玉成.基于偽譜和有限差分混合方法的蘭州盆地強(qiáng)地面運(yùn)動二維數(shù)值模擬[J].地震工程學(xué)報(bào)，35(2)：302-310.YAN Wu-jian，WANG Yan-bin，SHI Yu-cheng.2D Simulation of the Strong Ground Motion in Lanzhou Basin with Hybrid PSM/FDM Method[J].Northwestern Seismological Journal，2013，35(2)：302-310.(in Chinese)

[13] Gazdag J.Modeling of the Acoustic Wave Equation with Transform Method[J].Geophysics，1981，46：854.

[14] Kosloff D，Baysal E.Forward Modeling by a Fourier Method[J].Geophysics，1982，47(10)：1402-1412.

[15] Kosloff D，Reshef M，Loewenthal D.Elastic Wave Calculation by the Fourier Method[J].Bulletin of the Seismological Society of America，1984，74(3)：875-891.

[16] Fornberg B.The Pseudo-spectral Method：Comparisons with Finite Differences for the Elastic Wave Equation[J].Geophysics，1987，52(4)：483-501.

[17] Reshef M，Kosloff D.Applications of Elastic Forward Modeling to Seismic Interpretation[J].Geophysics，1985，50：1266-1272.

[18] 周輝，徐世浙，劉斌，等.各向異性介質(zhì)中波動方程有限元法模擬及其穩(wěn)定性[J].地球物理學(xué)報(bào)，1997，40(6)：833-841.ZHOU Hui，XI Shi-zhe，LIU Bin，et a1.Modeling of Wave Equations in Anisotropic in Anisotropic Media Using Finite Element Method and Its Stability Condition[J].Chinese Journal of Geophysics，1997，40(6)：833-841.(in Chinese)

[19] 張美根，王妙月，李小凡，等.各向異性彈性波場的有限元數(shù)值模擬[J].地球物理學(xué)進(jìn)展，2002，17(3)：384-389，413.ZHANG Mei-gen，WANG Miao-yue，LI Xiao-fan，et a1.Finite Element Forward Modeling of Anisotropic Elastic Waves[J].Progress in Geophysics，2002，17(3)：384-389，413.(in Chinese)

[20] Komatitsc D，Tromp J.Introduction to the Spectral-element Method for 3-D Seismic Wave Propagation[J].Geophysical Journal International，1999，139(3)：806-822.

[21] Komatitsch D，Ritsema J，Tromp J.The Spectral-element Method，Beowulf Computing and Global Seismology [J].Science，2002，298(29)：1737-1742.

[22] Sinclair C，Greenhalgh S，Zhou B.2.5-D Modeling of Elastic Waves in Anisotropic Media Using the Spectral-element Method——a Preliminary Investigation[C]//AESC，Melbourne，Australia，2006.

[23] 李幼銘，胡健行.細(xì)胞自動機(jī)在地震波傳播中的應(yīng)用[J].地球物理學(xué)報(bào)，1995，38(5)：651-661.LI You-ming，HU JIAN-XING.Application of Cellijlar Automata Approach to the Study of Seismic Wave Propagation[J].Chinese Journal Geophysics，1995，38(5)：651-661.(in Chinese)

[24] 羅明秋，劉洪，李幼銘.地震波傳播的哈密頓表述及辛幾何算法[J].地球物理學(xué)報(bào)，2001，44(1)：120-128.LUO Ming-qiu，LIU Hong，LI You-ming.Hamiltonian Description and Symplectic Method of Seismic Wave Propagation[J].Chinese Journal Geophysics，2001，44(1)：120-128.(in Chinese).

[25] Zhou B，Greenhalgh S A，Zhe J.Numerical Seismogram Computations for Inhomegeneous Media Using a Short，Variable Length Convolutional Differentiator[J].Geophysical Prospecting，1993，41(6)：751-766..

[26] 張中杰，滕吉文，楊頂輝，等,聲波與彈性波場數(shù)值模擬中的褶積微分算子法[J].地震學(xué)報(bào)，1996，18(1)：60-69.ZHANG Zhong-jie，TENG Ji-wen，YANG Dang-hui.Acoustic and Elastic Wave Modeling by a Convolutional Differentiator[J].Acta Seismoligica Sinica，1996，18(1)：63-69.(in Chinese)

[27] 戴志陽，孫建國，查顯杰.地震波場模擬中的褶積微分算子法[J].吉林大學(xué)學(xué)報(bào)：地球科學(xué)版，2005，35(4)： 520-524.DAI Zhi-yang，SUN Jian-guo，CHA Xian-jie.Seismic Wave Field Modeling with Convolutional Differentiator Algorithm[J].Journal of Jilin Unviersity：Earth Science Edition，2005，35(4)：520-524.(in Chinese)

[28] 戴志陽，孫建國，查顯杰.地震波混合階褶積算法模擬[J].物探化探計(jì)算技術(shù)，2005，27(2)：111-114.DAI Zhi-yang，SUN Jian-guo，CHA Xian-jie.Seismic wave Field Modeling With Hybrid Order Convolution Differentiator[J].Computing Techniques for Geophysics and Geochem ical Exploration，2005，27(2)：111-114.(in Chinese)

[29] 謝靖.物探數(shù)據(jù)處理的數(shù)學(xué)方法[M].北京：地質(zhì)出版社，1981，97-104.XIE Jing.Numerical Method for Geophysical Data-process[M].Beijing：Geological Publishing House，1981：97-104.

[30] Thomsen L.Weak-elastic Anisotropy[M].Geophysics，1986，51(10)：1954-1996.

[31] Zhou B，Greenhalgh S A.Seismic Scalar wave Equation Modeling by a Convolutional Differentiator[J].Bulletin of the Seismological Society of America，1992，82(1)：289-303.

[32] 賀同江，劉紅艷，李小凡.粘彈性介質(zhì)地震波傳播的褶積微分算子法數(shù)值模擬研究[J].西北地震學(xué)報(bào)，2010，32(4)318-324.HE Tong-jiang，LIU Hong-yan，LI Xiao-fan.Numerical Simulation of Seismic Wave Propagation in Viscous-elastic Media by the Convolutional Differentiator Method[J].Northwestern Seismological Journal，2010，32(4)：318-324.(in Chinese)

[33] 劉少林，李小凡，汪文帥，等.最優(yōu)化辛格式廣義離散奇異核褶積微分算子地震波場模擬[J].地球物理學(xué)報(bào)，2013，56(7)：2452-2462.LIU Shao-lin，LI Xiao-fan，WANG Wen-shuai，et al.Optimal Symplectic Scheme and Generalized Discrete Convolutional Differentiator for Seismic Wave Modeling[J].Chinese Journal Geophysics，2013，56(7)：2452-2462.(in Chinese)

[34] 李一瓊，李小凡，朱童.基于辛格式奇異核褶積微分算子的地震標(biāo)量波場模擬[J].地球物理學(xué)報(bào)，2011，54(7)：1827-1834.LI Yi-qiong，LI Xiao-fan，ZHU Tong.The Seismic Scalar wave Field Modeling by Symplectic Scheme and Singular Kernel Convolutional Differentiator[J].Chinese Journal Geophysics，2011，54(7)：1827-1834.(in Chinese)

[35] 龍桂華，李小凡，張美根.基于Shannon奇異核理論的褶積微分算子在地震波場模擬中的應(yīng)用[J].地球物理學(xué)報(bào)，2009，52(4)：1014-1024.LONG Gui-hua，LI Xiao-fan，ZHANG Mei-gen.The Application of Convolutional Differentiator in Seismic Modeling Based on Shannon Singular Kernel Theory[J].Chinese Journal Geophysics，2009，52(4)：1014-1024.(in Chinese)

Comparison of Convolutional Differentiator Method and the Pseudo-spectral Method Used in Seismic Wave Simulation

LIU Hong-yan， CHEN Yu-kun， LIU Fang

(EarthquakeAdministrationofTianjinMunicipality,Tianjin300201，China)

This study employed the convolutional differentiator seismic simulation method constructed using Forsyte polynomials to simulate the seismic wave propagation in a complex heterogeneous media and compared the simulation results to those obtained from the pseudo-spectral method.By comparing the computational time of the pseudo-spectral and convolutional differentiator methods，it was found that the computing time of the convolutional differentiator method is always less than that of pseudo-spectral method when the same computing environment is employed.Consequently，the convolutional differentiator seismic simulation method has an advantage in this regard.By comparing the snapshots obtained using the above mentioned methods，it was found that the dispersion of the snapshots by the convolutional differentiator is similar to that obtained by the pseudo-spectral method，which constituted another advantage for the convolutional differentiator method for seismic wave numerical simulation.Overall，the convolutional differentiator method is a viable alternative for seismic wave propagation simulation.

convolutional differentiator； pseudo-spectral method； seismic wave propagation； numerical simulation

2015-04-01

金基項(xiàng)目：地震科技星火計(jì)劃項(xiàng)目(XH13002)．

劉紅艷(1983-)，女，工程師，主要從事地震活動性、工程地震、復(fù)雜介質(zhì)的地震波場數(shù)值模擬研究等工作.E-mail：liuhongyan_012@163.com

P315； P631.4

A

1000-0844(2015)02-0594-07

10.3969/j.issn.1000-0844.2015.02.0594