平方根形式的CKF/后向平滑非線性濾波研究
湯霞清, 黃湘遠, 武 萌, 張 環
(裝甲兵工程學院控制工程系,北京 100072)
平方根形式的CKF/后向平滑非線性濾波研究
湯霞清, 黃湘遠, 武 萌, 張 環
(裝甲兵工程學院控制工程系,北京 100072)
為了提高非線性濾波的精度、數值穩定性并保證計算速度,將非線性平方根后向平滑 (Square Root Backward Smoothing, SR-BS) 算法和平方根容積卡爾曼濾波(Square Root Cubature Kalman Filter, SR-CKF)引入到前向濾波-后向平滑-前向濾波的濾波框架中,形成平方根形式的CKF/后向平滑(SR-BS-CKF)非線性濾波算法。該算法在首次前向濾波的基礎上利用后向平滑-前向濾波的思想來提高濾波精度,利用平方根更新來保證濾波的數值穩定性;該算法包含2次SR-CKF和1次SR-BS運算,由于SR-BS計算量較小,因此該算法計算量為SR-CKF的2倍左右,增加不大。仿真結果表明:SR-BS-CKF算法濾波精度高,數值穩定性強,計算速度較快,濾波性能優于CKF。
容積卡爾曼濾波;非線性后向平滑;平方根濾波;濾波性能
基于量測信息和系統方程的最優估計理論在導航、信息處理、金融等領域獲得了大量的應用。根據利用的量測信息的時間區別,可分為預測、濾波和平滑3種[1]。
濾波是利用當前時刻以及以前的量測信息對當前狀態進行估計,典型算法有卡爾曼濾波及其非線性形式,如:擴展卡爾曼濾波(Extended Kalman Filter,EKF)、無損卡爾曼濾波(Unscented Kalman Filter,UKF)、容積卡爾曼濾波(Cubature Kalman Fiter, CKF)等[2]。CKF是一種計算量小、精度高的非線性濾波算法,能夠實現任意高斯非線性系統的狀態估計[3-4]。平方根CKF (Square Root CKF, SR-CKF)利用平方根矩陣代替協方差矩陣,降低計算機字長限制對數據處理精度的影響,避免協方差矩陣Cholesky分解,提高了算法的數值穩定性[5]。
平滑是一種離線處理算法,其利用以前、當前、以后的量測信息進行狀態估計,估計精度理論上優于濾波。基于線性狀態的平滑算法[6-7]已經獲得了大量應用,而基于非線性狀態的平滑算法[8-9]應用還較少。
為了提高濾波精度,曹意等[10]將非線性濾波和線性平滑結合起來,形成多次迭代和窗口平滑算法;霍光等[11]在此基礎上,從計算量和濾波精度考慮,提出了后向平滑CKF (Backward Smoothing CKF, BS-CKF)算法。以上2種算法的本質依然是濾波算法,而不是平滑算法,只是借用了平滑算法的思想;而且2種算法均基于線性狀態方程推導,具有一定的局限性。
為了提高非線性狀態的濾波精度,本文重新推導了非線性狀態的后向平滑算法,提出了平方根形式的后向平滑算法(Square Root Backward Smoothing,SR-BS),將SR-CKF和SR-BS算法引入到前向濾波-后向平滑-前向濾波框架[10]中,形成SR-BS-CKF非線性濾波算法,最后通過仿真試驗對該算法進行驗證。
1 平方根容積卡爾曼濾波
非線性濾波就是基于非線性系統方程,根據當前及此前的觀測量序列估計出當前系統狀態。考慮如下離散非線性系統:
(1)
式中:xk和zk分別為k時刻系統的狀態量和觀測量;f(·)和h(·)為已知任意函數;系統噪聲wk~N(wk;0,Qk),其中Qk為系統噪聲方差矩陣;觀測噪聲vk~N(vk;0,Rk),其中Rk為觀測噪聲方差矩陣,且wk和vk互相獨立。

1.1 球面徑向容積規則

I(f)=∫Rnf(x)exp(-xTx)dx。
(2)
式中:Rn為積分區域。
取x=ry,yTy=1,r∈[0,∞),積分式I(f)在Spherical-radial坐標系可寫成

(3)
式中:Un為n維單位球面;σ(·)為Un上的元素。
積分I(f)可分離為球面積分S(r)和徑向積分R,其中:
S(r)=∫Unf(ry)dσ(y);

三階球面徑向容積規則由三階球面規則和一階徑向規則組成[3],基本思路是分別對S(r)和R進行多項式逼近,利用兩者的逼近方式對積分I(f)進行逼近。對于高斯分布x~N(x;μ,Σ),I(f)的三階近似規則為

(4)

CKF采用球面徑向容積規則和Guass-Bayes濾波框架,利用2n個等權值的容積點來實現非線性積分的多項式逼近,避免了非線性模型的線性化,能夠實現任意高斯非線性系統的狀態估計,濾波精度達到三階。
1.2 平方根濾波算法
常規CKF需對Pk-1和Pk|k-1進行Cholesky分解,這是一項計算量大且非常危險的工作。因為受計算機字長有限、初始矩陣P0設置不當等因素的影響,Pk-1和Pk|k-1易失去正定性,Cholesky分解無法進行,導致濾波精度急劇下降甚至濾波發散。SR-CKF是一種有效的解決方法,其降低了計算機字長限制對數據處理精度的影響,提高了算法的數值穩定性[4-5]。
1.2.1 時間更新



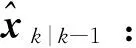



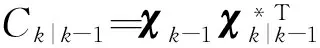

1.2.2 量測更新
1) 重采樣及觀測傳播:

zi,k|k-1=h(xi,k|k-1)。


3) 計算Pzz的均方根Szz和Pxz:



4) 估計濾波增益陣,最優估計及協方差陣:
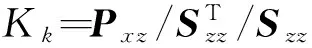


2 非線性平方根后向平滑算法
2.1 非線性狀態后向平滑算法
后向平滑算法根據當前及此前的觀測量序列及前向濾波獲得的最優狀態估計序列進行后向遞推,來獲得此前任意時刻狀態的最優估計。后向平滑分為固定區間平滑、固定點平滑和固定滯后平滑[10]。三者之間沒有本質的區別,主要區別在于針對的對象不同。基于線性系統的平滑算法結構簡單、易于實現,獲得了較多的應用。

首先,本文不加證明地給出定理1[9]。
定理1:設x、a、b是3個具有前二階矩的隨機矢量,令z=[ab],則x基于z的最優估計為

(5)



(6)

(7)

將式(6)、(7)分別改寫為如下形式:
(8)


將式(10)代入式(8),由于Pk|k-1和Ck|k-1理論上均為可逆正定矩陣,則有

(11)
則k到k-1時刻的一步后向平滑狀態為

(12)



(13)

協方差陣Pk-1|k為

(14)


(15)
由式(12)、(15)構成了非線性系統的一步后向平滑算法。
2.2 平方根后向平滑算法(SR-BS)
前文推導了非線性狀態前向濾波的平方根算法和后向一步平滑算法,為了將兩者結合起來,需推導后向平滑的平方根算法。
首先考慮濾波增益陣Wk的平方根算法,即

(16)
考慮到Pk|k-1為對稱正定陣,則有

(17)
從而獲得

(18)
將式(18)代入式(15),可得

(19)
可得Pk-1|k的平方根矩陣Sk-1|k為

(20)
3 CKF/后向平滑非線性濾波
3.1 前向濾波-后向平滑-前向濾波
前向濾波是一種實時狀態估計方法,后向平滑過程是一種精度優于前向濾波的事后狀態估計方法,因為前向濾波能夠消除大部分誤差,經后向平滑后再次前向濾波可進一步消除誤差,兩者結合起來可獲得一種高精度的實時濾波方法。曹意等[10]推導了UKF和線性平滑的多次迭代和窗口平滑濾波算法,證明了2種方案均能夠提高估計精度,但是濾波精度并不一定隨著迭代次數或窗口長度的增加而增加。

圖1 濾波算法基本框架
3.2 平方根形式的CKF/后向平滑濾波算法
霍光等[11]基于線性狀態方程設計了CKF/后向平滑濾波器,本文在此基礎上考慮到SR-CKF和SR-BS的強數值穩定性,以及對非線性狀態的適用性,將兩者引入到前向濾波-后向平滑-前向濾波框架中,形成平方根形式的CKF/后向平滑非線性濾波器(SR-BS-CKF),實現任意高斯非線性模型的高精度實時濾波。基本濾波框架如下:



4 仿真實驗
考慮一個典型的飛行器控制問題[4],其非線性離散方程為


(21)


x0=(1 000 m,300 m/s,1 000 m,0 m/s,-3°/s)T,

10 mrad/s)]2。

(22)
圖2給出了200次仿真實驗的位置、速度、角速度的RMSE曲線,考慮到濾波器穩定時間,只給出了50~100 s的誤差曲線。圖2表明:2種算法均能對狀態進行有效估計,SR-BS-CKF的估計精度高于SR-CKF,其中位置估計體現得最明顯,速度估計次之,角速度估計相差不大。表1給出了2種算法后50 s位置、速度和角速度的RMSE平均值,經計算可知:SR-BS-CKF算法的位置、速度和角速度估計精度比SR-CKF算法分別提高了10%、4%、1%左右,表明SR-BS-CKF算法對提高濾波精度有效。

圖2 2種濾波算法的RMSE曲線對比
表1 2種濾波算法的RMSE均值

濾波算法位置/m速度/(m·s-1)角速度/((°)·s-1)SR-CKF24.978914.09391.4096SR-BS-CKF22.910913.61391.4018
表2給出了一次仿真實驗(100 s)2種濾波算法的運算時間,可以看出:SR-BS-CKF所用時間為SR-CKF的2~3倍。因為每次濾波過程中,SR-BS-CKF需進行2次SR-CKF及1次SR-BS操作,而SR-BS的計算量相對SR-CKF較小,因此濾波運算主要集中在2次SR-CKF操作上。試驗結果表明:SR-BS-CKF算法的計算量相對于SR-CKF算法增長不大,濾波實時性的實現并不是非常困難。

表2 2種濾波算法的運算時間
5 結論
為了提高CKF的濾波精度和數值穩定性并保證濾波實時性,本文將SR-BS、SR-CKF引入到前向濾波-后向平滑-前向濾波的框架中,形成了一種新的非線性濾波,能夠適用于任何高斯非線性系統。為了進一步提高濾波精度,有以下3種可能的方式:1) 利用高階非線性濾波代替常規CKF;2) 使用“多步后向平滑-前向濾波”的框架;3) 進行多次“一步后向平滑-前向濾波”,形成迭代算法。高精度的濾波方式必然帶來較大的計算量,影響濾波的實時性,如何在兩者之間找到一個平衡點需進一步研究。
[1] 宮曉琳,張蓉,房建成. 固定區間平滑算法及其在組合導航系統中的應用[J]. 中國慣性技術學報,2012,20(6):687-693.
[2] 王小旭,潘泉,黃鶴,等. 非線性系統確定采樣型濾波算法綜述[J]. 控制與決策,2012,27(6):801-812.
[3] Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman Filtering for Continuous-discrete Systems: Theory and Simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993.
[4] Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.
[5] 郝燕玲,楊峻巍,陳亮,等.基于SRCKF的水下航行器動基座初始對準技術[J]. 華中科技大學學報:自然科學版,2012,40(2):123-127.
[6] 康泰鐘,鐘麥英,李建利. 基于時間雙向解算融合的POS事后處理算法[J]. 儀器儀表學報,2012,33(9):2067-2072.
[7] 秦顯平,楊元喜.平方根濾波/平滑/雙向濾波在LEO星載GPS定軌中的應用[J]. 武漢大學學報:信息科學版,2009,34(10): 1176-1180.
[8] Simo S. Unscented Rauch-Tung-Striebel Smoother[J]. IEEE Transactions on Automatic Control, 2008,53(3):845-849.
[9] Wang X X, Pan Q, Liang Y, et al. Application of Unscented Transformation for Nonlinear State Smoothing [J]. Acta Automatica Sinica, 2012,38(7):1097-1101.
[10] 曹意,茅旭初.基于非線性濾波和平滑相迭代的GPS定位估計算法[J]. 上海交通大學學報,2009,43(7):1108-1112.
[11] 霍光,李冬梅. 基于后向平滑容積卡爾曼濾波的單站無源定位算法[J]. 信號處理,2013,29(1):68-74.
[12] Ito K, Xiong K Q. Gaussian Filter for Nonlinear Filtering Problem[J]. IEEE Transactions on Automatic Control, 2000, 45(5):910- 927.
(責任編輯:尚彩娟)
Research on Square Root CKF/Backward Smoothing Nonlinear Filter
TANG Xia-qing, HUANG Xiang-yuan, WU Meng, ZHANG Huan
(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)
In order to achieve higher precision and stronger numeric stability and an efficient computation, the paper introduces nonlinear Square Root Backward Smoothing (SR-BS) algorithm and Square Root Cubature Kalman Filter (SR-CKF) into the framework of forward filtering-backward smoothing-forward filtering, so as to form square root CKF/BS nonlinear filter (SR-BS-CKF) algorithm. The algorithm utilizes backward smoothing-forward filtering based on the first forward filtering to improve the accuracy. It ensures the stability of the filter values by using square root updating method. The algorithm contains two SR-CKF operations and one SR-BS operation, because SR-BS has the low calculating amount, the calculation amount of the algorithm approximately equals to two times of SR-CKF and increases slightly. The simulation results indicate that the algorithm SR-BS-CKF has high precision, stronger numerical stability and rapid calculating speed, which has more effective filter performance than CKF.
Cubature Kalman Filter (CKF); nonlinear backward smoothing; square root filter; filter performance
1672-1497(2015)02-0065-05
2014-11-20
軍隊科研計劃項目
湯霞清(1965-),男,教授,博士。
TN713
A
10.3969/j.issn.1672-1497.2015.02.013

