主動再制造產品設計參數與服役特性的映射關系

□ 宋守許 □ 鄢子超 □ 劉云東

合肥工業大學 機械與汽車工程學院 合肥 230009

再制造是以產品全壽命周期理論為指導，對廢舊產品進行回收，利用技術手段進行修復和改造廢舊產品的一系列技術措施或工程活動的總稱［1］。伴隨著再制造工程在各行各業的開展，其基礎理論及應用得到了長足的發展［2-6］。近年來，針對再制造毛坯的不確定性問題，國內學者提出了主動再制造的理念。主動再制造是指在整個生命周期過程中，存在著某段時間是再制造最佳時間段，在這段時間內主動地選取最優再制造方式，使再制造達到最佳效果［7-11］。

目前，主動再制造的相關理論研究尚處于初始階段，其研究成果體現在兩個方面：一是主動再制造設計方法［9、10］；二是主動再制造時間區域抉擇方法［7］。 雖然相關理論成果還不是很多，卻為主動再制造的進一步發展奠定了基礎;同時，主動再制造理念的提出，為再制造工程的發展開啟了另一扇大門，使再制造由被動轉為主動。按照現有主動再制造時間區域的判定理論，在產品確定以后，產品的主動再制造時間區域是確定的、不可調控的［7］，但為了更好地體現主動再制造的主動性，僅僅確定產品的再制造時間區域是不夠的，若能通過設計參數的調整，實現產品再制造時間區域的主動調控，從而降低再制造毛坯的不確定性，使其在產品整個生命周期內的經濟、技術、環境等指標達到最佳，對真正實現產品主動再制造具有重大實際意義。

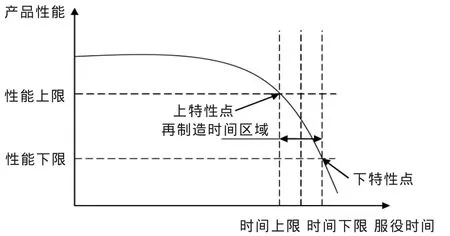
▲圖1 產品的服役特性曲線

1 產品主動再制造的主動調控機制

在分析產品主動再制造的調控機制前，需明確產品主動再制造時間區域如何確定，以及產品服役特性的概念。通常產品的性能隨著服役時間的增加而逐漸降低，通過一定的評價方法，可以確定再制造產品性能的上限和下限，在產品性能上限和下限之間的時間段，即為再制造時間區域，如圖1所示。產品的服役特性是指產品性能隨服役時間的變化規律，其中產品的性能是指產品的強度、功率、疲勞壽命等，圖1中產品性能隨服役時間的變化曲線即為產品的服役特性曲線。在服役環境等外界條件不變的情況下，產品設計參數對產品性能起著決定性的作用［12-15］，因此，通過調整產品設計參數來改變產品性能，可實現對產品服役特性的調控。

對產品服役特性進行調整，就必須對產品的設計參數進行優化；同時，產品的加工工藝等也需要進行相應的調整，而產品主動再制造時間區域是通過對產品性能以及再制造經濟、技術、環境等指標的綜合評價來確定的。因此產品主動再制造的主動調控機制可以概述為：通過優化產品設計參數達到依據經濟、技術、環境等指標確定的最優服役特性，在此基礎上按照一定的評價方法，主動確定產品的最佳再制造時間區域。通過優化設計參數使產品服役特性最優是實現產品再制造主動調控的關鍵，而建立產品設計參數與服役特性映射關系是實現這一過程的基礎。

2 產品設計參數與服役特性映射模型

2.1 產品設計參數與服役特性映射關系的建模流程

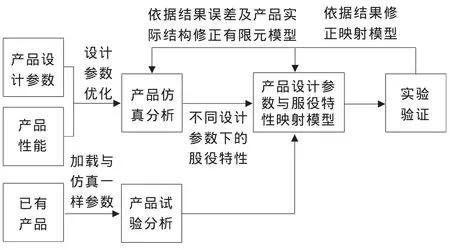
▲圖2 產品設計參數與服役特性映射關系的建模流程

為了建立產品設計參數與服役特性的映射關系，需要明確產品設計參數的變化對服役特性的影響。用實驗的方法逐一研究每項設計參數與服役特性的映射關系，將需要花費大量的人力、物力，且短時間內很難完成。因此，選取產品設計參數及性能，以設計參數為優化變量，對產品進行有限元分析，獲取相應的服役性能仿真結果；依據有限元分析結果建立設計參數與服役特性的映射模型；最后通過對已有產品的實驗分析，驗證所建模型的正確性，并依據驗證的結果，對仿真模型、仿真過程及實驗過程進行檢查和修正。具體建模流程如圖2所示，其中，設計參數主要根據產品的結構、性能等選取，產品性能主要根據其對產品再制造時間區域的影響大小進行選取。

2.2 產品設計參數與服役特性映射模型的建立

建立產品設計參數與服役特性之間的映射模型，實質上是建立產品性能與服役時間及設計參數之間的關系，這種關系可用一系列空間直角坐標系表示，一個空間直角坐標系表示一個設計參數與一項服役特性之間的關系。應用控制變量法研究產品設計參數與服役特性之間的映射關系，將產品的服役時間n等分，并以產品設計參數為自變量，通過產品的仿真分析，得到性能在每個時間節點處變化的規律，從而建立選定的設計參數與服役特性之間的關系。通過仿真方法獲得了產品設計參數與服役性能的相關數據，在此基礎上，采用最小二乘法擬合二者的曲線函數，其擬合曲線的基函數根據數據點的分布規律選定。

在某一個服役時間節點ti（i=1,2,3…）處，根據多項式擬合的最小二乘法，產品某項服役性能 F（ti，i）與某項設計參數xi之間的關系可表示為：

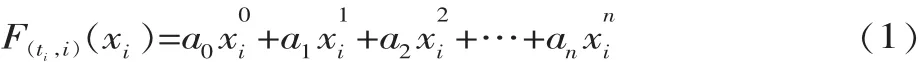
由式（1）依次建立產品設計參數xi與多項服役性能之間的關系，具體表達式為：

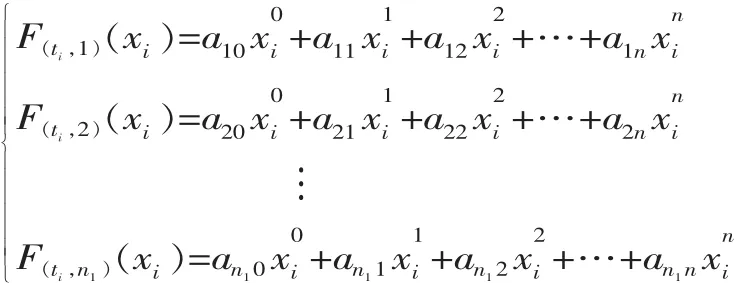
式中：n1表示共選定了n1（n1=1,2,3…）個產品服役性能。

上述方程組用矩陣形式表示為：

令：向量 α（ti，i）=［F（ti，1）（xi）F（ti，2）（xi）…F（ti，n1）（xi）］T，由于向量 α（ti，i）是選定的各項服役性能的集合，因此將其稱為產品服役性能向量，簡稱性能向量。

令：向量 β（ti，i）=［…］T，由于向量 β（ti，i）是由設計參數的n次冪組成的（n=1,2,3…），因此將其稱為產品設計參數向量，簡稱參數向量。

令 ：矩 陣 A（ti，i）=由 于 矩 陣 A（ti，i）是建立了產品設計參數與服役性能之間的關系，因此稱矩陣 A（ti，i）為產品服役性能的參數矩陣， 簡稱參數矩陣。

此時，產品設計參數xi與多項服役性能在服役時間節點ti處的函數關系表示為：

依據式（2），可以在服役時間節點ti處依次建立多個設計參數與多項服役特性之間的函數關系。若將服役時間節點ti處的產品多個設計參數與多項服役性能關系的集合用矩陣 F（ti，x）表示，其表達式為：

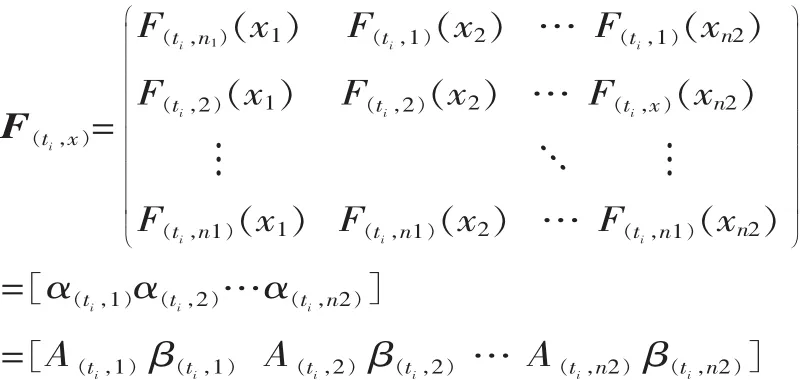
式中：n2表示共選定了n2個產品設計參數。

由于矩陣F（ti，x）是產品服役性能的集合，故稱F（ti，x）為產品服役性能矩陣，簡稱性能矩陣。

性能矩陣 F（ti，x）表達的是產品性能在某一服役時間節點ti隨設計參數變化的規律，而服役特性描述的是產品性能隨服役時間變化的規律，若將產品在每一服役節點處的性能矩陣用集合表示為：

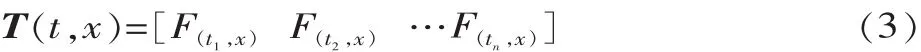
集合T包含了多項服役性能在每一服役節點處隨設計參數變化的規律，即為產品設計參數與服役特性的映射模型。

該映射模型的最大特點是它由一系列空間直角坐標系組成，這一特點十分有利于對產品主動再制造時間區域的主動調控，如前述圖1所示。從建立的設計參數與服役特性映射模型中輸入性能參數，可迅速查找到與前述性能的上限和下限相對應的所有設計參數，設計人員可根據經濟、技術、環境等指標，選擇合適的設計參數作為優化對象。

3 案例分析

為了驗證上述建模方法的可行性，以某車橋公司提供的HF15016系列橋殼為例進行實例驗證。

（1）橋殼設計參數的選取。常見的產品設計參數包括材料、尺寸、額定功率、額定載荷等，對于HF15016橋殼，其適配車型已經確定，因此，其額定載荷、輪距尺寸等設計參數無法更改，可以繼續優化的參數包括橋殼材料、橋殼體過渡圓角半徑、焊接工藝參數等。

（2）橋殼重要性能的選取。驅動車橋是汽車傳動系統中最末端的總成件，主要傳遞車架與車輪之間各個方向的作用力及扭矩；橋殼是驅動車橋的重要組成部分之一，其主要作用是承受汽車的載荷，因此橋殼的重要性能包括橋殼的強度、剛度、疲勞壽命等。

（3）橋殼有限元仿真分析。橋殼有限元仿真分析的主要任務是以橋殼設計參數為優化變量，對所選的橋殼性能在某時間節點處進行有限元仿真。運用Pro/E軟件建立橋殼的幾何模型，通過仿真軟件Workbench對橋殼進行分析。橋殼模型的相關參數為：材料牌號為510 L，彈性模量為218.9 GPa，泊松比為0.247，屈服極限為390 MPa；疲勞載荷的設置參照標準QC/T533.1999《汽車驅動橋臺架試驗方法》中的規定：最大載荷為150 kN（滿載負荷2.5倍），最小載荷為30 kN（滿載負荷的0.5倍），加載頻率為3 Hz，橋殼材料的S-N曲線通過實驗獲得；模型約束條件為：在橋殼的一端約束X、Y、Z 3個方向的軸向位移和繞Y、Z軸的轉動，在橋殼的另一端約束Y和Z方向的位移和繞Y、Z軸的轉動。

橋殼體在不同過渡圓角半徑下的疲勞壽命和強度的仿真結果見表1，圖3為橋殼過渡圓角半徑為17 mm時的應力云圖。

（4）建立橋殼設計參數與服役特性的映射模型。上述仿真對象的橋殼為新橋，所以建立模型的服役時間節點t1=0。根據式（1）再結合表1中的數據得到：

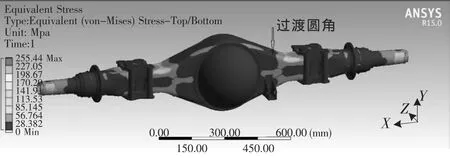
▲圖3 圓角半徑為17 mm的橋殼應力云圖

表1 橋殼在不同過渡圓角半徑下的疲勞壽命和強度分析結果

式中：x1為橋殼圓角半徑；F（t1，1）為疲勞壽命；F（t1，2）為強度。

通過式（4）得到性能向量 α（t1，1）=［F（t1，1）F（t1，2）］T，參 數 向 量 β（t1，1）=［x10x11］T， 參 數 矩 陣 A（t1，1）=所以橋殼過渡圓角半徑與疲勞壽命和強度在時間節點處的關系由式（2）得到：

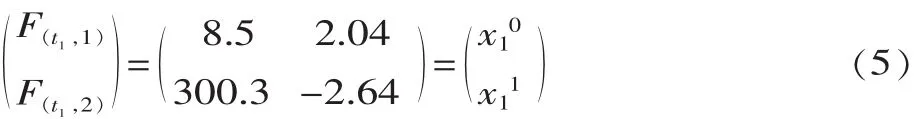
根據式（5）可以依次建立橋殼在不同服役時間節點時疲勞壽命和強度與橋殼過渡圓角半徑之間的函數關系，橋殼其它設計參數在每一服役時間節點處與其服役性能的關系也可按式（5）進行研究。

（5）試驗驗證。對R=20 mm的橋殼進行臺架試驗，如圖4所示。試驗過程與有限元仿真的參數設置為一致，橋殼臺架試驗的疲勞壽命結果為45.5萬次，將R=20 mm代入式（5），得到橋殼疲勞壽命為49.3萬次，兩者的誤差為7.71%［16-17］，可見上述提出的設計參數與服役特性映射模型的建模方法是可行的。

4 結論

（1）在分析產品主動再制造主動調控機制的基礎上，得到了優化產品設計參數是實現產品再制造主動調控的關鍵，通過優化設計參數可以實現產品的最優服役特性。

（2）建立了產品設計參數與服役特性之間的映射模型，實現了對產品主動再制造時間區域的主動調控。以橋殼為例，驗證了該模型的可行性。

▲圖4 橋殼臺架試驗

（3）該映射模型針對不同的產品具有普適性,但要建立完整的該模型是需要對不同產品各個時間節點處不同設計參數與服役性能的關系進行逐一研究。因此，后續工作將通過優化時間節點、設計參數及服役特性的選取來減輕有限元仿真和試驗的工作量。

［1］ 徐濱士.裝備再制造工程的理論與技術［M］.北京:國防工業出版社,2007.

［2］ 徐匡迪.工程師從物質財富的創造者到可持續發展的實踐者［J］.中國表面工程,2004,17（6）:1-6.

［3］ 王玉玲,孔銀響,吳保華,等.機械產品全生命周期再制造性評估［J］.機械設計與制造,2012（6）:266-268.

［4］ Du Yanbin,Cao Huajun,Liu Fei,et al.An Integrated Method for Evaluating the Remanufacturability of Used Machine Tool［J］.Journal of Cleaner Production,2012,20（1）:82-91.

［5］ Ijomah Winifred L,McMahon Christopher A,Hammond Geoffrey P,et al.Development of Design for Remanufacturing Guidelines to Support Sustainable Manufacturing ［J］.Robotics and Computer Integrated Manufacturing,2007,23（6）:712-719.

［6］ Shu Lily H,Flowers Woodie C.Application of a Design-forremanufacture Framework to the Selection of Product Lifecycle Fastening and Joining Methods ［J］．Robotics and Computer Integrated Manufacturing,1999，15（3）:179-190.

［7］ 劉濤.主動再制造時間區域決擇及調控方法研究 ［D］.合肥:合肥工業大學,2012.

［8］ 宋守許,劉明,柯慶鏑,等.基于強度冗余的零部件再制造優化設計方法［J］.機械工程學報,2013,49（9）:121-127.

［9］ 劉濤,劉光復,宋守許,等.面向主動再制造的產品可持續設計框架 ［J］.計算機集成制造系統,2011,17 （11）:2317-2323.

［10］劉濤,劉光復,宋守許,等.面向主動再制造的產品模塊化設計方法［J］.中國機械工程,2012,23（10）:1180-1187.

［11］劉光復,劉濤,柯慶鏑,等.基于博弈論及神經網絡的主動再制造時間區域抉擇方法研究 ［J］.機械工程學報,2013,49（7）:29-35.

［12］ Cao Ruiwu,ChengMing,Mi Chunting Chris,et al.Influence of leading Design Parameters on the Force Performance of a Complementary and Modular Linear Flux-Switching PermanentMagnetMotor ［J］.IEEE Transactionson Industrial Electronics,2014,61（5）:2165-2175.

［13］馬紅,賀錫鵬,鄭坊平,等.18-8型奧氏體不銹鋼鍋爐管服役特性研究（一）［J］.熱力發電,2011,41（1）:46-49.

［14］張衛華,李艷,宋冬利.高速列車運動穩定性設計方法研究［J］.西南交通大學學報,2013,48（1）:1-9.

［15］唐加福,汪定偉,劉士新,等.產品優化設計的用戶滿意模型［J］.管理科學學報,2003,6（3）:46-51.

［16］杜鳳山,王丹超,閆亮,等.2E12鋁合金中心孔板材疲勞壽命分析［J］.材料工程,2009,7（17）:58-66.

［17］李亮,宋健,文凌波,等.商用車驅動橋殼疲勞壽命的有限元仿真與實驗分析［J］.機械強度,2008,30（3）:503-507.