基于信號子空間的激光主動成像散斑去除

王燦進，孫 濤，王挺峰，郭 勁，劉玉龍

（1.中國科學院長春光學精密機械與物理研究所 激光與物質相互作用國家重點實驗室，長春130033；2.吉林省煙草專賣局 信息中心，長春130033）

0 引 言

激光主動成像［1］系統具有分辨率高、抗干擾能力強、不受環境光限制等優點，適用于微光、夜視以及遠距離暗目標的探測成像，目前已廣泛應用于遠距離監視、自動目標識別等領域［2－3］。在主動成像過程中，由于相干光經過目標表面反射或者通過無規則漲落的折射媒介傳播，會形成一種信號相關的乘性噪聲，即散斑噪聲，造成圖像質量嚴重下降。文獻［4］通過計算灰度概率分布曲線證明散斑噪聲是激光主動成像的主要噪聲，因此研究抑制散斑噪聲的算法是大多數激光主動成像系統都必須考慮的內容。

國內外學者提出諸多抑制散斑噪聲的經典算法，包括 均 值 濾 波［5］、Lee濾 波［6］、Frost濾 波［7］、Kuan濾波［8］及其改進算法［9］。這些濾波器使用一定大小的濾波窗口在圖像上滑動，使用不同算法計算出當前像素的替代值，其中Lee濾波由于在濾除噪聲和保留信號完整性之間能夠達到較好的平衡而倍受關注。這類窗口算法雖然在同類區域去除散斑噪聲效果較好，但運算時間較長，對于圖像邊緣和細節信息的保留能力也不理想。變換域降噪算法中使用較多的是小波軟閾值濾波［10－11］，這類算法缺陷在于閾值的選取較為困難，閾值過大容易丟失圖像細節信息，閾值過小則不能很好地去除噪聲。近年來出現了不少針對散斑噪聲的新算法，如Jarabo－Amores等［12］提出一種基于“mean－shift”濾波的去噪方法，該方法不必事先假設噪聲的統計模型而能夠達到與統計去噪相當的效果。Hyenkyun 等［13］提出基于交互技術（Shifting technology）的降噪方法，能夠快速有效地去除散斑噪聲。國內，文獻［14］使用SURE（Stein′s unbiased risk estimate）獲得近似最優的小波系數的權值，該方法優勢在于計算量很小。

信號子空間方法的基本思想是將原始信號通過K－L變換分解為信號子空間和噪聲子空間，通過濾除噪聲子空間噪聲分量的同時保留信號子空間的信號部分，能夠恢復出較為純凈的信號，該方法已經成功運用于語音和雷達信號降噪領域［15－16］。基于其優異的信噪分離效果，本文將該方法從一維推廣到二維空間，提出一種基于時域約束（TDC）的激光主動成像散斑降噪方法。將本文的TDC 降噪方法同經典的Lee、Frost和Kuan濾波作比較，結果表明本文算法具有出色的噪聲抑制效果，同時算法也具有很好的實時性。

1 散斑噪聲分析

被激光照射的目標表面相對于激光波長而言凹凸不平，相干光被不同位置反射后在像面處發生干涉，即形成散斑圖樣。散斑噪聲的數學模型如式（1）（2）所示：

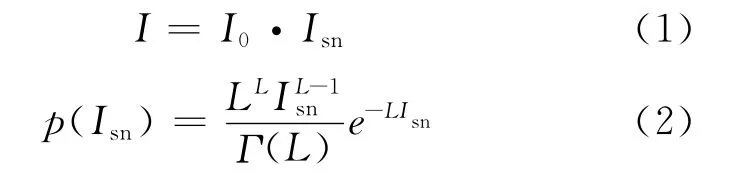
式中：I表示含噪圖像；I0表示無噪圖像；Isn表示散斑噪聲作用系數，服從均值為1，方差為1／L 的伽馬分布，L 是常數。

由式（1）可以看出散斑噪聲是一種乘性噪聲。為了將信號和噪聲分離，使用同態變換將其變為加性噪聲：

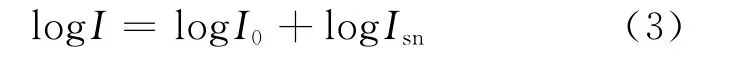
記上式為：

根據文獻［17］，同態變換后散斑噪聲的均值和方差的關系分別如式（5）（6）所示：

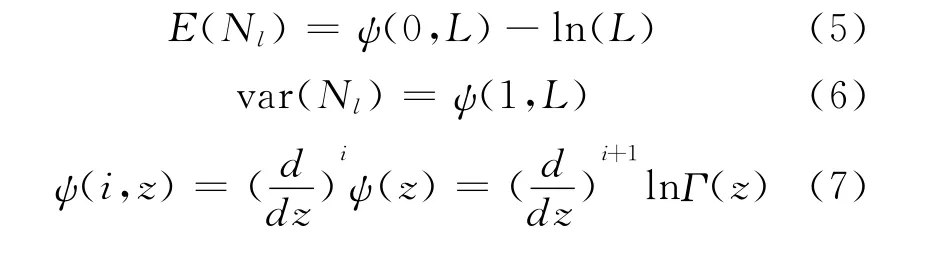
2 信號子空間濾波及TDC濾波方法

2.1 信號子空間

信號子空間技術是一種類似于傅里葉變換［18］、小波變換［19］的子空間變換技術。其原理是：帶噪信號的空間由信號子空間與噪聲子空間構成，噪聲能量均勻分布于整個空間中，而信號能量則只分布于信號子空間中。將帶噪信號分解至信號子空間和噪聲子空間，通過消去噪聲子空間的分量，就可以恢復出近似純凈的信號。該方法對于語音信號具有良好的去相關性，因而廣泛用于語音增強領域。本文接下來將這種方法推廣到二維圖像空間。

設無噪圖像的估計為：

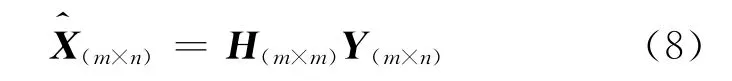
則誤差信號表示為：

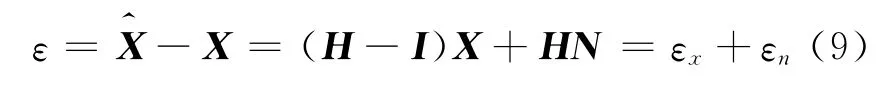
定義失真信號能量和殘余噪聲能量分別為：

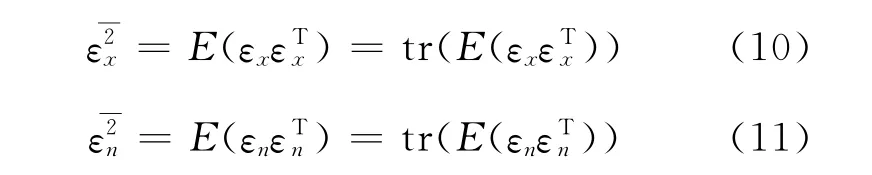
式中：tr（）表示取對角線上的元素。

為使失真信號能量達到最小，設置約束條件為：

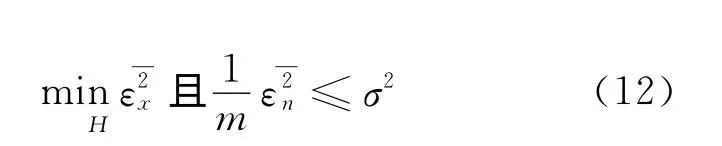
式中：σ2是常數。對上述約束最小值問題，可以采用Kuhn－Tucker條件得到Lagrange多項式：

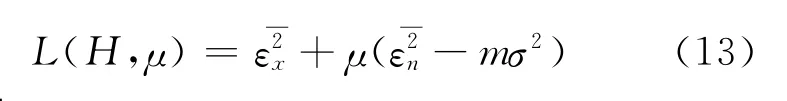
根據條件

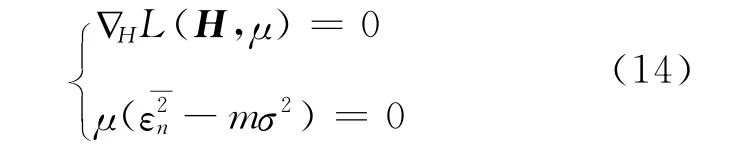
可以計算出濾波矩陣H 的估計值：

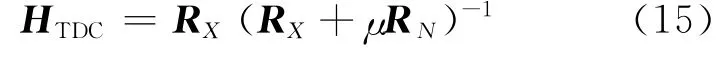
式中：RX＝E（XXT）是無噪圖像的協方差矩陣，RN＝E（NNT）是 噪 聲 的 協 方 差 矩 陣，μ 是Lagrange算子。將RX進行特征值分解，表示成信號子空間和噪聲子空間兩部分：

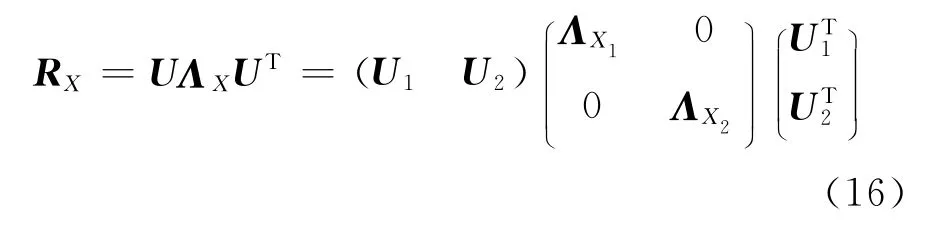
式中：U1、U2分別是m×r和m×（n－r）的特征值矩陣，r是信號子空間的維數，n－r是噪聲子空間的維數；ΛX1、ΛX2是特征值對角陣；代表的是RX在信號子空間的分量；代表的是RX在噪聲子空間的分量。

取RX的信號子空間的分量代入式（15），可得濾波估計矩陣：

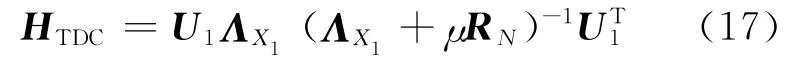
由式（16）（17）可知，為了得到HTDC，需要確定以下四個參數：信號子空間的維數r、無噪圖像的協方差矩陣RX、噪聲的協方差矩陣RN以及常數μ。

2.2 確定信號子空間維數r

估計信號子空間的維數，可以用奇異值分解實現。信號Y 的奇異值分解表示如下：

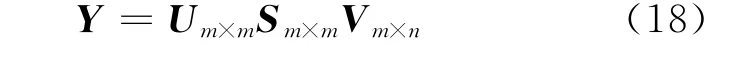
式中：S 是Y 的 奇 異 值 矩 陣，Sm×m＝diag（s1，s2，…，sm），s1≥s2≥…≥sm，即對角陣上的值采用降序排列。

信號某維度的奇異值大小代表該維度的重要程度，奇異值越大，對應該維度越重要。取S的前r個分量，則Y 可以近似表示為：

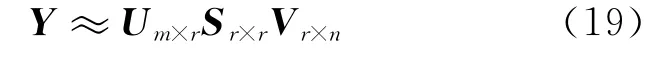
文中選取r的條件為：

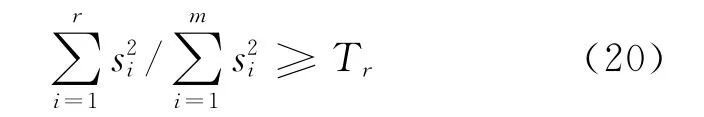
式中：Tr是一個接近于1的閾值，具體大小由實驗決定。

由于像素值為0的像素點經過log變換會出現無窮小，使Y 無法進行奇異值分解，因此同態變換前先將每個像素亮度增加10，待取指數恢復之后再減去10。

2.3 確定無噪圖像的協方差矩陣RX、噪聲的協方差矩陣RN

經過同態變換之后乘性噪聲變為加性噪聲，如式（4）所示，則可以得到

式中：RY＝E（YYT）可以直接由含噪圖像求得。對于RN，式（6）給出了它和常數L的關系，但是L難以估計。本文從小波分析的角度出發：在小波域上，圖像信號集中在低頻分量，而噪聲信號均勻分布在整個小波空間［16］，因此可以利用高頻子帶的小波系數估計噪聲的強度：

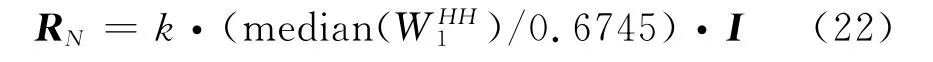
2.4 確定常數μ

μ 的取值會影響濾波后圖像的質量。μ 值大，可以較大程度地濾除散斑噪聲，卻會導致較嚴重的信號失真；μ 值小，能夠保留較多的細節信號，但會殘余更多的噪聲。選擇μ的值需要在信號完整性和濾波性能之間權衡。

根據文獻［16］，采用以下公式確定μ：式中：SNR 是圖像的信噪比；μ0 和s是常數，由實驗確定。

式（23）表示的是：對于高信噪比的圖像，噪聲較小，μ取較小的值，以保護信號完整性為主要目標；對于低信噪比的圖像，噪聲較大，μ 取較大的值，以濾波為主要目標。

2.5 基于信號子空間的TDC濾波方法

本文基于信號子空間的散斑去噪方法如下：

（1）對增加亮度后的圖像進行同態變換，將乘性噪聲變為加性噪聲。

（2）將圖像進行小波變換，并利用高頻分量估計噪聲方差RN。

（3）對Y 進行奇異值分解，估計信號子空間的維數r。

（4）計算無噪圖像的協方差矩陣RX＝RYRN，并根據式（16）對其進行特征值分解。

（5）根據式（17）計算變換矩陣HTDC，得到無噪圖像的估計值

（6）同態逆變換，得到最終的去噪圖像。

3 實驗驗證

實驗搭建一套基于距離選通技術的激光主動照明系統：使用532nm 波長、5mrad發散角的半導體泵浦固體脈沖激光器發射脈沖光束照射3.4 km 處的目標，用選通ICCD 接收反射信號，通過同步控制器控制選通快門的開閉。其中選通ICCD 由選通像增強器和CCD 組成，具有高增益、高靈敏度、成像清晰等優點。同步控制器控制ICCD 在納秒級的時間內進行選通，可以抑制雜散光，保證采集到較為清晰的含散斑圖像。圖1是實驗系統框圖，圖2是實驗系統實物圖。

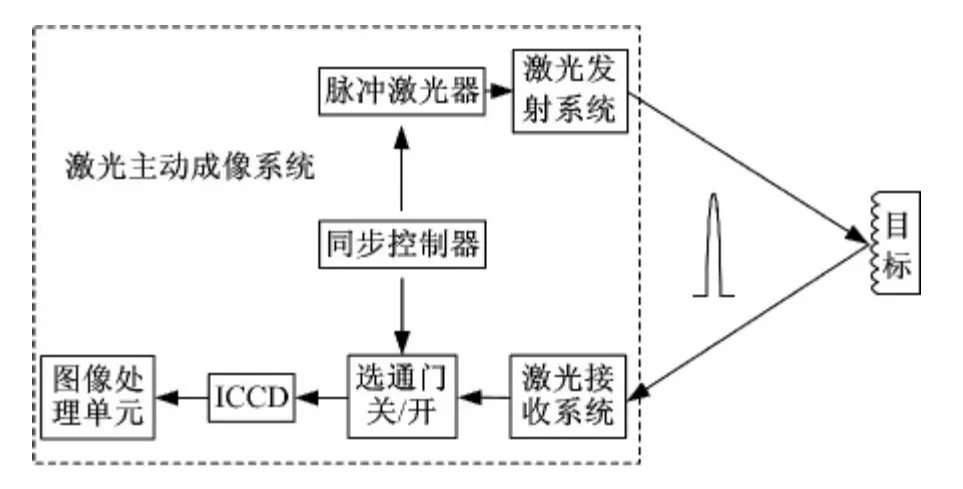
圖1 實驗系統框圖Fig.1 Block diagram of experimental system

圖2 實驗系統實物圖Fig.2 Photo of experimental system

截取ICCD 輸出圖像中被照亮的區域，最終得到的實驗圖像大小為150×150像素。分別采用Lee、Frost、Kuan和本文的TDC 濾波方法進行實驗，Lee、Frost和Kuan的濾波窗口均選為5×5。窗口大小選為5×5可以在濾除噪聲和保留圖像細節之間得到較好的平衡。實驗編程環境為：Windows XP、i7－2600 3.40 GHz CPU、2G內存、VS2008＋opencv軟件平臺。

圖3為4種算法的濾波效果對比，ICCD 的積分時間為50ns。

圖3 不同濾波方法的濾波結果Fig.3 Results of different denoising methods

從圖3直觀上看，Lee、Frost和Kuan結果圖中殘余較多的散斑噪聲，而TDC 濾波后的圖像最清晰，濾波效果最好。觀察圖像下方中間的門框，可以發現TDC 濾波后的邊緣更加清晰，這是因為其余3 種算法均使用鄰域像素進行加權操作，必將導致細節模糊。而TDC 算法將圖像矩陣當做整體進行運算，是對圖像信號的稀疏表示，信號子空間的信號部分沒有損失，故邊緣保持能力更強。

本文引入峰值信噪比PSNR［20］以評價濾波算法的有效性。改變ICCD 的積分時間，得到不同噪聲強度的圖像，分別用4種濾波方法進行實驗，計算其PSNR 值，比較濾波效果，結果如圖4所示。

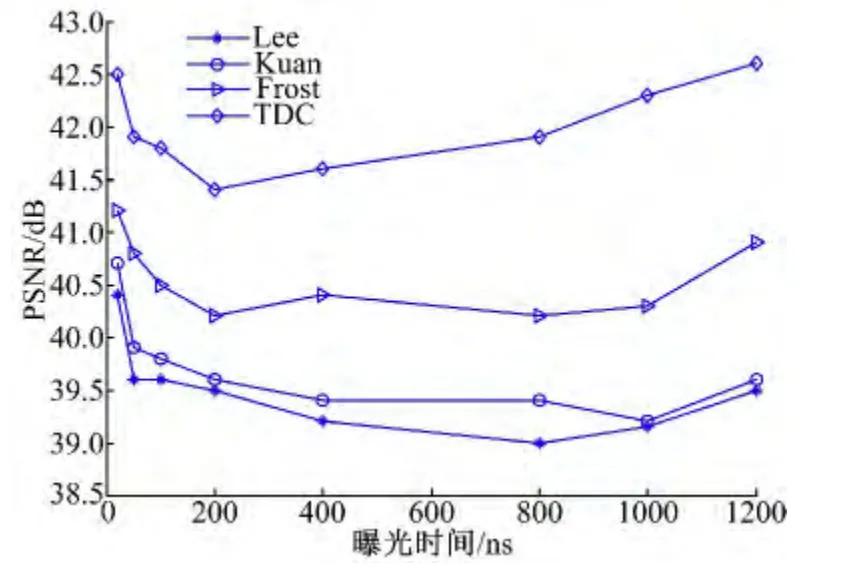
圖4 不同濾波算法的PSNR 曲線Fig.4 PSNR curves of different denoising methods

由圖4看出，本文TDC算法對于不同強度的噪聲能夠取得比經典的Lee、Frost和Kuan算法更好的濾除效果。觀察PSNR 曲線，隨著曝光時間的增加，TDC濾波算法的曲線與其余曲線的差值越來越大，這表示隨著噪聲的增大，TDC 的濾波性能優勢相對于其余算法越來越突出。這是因為對于Lee、Frost和Kuan 等窗口濾波而言，使用有限大小的濾波窗口信息，并不能很好地估計噪聲的方差，隨著噪聲的增加，濾波能力并不會顯著提升，濾波后殘余的噪聲會越來越大。而TDC算法的約束條件是將殘余噪聲限制在σ2范圍內，算法在整個圖像上進行噪聲強度的估計，并且只保留信號子空間中的非常小的噪聲能量，因此濾波效果更好。

表1統計的是不同算法對于150×150圖像的平均運算時間。可見本文算法比其余3種算法耗時要小得多。這是因為TDC 算法對整個圖像矩陣同時進行計算，而其余3種算法均需要滑動濾波窗口遍歷整個圖像區域。在本文的實驗條件下（成像區域大小為150×150，幀頻為25 幀／s），TDC濾波算法能夠滿足實時處理的要求。

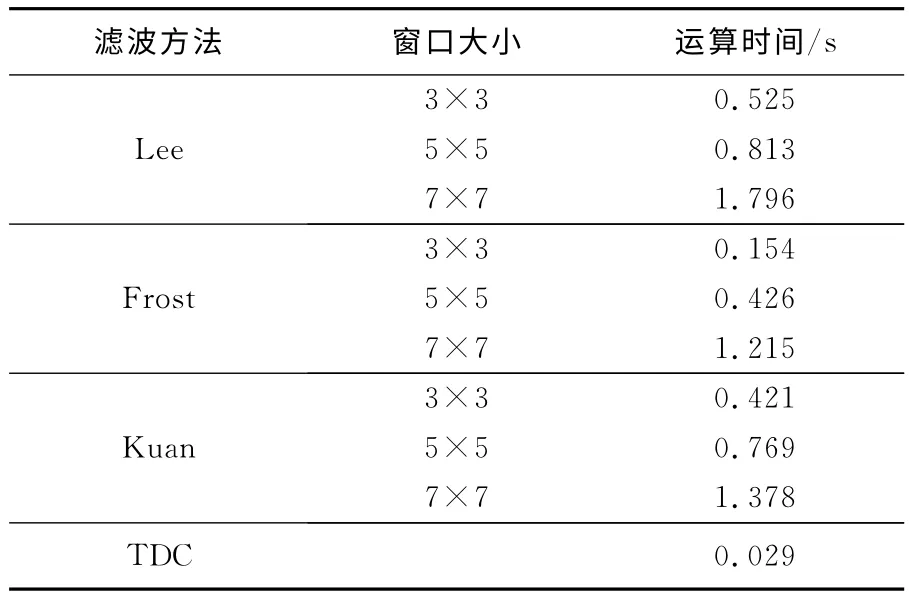
表1 不同算法的平均運算時間Table 1 Average running time of different denoising methods

4 結束語

受語音增強領域的子空間分解方法的啟發，本文在分析散斑噪聲數學模型的基礎上，提出一種基于信號子空間的激光主動成像去噪方法，并搭建了一套基于距離選通技術的激光主動照明系統進行實驗驗證。本文算法將含噪圖像分解為信號子空間和噪聲子空間，通過去除噪聲子空間并盡量保留信號子空間的能量，以取得良好的去噪效果。結果證明本文TDC 方法具有比經典的Lee、Frost和Kuan算法更好的去噪性能，同時縮短了計算時間，滿足激光主動成像系統實時性的要求。

［1］王燦進，孫濤，石寧寧，等.基于雙隱含層BP算法的激光主動成像識別系統［J］.光學精密工程，2014，22（6）：1639－1647.Wang Can－jin，Sun Tao，Shi Ning－ning，et al.Laser active imaging and recognition system based on double hidden layer BP algorithm［J］.Opt Precision Eng，2014，22（6）：1639－1647.

［2］錢方，孫濤，郭勁，等.無參考的特征點復雜度激光干擾圖像評估［J］.光學精密工程，2015，23（4）：1179－1186.Qian Fang，Sun Tao，Guo Jin，et al.No－reference laser－dazzling image quality assessment based on feature－point complexity［J］.Opt Precision Eng，2015，23（4）：1179－1186.

［3］趙建川，王弟男，陳長青，等.紅外激光主動成像和識別［J］.中國光學，2013，6（5）：795－802.Zhao Jian－chuan，Wang Di－nan，Chen Chang－qing，et al.Infrared laser active imaging and recognition technology［J］.Chinese Optics，2013，6（5）：795－802.

［4］李自勤，李琦，王騏.由統計特性分析激光主動成像系統圖像的噪聲性質［J］.中國激光，2004，31（9）：1081－1085.Li Zi－qin，Li Qi，Wang Qi.Noise characteristic in active laser imaging system by statistic analysis［J］.Chinese Journal of Lasers，2004，31（9）：1081－1085.

［5］Loupas T，McDicken W，Allan P.An adaptive weighted median filter for speckle suppression in medical ultrasonic images［J］.IEEE Trans Circuits System，1989，36（1）：129－135.

［6］Lee J S.Digital image enhancement and noise filtering by use of local statistics［J］.IEEE Trans Pattern Analysis and Machine Intell，1980，20：165－168.

［7］Frost V S，Stiles J A，Shanmugan K S，et al.A mode for radar images and its application to adaptive digital filtering of multiplicative noise［J］.IEEE Trans Pattern Analysis and Machine Intell，1982，4：157－165.

［8］Kuan D，Sawchuk A，Strand T，et al.Adaptive restoration of images with speckle［J］.IEEE Trans Acoust，Speech and Signal Process，1987，35（3）：373－383.

［9］Lu Y H，Tan S Y，Yeo T S，et al.Adaptive filtering algorithms for SAR speckle reduction［C］∥Geoscience and Remote Sensing Symposium，Lincoln，NE，USA，1996.

［10］Donoho D L.Denoising by soft－thresholding［J］.IEEE TransInform Theory，1995，41（3）：613－627.

［11］葉樹亮，張玉德，張煒.齒輪視覺檢測中的尺度與方向相關性聯合降噪［J］.光學精密工程，2014，22（6）：1622－1630.Ye Shu－liang，Zhang Yu－de，Zhang Wei.Scale and directional correlation combined denoiseing in gear visual inspection［J］.Opt Precision Eng，2014，22（6）：1622－1630.

［12］Jarabo－Amores P，Rosa－Zurera M，Mata－Moya D，et al.Mean－shift filtering to reduce speckle noise in SAR images［C］∥Instrumentation and Measurement Technology Conference，Singapore，2009.

［13］Hyenkyun W，Yun S.Alternating minimization algorithm for speckle reduction with a shifting technique［J］.Image Processing，2012，21（4）：1701－1714.

［14］李曉峰，徐軍，羅積軍，等.激光主動成像圖像噪聲分析與抑制［J］.紅外與激光工程，2011，40（2）：332－337.Li Xiao－feng，Xu Jun，Luo Ji－jun，et al.Noise analyzing and denoising of intensity image for laser active imaging system［J］.Infrared and Laser Engineering，2011，40（2）：332－337.

［15］Ikeda S，Ohtsuki T，Tsuji H.Signal－subspace－partition event filtering for eigenvector－based security system using radio waves［C］∥Personal，Indoor and Mobile Radio Communications，Tokyo，Japan，2009.

［16］Gu J，Yang J，Zhang H，et al.Speckle filtering in polarimetric SAR data based on the subspace decomposition［J］.Geoscience and Remote Sensing，2004，42（8）：1635－1641.

［17］Donoho D L，Johnstone I M.Ideal spatial adaptation by wavelet shrinkage［J］.Biometrika，1994，81（3）：425－455.

［18］鄧建青，劉晶紅.基于Fourier－Mellin變換和Keren算法的改進運動估計算法［J］.液晶與顯示，2011，26（3）：364－369.Deng Jian－qing，Liu Jing－hong.Improved motion estimation algorithm based on Fourier－Mellin transform and Keren algorithm［J］.Chinese Journal of Liquid Crystals and Displays，2011，26（3）：364－369.

［19］任志英，高誠輝，申丁，等.雙樹復小波穩健濾波在工程表面粗糙度評定中的應用［J］.光學精密工程，2014，22（7）：1820－1827.Ren Zhi－ying，Gao Cheng－hui，Shen Ding，et al.Application of DT－CWT robust filtering to evaluation of engineering surface roughness［J］.Opt Precision Eng，2014，22（7）：1820－1827.

［20］任文琦，王元全.基于梯度矢量卷積場的四階各向異性擴散及圖像去噪［J］.光學精密工程，2013，21（10）：2713－2719.Ren Wen－qi，Wang Yuan－quan.GVC－based fourthorder anisotropic diffusion for image denoising［J］.Opt Precision Eng，2013，21（10）：2713－2719.