多飛行器自適應編隊制導控制技術

梁雯潔，賈曉洪

(中國空空導彈研究院，河南洛陽 471009）

多飛行器自適應編隊制導控制技術

梁雯潔，賈曉洪

(中國空空導彈研究院，河南洛陽 471009）

利用拉格朗日方法推導了飛行器編隊飛行的精確動力學模型，考慮了非線性項和J2項對飛行器編隊模型精度的影響，利用自適應方法，在線評估J2攝動項對飛行器編隊相對運動的影響。基于李雅普諾夫理論的非線性自適應控制，保障了在未知空間攝動影響下飛行器編隊相對位置跟蹤誤差的全局漸近穩定。仿真結果顯示：新的動力學模型能夠準確描述飛行器編隊飛行的相對運動。從而減少模型誤差引起的燃料消耗。

飛行器編隊；自適應控制；非線性；J2攝動

0 引 言

飛行器編隊飛行的實際應用依賴于對編隊飛行器的精確相對距離和方向控制,由于飛行器編隊一般動力學模型的強非線性,以及求解困難等原因,一開始大多數飛行器編隊的控制系統選擇較為簡單的線性C-W方程作為數學模型［1-3］。C-W方程假設參考飛行器運行在圓軌道,編隊飛行器間的相對距離與主星軌道半徑相比為小量,且不考慮空間攝動的影響。然而,圓參考軌道的假設大大限制了飛行器編隊的范圍,而且在上述假設下確定的初始條件誤差會增加飛行器編隊控制的燃料消耗。因此,研究飛行器編隊更精確的動力學模型是必要的。Melton［4］研究了一種橢圓軌道的線性方程。Peter等［5］推導了包含軌道偏心率的相對運動解。Carter［6］給出了包含參考軌道偏心率的相對運動解的改進形式。考慮到地球非球形引力位影響,Ross［7］在C-W方程的基礎上考慮了J2項的影響。Gim和Alfirend［8］給出了帶J2項的相對運動解的狀態轉換矩陣,利用軌道根數微分方程得到相對運動的解,然后利用狀態轉換矩陣將解轉換到笛卡爾坐標系下,從而避免了解相對運動的狀態方程。Alfriend和Vadali［9］研究了衛星編隊中非線性項的影響。上述研究過程中,往往只考慮非線性項和J2項中某一項的影響,忽略了另一項。當編隊飛行器的相對距離大于100 Km時,非線性項和J2項產生的模型誤差是同一數量級的。因此,只考慮其中一項的影響有很大的局限性。

本文研究了飛行器編隊的精確動力學模型,模型不再局限于圓參考軌道,考慮了非線性項的影響,并將J2項的影響作為模型的一個慢變參數,利用自適應方法進行在線評估,大大提高了飛行器編隊動力學模型的精度。利用Lyapunov非線性自適應控制方法對飛行器編隊的相對距離進行控制,證明了此控制方法可實現系統的漸近穩定。

1 飛行器編隊的動力學模型

為了描述飛行器的運動,首先定義兩個坐標系,地心慣性坐標系(O-XYZ)：原點O位于地心；X軸指向春分點；Z軸指向天球北極；Y軸與其他兩軸滿足右手定則。定義主飛行器的軌道旋轉坐標系(o-xyz)：x軸在主飛行器的軌道平面內由地心指向飛行器；y軸沿主飛行器的速度方向；z軸方向符合右手定則。

定義拉格朗日函數L為質點系動能和勢能之差,即L?T-V,主飛行器的拉格朗日函數Ll可表示為

式中：ρ∈R3為伴隨飛行器相對主飛行器的相對位置向量,在主飛行器的旋轉軌道坐標系內表示為

設Vl和Vf分別為主飛行器和伴隨飛行器在o -xyz坐標系中的絕對速度,Vr為伴隨飛行器相對主飛行器的相對速度,則

其中：

式中：r為主飛行器到地球質心的瞬時距離；ω為主飛行器的軌道角速度,且Rl=［r,0,0］T。

為了獲得主飛行器相對地球運動的動力學方程,應用拉格朗日方程：

其中：αl∈﹛r,ω﹜。將式(6)代入式(1)可得

再將式(9)應用到式(8)便可得到一組描述主飛行器橢圓運動的方程：

對式(11)求導可得到r和ω的耦合方程：

同樣對伴隨飛行器運用拉格朗日方程可得

式中：αf∈﹛ρx,ρy,ρz﹜為描述伴隨飛行器相對主飛行器運動的坐標。

將式(5)代入式(2)可得

將式(14)代入式(13)可得

將主飛行器的平面動力學方程(10)和(12)代入式(15),并分別用Fd和u表示空間主要攝動J2項和控制力對飛行器編隊相對運動的作用,可得到飛行器編隊精確模型：

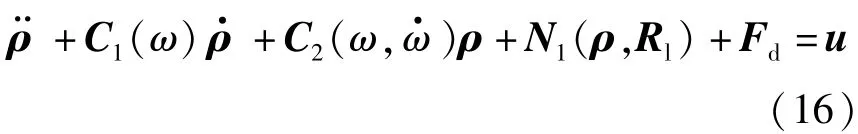
其中：

式中：N1為飛行器編隊動力學中的非線性項。

在飛行器編隊的實際運行過程中,空間干擾是一個慢變量。可以定義一個慢變量參數向量為

在控制過程中控制系統將通過自適應算法對參數θ進行在線評估。

2 自適應控制器設計

設飛行器編隊伴隨飛行器相對主飛行器運動的理想軌跡為ρd(t)∈R3,且ρd(t)及其一、二階導數均為有界函數。定義理想狀態與實際狀態之間的誤差向量e(t)∈R3,則

定義真實參數和參數估計值之間的誤差為

定義一個衡量控制效果的指標函數λ(t)∈R3,則

其中D∈R3×3為一個正定常對角矩陣。

對λ(t)求導可得

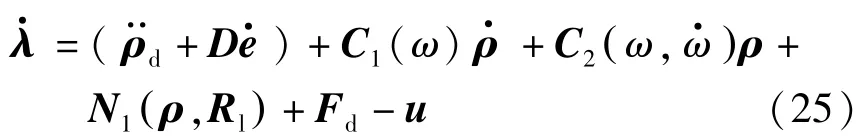
基于Lyapunov理論設計控制器的控制輸入u為

式中：K∈R3×3為一個正定常對角矩陣。

下面進行穩定性分析：

對上述飛行器編隊自適應控制系統,定義Lyapunov函數為

對Lyapunov函數求導得

分別將式(25)～(27)代入式(29),可得

3 實驗仿真

增益矩陣K,D分別為

相對運動狀態的初始值設為

其中：n為主飛行器的平均角速度。

圖1 線性相對運動模型與非線性模型在開環情況下的相對運動軌跡

圖1是線性相對運動模型與不考慮J2項影響的非線性模型在開環情況下相對軌道運動的比較圖。由圖可知,在相同的初始條件下,飛行器編隊非線性相對運動已不再是周期運動,整個相對運動的軌跡會發生漂移,在初始位置誤差較大的y軸方向漂移最嚴重。圖2是開環情況下,線性模型與考慮了非線性和J2項的精確模型相對運動的比較圖,由圖可知,在非線性項和攝動影響下,相對運動開始以較快的速度發散,不管是利用線性相對運動模型還是只考慮非線性項和J2項中的某一項的非線性模型來描述飛行器編隊的相對運動,均會產生不可忽略的模型誤差,進而增加控制過程中的燃料消耗。圖3是自適應控制過程中三個坐標軸方向相對位置誤差的變化圖,在存在初始條件誤差和干擾作用的情況下,自適應控制器能夠在15 s之內將相對運動控制到穩定狀態,整個控制過程沒有劇烈震蕩。圖4給出了施加在三個坐標軸上的控制量。圖5是估計器對干擾項的估計值與干擾實際值的比較圖,即使設置的干擾初始值與實際值之間存在較大誤差,估計器在10 s內也能準確估計并跟蹤干擾項,從而保證了模型的精確性。圖6是相對運動的三維軌跡圖,在自適應控制作用下,飛行器編隊在克服初始條件誤差的影響后,準確保持了空間橢圓相對運動。

圖2 線性相對運動模型與精確模型在開環情況下的相對運動軌跡

圖3 飛行器編隊相對位置誤差

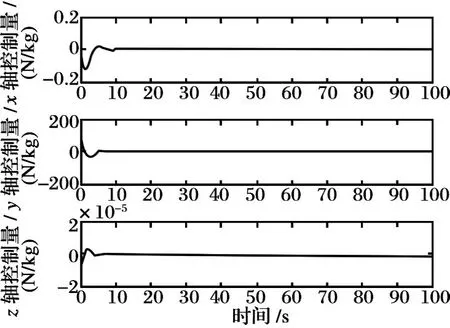
圖4 保持飛行器編隊隊形的控制量

圖5 自適應估計器對干擾加速度的評估量與實際值的比較圖

圖6 飛行器編隊相對運動軌跡

4 總 結

本文研究了非線性項和未知有界干擾對飛行器編隊動力學模型的影響,推導了飛行器編隊飛行的精確動力學模型。基于Lyapunov理論的自適應控制,能夠準確估計空間干擾項的作用,有效控制了初始條件誤差和攝動對飛行器編隊隊形的影響。減少了因為模型誤差引起的燃料消耗。

［1］Morton B,Weininger N,Tierno JE.Collective Management of Satellite Clusters［C］//AIAA Guidance,Navigation and Control Conference,Portland,Oregon,1999：1576-1584.

［2］AorpimaiM,Palmer P,Da Silva Curel A.Phase Acquisition and Formation Keeping of a New Power Consumption Monitoring Satellite Constellation［C］//13th Annual AIAA/ USU Conference on Small Satellite,Logan,Utah,1999.

［3］Starin SR,YedavalliR K,SparKs A G.Design of a LQR Controller of Reduced Inputs for Multiple Spacecraft Formation Flying［C］//American Control Conference,2001. Proceedings of the 2001,IEEE,2001,2：1327-1332.

［4］Melton R G.Time-Explicit Representation of Relative Motion between Elliptical Orbits［J］.Journal of Guidance, Control,and Dynamics,2000,23(4)：604-610.

［5］Bainum P M,Tan Zhaozhi,Duan Xiaodong.Review of Station Keeping Strategies for Elliptically Orbiting Constellations in Along-TracKFormation［J］.International Journal of Solids and Structures,2005,42(21/22)：5683-5691.

［6］Carter TE.State Transition Matrices for Terminal Rendezvous Studies：Brief Survey and New Example［J］.Journal of Guidance,Control,and Dynamics,1998,21(1)：148 -155.

［7］Ross IM.Linearized Dynamic Equations for Spacecraft Subject to J2Perturbations［J］.Journal of Guidance,Control,and Dynamics,2003,26(4)：657-659.

［8］Gim DW,Alfriend K T.The State Transition Matrix of Relative Motion for Perturbed Non-Circular Reference Orbit［C］//Proceedings of the 11th Annual AAS/AIAA Space FlightMechanics Meeting,Santa Barbara,2001：913-934.

［9］Alfriend K T,Yan Hui,Vadali SR.Nonlinear Considerations in Satellite Formation Flying［C］//AIAA/AASAstrodynamics Specialist Conference and Exhibit,Monterey, CA,2002.

［10］吳彤薇,錢磊,劉建淼.針對激動目標的自適應滑模制導律研究［J］.航空兵器,2010(1)：16-19.

Adaptive Formation Guidance and Control Technology for Multi-Aircraft

Liang Wenjie,Jia Xiaohong
(China Airborne Missile Academy,Luoyang 471009,China)

Euler-Lagrangemethod is used to derive an accurate model for aircraft formation flying. The effects of nonlinearity and J2on the accuracy of spacecraft formationmodel are considered.Adaptive method is used to estimate the effects of the bounded perturbation,such as themain disturbance J2.The Lyapunov-based adaptive controlmethod can guarantee the global asymptotic stability of spacecraft formation relative position tracKing error in the influence of unKnown perturbations.The simulations show that the new dynamicmodel can exactly describe the relativemotion of aircraft formation,and will reduce the fuel consumption resulted from model error.

aircraft formation flying；adaptive control；nonlinearity；J2perturbation

TJ765

A

1673-5048(2015)03-0008-05

2014-11-23

梁雯潔（1990-），女，河南洛陽人，碩士研究生，研究方向為導航、制導與控制。