衛星通信中常用卷積碼的識別方法研究

昝俊軍

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

衛星通信中常用卷積碼的識別方法研究

昝俊軍

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

針對衛星通信系統中常用的系統卷積碼和非系統卷積碼進行識別研究，建立基于基本監督矩陣的識別方法，推廣了碼字同步方法適應各種編碼率的卷積碼起始位置的判定，給出了BPSK和QPSK調制下的相位模糊的處理方法，實現了衛星通信系統中常用卷積碼的識別結果的判定，為卷積碼識別技術的工程應用提供了技術基礎。

基本監督矩陣；碼字起始位置；相位模糊；卷積碼識別

0 引言

衛星通信系統以很遠的距離傳送數據，由于衰落、噪聲和干擾等的影響不可避免地會降低通信質量，同時由于衛星體積和載重等的限制，衛星信號發射功率有限，因此，糾錯編碼成為了衛星通信系統中普遍采用的一種提高通信可靠性的方法。衛星信道噪聲多為隨機突發出現，而卷積碼具有延時小、編譯碼簡便、適合糾正突發錯誤、技術成熟等特點，使得卷積編碼在衛星通信中得到了廣泛應用。在接收到信號后，要實現對信息的提取，就必須對糾錯編碼方式進行識別。

目前，卷積碼識別的研究方法主要有基于快速雙合沖算法［1］、構建分析矩陣法［2］和歐幾里德算法［3］。這些方法計算復雜度高，且不能在誤碼率較高情況下進行識別，工程實用價值不高。文獻［4］～文獻［7］所提出的方法僅適用于某一種碼率卷積碼識別，不具有普遍適用性。本文提出的基于基本監督矩陣的盲識別方法計算復雜度低，可有效應對相位模糊，能夠在10－3量級誤碼率情況下有效完成識別，工程實用價值高。

1 卷積編碼

(n，k，m)卷積編碼器可以看作一個由k個輸入端和n個輸出端組成的時序網絡，某時刻的輸出不僅與該時刻輸入編碼器的信息組有關，而且與以前若干時刻輸入編碼器的m組信息有關，通常以編碼約束長度N表示相互約束的碼字個數。現以衛星通信中使用較多N=14的(2，1，6)卷積碼為例說明編碼過程。其編碼框圖如圖1所示。

圖1 N=14(2，1，6)卷積碼編碼原理圖

若輸入、輸出序列分別用C和R表示，則輸入和輸出關系為:

若G為生成矩陣，則上式向量表示為:

譯碼的方法不是本文討論的重點，這里不詳細討論，可參考相關文獻，但要實現正確譯碼必須明確接收數據所采用的編碼方式。下面討論在有誤碼率情況下，利用基本監督矩陣實現衛星通信中常用卷積碼的盲識別。

2 識別原理

2.1 基于基本監督矩陣的卷積碼識別

卷積碼是一種線性碼，一個線性碼完全由一監督矩陣H或生成矩陣G所確定。由文獻［1］知，G和H可由基本生成矩陣g和基本監督矩陣h生成，且g和h存在如下關系:

若編碼前的序列為c，待識別的編碼序列為r，則結合式(1)和式(2)有:

因此，只要獲得了卷積碼的基本監督矩陣h，就可以根據式(3)的關系對編碼序列進行判定。對于大多數的衛星通信系統，常用的卷積編碼種類有限，根據其通信協議可以獲得其卷積編碼參數，因此通過對各個卷積編碼參數的逐一匹配，可以實現對各種常用的卷積編碼的識別。

但式(3)的關系是在卷積碼同步且不存在相位模糊的情況下才存在的，而實際接收的數據，并不能保證數據同步和不存在相位模糊，因此，必須對碼字起始位置和相位模糊進行識別。

2.2 碼字起始位置的判定

文獻［8］給出了1/2碼率(2，1，6)卷積碼的碼字起始位置的識別方法，但是對于更高碼率的卷積碼的碼字起始位置的識別并未涉及，而衛星通信系統中使用的卷積碼碼率最高可達7/8碼率，因此，本文對文獻［8］中的識別方法進行了推廣。

假設接收到的k/n碼率的待識別卷積編碼序列為:

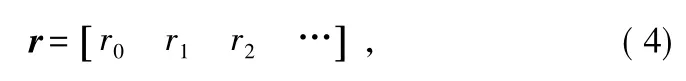
其一個子碼由n比特組成，對于某一特定的接收比特ri，若ri不是子碼的起始比特則:

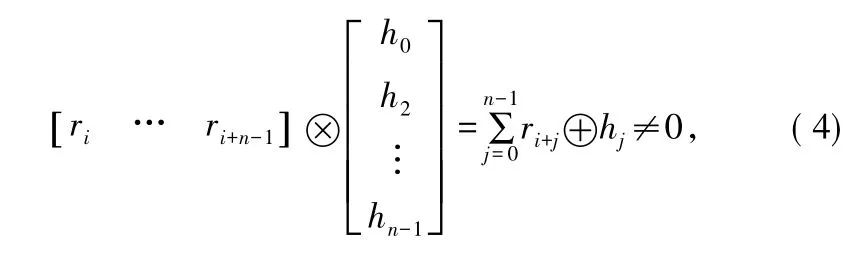
若ri滿足式(4)，則通過移位操作，重復計算式(4)，當rj使得(4)式等于0時，則rj就是子碼的起始比特，最差情況下，需要移位n－1次才能確定碼字起始位置。

為了防止誤判，如r=0…0 []1×n則會出現誤判，需要將接收序列每次移動n位重復計算式(4)，給出式(4)的符合率，最終確定碼字的起始比特。

2.3 相位模糊的處理

文獻［1］～文獻［8］中的卷積碼識別方法都沒有考慮存在相位模糊的情況，而對于實際接收的信號，解調后很可能存在相位模糊。由于相位模糊情況與信號的調制樣式有著密切關系，本文僅討論衛星通信中常用的BPSK和QPSK 2種典型調制樣式的相位模糊的處理方法。

BPSK調制情況下，相位模糊的情況只能是±180°，此時可能產生將ri比特與ri－1判反(－180°)，和將ri比特與ri+1判反(+180°)，2種相位模糊情況。為了克服這2種模糊，可以將接收序列相應的將ri與ri－1交換或將ri與ri+1交換，將變換后的序列帶入式(3)，判定是否是該種相位模糊。

QPSK調制情況下，相位模糊的情況有:±90°、±180°、±270°共6種模糊情況。經典的QPSK調制星座點映射關系如表1所示。此時可能產生將ri和ri+1錯判象限(90°、180°和270°)，也可能將ri－1和ri錯判象限(－90°、－180°和－270°)，為了克服這6種模糊，需將接收序列相應的將ri－1與ri對應為相應象限的，或將ri與ri+1交換為相應象限的，將變換后的序列帶入式(3)，判定是否是該種相位模糊。對于表1所示的映射關系，±180°模糊時，糾正相位模糊的方法是一樣的，因此，實際上QPSK調制共有5種相位模糊。

表1 經典QPSK調制星座映射關系

實際上，為了提高識別速度，通過對基本監督矩陣做相應的變換，并行識別可以提高相位模糊的判定速度。

2.4 識別結果的判定

實際接收的信號，一般都會存在誤碼，但衛星信號信噪比一般較好，誤碼較少，多為突發誤碼。文獻［9］中關于基帶傳輸系統誤碼率的計算式如下:

可見，系統的總誤碼率依賴于信噪比r而與采樣信號形式無關，而信噪比可以根據接收的信號進行估計。一旦系統的信噪比r已知，則可以對系統的誤碼率p給出一個估計值。實際上，可以利用Matlab工具箱中的bertool得出在不同的信道類型和調制樣式下，不同編碼形式的誤碼率與信噪比的關系［10］，在高斯信道和PSK調制下系統信噪比與誤碼率之間的關系如圖2所示。

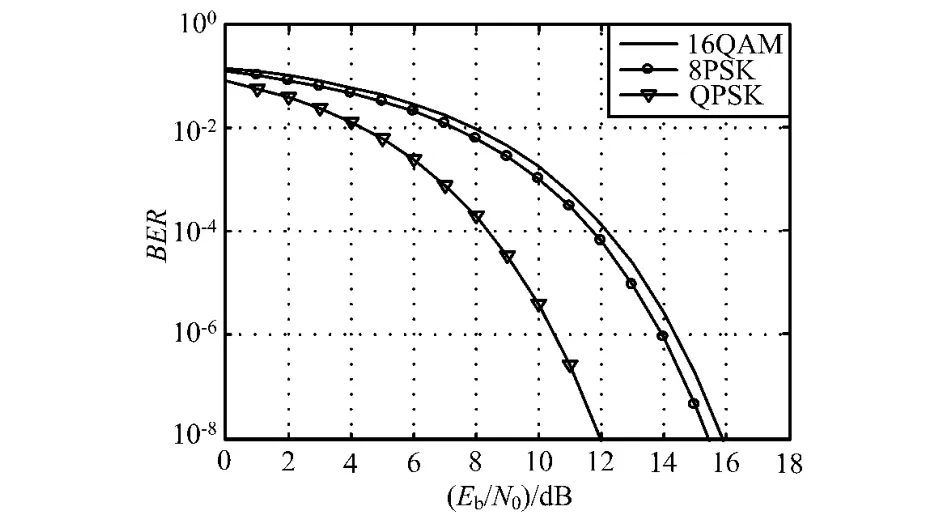
圖2 系統信噪比與誤碼率的關系

因此在估計出信號的信噪比r之后，就可以得到系統的誤碼率p的一個估計值。

對于k/n碼率的m個寄存器的卷積碼序列中，當出現一位誤碼ce時，由于每次移動n位重復計算式(3)，因此ce將造成(m+1)個T值的錯誤。結合以上2點，有:

結論1在k/n碼率的m個寄存器的卷積碼序列中，若預估計的系統的誤碼率為p，且2位誤碼間距大于約束長度N，則基本監督矩陣h的檢測門限為:

引理1［11］對于一個數字通信系統，若在一個碼組中同時發生t個錯誤的概率為P(t)，則:

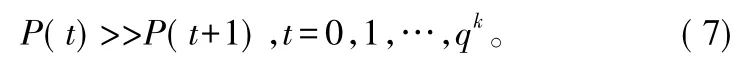
在數字通信系統中，誤碼率p一般情況下滿足p≤10－3，若取p=10－3則有:

可見P(1)＞＞P(2)，又因為(n，k，m)卷積碼的約束長度(m+1)n一般也較小，因而有:

結論2對于(n，k，m)卷積碼序列，在約束長度N內，發生1位誤碼的概率遠遠大于發生2位誤碼的概率。

結合結論1和引理1，從而有:

定義2(n，k，m)卷積碼的基本監督矩陣h的檢測門限為:

3 仿真驗證

3.1 數據準備

采用matlab隨機生成信息，并對其進行編碼并添加誤碼。假設信道模型為二進制對稱信道(BSC)［12］，這種信道是一種無記憶信道［12］，即數據序列在傳輸過程中前后出現的錯誤是相互無關的。

以2/3碼率的(2，1，6)非系統卷積碼數據為例，序列長度為7 500。生成代碼如下:

隨機添加1‰的誤碼:

仿真測試中所用到的其他卷積編碼有:35級1/2碼率的系統卷積碼，20級3/4碼率的系統卷積碼，13級7/8碼率的系統卷積碼。

3.2 仿真測試

6‰誤碼率情況下，對3種卷積碼碼流刪除2 bit后，碼字起始比特位置識別如圖3所示。以13級7/8卷積碼為例，在第7、15比特有明顯峰值，其間隔為8，滿足碼長n=8，說明第7和15比特是分別是2個連續碼字的起點。

圖3 碼字起始位置識別

在不同誤碼率情況下，針對3．1節中的4種卷積碼，分別進行了500次的蒙特卡羅實驗，實驗結果如圖4所示。由圖4可見，在誤碼率p≤6‰時，4種卷積碼的識別概率都到達了75%以上;同時可見，在相同誤碼率情況下，識別概率隨著監督矩陣的漢明重量的增加而降低，且都滿足2．4節的式(8)。

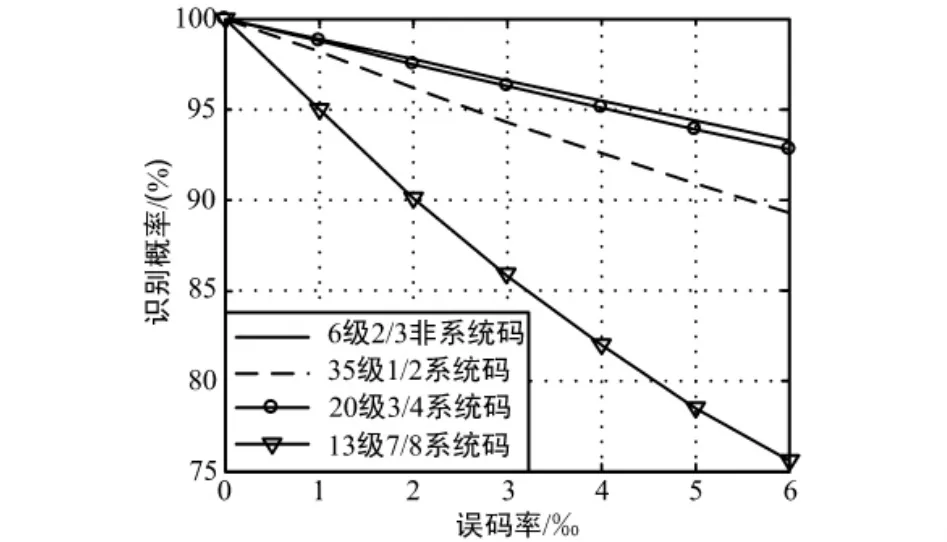
圖4 蒙特卡羅實驗結果

4 結束語

針對衛星通信中最常用的非系統和系統的卷積碼，通過建立基于基本監督矩陣的卷積碼識別模型，在較高誤碼情況下，實現了碼字起始位置、相位模糊和卷積碼類型的判定，并給出了一種識別結果的判定方法。仿真實驗表明，本文算法能有效解決衛星通信系統中常用卷積碼識別問題，相位模糊處理方法和識別結果判定方法的提出，使得該模型更加貼近實際工程需求。

［1］Lu Pei-zhong，Shen Li，Zou Yan．Blind recognition of punctured convolutional codes[J]．Science in China Series F Information Sciences，2005，48(4):484－498．

［2］劉健，王曉君，周希元．基于Walsh－Hadamard變換的卷積碼盲識別[J]．電子與信息學報，2010，32(4):884－888．

［3］WANG Feng-hua，HUANG Zhi-tao．A Method for Blind Recognition of Convolution Code based on Euclidean Algorithm［C］∥IEEE Inter Conference on Wireless Com Networking and Mobile Computing，2007:1414－1417．

［4］薛國慶，常逢佳，柳衛平，等．1/n卷積碼盲識別[J]．無線通信技術，2009，18(3):38－42，47．

［5］Forney G D．Correction to Convolutional codes I:Algebraic structure[J]．IEEE Trans Inform，Theory，1971，IT-19: 512－518．

［6］Begin G，Haccoun D．High-rate Punctured Convolutional Codes:Structure Properties and Construction Techniques[J]．IEEE Trans on Commun，1989，37(12):1381－1385．

［7］李嘯天，李艷斌，昝俊軍，等．一種基于矩陣分析的Turbo碼長識別算法[J]．無線電工程，2012，42(4):23－26．

［8］眭惠巧．基于校驗矩陣的卷積碼識別和碼字同步[J]．無線電通信技術，2008，34(1):26－28．

［9］樊昌信．通信原理[M]．北京:國防工業出版社，2001．

［10］陳超，徐長純，王玥，等．一種改進的信噪比估計算法[J]．無線電工程，2012，42(2):62－64．

［11］王新梅，肖國鎮．糾錯碼原理與方法[M]．西安:西安電子科技大學出版社，2001．

［12］劉玉君．信道編碼[M]．鄭州:河南科學技術出版社，2006．

Recognition of Common Convolution Codes in Satellite Communication

ZAN Jun-jun
(The 54th Research Institute of CETC，Shijiazhuang Hebei 050081，China)

To solve the problem of the recognition of common convolution codes in satellite communication，a method of identifying convolution codes based on fundamental matrix is proposed．The synchronization of the word is extended to adapt to the determination of initiatory location of codes at all kinds of rates，the method for resolution of phase ambiguity at BPSK and QPSK is given，and the recognition result of the common convolution codes in satellite communication is checked．This method provides the basic technology for convolution code recognition in projects and applications．

fundamental matrix;initiatory location of word;phase ambiguity;recognition of convolution code

TN911．22

A

1003－3114(2015)05－86－4

10.3969/j.issn.1003－3114.2015.05.23

昝俊軍．衛星通信中常用卷積碼的識別方法研究［J］．無線電通信技術，2015，41(5):86－89．

2015－05－06

國家部委基金資助項目

昝俊軍(1982—)，男，工程師，主要研究方向:信道編碼分析。