矩形巷道圍巖散熱規律數值模擬研究

劉彥青，宇 星

(中國礦業大學(北京) 資源與安全工程學院， 北京 100083)

矩形巷道圍巖散熱規律數值模擬研究

劉彥青1，宇 星1

(中國礦業大學(北京) 資源與安全工程學院， 北京 100083)

針對矩形巷道圍巖散熱規律，建立二維巷道圍巖散熱模型，采用有限體積法對巷道圍巖溫度場進行解算，計算模型中考慮了構成巷道圍巖的不同巖層的物性差異。利用計算數據擬合曲線方程方法得到巷道圍巖散熱速率公式，該式可適用于煤巷與巖巷，最后推導得出整段巷道圍巖散熱速率公式,包括掘進巷道與使用中巷道，對制定井下熱害防治措施具有一定的指導意義。

數值模擬；圍巖溫度場；物性差異；圍巖散熱速率

0 引 言

前人在圍巖溫度場數值模擬研究過程中將圍巖視為具有各向同性單一的均質介質[1-6]，數學模型比較理想化，沒有考慮到地層中不同巖層之間的物理性質差別，致使圍巖溫度場解算結果偏離實際圍巖溫度場。其中煤體與巖體的物理性質差別較大，包括密度、比熱、導熱系數等，煤巷圍巖散熱與巖巷圍巖散熱存在一定差別。本文考慮了巖體與煤體的物理性質差異，以及沿層面方向與垂直于層面方向的導熱系數差別，深入分析研究了煤巷與巖巷的圍巖散熱規律。

1 巷道圍巖散熱模型的建立

1.1 物理模型的建立

模型一為巖巷，作為參照模型，模型中煤層的頂底板巖層性質相同，重點分析煤層對于煤巷圍巖散熱的影響，針對3種煤巷形式分別建立了3個物理模型，模型二為半巖巷煤巷，煤層為薄煤層，模型三為全煤厚掘進煤巷，煤層為中厚煤層，模型四為沿煤層底板巷道，煤層為厚煤層。

模型中煤巷形狀為矩形，實際情況中煤巷形狀大多為梯形，前人研究[7,8]表明圍巖溫度場受巷道形狀的影響范圍僅限于靠近巷壁的很小一段距離，相對于整體圍巖溫度場而言，巷道形狀的影響可忽略。

1.2 數學模型的建立

1.2.1 假設條件

(1) 煤層為單一均質的介質，沿層面方向導熱系數大于垂直于層面方向導熱系數，忽略煤層瓦斯運移的影響，不考慮煤層氧化放熱影響；

(2) 頂底板為單一均質的介質，沿層面導熱系數大于垂直于層面的導熱系數；

(3) 未考慮巷道壁面水分蒸發影響。

1.2.2 控制方程及解算條件

圍巖散熱問題是二維導熱問題，考慮了煤層與頂底板巖層為層狀介質，其沿層面方向導熱系數與垂直于層面方向導熱系數差別較大，式(1)為二維的導熱微分方程。

(1)

邊界條件：計算區域邊界處熱流密度為0，即第二類邊界條件(絕熱邊界條件)，見式(2)，巷壁處為第三類邊界條件，見式(3)。

(2)

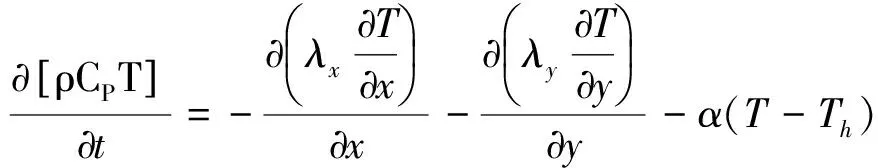
(3)

初始條件：巷道剛掘開時圍巖各處溫度均為原始巖溫。

式中,T為溫度，k;t為時間，s;λ為導熱系數，W/(m·k)，ρ為圍巖密度，kg/m3;Cp為圍巖的比熱容，J/(kg·k);α為對流換熱系數，W/(m2·k);Th為巷道風流溫度，k;

2 數值解算及結果分析

2.1 網格劃分

巷道圍巖散熱物理模型具有對稱型，計算區域采用結構式網格劃分方式，易于實現非均質巷道圍巖參數賦值,見圖1。

圖1 網格劃分示意圖

2.2 控制方程離散

根據計算區域網格劃分形式，對導熱方程采用基于有限體積法的C-N格式進行離散，每個節點離散方程中均包含10個溫度值，即當前時刻與該節點相鄰的四個溫度值、前一時刻該節點溫度值、前一時刻與該節點相鄰的四個節點的溫度值，其中當前時刻溫度值為未知量，上一時刻溫度值為已知量。通過求解方程組計算得到當前時刻計算區域內溫度場。

該算法可以保證在計算過程中時刻滿足質量守恒定律，解算結果具有物理真實性。

2.3 解算程序編制

利用vb語言編制了解算程序，程序結構流程見圖2。

圖2 程序流程圖

2.4 解算結果

2.4.1 計算參數選取

數值模擬計算中基本參數設置見表1。

2.4.2 巷道圍巖溫度場分布

圖3、圖4為巷道圍巖溫度場解算結果圖，模型一中圍巖溫度降低區域明顯大于后三種模型，且模型四中圍巖溫度降低區域最小，說明煤層存在影響了巷道圍巖溫度場分布。

表1 數值模擬基本參數

圖3 巷道暴露28 d后四種模型圍巖溫度場

圖4 巷道暴露169 d后四種模型圍巖溫度場

2.4.3 掘進巷道圍巖散熱速率

圖5為巷道巷壁散熱速率-時間的對數圖，從圖中可看出厚煤層煤巷與巖巷的巷壁散熱速率差別最大，即煤層愈厚，巷壁圍巖散熱愈小。

采用解算數據擬合方法可得到巷道圍巖散熱速率公式，擬合公式見式(4)，擬合系數見表2，式中a值、b值與巷道圍巖條件(巖層導熱系數、巖層厚度、巖層密度等)、巷道條件(巷道的形狀、尺寸、風流大小等)密切相關：

由表中R2可知該式對各種條件下巷壁圍巖散熱速率曲線的擬合程度高，該式可用于描述巷道圍巖散熱速率。

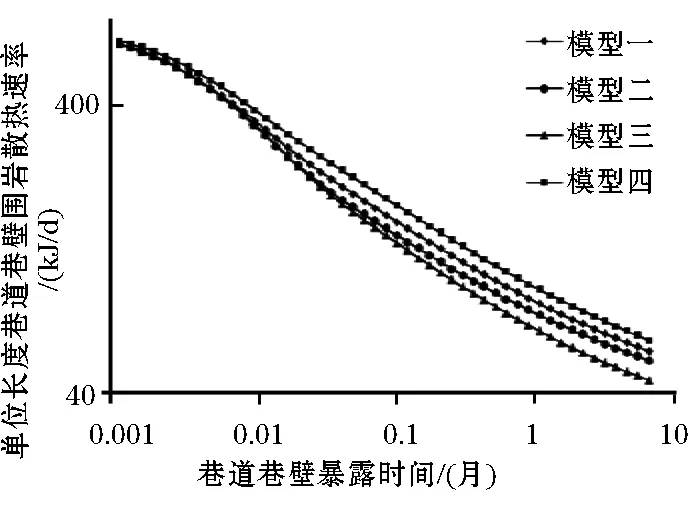
圖5 巷道巷壁圍巖散熱速率(對數圖)

(4)

表2 擬合式系數表

2.5 整段巷道圍巖散熱速率

2.5.1 掘進中巷道圍巖散熱速率

掘進巷道的已掘巷道巷壁圍巖散熱速率隨著暴露時間增大而衰減。掘進巷道巷壁圍巖散熱速率可通過對各段巷道巷壁圍巖散熱速率進行積分求得，見式(5)。

(5)

式中，l為已掘巷道長度，m；v為巷道掘進速度,m/d。

2.5.2 使用中巷道圍巖散熱速率

已使用巷道的暴露時間為巷道掘進時間和巷道使用時間之和，其巷壁圍巖散熱速率較掘進巷道小，式(6)為t時刻整段巷道圍巖散熱速率。

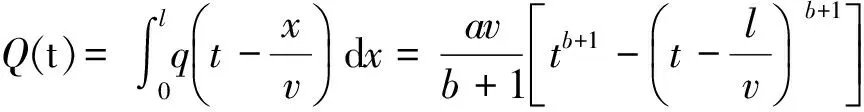
(6)

式中，t為該巷道掘進時間與使用時間之和，單位為月；

2.5.3 整段巷道圍巖散熱速率公式參數求解

整段巷道圍巖散熱速率公式確定的關健之處在于如何得到a值、b值，而其他參數如掘進速度、巷道長度等為已知量。

上文已驗證了不同條件下巷道圍巖散熱速率公式均可由式(4)表示，因此可根據式(4)，將數值模擬解算結果中任意兩個不同時刻下的巷道圍巖散熱速率分別代入式(4)中聯立可求解得一組a值與b值。

為了得到比較精確的a值與b值，可以選取多組巷道圍巖散熱速率結果求解得到多組a值與b值，然后分別對a值與b值求平均值。

在上述研究基礎上，編制了巷道圍巖散熱速率解算軟件，該軟件主要包括圍巖溫度場求解模塊與整段巷道圍巖散熱速率公式參數求解模塊。

3 結 論

(1) 建立了非均質的、各向異性的、非穩態的二維巷道圍巖散熱模型，利用VB程序語言編制了計算軟件，進行了數值解算，解算結果顯示了煤巷與巖巷圍巖散熱具有明顯差異性，說明將巷道圍巖視為單一的均質的介質會造成一定程度偏差，研究巷道圍巖散熱必須考慮圍巖的物性差異。

(2) 采用數據擬合曲線方式得到了巷道圍巖散熱速率公式，該公式對煤巷與巖巷圍巖散熱計算結果擬合程度極高，具有普遍適用性。

(3) 根據巷道圍巖散熱速率公式推導出整段巷道圍巖散熱速率公式、已使用巷道巷壁圍巖散熱速率公式，并給出如何確定公式參數的方法，編制了巷道圍巖散熱速率解算軟件，具有現場實用性。

[1]樊小利，張學博.圍巖溫度場及調熱圈半徑的半顯式差分法解算[J].煤炭工程,2011(7):82-84.

[2]秦躍平，王 健，郝永江等.基于有限體積法的巷道圍巖散熱無因次分析[J].礦冶工程，2013,33(3)：5-7.

[3]胡增輝,李曉昭,趙曉豹，等.隧道圍巖溫度場分布的數值分析及預測[J].地下空間與工程學報,2009,5(5):867-872.

[4]秦躍平，秦鳳華，于明學．用有限單元法研究回采工作面圍巖散熱[J].遼寧工程技術大學學報(自然科學版)，1999,18(4):342-346．

[5]周西華，單亞飛，王繼仁.井巷圍巖與風流的不穩定換熱[J].遼寧工程技術大學學報(自然科學版),2002,21(3):264-266.

[6]牛平安.利用 Fluent軟件模擬躍進煤礦巷道風溫變化規律[J].煤炭與化工，2013，36(4)：10-12.

[7]張習軍, 姬建虎, 陸 偉.深熱礦井巷道圍巖的熱分析[J].煤礦開采,2009,14(2):5-7.

[8]侯棋棕,沈伯雄.調熱圈半徑及其溫度場的數值解算模型[J].湘潭礦業學院學報,1997,12(1):9-16.

2014-07-23)

劉彥青 (1989-)，男，山西忻州人，碩士研究生，Email：lyqing0906@163.com。