基于HALLEN方程法的半波天線的參數計算*
徐曾春,盧洲(南京工業大學電子與信息工程學院,江蘇南京211816)
基于HALLEN方程法的半波天線的參數計算*
徐曾春,盧洲
(南京工業大學電子與信息工程學院,江蘇南京211816)
在現代電磁工程中,對于邊界不復雜的問題,可用解析法得到精準解,但較復雜的邊值問題用解析法不能得到解答,需要數值法。在此導出HALLEN方程法,用MATLAB軟件實現,它能夠非常接近解析值,說明其正確性。矩量法是求解電磁場邊界值問題中一種行之有效的數值方法,利用矩量法將HALLEN法的積分方程化為差分方程,將積分方程中積分化為有限求和,從而建立代數方程組,用MATLAB編程進行數值計算和仿真。最后得出結論,矩量法分析能夠接近其解析解,說明其正確性。
矩量法;HALLEN方法;半波天線;MATLAB
0 引言
自赫茲和馬可尼發明了天線以來,天線在社會生活中的重要性與日俱增,如今已成不可或缺之勢。天線是人們見聞世界的耳目,是人類與太空聯系的紐帶,是文明社會的組成要素[1]。
矩量法是求解電磁場邊界值問題中一種行之有效的數值方法,其數學本質是一種求解線性方程的方法[2]。矩量法[3-4]所做的工作是將積分方程化為差分方程,或將積分方程中的積分化為有限求和,從而建立代數方程組,故它的主要工作是用計算機求解代數方程組,因而在電磁場數值計算方面得到了廣泛的應用,并已得到了國內外學者的公認。HALLEN E在1938年提出積分方程法[5-6],首先從假定的電流分布用矢量磁位寫出天線表面外部的電場公式,然后令此電場等于天線表面內部因克服集膚效應引起的阻抗所需要的電場強度,由此求得表示電流分布的積分方程式。國內外對半波天線的研究主要集中于激勵原理、特性、實驗等方面的討論,而關于天線方向圖和電流分布等參數計算和分析很少。張黎明[7]、姜光興[8]等人利用矩量法對半波天線的參數進行了計算。HAFIANE A等人[9]利用天線陣模型對天線的參數進行了計算。基于以上的研究,本文利用HALLEN方法計算并仿真出半波天線的電流分布、功率增益和方向圖,計算過程中不但簡化了數值分析的復雜性,而且減小了計算量并提高了其精度。
1 天線的關鍵參數推導
1.1 矩量法的數學表述[7,10]設一個非其次方程為:

其中,L為微分算子或積分算子,f為待求的場量或響應,g為已知的源或激勵。
設空間為線性的,在算子L的定義域內選擇一組函數{fn},將待求函數f展開為它們的組合:

其中,an為待求系數,fn稱為基函數或展開函數,由自己選定。將式(2)代入式(1),并因L為線性算子,可得:

在L域內選擇一組加權系數(或稱檢驗函數)W1、W2、L、Wn的集合{Wm},并對每個Wm取式(3)的內積,可得:

式(4)可寫成如下的矩陣形式:

其中
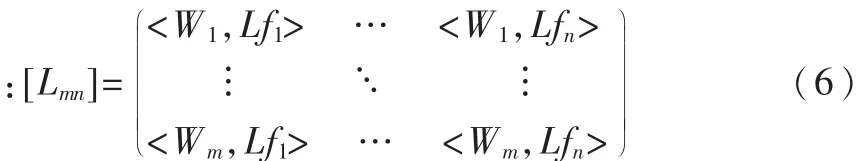
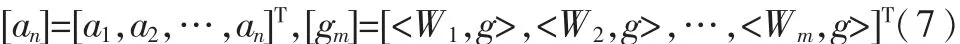
如果[Lmn]有逆矩陣存在,記為[Lmn]-1,則待求系數an可由下式解得:

于是可將f寫成f=[fn][am]=[fn][Lmn]-1[gm]。
1.2 方向圖
將方向性函數以曲線方式描繪出來,稱之為方向圖。它是描述天線輻射場在空間相對分布隨方向(q,f)變化的圖形,通常指歸一化方向圖。
(1)立體方向圖
變化q和f得到的方向圖為立體方向圖,它綜合描述了天線在各個方向上的輻射情況。
(2)E面、H面方向圖
E面是包含最大輻射方向的電場矢量所在的平面。用E面去截取立體方向圖,則得到E面方向圖。
H面是包含最大輻射方向的磁場矢量所在的平面。用H面去截取立體方向圖,則得到H面方向圖。
1.3 半波對稱天線
由于半波天線是特殊的對稱天線,因此在這里先介紹對稱天線的概念,導出對稱天線的參數。
對稱天線由兩臂長各為l、半徑為a的直導線或金屬管構成,如圖1所示,它的兩個內端點為饋電點。對稱天線是一種應用廣泛的基本線形天線,它既可單獨使用,也可作為天線陣的組成單元。

圖1 對稱天線的輻射場計算
對稱天線上的電流分布為:
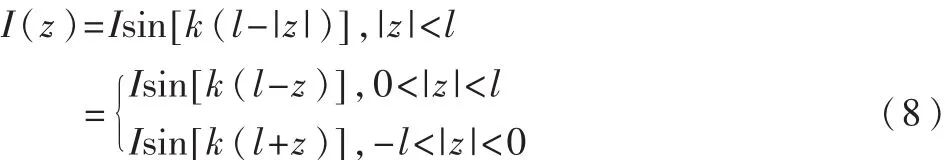
故對稱天線的輻射場為:
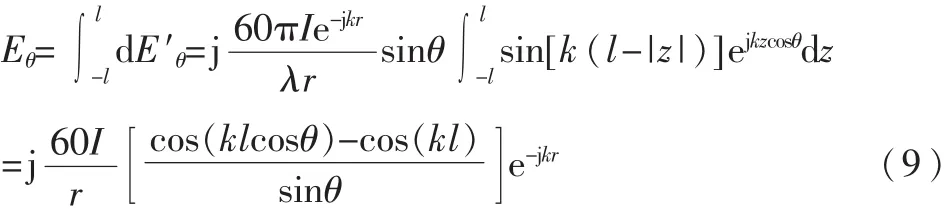
可見,對稱天線的歸一化方向性函數為:
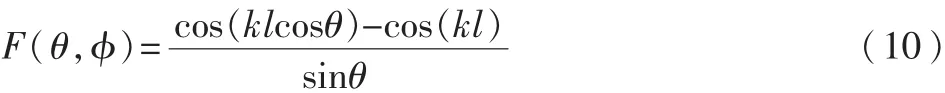
1.4 功率增益
天線增益用來衡量天線對某一特定方向的收發信號的能力,定量地描述某一天線將輸入功率集中輻射的程度[11]。在相同距離和相同輸入功率的條件下,天線在最大輻射方向上的輻射功率密度Wmax和理想無方向性天線的輻射功率密度之比以G表示,即:
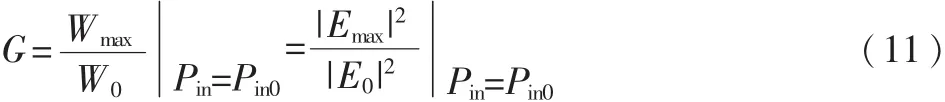
其中,Pin是實際天線輸入功率,Pin0是理想無方向性天線的輸入功率。
對于有耗情況:Wr=hAWmax,Pr=hAPin。
此時增益表達式可以寫成:
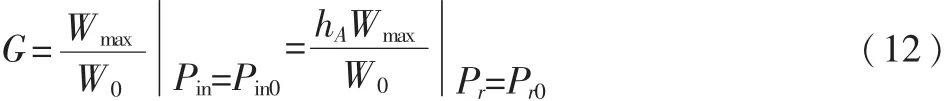
得到天線增益與方向系數的關系為:

天線的有效輻射功率可以表示為:

1.5 電流分布
從前面的介紹可知,HALLEN法從積分方程求解天線的電流分布,知道了電流分布和加在輸入端上的電壓。
2 仿真結果與分析
前面用HALLEN方法計算出了半波天線的電流分布、功率增益和方向圖參數的表達式,最后用MATLAB編程進行數值計算和可視化[12]。
2.1 電流分布
用MATLAB仿真,結果如圖2所示。
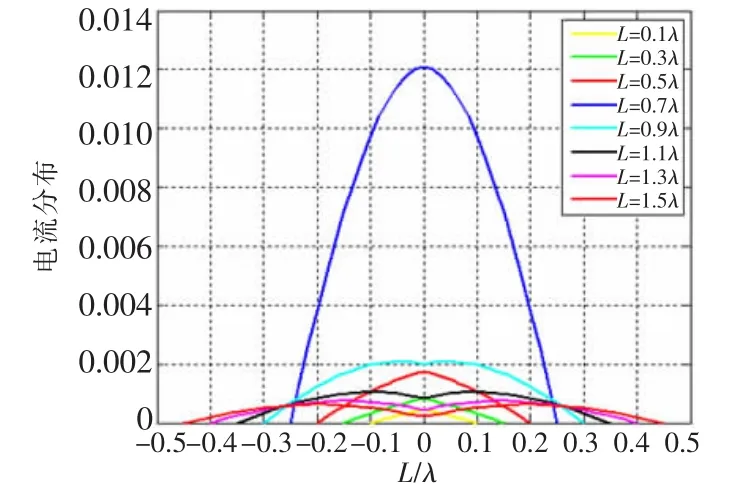
圖2 不同L/l電流分布圖
由圖2可知,半波振子天線L/l=0.5的電流分布最大,饋點電流最大,輻射電阻近似等于輸入電阻,因為半波振子的輸入電流正好是波腹電流。
2.2 方向圖
將方向性函數以曲線方式描繪出來,稱之為方向圖。它是描述天線輻射場在空間相對分布隨方向(q,f)變化的圖形[8,13]。
E面方向圖(二維)如圖3所示。

圖3 不同L/l的E面方向圖
H面方向圖(二維)如圖4所示,歸一化的H面方向圖如圖5所示。
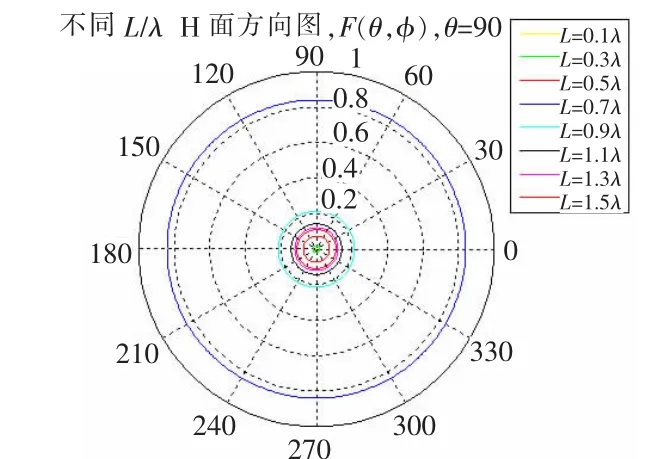
圖4 未歸一化的不同L/l的H面方向圖
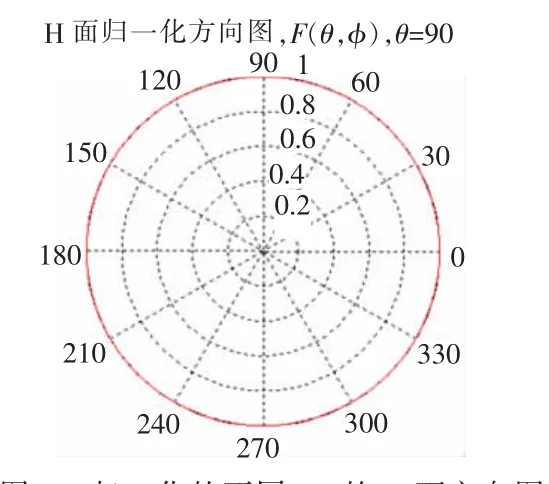
圖5 歸一化的不同L/l的H面方向圖
結果分析:
(4)L/l>1.25時,隨L/l增大,主瓣變窄變小,副瓣逐漸變大;L/l繼續增大,主瓣轉為副瓣,而原副瓣變為主瓣,見圖5。
2.3 功率增益
在本文的1.4節介紹了天線的增益,這里直接給出仿真結果,如圖6所示。
(2)當L/l<<1(短振子)時,方向函數和方向圖與電流元的近似相同。
(3)L/l<1.25時,最大輻射方向為
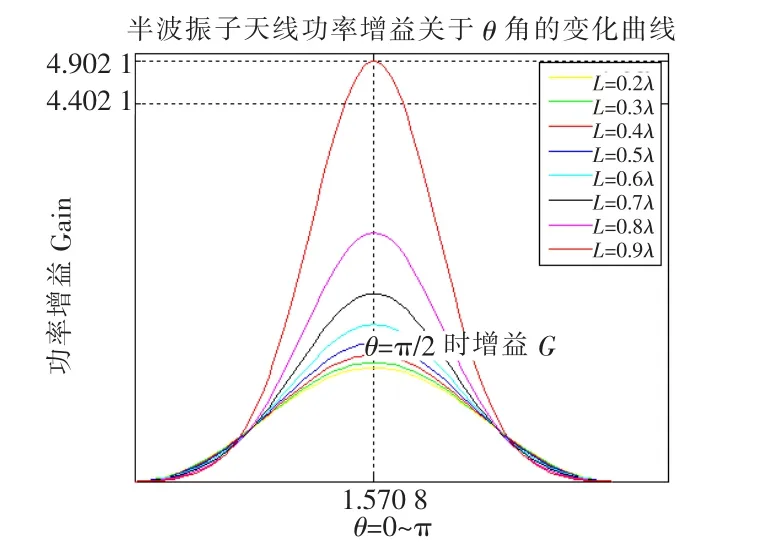
圖6 不同L/l的功率增益
從圖6可以看出,半波振子即為L=0.5l,觀察L= 0.5l的這條曲線可知,增益半波振子的增益G=1.646 1。
3 結論
本文利用HALLEN方法計算半波天線的電流分布、功率增益和方向圖,利用矩量法將HALLEN法的積分方程化為差分方程,將積分方程中積分化為有限求和,從而建立代數方程組,最后用MATLAB編程進行數值計算和可視化。
[1]謝處方,邱文杰.天線原理與設計[M].陜西:西北電訊工程學院出版社,1985.
[2]曹偉.Method of moments analysis for wire Antennas[Z].南京:南京郵電學院,2005.
[3]劉學觀,郭輝萍.微波技術與天線[M].西安:西安電子科技大學出版社,2001.
[4]徐立勤,曹偉.電磁場與電磁波理論[M].北京:北京郵電大學出版社,1999.
[5]SHAMSI M,RAZZAGHI M.Solution of Hallen′s integral equation usingmultiwavelets[J].Computer Physics Communication,2005,168(3):187-197.
[6]HALLEN E.Theoretical investigation into the transmitting and receiving qualities of antennas[J].Nova Acta Social Sciences,1938,3:1-44.
[7]張黎明,鄧阿麗,趙燕平.矩量法計算半波振子天線電流分布[J].艦船電子工程,2006(2):127-129.
[8]姜光興,曹偉,朱洪波.基于不同積分方程的線天線矩量法分析[J].南京郵電學院學報,2005,25(1):46-50.
[9]吳曉英,劉學觀.線天線輻射特性的矩量法分析[J].蘇州大學學報(工學版),2005,25(3):29-32.
[10]梁榮江.基于MATLAB分析矩量法在線天線中的應用[J].西安郵電學院學報,2009,14(1):49-56
[11]陳煒峰,胡蓉,余莉.基于HFSS球形偶極子輻射天線的結構優化[J].揚州大學學報(自然科學版),2013,16(2):52-56
[12]張志涌.精通MATLAB6.5版[M].北京:北京航空航天大學出版社,2003.
[13]呂英華.計算電磁學的數值方法[M].北京:清華大學出版社,2006.
Parameters calculate of half-w ave antenna based on HALLEN equation method
Xu Zengchun,Lu Zhou
(College of Electronic and Information Engineering,Nanjing Tech University,Nanjing 211816,China)
In modern electromagnetic engineering,for the boundary uncomplex problems,analytic method can get accurate solutions,but more complex boundary value problem cannot be answered by analytical method,so we need numerical methods.In this article we derive HALLEN equation method,and use MATLAB software to solve.The results can be very close to the analytical value,indicating its correctness.Moment of method for solving electromagnetic boundary value problems is an effective numerical method,and we use the moment of method to convert the integral equation of HALLEN method into differential equations and the integral equation into finite sums.Thus we establish algebraic equations,then use MATLAB programming to obtain the parameters and realize the simulation.Finally,some numerical results are compared with the corresponding analytical solutions.As a result,the validity of method-of-moments is validated.
method-of-moments;HALLEN method;half-wave antenna;MATLAB
TN823
A
1674-7720(2015)14-0061-03
2015-01-19)
徐曾春(1973-),女,本科,工程師,主要研究方向:信號處理。
連云港市科技支撐計劃(SH1110)
盧洲(1988-),通信作者,男,碩士研究生,主要研究方向:無線通信,信號處理。E-mail:luzhou2004@126.com。

