突發事件下的列車運行圖穩定性分析

劉 健，孟學雷,，王金霞

（1.蘭州交通大學 交通運輸學院，蘭州 730070；2.北京交通大學 軌道交通控制與安全國家重點實驗室，北京 100044)

研究與開發

突發事件下的列車運行圖穩定性分析

劉 健1，孟學雷1,2，王金霞1

（1.蘭州交通大學 交通運輸學院，蘭州 730070；2.北京交通大學 軌道交通控制與安全國家重點實驗室，北京 100044)

由于列車在運行過程中受突發事件的影響不能保證完全按列車運行圖行車，本文提出列車運行圖穩定性指標，引入元胞自動機（CA）模型對列車運行進行仿真，計算列車運行圖穩定性指標，以京滬高速鐵路為例進行列車運行仿真，通過列車實績運行圖，得到列車運行圖穩定性與突發事件的發生概率及列車運行最大速度之間的關系，設計列車在某突發概率情況下為保證列車運行圖的穩定性而采用的最大運行速度。提出了一種新的列車運行圖穩定性的分析方法，得到的在不同條件下的列車最大允許速度，對列車運行圖的編制及日常列車運行調度工作具有重要意義。

運行圖穩定性；元胞自動機；仿真分析；最大允許速度

列車運行圖是鐵路系統中列車運行的重要依據，是規定列車與車站、鐵路區段關系的重要技術文件，保證列車按列車運行圖行車對鐵路系統的正常運行起著至關重要的作用，在遇到突發情況下，由于一列列車受到干擾而引起的延遲傳播可能會對后續的列車造成不確定的影響，這就要求列車運行圖具有一定程度的穩定性，在突發事件發生時能保證后續列車盡快地恢復按列車運行圖行車，從而使損失降低到最小。其中，列車運行圖的穩定性是衡量這種能力的重要指標。

目前，國內外對列車運行圖穩定性方面進行過諸多研究，出現了多種計算列車運行圖穩定性的方法，一般是運用系統仿真的辦法來解決運行圖穩定性優化以及評價等問題，主要研究有以下幾個方面。

陳軍華[1～2]等將運行圖穩定性劃分為可靠性、魯棒性以及穩定性3個范疇，提出提高列車運行圖穩定性的措施方法，建立列車運行圖編制與評價系統框架；引入著色賦時Petri網對列車區間運行以及車站作業分別建模，結合列車運行圖進行適應度評價指標，以京津城際客運專線為例對列車運行圖穩定性進行評價；孟學雷[3]等構造了混合時間事件圖模型來模擬列車的運行，然后定義路網列車運行圖穩定性，給出優化路網列車運行圖穩定性的方法，重復模擬，直到得到滿意解，驗證了模型的可行性以及算法的高效性；Rob M.P. Goverde[4]運用極大代數的方法描述列車運行圖，并對運行圖的敏感性和魯棒性進行了分析，評估了列車運行圖的可實現性和穩定性；Xavier[5]在車站層面上提出運用多目標法評價列車運行圖穩定性。

在以往的研究中，學者們以仿真方法研究列車運行圖穩定性，預先設定一個延遲時間，列車以趕點的方式在區段中運行，觀察列車恢復正點需要的時間，用以計算“運行線恢復系數”，從而判定列車運行圖穩定性，本文引入元胞自動機模型進行列車運行仿真，將突發事件分布于列車運行的各個時間點，觀察該運行圖可承載突發事件的程度，分析影響列車運行圖穩定性因素以及各因素之間的關系。

1 元胞自動機（Cellular Automaton）簡介

自然界中存在著許多的復雜系統，而組成這些系統的結構可能非常簡單，但是由于各個結構之間存在著一定的耦合關系，從而表現出來整體的狀態極其復雜。傳統的建模方法試圖用數學模型去描述復雜性及其解決復雜性所引起的問題，對實際模型進行簡化，直到能用數學方法精確計算出結論，這種方法通常從系統表述開始就去掉了復雜性的本質，得到的結論與實際情況往往有很大偏差。元胞自動機采用自下而上的建模方法，具有抽象性、適應性以及自組織性的特點，特別適用于此類系統的仿真。

1992年，德國學者納高（Nagel）和斯查克爾伯格（Schreckenberg）提出了著名的NaSch模型，這個模型是根據Wolfram的184號模型推廣而來，在這個模型中，時間、空間和速度都被離散化，用以描述一些實際的交通現象。具體模型設置如下：

（1）元胞空間大小： 1?n的離散的格子，表示一條道路。

（2）元胞鄰居形式：由于是1?n的格子，所以個體元胞只有前后兩側的元胞作為鄰居，作為一輛汽車，則不能與前后發生追尾。

（3）元胞狀態：每個元胞或者是空的，或者被一輛車占據，當元胞被一輛車占據時，車的速度可以取0, 1, 2, …, vmax。

（4）更新規則：

a.加速：vn→min(vn+1, vmax)，此步驟描述司機總是期望以最大速度行駛的特點；

b.減速：vn→min(vn, dn)，描述的是司機為了避免與前車發生碰撞而采取的措施；

c.隨機慢化：概率p，vn→max(vn–1, 0)，描述的是由于各種不確定性因素而導致的汽車減速，比如路況不好，司機遇到一些情況等；

d.位置更新：xn→xn+vn，汽車按照調整后的速度向前行駛。

其中，xn、vn分別表示汽車n的位置和速度；dn=xn+1–xn–l表示汽車n與汽車n+1之間的空元胞數，l表示車輛長度。

2 基于元胞自動機的列車運行系統構建

將NaSch模型進行改進應用到鐵路運行系統中，列車在運行狀態下遇到突發狀況發生延誤，而列車期望以正點到達前方車站，在保證與前方列車安全距離的前提下加速，下面將列車軌道劃分為若干個大小相等的細胞，具體更新規則如下 。

2.1 確定突發事件的發生概率P

由于突發事件具有多樣性及復雜性等特點，本文將抽象的突發事件具體為某一個突發事件發生概率，以便于研究在突發事件情況下列車運行圖穩定性以及允許的列車最大速度之間的關系。其中， Sn(t)表示列車所處的環境，式（1）表示列車依據列車所在位置的環境狀況確定突發事件發生的概率。

（1） T＜T0（表示當前時刻列車還未晚點）

若vn＜，并且，則

（2） T＞T0（表示當前時刻列車已經晚點）

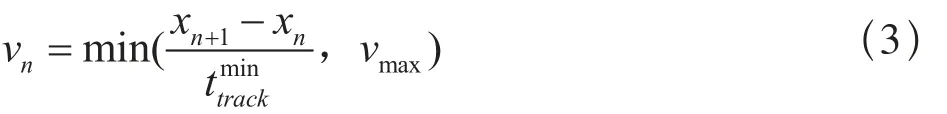
2.2 減速

式（4）表示當列車的速度大于它的正點速度時，列車需要減速至正點速度。

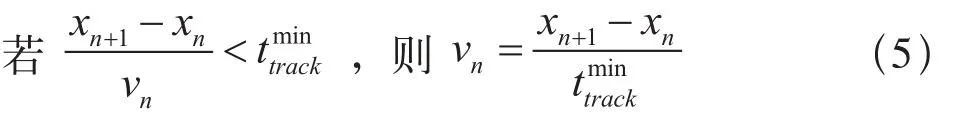
式（5）表示當兩列列車的追蹤時間小于最小追蹤間隔時間時，列車需要減速至保持它們最小追蹤間隔時間的速度。

若列車在當前時間步長的運行速度不滿足其加速以及減速的約束條件時，則列車在下一個時間步長仍然按照當前時間步長的運行速度運行。

2.3 隨機突發事件

其中，vrand表示列車因突發事件而降低的速度。由于元胞自動機其本身時間離散的特性，我們將隨機突發事件是否發生僅限于在當前時間判定，并且當前時間的判定并不影響下一個時間隨機突發事件的判定。也就是說，在某個隨機突發事件概率下，列車在各個離散時間點都會進行隨機突發事件是否發生的判定，這樣，列車在區段運行過程中是可以反映出列車由于受到突發事件的干擾而到達前方車站的延遲情況的。式（6）表示，當列車發生突發事件時，列車受到不確定因素影響在該時間步長內減速或停車，減速后的列車運行速度為max(vn–vrand, 0)。

2.4 位置更新列車按照調整后的速度向前行駛。

3 列車運行圖穩定性指標

運行圖穩定性用以描述運行圖的抗干擾能力以及在受到干擾以后的自我恢復能力，列車在受到外界隨機因素的干擾之后，最大程度的保證按圖行車，則認為該運行圖有較好的穩定性。具體公式如下：

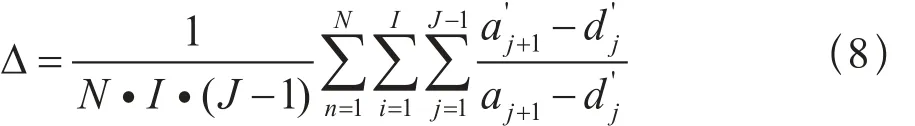
其中，N為仿真次數， n為第n次仿真；I表示運行圖中的列車數； i表示第i列列車； J表示列車經過的車站數目； j表示第j個車站； a'j+1表示列車到達j+1站的圖定時刻；aj+1表示列車到達j+1站的實際時刻；d'j表示列車離開j站的圖定時刻。

?表示的是經過N次仿真之后各個列車在各個車站的晚點率的平均值，用以說明列車運行圖的穩定性，其中， ?趨近1時， 運行圖趨近于穩定，當?=1時，列車完全正點運行，運行圖絕對穩定，反之，?越趨近于0時運行圖越趨于不穩定。

4 仿真分析

京滬高速鐵路由北京南站至上海虹橋站，縱貫北京、天津、上海3大直轄市和冀魯皖蘇4省，全程共設23個車站。

本文取京滬高速鐵路由北京南站到濟南西站，從7點～12點列車運行圖為例，途中經過的車站包括北京南站（0 km）、廊坊站（60 km）、天津南站（122 km）、滄州西站（210 km）、德州東站（314 km）、濟南西站（406 km），對該時間段列車運行進行仿真，通過仿真結果在各站的延遲時間計算各項指標來計算該運行圖穩定性指標。該段線路從北京南站至濟南西站共計406 km，定義每100 m為一個元胞，每個時間步長設定為1 min，本文從每列列車發車時間開始至列車駛離濟南西站為止，當前一列列車駛離濟南西站將不再影響后一列列車的速度。認為每個車站的到發線數目足夠，前車不影響后序列車的進站。京滬高速鐵路部分列車時刻如表1所示。

上述時刻表為早7點～12點之間出發的列車，共17個車次，為該時間段的列車運行圖如圖1所示。

當列車在運行過程中出現突發情況時，列車在站的越行方式會發生改變，如圖2所示。根據原定運行圖的規定，正常情況下列車在站的越行方式如圖2（a），列車b在A～B區段追蹤列車a，并在B站越行；當線路出現突發情況導致不能正常越行時，原有的越行方式就不再適用，列車b在A～B區段追蹤列車a，在B站卻不發生越行，繼續追蹤列車a，列車的運行方式即為圖2（b）。

本文采用MATLABR2009a為系統仿真平臺，每次實驗，系統自動生成一張實績運行圖并計算出穩定性指標,通過改變列車運行最大速度以及在運行過程中突發事件的發生概率值，概率選擇從0%～30%，以0.02為一個步長；最大速度選擇從300 km/h～350 km/h，以10為單位步長，圖3分別表示突發事件發生概率為10%，列車最大運行速度為330 km/h和350 km/h以及突發事件發生概率為20%，列車最大運行速度為330 km/h和350 km/h情況下的某次仿真的列車實績運行圖如圖3所示。

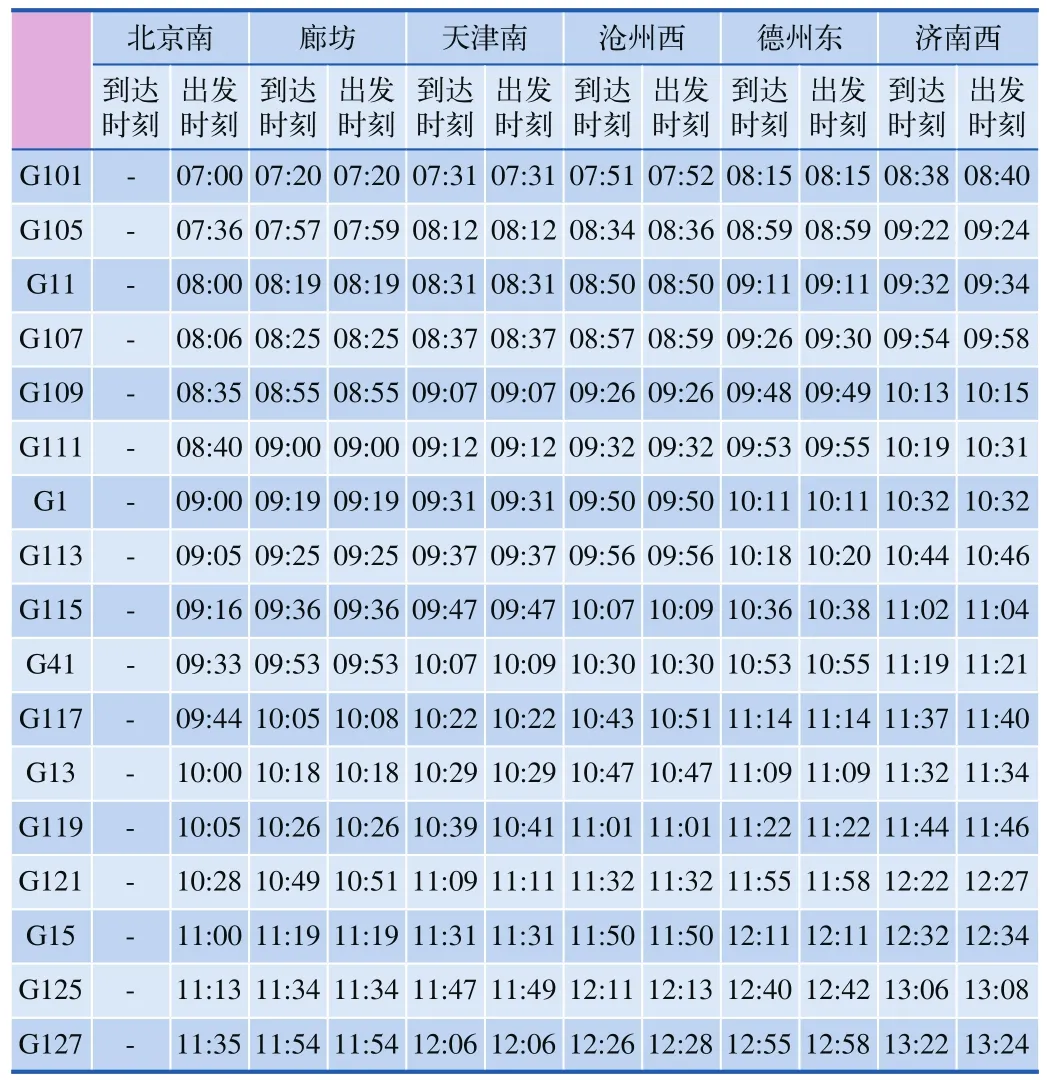
表1 京滬高速鐵路部分列車時刻表

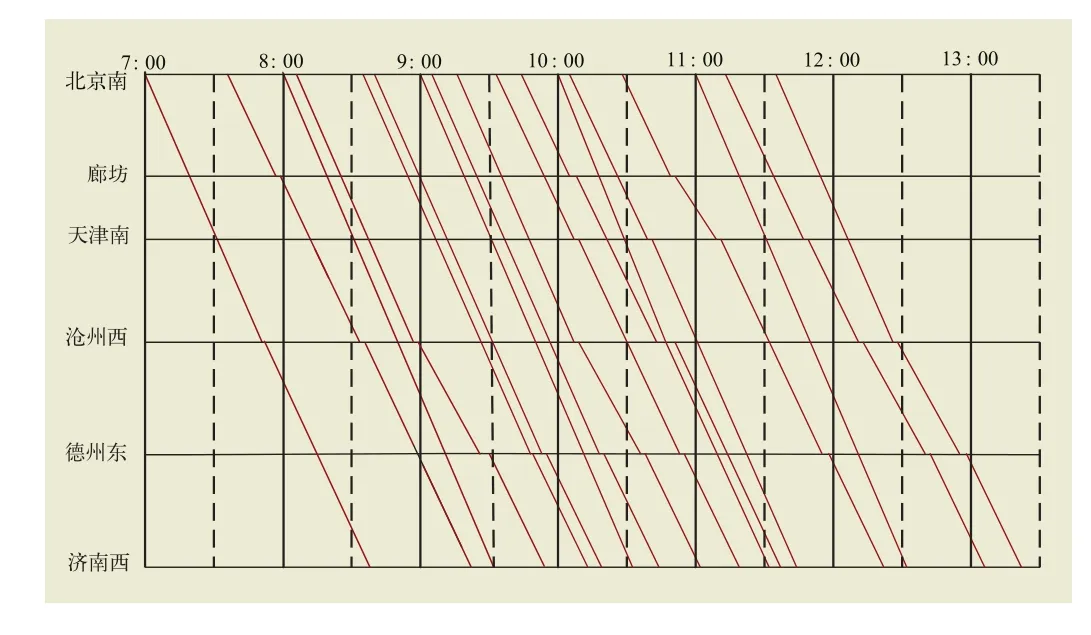
圖1 京滬高速鐵路部分列車運行圖

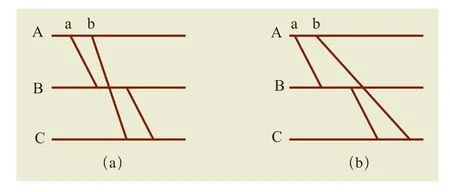
圖2 突發情況下列車運行式

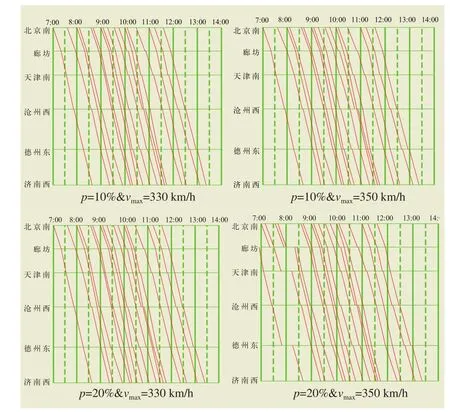
圖3 不同情況下的京滬高速鐵路列車實績運行圖

通過改變列車運行過程中的突發事件發生概率以及列車運行的最大速度，每種情況仿真30次，求其穩定性的平均值，總共仿真5 760次，建立離散點擬合三維曲面，得到列車運行的最大速度與運行過程中突發事件的發生概率與列車運行圖之間關系如圖4所示。

圖4 列車最大運行速度、突發事件概率與列車運行圖穩定性關系

由圖4中可知，隨著突發事件概率的增大以及列車最大運行速度的減小，列車運行圖穩定圖指標呈現遞減趨勢，并且隨著突發事件概率的增大，列車最大速度對運行圖穩定性指標的影響也逐漸增大。

一般地，當列車運行圖穩定性指標大于0.9時是符合列車運行正點率要求的，并且列車在區間運行過程中的突發事件發生概率應控制在20%及其以下。由仿真結果可知，當列車的最大運行速度達到330 km/h及其以上時可以達到該要求。

5 結束語

本文引入元胞自動機模型仿真列車在區段運行，定義每100 m為一個元胞長度，時間步長設定為1 min，仿真京滬高鐵從北京南站至濟南西站區段，仿真得到列車實績運行圖與該條件下列車運行圖穩定性指標。

（1）在突發事件發生概率達到28%以上時，G117次列車的運行延遲導致G13次列車不能正常越行的概率增加，從而造成大量延遲，根據實際情況，當突發事件發生概率達到28%時，可縮短G117次列車在滄州西車站的停站時間，從而降低G13次列車的延遲時間。

（2）建立以突發事件發生概率、列車最大運行速度與列車運行圖穩定性指標值為三維坐標值的散點擬合三維曲面，分析了突發事件發生概率、列車最大運行速度與列車運行圖穩定性指標之間的關系。隨著突發事件發生概率的增加以及列車最大運行速度的減少，列車運行圖穩定性指標呈現遞減趨勢，并且隨著突發事件發生概率的增加，列車最大運行速度對列車運行圖穩定性指標的影響也逐漸增大。

（3）通過分析突發事件發生概率、列車最大運行速度與列車運行圖穩定性指標的關系，得到了在一定的列車運行圖穩定性指標水平下列車最佳的最大運行速度，并且得到了優化后的列車運行圖。

（4）本文通過引入元胞自動機模型以及列車運行圖穩定性指標計算方法，結合京滬高速鐵路進行仿真分析，分析得到列車最佳的最大運行速度，對列車運行圖鋪畫以及列車運行調度工作具有重要意義。

[1] 陳軍華，張星臣，徐 彬，褚文君.高速鐵路列車運行圖穩定性及其影響因素分析[J].物流技術，2011，30（8）：81-84.

[2] 陳軍華，張星臣，徐 彬.基于著色賦時PETRI網的運行圖穩定性評價研究[J].系統仿真學報，2011，23（4）：770-773，816.

[3] Meng Xue-lei,Jia Li-min,QIN Yong,XU Jie.Hybrid Timed Event Graph Model for Networked Train Operation Simulation and Timetable Stability Optimization[J]. Lecture Notes in Electrical Engineering, Volume 287, 2014, pp 575-582.

[4] Rob M.P. Goverde. Railway timetable stability analysis using max-plus system theory[J]. Transportation Research Part B,2007,41(2):179-201.

[5] Delorme,Xavier;Gandibleux,Xavier;Rodriguez,Joaquín.Stability evaluation of a railway timetable at station level[J]. European Journal of Operational Research, 2009,195(3):780-790.

[6] 孟學雷，徐 杰 ，賈利民.列車運行圖穩定性研究綜述[J].鐵道科學與工程學報，2013，10（2）：96-102.

[7] 楊肇夏，胡安洲，李 菊，胡 克，董中英.列車運行圖動態性能及其指標體系的研究[J].中國鐵道學報，1993，15（4）：46-56.

[8] 彭其淵，朱松年，閻海峰．列車運行圖可調整度評價系統研究[J]．西南交通大學學報，1998，33（4）：367-371．

[9] Xuelei Meng，Bingmou Cui, Limin Jia, Yong Qinand Jie Xu.Networked Timetable Stability Improvement Based on a Bilevel Optimization Programming Model[J].Mathematical Problems in Engineering, 2014(4): 10.

[10] Xuelei Meng, Limin Jia. Train Timetable Stability Evaluation based on Analysis of Interior and Exterior Factors Information Entropy[J]. Applied Mathematics & Information Sciences. 2014,8(3): 1319-1325.

[11] M. Carey and S. Carville, Testing schedule performance and reliability for train stations[J]. Journal of the Operational Research Society, 2000, 51(6): 666-682.

[12] I.A.Hansen, Station capacity and stability of train operations.,in Proceeding of the 7th International Conference on Computers in Railways[J]. Computers in Railways, 2000,7(9): 809-816.

[13] X. Delorme, X. Gandibleux, and J. Rodriguez, Stability evaluation of a railway timetable at station level[J]. European Journal of Operational Research, 2009, 195(3): 780-789.

[14] O. Engelhardt-Funke and M. Kolonko, Analysing stability and investments in railway networks using advanced evolutionary algorithm[J]. International Transactions in Operational Research, 2004, 11(4): 381-394.

責任編輯 徐侃春

Stability analysis of train diagram in emergency

LIU Jian1, MENG Xuelei1,2, WANG Jinxia1
( 1. School of Traffc and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. State Key Laboratory of Rail Traffc Control and Safety, Beijing Jiaotong University, Beijing 100044, China )

When the train operation process was affect by emergency, the train couldn’t be fully guaranteed to operate with train diagram. The paper put forward the stability index of train diagram, introduced Cellular Automaton(CA) model to simulation of the train operation process, calculated the stability index of train diagram, took the Beijing-Shanghai High-speed Railway Line as an example to simulate the train operation, according to the actually train diagram, got the relationship among the emergency probability and the train maximum speed and train diagram stability, designed the train maximum speed in order to ensure the train diagram stability in the case of emergency probability, proposed a new analytical method for the train diagram stability, got maximum permissible speed in different conditions. It was with important signifcance for drawing up the train diagram and dispatching the train operation.

stability of train diagram; cellular automaton; simulation analysis; maximum permissible speed

U292.41∶TP39

A

1005-8451（2015）09-0001-05

2015-01-10

甘肅省自然科學基金資助項目（1310RJZA068）；國家自然科學基金項目（61263027）。

劉 健 ，在讀碩士研究生；孟學雷，副教授。