城市軌道交通進站客流量短時預測模型研究＊

劉美琪 焦朋朋 孫 拓

（北京建筑大學土木與交通工程學院，100044，北京∥第一作者，碩士研究生）

隨著城市軌道交通實時交通信息系統的日益完善，管理者需要掌握未來短時間內客流量的變化趨勢，以制定和實施交通管理計劃，這不僅可以使交通管理逐步走向智能化、動態化和信息化，還能提高運營效率，同時為出行者提供高效方便的服務。

在城市軌道交通日客流預測方面，文獻［1］利用馬爾科夫鏈改進了灰色模型；文獻［2］將神經網絡和支持向量機兩種方法融合在一起，得到了組合預測模型；文獻［3］則在前人研究的基礎上，建立了基于客流時序特征的神經網絡模型。在城市軌道交通短時客流預測方面，BP 神經網絡［4－5］與小波神經網絡［6］被引入組合模型。

非參數回歸模型（Nonparametric Regressive Model）與神經網絡模型同屬于無數學模型的預測方法，但多用于道路交通流短時預測。文獻［7］最早真正將非參數回歸的方法應用到了交通流量預測中。文獻［8］對傳統的非參數回歸進行了改進，運用變K 搜索算法和基于動態聚類和散列函數的歷史數據組織方式。文獻［9］利用該模型預測倫敦環路的交通量；文獻［10］則應用到了快速路行程速度的預測。此外，卡爾曼濾波［11］、目標導向的神經網絡算法［12］、模糊神經網絡［13］與貝葉斯組合神經網絡算法［14］均被引入預測模型中。

非參數回歸模型適用于非線性和非平穩性的數據序列，但很少應用于軌道交通客流量預測。因此，本文為預測每5 min的進站客流量，分別建立了K近鄰非參數回歸（NPR）、基于偏差修正系數的卡爾曼濾波（KF）以及貝葉斯組合（BCM）模型，通過對比分析各模型在早高峰、晚高峰、平峰時段和全天的預測誤差指標，發現K近鄰非參數回歸比其他模型的預測精度更高，對突發客流的處理能力更強。

1 預測模型

如圖1所示，首先應用NPR 預測某站點兩天的短時進站客流量，兩天的預測值是為組合模型做準備，算法主要分為4步：歷史數據準備及樣本數據庫生成、狀態向量定義、K近鄰搜索、預測算法。然后應用傳統卡爾曼濾波模型預測前一天的客流量，擬合偏差修正系數，將系數引入觀測方程并預測后一天的短時客流量。最后將前一天作為歷史特征天，后一天的各時段作為貝葉斯組合預測模型中的當前時段，分別計算誤差及貝葉斯權重，代入模型得到預測結果。

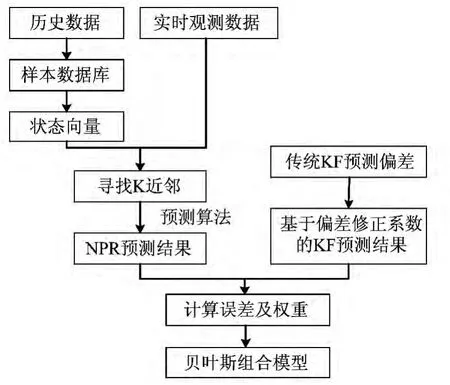
圖1 算法流程

1.1 NPR 模型

NPR 是應用很廣泛的一種非參數回歸算法，具有無參數、可移植、預測精度高等優點，它的誤差比較小，且誤差分布情況良好。

1.1.1 歷史數據準備及樣本數據庫生成

樣本數據庫由表示系統狀態的全部歷史觀測資料組成，NPR 預測的效果和質量直接取決于樣本數據庫的質量。交通系統狀態的特征蘊含在歷史數據中，歷史數據越多，越有利于非參數回歸更加真實且完整地表達系統狀態的特征，越有利于得到精確的預測值。樣本數據庫是動態的，它會隨著觀測數據的生成而不斷更新，因此這是一個實時庫與歷史庫相結合的復合數據庫。

1.1.2 狀態向量的定義

在交通領域，狀態向量是指與預測站點當前時段的流量相關聯的影響因素組成的向量。地鐵站點吸引的客流量與路段交通量不同，它沒有明確的上下游路段，沒有信號燈，但是與預測站點相鄰的其它站點的布置會影響客流量的分布及到達規律。所以在本文中，引入預測站點與其它站點之間的相關性分析，以相關系數ρAB的大小來確定狀態向量中的相關站點數，同時狀態向量還應包括預測站點前m個時段（t，t－1，t－2，…，t－m）的流量數據，m的取值可以通過計算m階自相關系數ρm來確定。

將站點A連續n個時間段的客流量看作時間序列｛V1，A，…，Vn，A｝，站點B的客流量時間序列為｛V1，B，…，Vn，B｝，兩站點之間的相關系數

式中：

VA——站點A時間序列的平均值；

VB——站點B時間序列的平均值。

計算自相關系數時，將預測站點連續n個時間段的進站流量看作時間序列｛V1，…，Vn｝，把這組時間序列分解成｛V1，…，Vm＋1｝，｛V2，…，Vm＋2｝…｛Vn－k，…，Vn｝共n－m組子序列，設其m階自相關系數

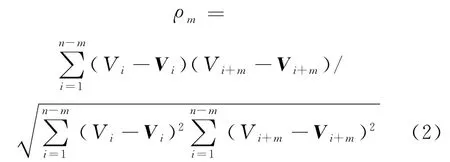
式中：

Vi——第i個子序列的平均值。

1.1.3 K 近鄰搜索

K近鄰法則是一種基于數據的非參數回歸方法，它并非建立一種數學預測模型，而是尋找與當前狀態向量相匹配的K個最近鄰的數據，并以該K個數據的下一時段的數據為基礎，對站點下一時段的值進行預測。

在樣本數據庫中搜索與實時數據相匹配的數據系列時，主要采用歐氏距離作為主要指標，即當前狀態向量的各分量與歷史狀態向量中各分量的離差平方和的開方值，以此作為匹配距離，表達式如下：

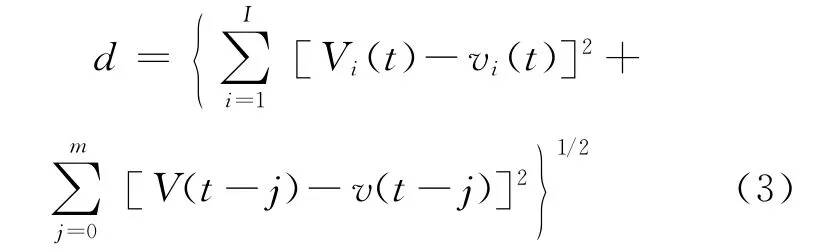
式中：

I——與研究站點相關的其它站點集合；

m——狀態向量中研究站點前m個時段；

Vi（t）——站點i在時段t的進站流量；

vi（t）——歷史數據中站點i在時段t的進站流量；

V（t－j）——研究站點當前狀態t－j時段的進站流量；

v（t－j）——研究站點歷史數據中的進站流量。

1.1.4 預測算法

設Vi（t）是時段t第i個近鄰的進站客流量，di是其與當前狀態向量之間的歐氏距離，則下一時段的客流量

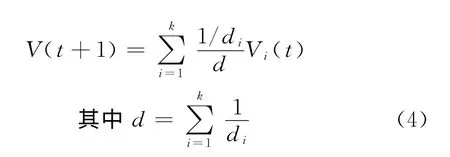
1.2 基于偏差修正系數的卡爾曼濾波模型

傳統卡爾曼濾波模型盡管遞推效率高，但由于其對歷史信息的利用率較低，導致預測結果穩定性不強，所以為了提高其精度，在改進的觀測方程中引入了偏差修正系數ω。地鐵進站客流量隨著時間序列存在平峰和高峰的變化規律。用傳統卡爾曼濾波模型預測歷史特征天的短時客流量，發現預測偏差（實際值減去預測值的絕對值）也存在平峰、高峰、先增后減的變化規律，用二次拋物線來擬合這種趨勢。拋物線通過原點與偏差最大點，令a、b為常數，表達式為：

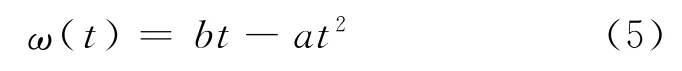
在不同條件下，修正系數的函數表達式不同，但是均與偏差的變化規律有關，所以修正系數的函數需要基于歷史數據擬合得到。然后建立基于偏差修正系數的卡爾曼濾波模型，該模型包括狀態變量、狀態轉移方程和觀測方程3個核心部分。

狀態變量確定為Q（t），即時段t預測站點的實際進站流量。狀態轉移方程為：

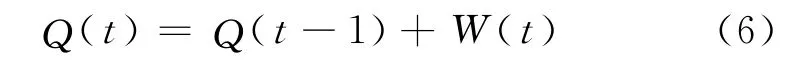
其中W（t）是狀態方程的高斯白噪聲序列。觀測方程為：

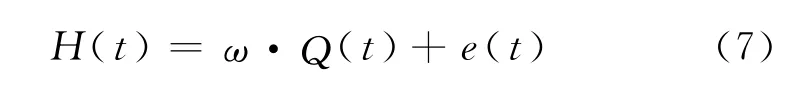
其中H（t）為時段t地鐵站點的歷史平均客流量；e（t）是高斯白噪聲序列。

1.3 貝葉斯組合預測模型

根據貝葉斯定理，建立組合模型：

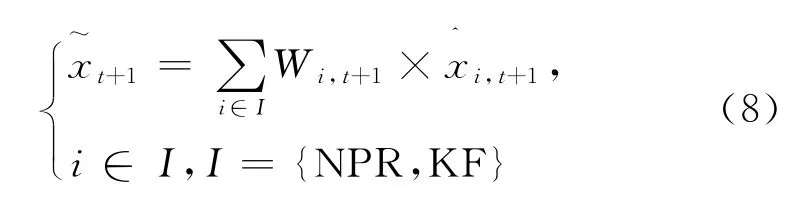
式中：

I——模型的集合；

NPR——K近鄰非參數回歸模型；

KF——代表基于偏差修正系數的卡爾曼濾波模型；

Wi，t＋1——模型i在t＋1時刻的權重。

2 實證研究

基礎數據是北京市地鐵13號線2013年11月份的進站客流，站點以編號來表示，分別為21、23、25、27、29、33、35、37、39、41、43、45、47、49和51。編號順序按照實際站點順序排列。本文以25號站點為研究對象，5 min為一個時段，從4：45至24：00，共分為231個時段。卡爾曼濾波模型和貝葉斯組合預測模型需要歷史偏差數據，所以將11月21日（星期四）定為歷史特征天，11月28日（星期四）確定為研究天。本節以NPR 的預測過程為重點，首先論述狀態向量及K值的確定過程，然后對比分析28日各模型全天、早晚高峰和平峰時的預測誤差。

2.1 確定狀態向量及K值

2.1.1 狀態向量的定義

狀態向量通常選擇與預測站點的交通狀態最為相關的因素，因此本文選擇相鄰站點當前時段和預測站點前m個時段的進站客流量，通過計算相關系數ρAB及ρm來確定，相關系數取值在－1和1之間，且絕對值越大相關性越大，如圖2所示。

25站點與21、23、27和49的相關系數絕對值都超過了0.9，但是49站距25站比較遠，所以排除這個選擇，以21、23和27站的當前時段客流量V21，V23，V27為狀態分量。此外，狀態向量還包括預測站點前m個時段，如圖3所示，通過比較25站點自相關系數ρm絕對值的大小，確定m＝2。綜上，狀態向量X（t）＝｛V21（t），V23（t），V27（t），V25（t－1），V25（t－2）｝。

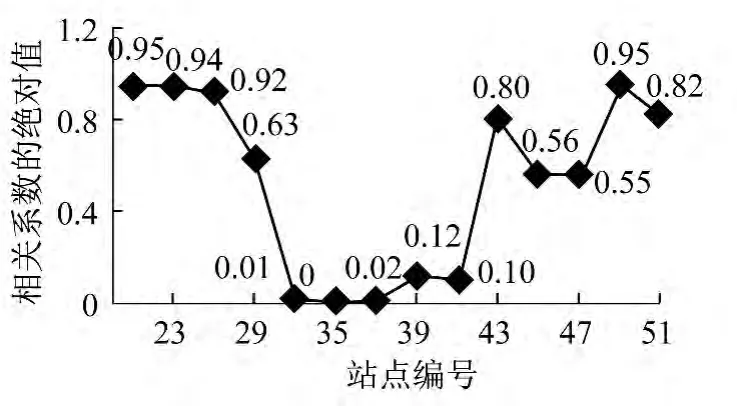
圖2 25站點與其它站的相關性對比

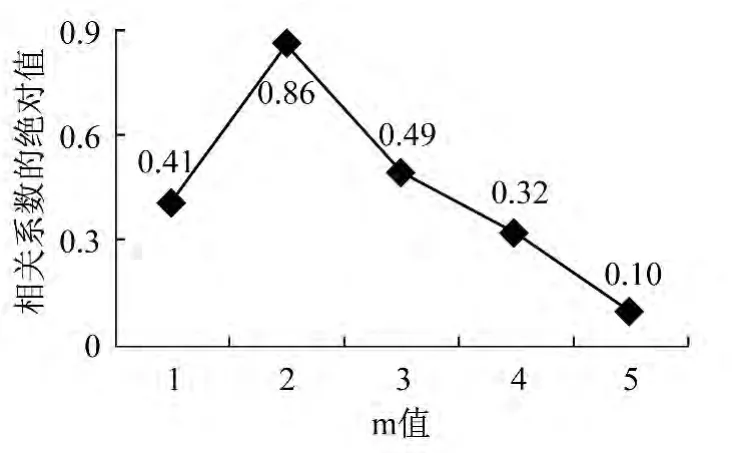
圖3 25站點自相關系數

2.1.2K值的選取

狀態向量確定后，在樣本數據庫中尋找和當前狀態特征相似的K個近鄰，然后進行預測。一般是通過逐漸增加K值，觀察其對預測結果的影響，來確定最優K值。評價指標選取均方根誤差ERMS、標準均方根誤差在ENRMS、平均絕對百分誤差EMAP和平均百分比誤差EMP。令時段i的預測值為Pi，實測值為Ai，表達式如下：

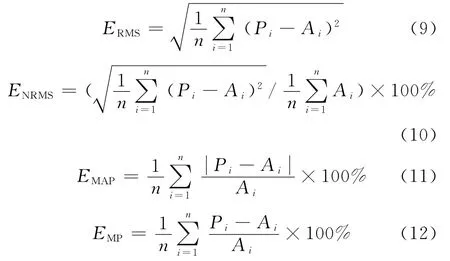
K取值從1至5，預測早晨4：45至凌晨24：00的進站客流量，并計算誤差指標。如表1所示，當K＝2時ERMS、ENRMS、EMP值最小，EMP的值與最小值只相差1%，即0.01，所以K＝2是最優值。

2.2 各模型預測結果

2.2.1 誤差指標對比

對全天5：00—24：00每5 min的客流量進行預測，誤差指標如表2所示。

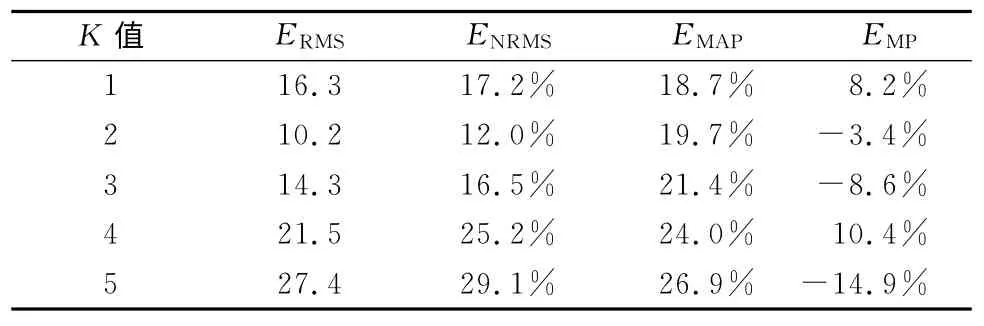
表1 不同K 值的誤差指標

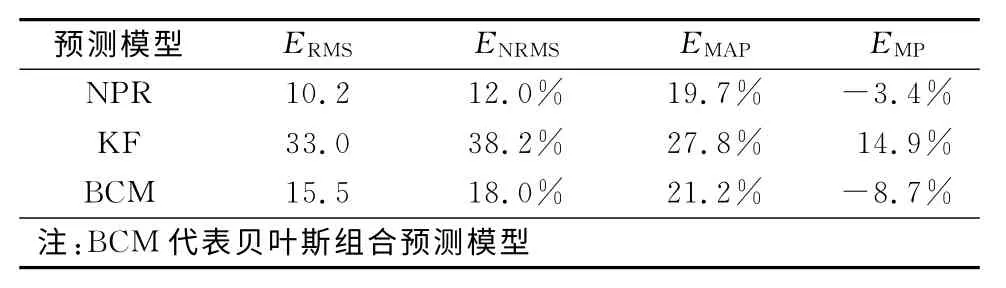
表2 模型誤差指標

可以發現NPR 的預測精度最高，KF 的預測精度最低。由于BCM 權值分配規則是誤差大的權值較小，誤差小的權值較大，所以BCM 各項誤差指標值在兩子模型之間，且平穩性較好。

一般城市軌道交通的早高峰為7：00—9：00，平峰為11：00—13：00，晚高峰為17：00—19：00。預測每5 min的客流量，對比三類模型在不同時間段的ERMS，如表3所示。

由表3 可見：早高峰期間，NPR 的ERMS值最小，預測精度最高；KF 與BCM 的EPMS差值相近。平峰期間，BCM 的EPMS精度最高，說明在客流量小且平穩度增高的情況下該模型預測精度會提高。晚高峰時KF的EPMS值遠大于早高峰、平峰與全天的EPMS，說明面對客流量的猛增與大幅度震蕩，該模型預測穩定性較差。

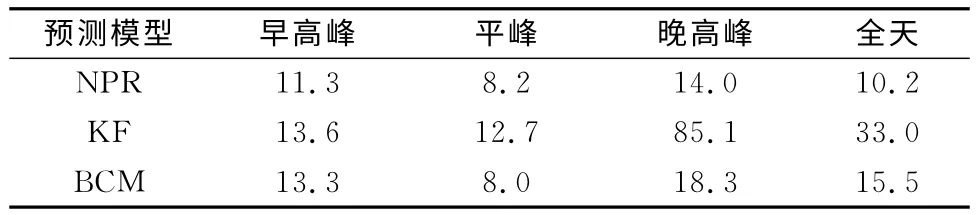
表3 不同時間段的ERMS指標

2.2.2 流量誤差對比

如圖4所示，早7：00—9：00，KF 和BCM 預測流量誤差波動性越來越大，BCM 的流量誤差大體上在20以下，NPR 的流量誤差則不超過20，且大多在10以內，說明了NPR 的適用性。

從圖5可以看出，盡管平峰時客流的到達率會相對比較平均，KF 的流量誤差仍很不平穩。BCM的流量誤差則隨時間趨于平穩，而且在平峰的后期，其流量誤差是三類模型中最小的，所以BCM 更適用于預測短時流量少又平穩的時段。

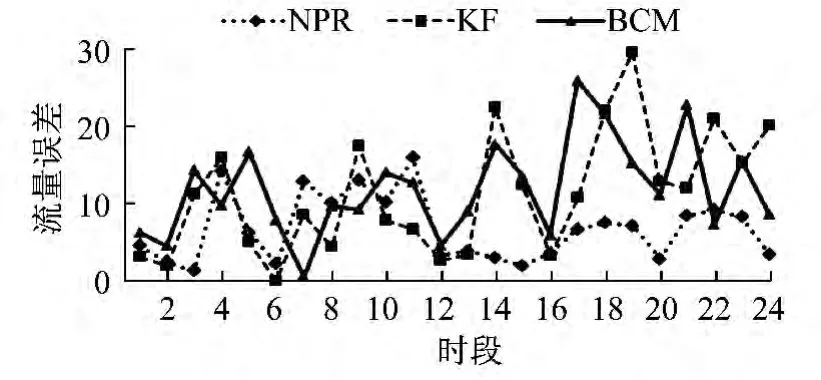
圖4 早高峰流量誤差

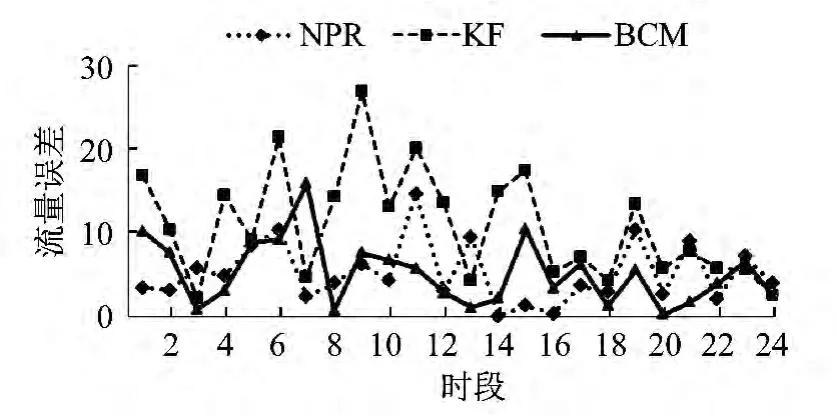
圖5 平峰流量誤差

如圖6所示：晚高峰KF的誤差明顯大于NPR和BCM，甚至達到了80；BCM 的流量誤差在NPR 和KF之間，說明BCM 融合了兩個子模型的優點和缺點。計算貝葉斯權重就是為了中和預測精度，但這也決定了它不會比最優的子模型預測精度更高。

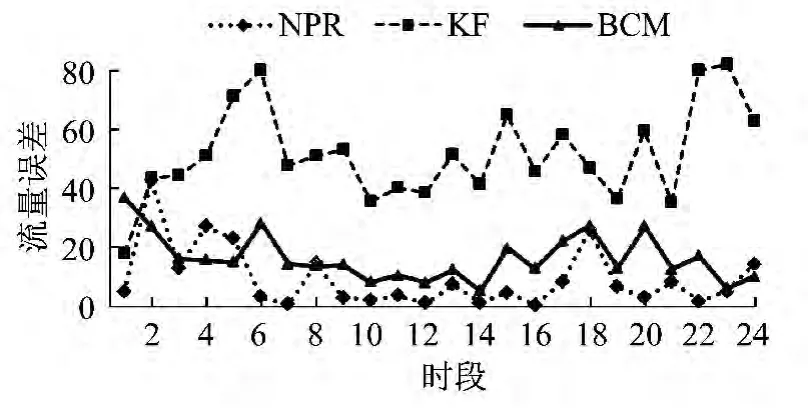
圖6 晚高峰流量誤差

3 結語

NPR 模型是基于歷史數據的預測方法，沒有固定的數學模型，應用條件是要有充足的、實時的觀測數據，一般不少于一個月，其特點是預測精度依賴于數據量的大小。對于換乘站，如果有該線路相鄰各站點的歷史數據，可以真實且完整地表達客流狀態的不同特征，從樣本數據庫中能夠搜索到近鄰點，就可以利用該模型得到精確的進站客流預測結果。而KF模型一般只需要預測站點一周的歷史數據，沒有其他的影響因素，所以同樣可用于換乘站。

通過研究發現，NPR 模型的優點是應對突發事件的能力很強、預測準確性和誤差分布較好，且不需要先驗知識和大量的參數識別；但是其搜索速度較慢，參數調整也需要時間。KF 模型優點是算法簡單，計算效率很高，對歷史數據的需求量不大且應用廣泛，但是其預測誤差較大。在一天中不同時段的預測穩定性也不高，誤差波動性大。BCM 模型是利用加權把多個單一預測模型線性組合起來，權值是根據每個子模型前一時期的預測誤差計算條件概率得出的，其優點是提高了模型預測的穩定性。

進一步研究應嘗試改進上述模型，使其精度和穩定性可以達到客流量實時預測的需求；另外可以探尋進站量、出站量、換乘量與斷面客流量等參數之間的動態變化關系，從城市軌道交通客流形成機理方面構建新的預測模型。

［1］謝輝，董德存，歐冬秀，等.軌道交通短期客流預測方法及其算法研究［J］.現代城市軌道交通，2011（3）：96.

［2］毛靜.城市軌道交通客流短期預測方法及實證研究［D］.北京：北京交通大學，2012.

［3］四兵鋒，何九冉，任華玲，等.基于時序特征的城市軌道交通客流預測［J］.北京交通大學學報，2014，38（3）：1.

［4］董升偉.基于改進BP神經網絡的軌道交通短時客流預測方法研究［D］.北京：北京交通大學，2013.

［5］Wei Y，Chen M C.Forecasting the short－term metro passenger flow with empirical mode decomposition and neural networks［J］.Transportation Research：Part C，2012，21（1）：148.

［6］鄒巍，陸百川，鄧捷，等.基于遺傳算法與小波神經網絡的客流預測研究［J］.武漢理工大學學報：交通科學與工程版，2014，38（5）：1148.

［7］Davis G，Nihan N.Nonparametric regression and short－term freeway traffic forecasting［J］.Journal of Transportation Engineering，1991，117（2）：178.

［8］宮曉燕，湯淑明.基于非參數回歸的短時交通流量預測與事件檢測綜合算法［J］.中國公路學報，2003，16（1）：28.

［9］Clark S.Traffic prediction using multivariate nonparametric regression［J］.Journal of Transportation Engineering，2003，129（2）：161.

［10］翁劍成，榮建，任福田，等.基于非參數回歸的快速路行程速度短期預測算法［J］.公路交通科技，2007，24（3）：93.

［11］Okutani I，Seephanedes Y J.Dynamic prediction of traffic volume through Kalman filtering theory［J］.Transportation Research Part B：Methodological，1984，18（1）：1.

［12］Hussein D.An object－oriented neural network approach to short－term traffic forecasting［J］.European Journal of Operational Research，2001（131）：253.

［13］Yin H，Wong S C，Xu J，et al.Urban traffic flow prediction using a fuzzy－neural approach［J］.Transportation Research C，2002，10（2）：85.

［14］Zheng W Z，Lee D，SHI Q X.Short－term freeway traffic flow prediction：Bayesian combined neural network approach［J］.Journal of Transportation Engineering，2006，132（2）：114.

［15］王奕，徐瑞華.基于周期時變特點的城市軌道交通短期客流預測研究［J］.城市軌道交通研究，2010（1）：46.