輪軌非線性幾何接觸對鐵道車輛穩定性影響的研究＊

張 海 周新建 王成國 肖 乾 林鳳濤

（1.華東交通大學機電工程學院，330013，南昌；2.中國鐵道科學研究院鐵道科學技術研究發展中心，100081，北京；3.華東交通大學現代軌道車輛研究所，330013，南昌∥第一作者，講師）

鐵道車輛的導向運動主要由輪軌關系所決定，因此，輪軌關系也是研究鐵道車輛運動的基礎之一。在輪軌關系中，輪對又是最基礎的組成部分。傳統的輪對有一些獨有的特征：輪對由一根剛性的軸連接在一起，因此輪對上的2個車輪都是按照同一個角速度旋轉，并且它們之間的距離是不變的；車輪輪緣保持在鋼軌內側邊緣，且輪緣與鋼軌內側邊緣橫向間隙通常在7～10 mm 左右；車輪踏面在橫截面上都具有一定的曲率；同樣，鋼軌頂面在橫截面上也具有一定的曲率［1］。盡管在理論上輪軌接觸的幾何關系是確定的，但是它具有很強的非線性特征，在高速運行條件下其對鐵道車輛行車穩定性有很大的影響。

1 輪軌滾動接觸幾何準線性表示

依據學者Maurer的表述，作為車輪截面半徑RW、鋼軌頂側面連接曲線半徑RR、接觸角δ0、名義滾動圓距的一半e0和名義滾動圓半徑r0的線性表述如圖1所示。

為了更為簡單、高效地描述輪軌的幾何接觸狀態，準線性輪軌接觸模型一般有以下3個參數：等效錐度λe、接觸角參數ε和滾動參數σ。

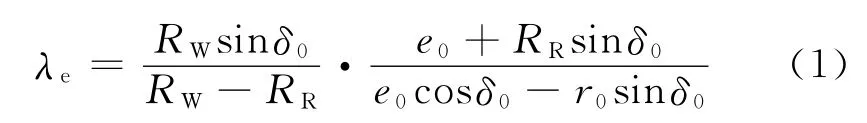
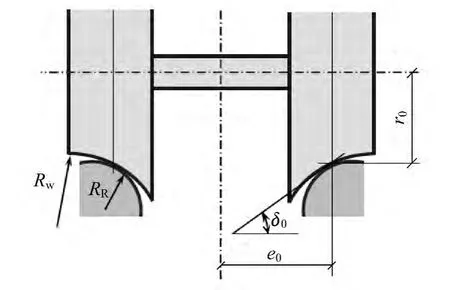
圖1 輪軌接觸線性化表述模型

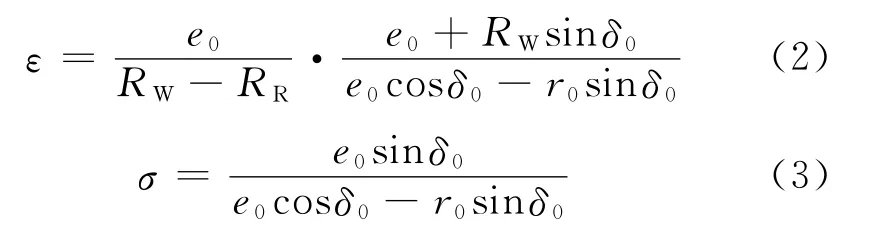
假設δ0角很小（sinδ0≈δ0，cosδ0≈1），那么式（1）就可簡化為

從式（4）可以看出，λe受到δ0和輪／軌輪廓匹配的影響。

準線性的輪軌接觸模型參數可以通過簡諧線性法進行計算。這種線性化不僅考慮在輪軌平衡位置的非常微小的位移，而且還考慮輪軌之間微小間隙下的特殊位移。學者Polach使用準線性的輪軌接觸來計算臨界速度（車輛從某速度運行時受外部激勵產生振動后，如果振動的幅值不斷衰減，則認為車輛運行穩定，若振動出現等幅周期振蕩，則此速度稱為車輛的臨界速度），并討論了ε角和σ變量對臨界速度的敏感性。總的來說，相對于λe對車輛運行穩定性影響的敏感性，ε對車輛運行穩定性影響的敏感性低很多［2］。

等效錐度可以方便反映出輪軌接觸的典型幾何特征，因此得到了廣泛的應用。目前，國際上主要應用以下4種計算等效錐度的方法：

1）簡諧線性法；

2）國際鐵 路聯盟 標準 UIC 519 附 錄 B［3］Klingel式的等效線性法；

3）國際鐵路聯盟標準UIC519附錄C 的滾動圓半徑差的線性回歸法；

4）UK 線性法。

不同方法計算的等效錐度存在差異［4］。輪對橫移量3 mm 時的等效錐度定義為名義等效錐度［5］。本文使用Adams／Rail軟件中的RSGEO 工具包計算等效錐度，采用了簡諧線性法。等效錐度λe的確定要滿足以下條件：線性的左右車輪滾動圓半徑差與非線性的左右車輪滾動圓半徑差之間差值的平方應在一個正弦波（y＝y0sinτ，其中，y為輪對橫移值，y0為橫移幅值，τ為時間變量）運動周期內的積分為最小，如式（5）所示。

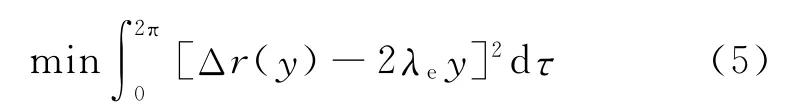
式中：

Δr（y）——左右車輪滾動圓非線性半徑差。

對λe求導，得到

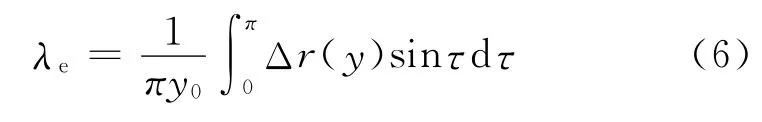
這樣將非線性關系的Δr（y）折算成線性關系就稱為等效線性化，當為諧波運動時稱為簡諧線性化。

2 輪軌接觸非線性幾何參數

現在按輪對橫移幅值3 mm 時的等效錐度數值作為輪軌接觸幾何參數。在鐵道車輛安全性實踐中，等效錐度能反映有關的有用信息。但是等效錐度并沒有考慮輪軌滾動接觸的非線性幾何特性［4，6－7］。

為了解決些問題，有兩個參數被提出來用于描述輪軌滾動接觸非線性幾何特性。

1）能級參數：即等效錐度λe。

2）非線性參數λN：其為等效錐度隨輪對橫移幅值變化曲線的斜率。

依據國際上最新的研究成果輪對橫移幅值為2 mm 和4 mm 下的錐度數值被用于配合幅值3 mm下等效錐度來評價車輛運行穩定性。這三個錐度數值被用來計算非線性參數λN，這也能描述等效錐度隨輪對橫移幅值的變化情況。在最新版的UIC518標準中，λN常使用輪對橫移幅值為2 mm 和4 mm下的等效錐度增加量與輪對橫移幅值增加量的比值表示，記為λN，1如式（7）所示。

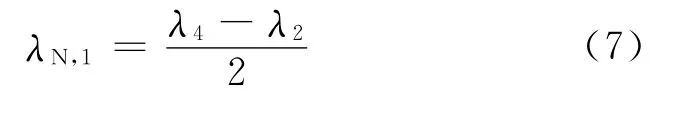
式中：

λ2——輪對橫移幅值2 mm 下的等效錐度；

λ4——輪對橫移幅值4 mm 下的等效錐度。

3 輪軌接觸非線性幾何參數對車輛運行穩定性的影響

為了分析非線性參數對車輛運行穩定性的影響，選取在2010年7月18日和9月5日分別測量的車輪踏面磨耗型面LMaWear1和LMaWear2以及新輪型面LMA。其中，型面LMaWear1為運行10.1萬km 時 CRH2103 型車2號車1位車輪型面，型面LMaWear2為運行19.6萬km 時CRH2103型2號車1位車輪型面，測量數據來自于Danmark公司的MiniProf測量系統。將這3種車輪踏面磨耗型面與新軌CHN60型鋼軌進行匹配，研究輪軌接觸的幾何參數對車輪運行穩定性的影響。

3.1 輪軌接觸幾何分析

型面 LMA／CHN60 型新軌匹配、型面 LMa Wear1／CHN60型新軌匹配、型面LMaWear2／CHN60型新軌匹配時的輪軌接觸點分布如圖2～圖4所示。

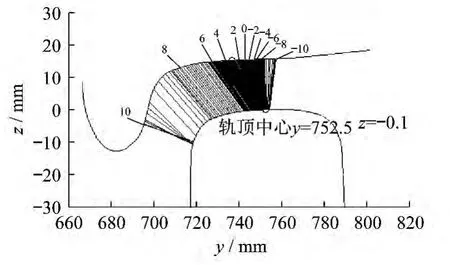
圖2 型面LMA／CHN60型新軌匹配時輪軌接觸點分布

從圖中2可以發現，型面LMA／CHN60型新軌匹配時輪軌接觸點分布均勻，車輪接觸點主要分布在踏面平緩處，只有當輪對橫移量超過8 mm 時，接觸點迅速進入輪緣。

從圖3和圖4可以發現：磨耗后的型面匹配下輪對型面上接觸點明顯向輪緣根部移動，鋼軌上的接觸點也向軌頂邊緣處移動；同時接觸點變化的跳躍點明顯增多，一方面會使得輪軌磨耗不均勻，另一方面還會降低車輛的運行品質。

由圖5可知，型面LMA／CHN60型新軌匹配時等效錐度曲線隨輪對橫移幅值的增大而緩慢遞增，當輪對橫移幅值超過8 mm 后，等效錐度急劇變大，這可以從圖4發現原因，此時的接觸點快速進入輪緣根部。而磨耗后型面匹配時，等效錐度經歷了先增大再降低，最后再次增大的過程，而且隨著運行公里數增加，磨耗不斷增加，等效錐度曲線呈現出“凹”形分布，而且不斷加大“凹”的程度。

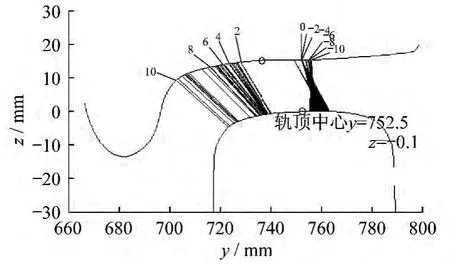
圖3 型面LMaWear1／CHN60型新軌匹配時輪軌接觸點分布

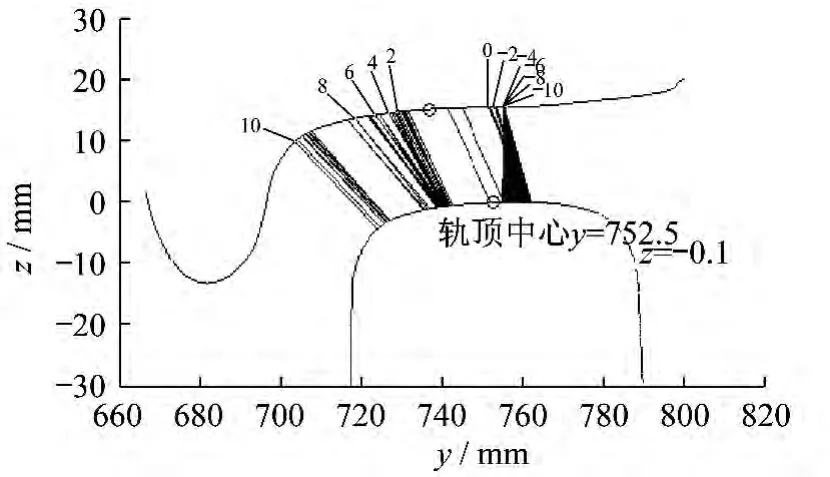
圖4 型面LMaWear2／CHN60型新軌匹配時輪軌接觸點分布

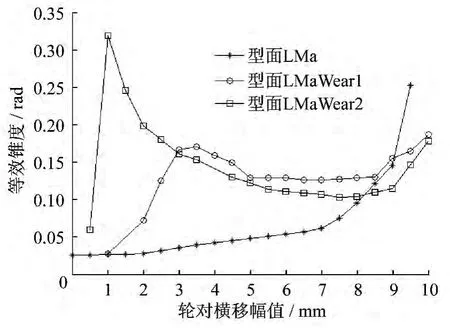
圖5 3組不同輪軌匹配的等效錐度比較

型面LMA、LMaWear1、LMaWear2的名義等效錐度λ3分別為0.035、0.165、0.163 rad。按照式（7）計 算 出λN，1，分 別 為 0.007 3、0.043 5 和－0.026 5，如表1所示。

3.2 輪軌接觸非線性幾何參數對車輛運行穩定性的影響

建立CRH2型車輛動力學模型，將輪軌匹配分別 改 為 LMA／CHN60、 LMaWear1／CHN60、LMaWear2／CHN60。其仿真結果的車輛行駛速度分叉曲線如圖6、圖7、圖8所示。發現隨著名義等效錐度的減小，會使得分叉曲線向右移動，即線性臨界速度和非線性臨界速度增大；而在名義等效錐度大致相同的時候，λN，1的變化對車輛的動力學響應有比較大的變化，隨著λN，1減小，速度分叉圖中輪對橫移幅值小的臨界速度明顯減小。

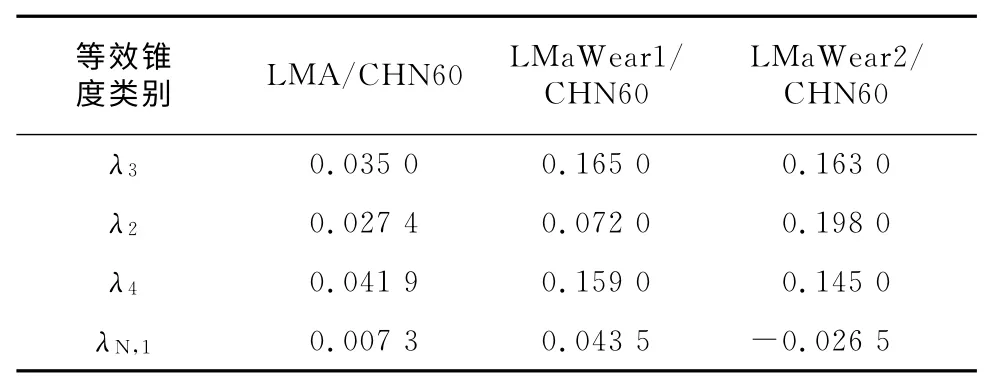
表1 3組不同的輪軌匹配錐度表 rad

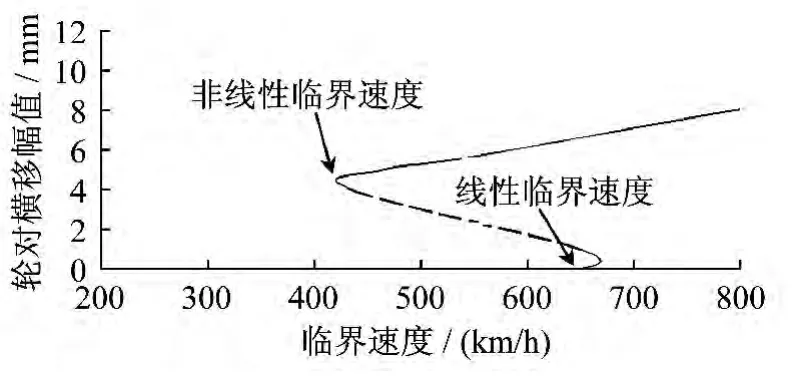
圖6 LMA／CHN60匹配下車輛速度分叉圖

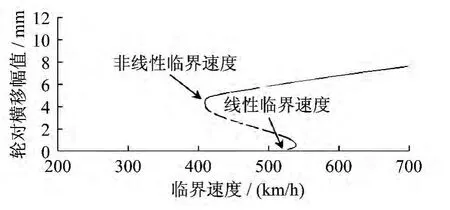
圖7 LMaWear1／CHN60匹配下車輛速度分叉圖

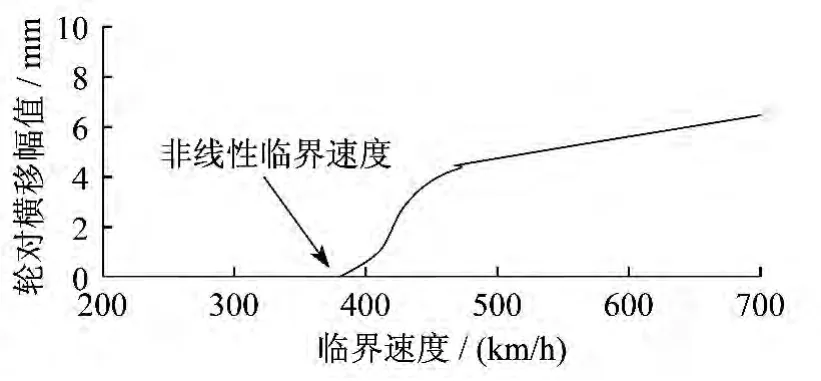
圖8 LMaWear2／CHN60匹配下車輛速度分叉圖

3.3 實測數據分析

從現場試驗數據（車輛運行速度為300 km／h，里程從 K99.311 km 至 K102.672 km）的分析也能得到相似的結論，磨耗嚴重的輪軌型面匹配下的車體和構架振動情況都急劇惡化，同時輪軸橫向力均方根值也增加了21.1%，如表2所示。圖9、圖10、圖11和圖12分別顯示的是車體橫向振動加速度對比圖、車體豎向振動加速度對比圖、構架橫向振動加速度對比圖及輪軸橫向力對比圖。

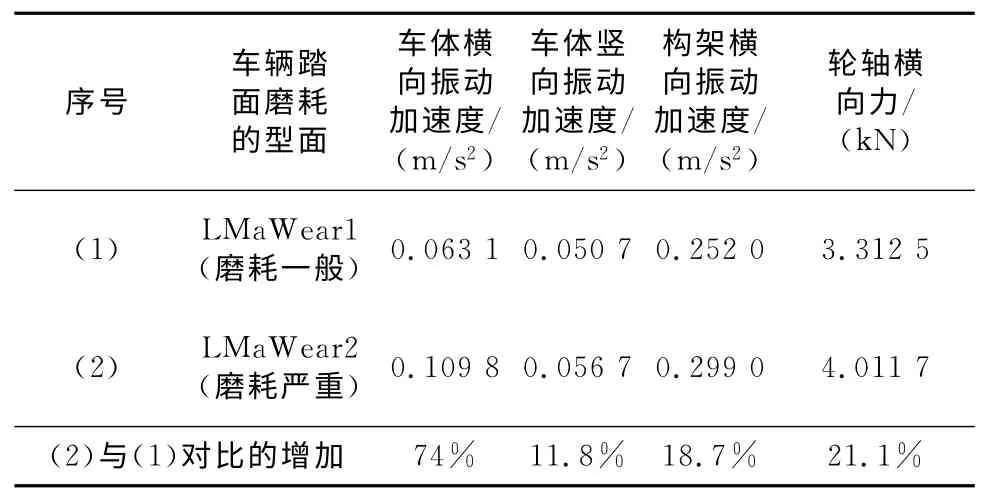
表2 現場試驗數據均方根值比較

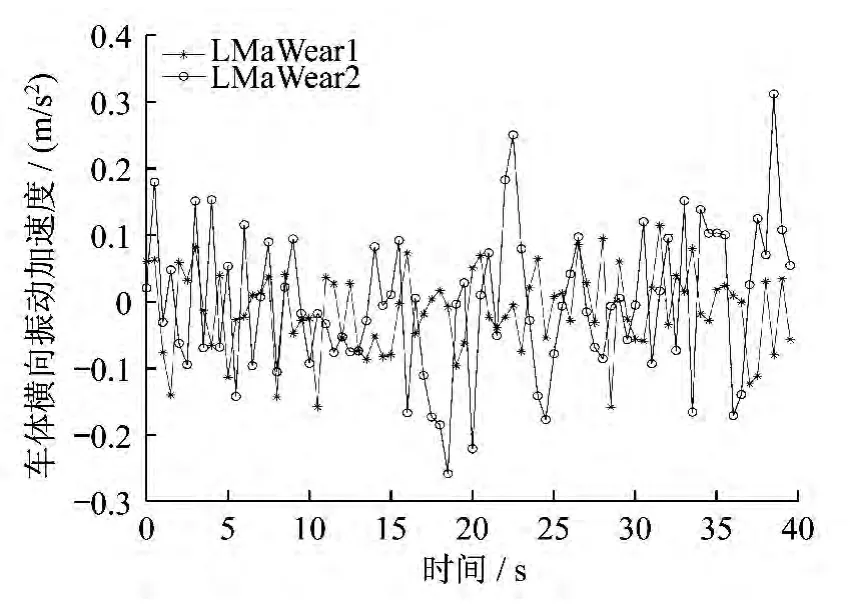
圖9 車體橫向振動加速度對比圖

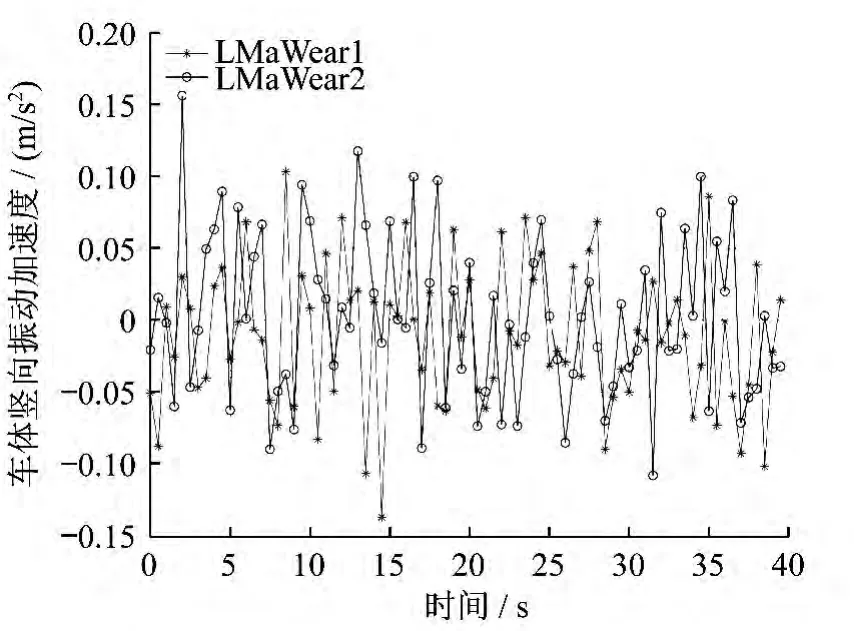
圖10 車體豎向振動加速度對比圖

4 結論

本文分析了輪軌滾動接觸的幾何線性和非線性參數的表達，并通過車輛速度分叉圖討論了它們對車輛運行穩定性的影響，并得出以下結論：

1）隨著名義等效錐度的減小，會使線性臨界速度和非線性臨界速度增大。

2）在名義等效錐度大致相同時，非線性參數的變化對車輛的動力學響應有比較大影響，隨著λN，1的減小，車輛速度分叉圖中輪對橫移幅值小的臨界速度明顯減小。

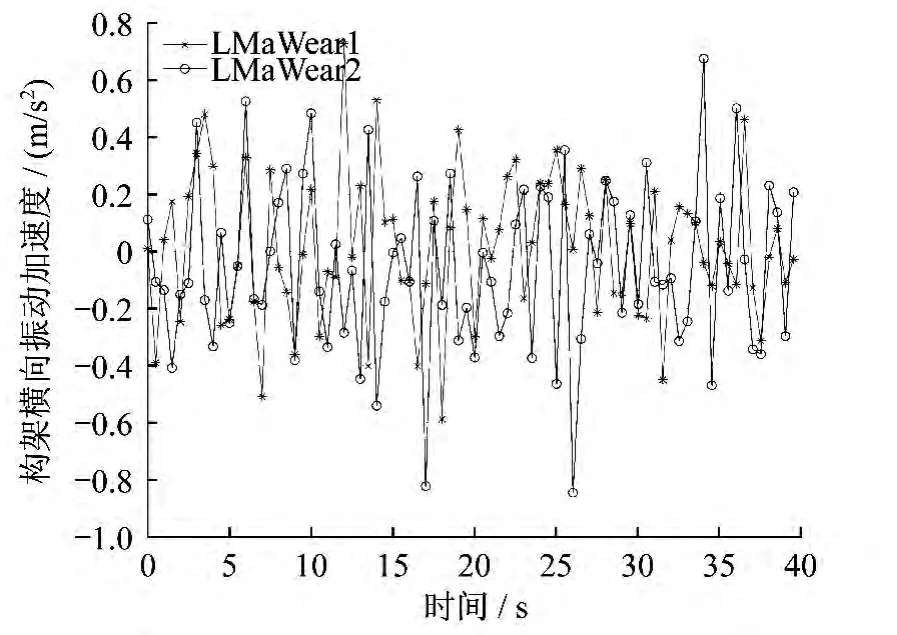
圖11 構架橫向振動加速度對比圖

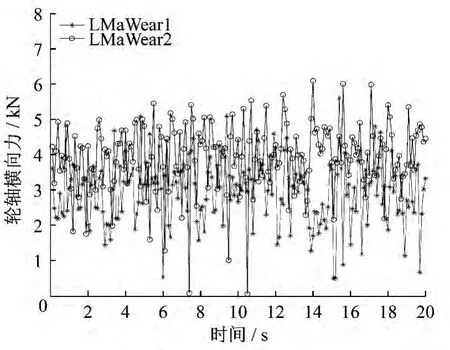
圖12 輪軸橫向力對比圖

3）從現場試驗數據的分析發現，磨耗嚴重的輪軌型面匹配下的車體和構架振動情況都急劇惡化，同時輪軸橫向力均方根值也大幅增加。

［1］柳擁軍.高速輪軌接觸幾何學及高速輪軌幾何型面優化的研究［D］.北京；鐵道部科學研究院，1999.

［2］Polach O.Comparability of the non－linear and linearized stability assessment during railway vehicle design［J］.Vehicle System Dynamics，2006，44（Supplyment）：129.

［3］UIC519 Method for determining the equivalent conicity［S］.Paris：International Union of Railway，2004.

［4］Polach O.Chapacteristic parameters of nonlinear wheel／Rail contact geometry［C］∥Berg M Trigell，A S.Proceedings of the 21st IAVSD Symposium，Stockholm，2009：95.

［5］Neetter H，Schupp G，Rulka W.New Aspects of contact modelling and validation within multibody system simulation of railway vehicles［J］.Vehicle System Dynamics，1998，28（Suppl.）：246.

［6］Polach O.Application of nonlinear stability analysis in railway vehicle industry［M］∥ Thomsen P.G.True H.Nonsmooth Problems in Vehicle System Dynamics.New York，Springer，2010：15.

［7］劉宏友，曾京，呂可維.高速客車蛇行運動Hopf分叉的研究［J］.工程力學，2005（6）：224.