隨行裝藥的響應面分析
祁臣勇,朱 林
(1.中北大學,太原 030051;2.瀘州北方化學工業有限公司,四川瀘州 646003)
彈丸初速是火炮的重要彈道指標之一,提高初速可以增加火炮射程、提高火炮的威力。隨行裝藥技術是一種能有效提高彈丸初速的技術,其結構與現有火炮結構兼容,只需要改變彈藥結構,一旦關鍵技術取得突破,可很快進入工程應用。隨行裝藥的關鍵技術包括:隨行技術、點火延遲時間的控制技術和高燃速火藥技術[1]。目前,隨行裝藥的關鍵因素研究主要采取單因素法[2-4],不能很好的預測最佳條件,更無法揭示因素之間的交互作用。
響應面法是數學和統計學結合的產物[5],目前已廣泛應用于生物學和統計學專業研究中,但在隨行裝藥領域少見報道,響應面法能根據某些點的值繪制出相應曲面,通過對模型的數學解析得出最優的參數組合,而傳統方法得出的最優點只是正交中所列元素各水平的最優組合,并不是全局的真正最優組合[6]。
本文使用design expert 軟件中的響應面法研究隨行裝藥結構的關鍵因素和他們之間的交互作用。利用固體隨行裝藥零維內彈道模型進行數值模擬計算,研究彈丸初速和最大膛壓隨點火延遲時間、隨行藥燃速和隨行藥量的變化趨勢,計算出點火延遲時間、隨行藥燃速和隨行藥量的最優解。
1 數值模擬的模型和計算方法
數值模擬計算采用固體隨行裝藥零維內彈道模型。經試驗驗證,此模型計算結果與實驗結果吻合較好,可預測隨行裝藥的內彈道性能[3]。假設隨行裝藥試驗在30 mm 火炮上進行,使用四階龍格庫塔法編寫隨行裝藥零維內彈道模型計算程序,利用程序進行數值模擬計算。
1)主裝藥藥型函數

2)主裝藥燃速方程
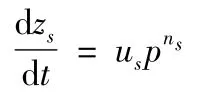
3)隨行藥藥型函數

4)隨行藥燃速方程
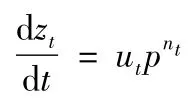
5)彈丸行程與速度的關系式

6)彈丸運動方程
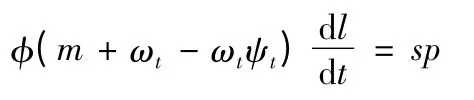
7)內彈道基本方程
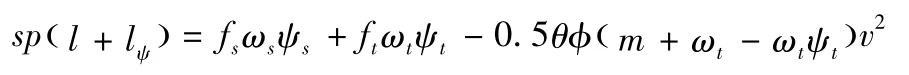
其中:
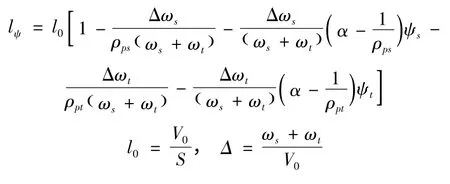
2 結果與分析
2.1 響應面法方案設計及結果
根據國內外學者在隨行裝藥試驗和理論研究所取得的成果[2-4,7],選取點火延遲時間、隨行藥燃速和隨行藥量作為考察因素,為了計算方便用隨行藥壓力全沖量來表征隨行藥燃速系數。使用Box-Behnken 法(BBD)設計優化分析方案,利用程序進行數值模擬計算。試驗方案和模擬計算結果如表1 所示。

表1 BBD 試驗方案及模擬結果
2.2 數據處理和顯著性分析
將參數進行編碼轉換,使因子區域轉化為中心在原點的“立方體”,實現參數的無量綱化。設第i 個變量zi的變化范圍是[z1i,z2i],z0i為區間中心點,編碼轉換為

經過編碼轉換后,各變量的編碼如表2 所示。

表2 各因素編碼
采用二階模型對數值計算結果的編碼進行多元回歸擬合,得到以彈丸初速V 和最大膛壓P 為目標的兩個二次回歸多項式:


上述方程中的變量取值為實際值的編碼,編碼取值區間為(-1,1)。對回歸多項式進行方差分析,檢驗多項式和各因子的顯著性,結果如表3、表4 所示。
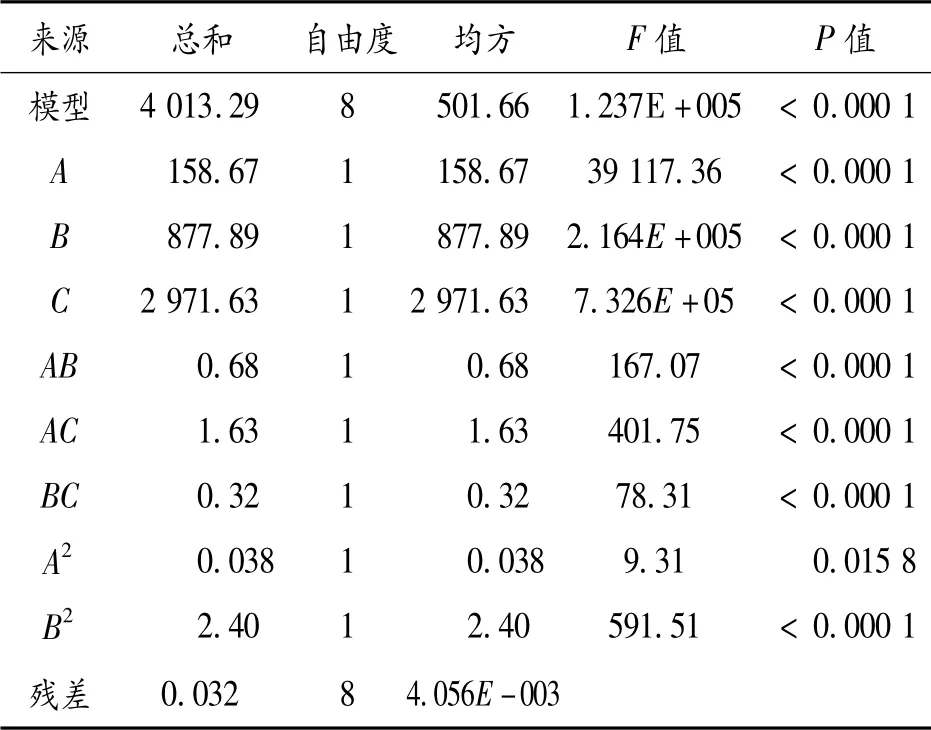
表3 彈丸初速多項式方差分析表
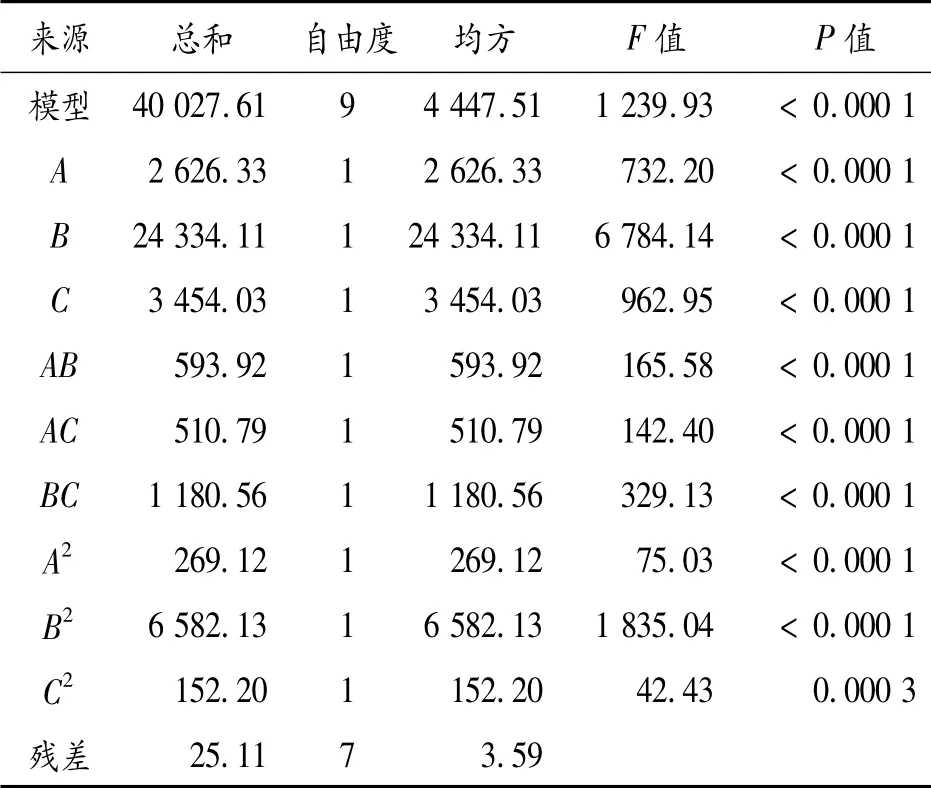
表4 最大膛壓多項式方差分析表
分析結果顯示:分析方案所設定的3 個因素均為影響彈丸初速和最大膛壓的關鍵因素。在設計范圍內,速度模型的P <0. 000 1,校正決定系數為1. 000 0,預測相關系數為0.999 9,說明選用的模型回歸顯著,速度多項式可以解釋100%響應值的變化[8]。最大膛壓模型的P <0.000 1,校正決定系數為0.998 6,預測相關系數為0.990 0,說明最大膛壓選用的模型回歸顯著,膛壓多項式可以解釋99.86%響應值的變化[8]。圖1、圖2 分別為彈丸初速和最大膛壓的內學生化殘差正態分布圖,兩圖中數據分布接近于對角線,說明殘差的分布接近于正態分布。由圖可知,真實值都落在預測值上或對稱分布在預測值兩側,說明2 個模型與真實值擬合良好。綜上所述,在設定區間內多項式的預測值與實際值吻合良好。多項式的設定區間如表5 所示。
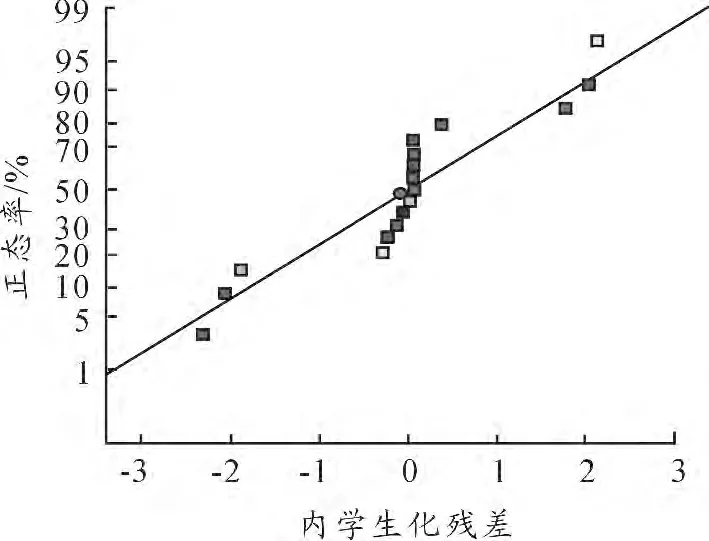
圖1 彈丸初速的內學生化殘差正態分布
圖2 最大膛壓的內學生化殘差正態分布

表5 多項式的設定范圍
2.3 分析單因素對內彈道性能的影響
圖3、圖4 分別表示3 種因素在設計中心點附近變動時彈丸初速和最大膛壓的變化趨勢。由圖3、圖4 可看出:
1)點火延遲時間減小,最大膛壓和彈丸初速逐漸增高。主要原因是:第一,隨行藥點火越早,火藥燃氣做功時間越長,彈丸初速越高;第二,隨行藥點火越早,主裝藥與隨行藥燃燒的壓力疊加效應越顯著,最大膛壓越高;第三,隨行藥點火越早,膛內壓力越高,隨行藥燃速越快,膛內壓力增加越快,裝藥利用系數越高,彈丸初速越大。
2)隨行裝藥壓力全沖量越大,彈丸初速越低,最大膛壓越低。當火藥弧厚一定時,壓力全沖量越小,火藥燃速越快。由此可知隨行藥燃速越快,彈丸初速越高。主要原因是:第一,隨行藥燃速越快,填充彈后真空的燃氣越多,彈后空間的壓力差越小,彈后壓力越高,火藥燃氣對彈丸做功越多,彈丸初速越高;第二,高燃速隨行藥燃燒生成的氣體,在氣固交界面上形成較大的推力,該推力與彈丸底部附近的氣體壓力相結合,對彈丸的做功能力增強,彈丸初速提高。
3)隨著隨行藥量的增加,彈丸初速和最大膛壓增高。

圖3 因素對彈丸初速擾動圖

圖4 因素對最大膛壓擾動圖
2.4 分析因素間交互作用對內彈道性能的影響
根據表1 和表2,結合方程(2)和方程(3),對各操作因素之間關系兩兩作圖,平面和三維結果分別如圖5 ~8 所示,圖中未出現的參數均設為0 水平。
圖5 ~8 反映了分析因素之間的交互作用。圖5(a)、圖7(a)反映延遲點火時間和隨行藥壓力全沖量對彈丸初速的交互作用。由圖可知,點火延遲時間和隨行藥壓力全沖量均與彈丸初速負相關,但壓力全沖量方向等值線斜率更大,表明壓力全沖量的變化對彈丸速度的影響比點火延遲時間對彈丸初速的影響大。圖5(b)、圖7(b)反映了點火延遲時間和隨行藥量對彈丸初速的交互作用。結果顯示,彈丸初速隨著點火延遲時間增加而減小,隨著隨行藥量的增加而增大,但隨行藥量的影響更顯著。若點火延遲時間取1.77 ms 且其他因素取零水平,隨行藥量27 g 時彈丸初速為923.719 m/s,隨行藥量增加到33 g 時彈丸初速接近950 m/s。說明隨行藥量對彈丸初速影響大。圖5(c)、圖7(c)反映了隨行藥壓力全沖量和隨行藥量對彈丸初速的交互作用。圖中響應面方程的平面等值線的變化趨勢與圖5(b)、圖7(b)相似,可知彈丸初速與隨行藥量正相關,與隨行藥壓力全沖量負相關,且隨行藥量對彈丸初速的影響比壓力全沖量的影響大。由上述分析可知,點火延遲時間、隨行藥壓力全沖量和隨行藥量對隨行裝藥結構的彈丸初速均有顯著的影響,按影響大小的排序:隨行藥量>隨行藥壓力全沖量>點火延遲時間。圖6(a)、圖8(a)反應了點火延遲時間和隨行藥壓力全沖量對最大膛壓的交互作用。結果表明,最大膛壓隨點火延遲時間的增大而減小,隨著隨行藥壓力全沖量的逐漸減小,最大膛壓先略有減小后逐漸增大,且增加趨勢越來越顯著。這說明兩因素之間有明顯的交互作用,且最優值位于點火延遲時間A >1.76 ms,隨行藥壓力全沖量B >66 kPa·s 的范圍內。圖6(b)、圖8(b)反映點火延遲時間和隨行藥量之間的交互作用。結果表明,點火延遲時間和隨行藥量對最大膛壓都有影響,但隨行藥量的影響更大。當隨行藥量逐漸增加時,最大膛壓逐漸增大,且增加的速度越來越快。隨行藥大于27 g 時最大膛壓隨著點火延遲時間的增加而減小,當隨行藥量小于27 g 時隨著點火延遲時間的增加,最大膛壓先減小后逐漸增加。這說明兩因素之間有較強的交互作用。圖6(c)、圖8(c)反映隨行藥壓力全沖量和隨行藥量之間的交互作用。圖中響應面方程平面等值線的分布規律與圖6(b)、圖8(b)相同,可看出兩因素之間有較強的交互作用,隨行藥壓力全沖量對最大膛壓的影響大于隨行藥量對最大膛壓的影響。由以上分析可知,點火延遲時間、隨行藥壓力全沖量和隨行藥量對隨行裝藥的最大膛壓均有較大影響,且因素之間的交互作用顯著。按影響大小的排序為:隨行藥壓力全沖量>隨行藥量>點火延遲時間。
2.5 模型的參數優化和驗證
根據表1 的數據以及建立的數學模型,輸入求優化解的限定條件和優化目標,利用design expert 軟件即可求出區域優化解。求各因素編碼Xi∈[-1,1] 且P <310 MPa 時彈丸初速的最大值。Design expert 求出的優化解為延遲點火時間1.80 ms,隨行藥壓力全沖量75.03 kPa·s,隨行藥量35 g。
為了驗證響應面回歸模型的有效性,變換因素水平利用內彈道程序進行模擬計算,結果如表6 所示。可以看出,在設定區間范圍內模型預測值與實驗值的最大相對誤差不超過1%,說明模型對實驗結果具有良好的預測效果。依據實驗2 的結果,在優化條件下,彈丸初速為948.591 m/s,最大膛壓307.25 MPa,這一結果比在同一隨行藥量下非優化實驗的結果提高了接近5%,說明該模型對于實驗具有較好的指導意義。

表6 響應面模型的驗證

圖5 彈丸初速的響應面方程的平面等值線
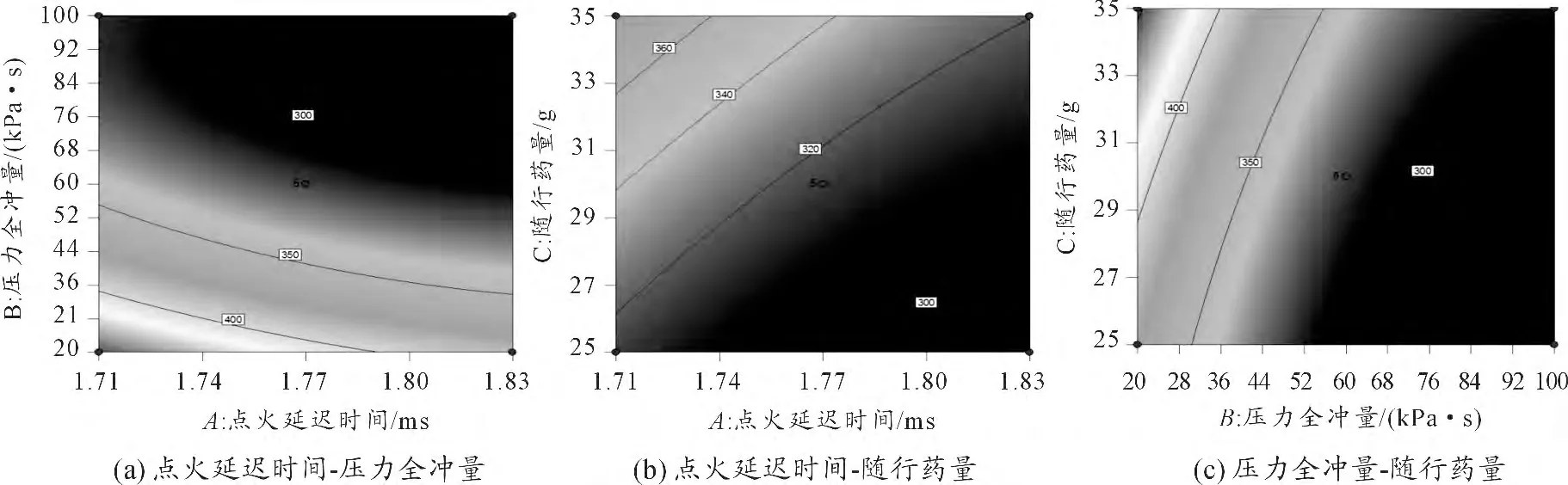
圖6 最大膛壓的響應面方程的平面等值線
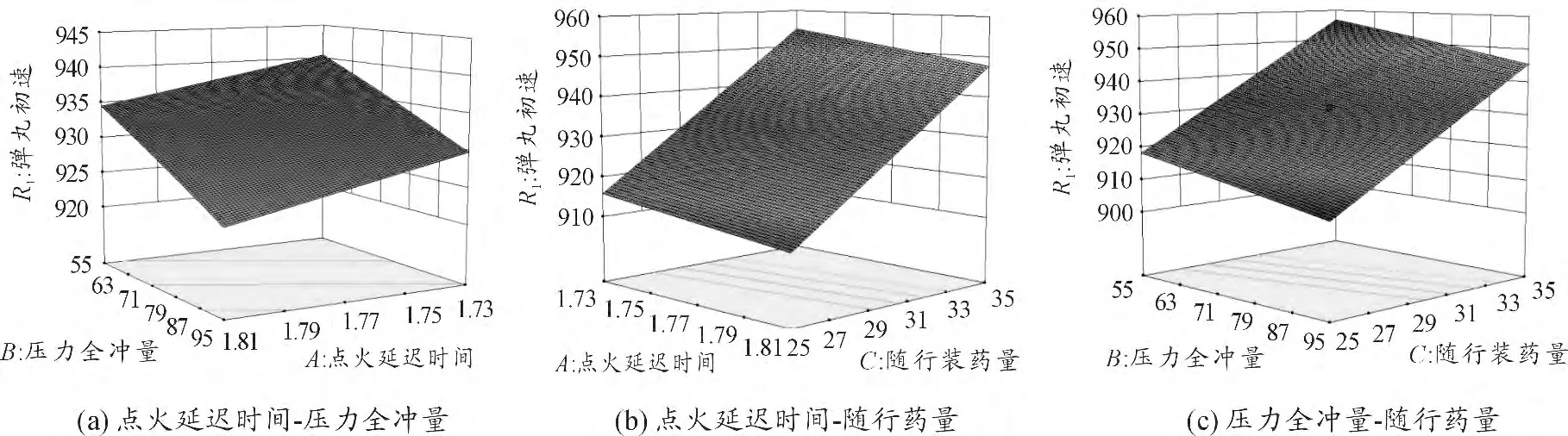
圖7 彈丸初速的響應面方程的等值曲面圖
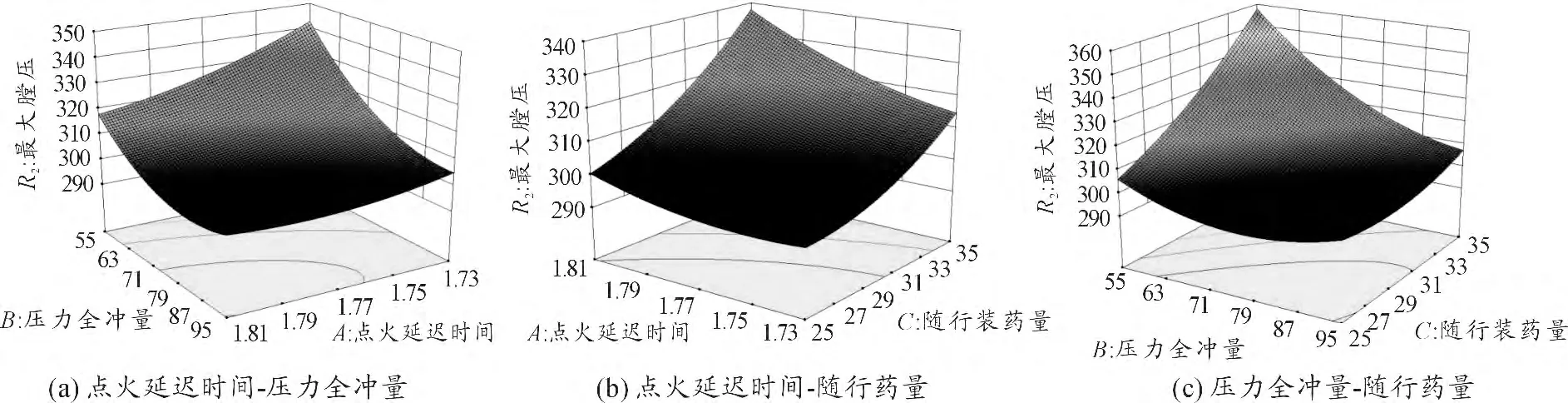
圖8 最大膛壓的響應面方程的等值曲面圖
3 結論
1)點火延遲時間、隨行藥壓力全沖量和隨行藥量對隨行裝藥結構的彈丸初速均有顯著的影響,按影響大小的排序為:隨行藥量>隨行藥壓力全沖量>點火延遲時間。3 種因素間的交互作用對彈丸初速的影響不大。
2)點火延遲時間、隨行藥壓力全沖量和隨行藥量對隨行裝藥結構的最大膛壓均有較大影響,按影響大小的排序為:隨行藥壓力全沖量>隨行藥量>點火延遲時間。3 種因素間的交互作用對最大膛壓影響顯著。
3)利用響應面分析可以求得隨行裝藥結構參數的局部最優解,對裝藥設計具有較好的指導意義。
[1]金志明.高速推進內彈道學[M].北京:國防工業出版社,2001:286.
[2]王浩.隨行裝藥火炮經典內彈道模型與實驗技術研究[J].兵工學報,1996,17(40):298-302.
[3]楊京廣固體隨行裝藥內彈道實驗及數值計算[D].南京:南京理工大學,2006.
[4]王浩隨行裝藥效果與敏感性研究[J].彈道學報,1996,8(1):20-25.
[5]MONTGOMERY D C. Design and analysis of experiments[M].3rd ed.New york:wiley,1991.
[6]戴啟洲,周明華,雷樂成.響應面法優化濕式氧化處理陽離子紅X-GRL 廢水[J].浙江大學學報:工學版,2006,40(11):1889-1894.
[7]楊京廣,余永剛.固體隨行裝藥內彈道模型及數值模擬[J].火炮發射與控制學報,2006(2):1-5.
[8]熊曉莉,黃誠,耿嘎,等. 乙醇對硝酸錳熱分解的影響[J].重慶工商大學學報:自然科學版,2014,31(2):70-73.
[9]何為,薛衛東,唐斌. 優化試驗設計方法及數值分析[M].北京:化學工業出版社,2012:310.
[10]崔軍,趙海龍,皇才進.基于發射裝藥技術提高穿甲彈初速研究[J].四川兵工學報,2014(5):4-6.

