三軸矢量數據融合的視覺跟蹤慣性穩定系統設計
江瀟,何波賢,鄭鐵山,岳明
(92724部隊,青島266108)
引 言
在三軸視覺跟蹤慣性穩定控制系統中,保持視覺穩定的關鍵技術在于隔離因外界因素引起的抖動。慣性穩定系統的核心是檢測角運動敏感器件三軸陀螺,對轉臺姿態擾動十分敏感,一旦發生擾動立刻反饋到控制系統[1]。在實際系統的測量中,由于三軸陀螺本身存在零點漂移誤差以及隨機誤差,采用多傳感器信息融合技術處理慣性穩定姿態信號,把三軸陀螺、加速度計、磁極三個不相干的三維矢量進行互補融合,致力提高慣性穩定系統測量精度[2]。
1 系統框架設計
三軸視覺跟蹤穩定平臺的姿態測量系統主要由三軸陀螺、三軸加速度計、三軸磁計、溫度傳感器和STM32系列微處理器組成。MPU-6050集成了三軸陀螺、三軸加速度計、溫度傳感器,HMC5883是三軸磁阻傳感器。姿態測量系統框架結構如圖1所示。
2 基于四元數卡爾曼濾波器設計
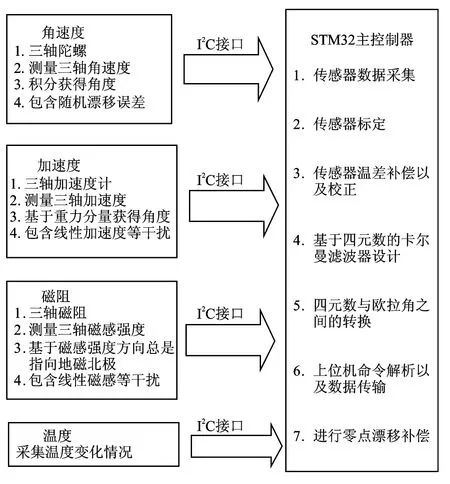
圖1 姿態測量系統框架結構
三軸陀螺的主要測量載體是三維角速度,三軸加速度計的主要測量載體三維重力加速度,三軸磁計用來測量三維地磁強度。其中三軸加速計和三軸磁阻傳感器提供了兩個不相關的三維矢量,并且這些矢量可以作為觀測矩陣來校正因為三軸陀螺引起的誤差[3]。四元數卡爾曼濾波器結合這三種傳感器的特點,進行數據互補融合,以三軸陀螺輸出的角速度為狀態更新,以重力加速度和磁場強度作為觀測方程的更新,估計出精度高、穩定性強的姿態角[4]。
2.1 狀態量隨時間更新矩陣
基于四元數的卡爾曼濾波器是以四元數為狀態量,所以設狀態參數為:
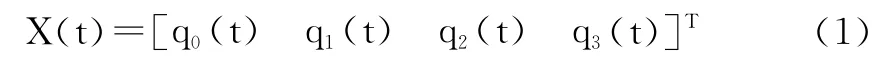
卡爾曼濾波器狀態方程是基于三軸陀螺四元數輸出進行設計,建立四元數的狀態方程為四元數的微分方程:
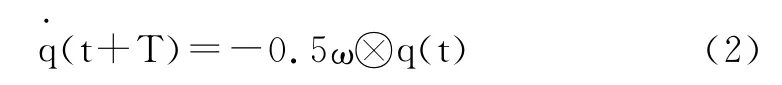
采用基于定時采樣的畢卡三階逼近法將此四元數微分方程展開,已知四元數的畢卡三階逼近法形式為:
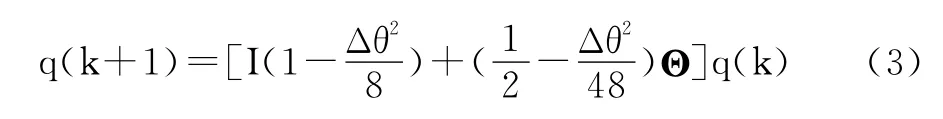
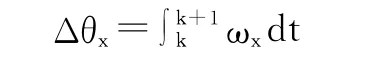
Δθy、Δθz同理可求,其中:Δθx、Δθy、Δθz為 三 軸 陀 螺 在[k,k+1]采樣時間內的角增量。
基于四元數的微分方程矩陣形式為:
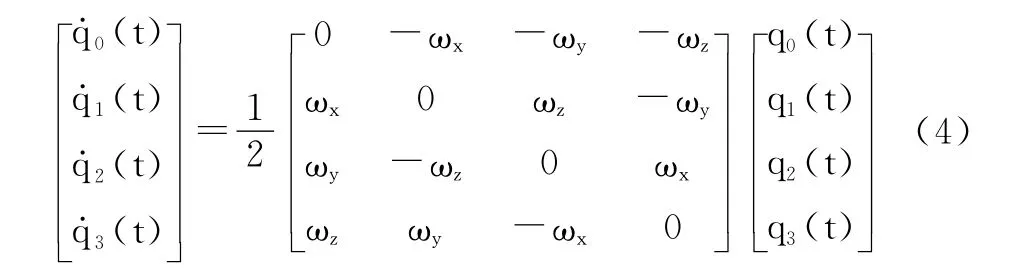
將式(3)代入四元數的微分方程矩陣,得到狀態變量隨時間更新的矩陣為:
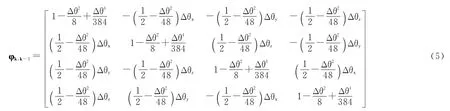
2.2 觀測方程更新
把三軸加速度計以及三軸磁計作為卡爾曼濾波器觀測方程的輸入,那么觀測方程的更新就是基于加速度計和磁計數據的更新,也就是把三軸加速度計和三軸磁計的本體坐標系上的重力加速度和地磁場的參考矢量,通過四元數轉移矩陣轉移到當前坐標系上進行處理。其中四元數轉移矩陣為[5]:
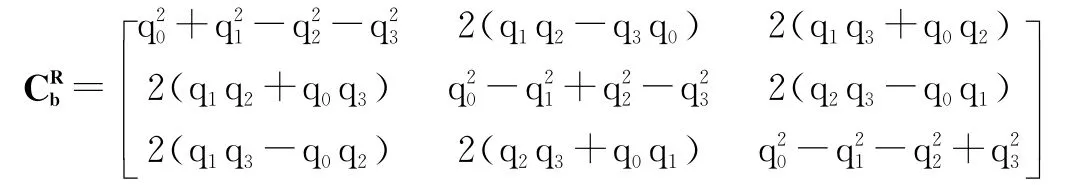
假設三維參考向量V=[VxVyVz]轉移到旋轉當前坐標系中可由觀測方程表示:

由于上式是非線性方程,所以對h進行求取雅可比矩陣,也就是h對X偏導的雅可比矩陣:
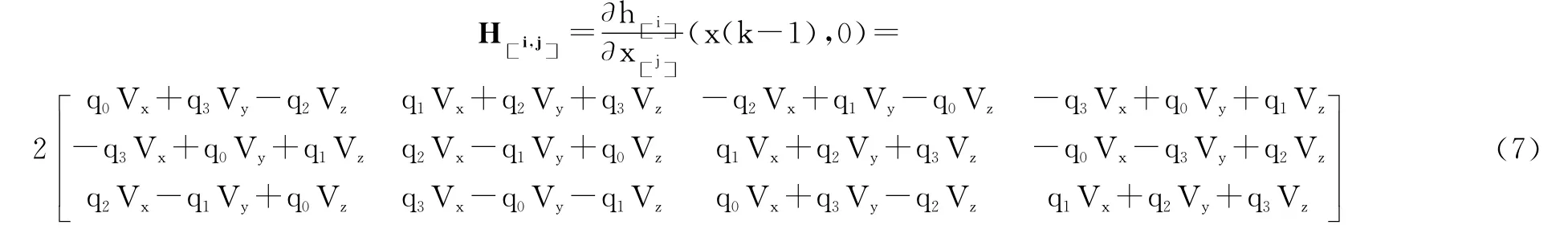
當重力加速度(相對加速度靜止水平放置時)觀測更新時有:
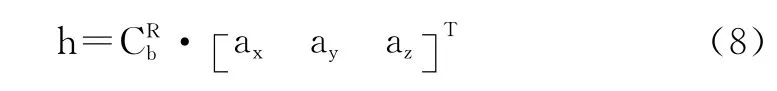
當磁場觀測(相對磁阻傳感器靜止水平放置并航向指向正北時)更新時有:
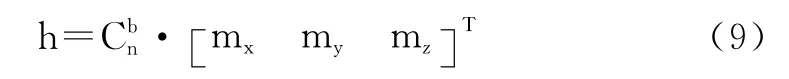
把式(8)、式(9)代入式(7),得到基于三軸加速度計以及三軸磁計的觀測方程:
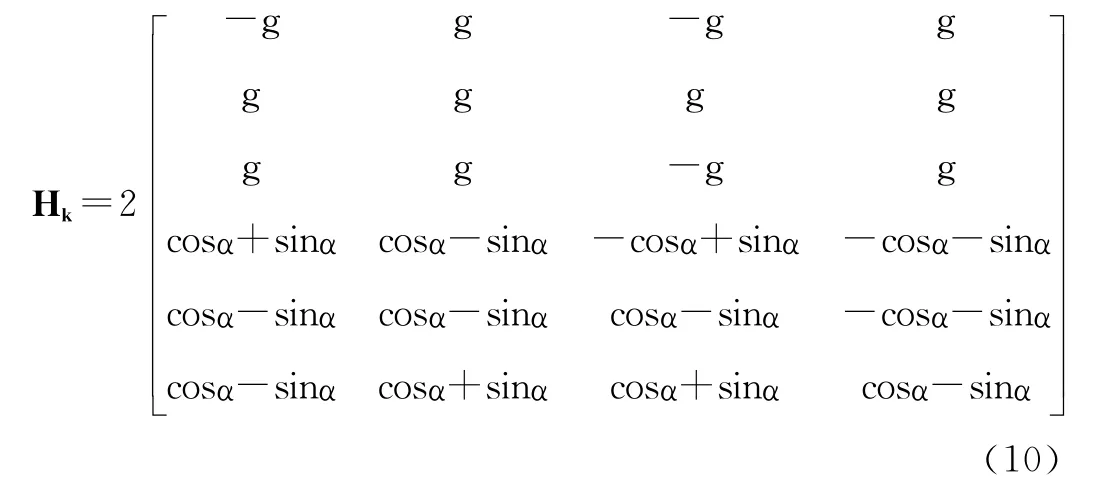
式中:α為磁傾角。
2.3 定姿算法
觀測方程進行了離散線性化處理后,得到了狀態更新的方程,并且系統的過程噪音Wk-1和系統的量測噪聲Vk滿足上述的要求,則卡爾曼濾波方程滿足以下求解過程。
預測狀態:
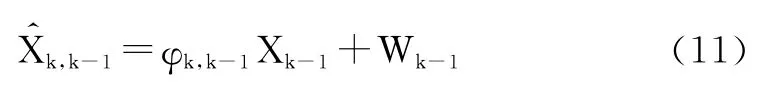
狀態估計:
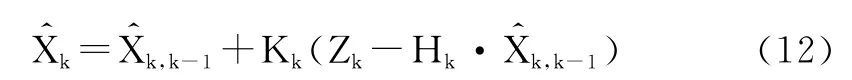
由于式(12)并不是離散的,必須采用以下離散連續的公式進行代替:
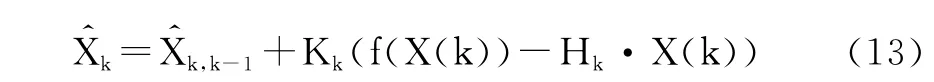
用陀螺或者加速度計以及磁計來計算姿態角,陀螺的特性就是動態性能比較好,但是較長時間內存在零點漂移,使誤差結果放大;而加速度計以及磁計靜態性能較好,但是運動時就會引起較大的噪音,既不能全依靠陀螺計算的值,也不可以完全依靠加速度計和磁計計算出來的數值,只能利用傳感器的互補信息進行相互補償,用陀螺計算出來的姿態角,以及加速度計和磁計計算出來的姿態角進行作差,所以f(X(k))就是加速計和磁計計算出來的角度,也就是三軸加速度計和磁計測量出來的數值。HkX(k)就是陀螺在上一次誤差四元數計算出來的歐拉角。
濾波增益:
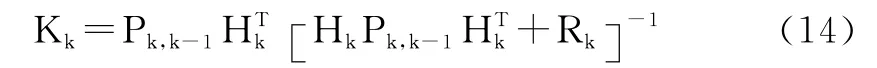
預測誤差方差陣:
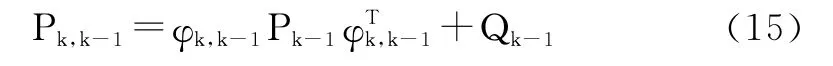
估計誤差協方差:
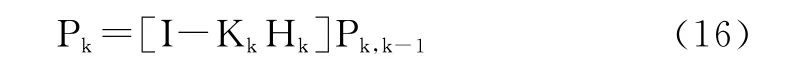
卡爾曼濾波是一種遞推的過程,該算法充分利用陀螺輸出的角速度信號以及加速度計、磁計信號互補特性[6]。當運動時,以陀螺的動態特性為主;靜止時,以加速度計、磁計的靜態特性為主。權衡參數主要由增益矩陣決定,得到對狀態輸出的最優估計,增益矩陣的特性主要依據當前更新估計以及前次狀態系統估計的統計特性得到,減小了系統計算量。
3 程序設計
基于四元數卡爾曼濾波器設計的三軸視覺跟蹤慣性穩定系統程序流程。主要的處理步驟如下:
①系統的初始化主要包括主控STM32、傳感器MPU6050、HMC5883初始化。
②首先在三軸慣性系統保持靜止時,通過采集3 200組數據進行零位自動標定,同時完成卡爾曼濾波器誤差協方差矩陣P、噪聲協方差矩陣Q、方差強度矩陣R的初始化;然后通過采集三軸加速度以及三軸磁場強度計算出系統的初始姿態;再把東—北—天坐標系下的磁場強度初始化;最后,把歐拉角形式的初始化姿態轉化成四元數形式,實現四元數卡爾曼濾波器的初始化。
③采集三軸陀螺10個數據,取平均值,然后對四元數的卡爾曼濾波器隨時間預測更新;然后采集三軸加速度以及三軸磁場強度的數值,對卡爾曼濾波器的觀測矩陣進行更新。
④當加速度過大時,不是進行數據融合,而是進行誤差協方差矩陣P更新;當判斷加速度在合適的范圍時,進行卡爾曼數據融合。
⑤完成卡爾曼更新后,通過UD分解確保誤差協方差P不發散,最后把四元數轉換成歐拉角形式。
程序流程如圖2所示。
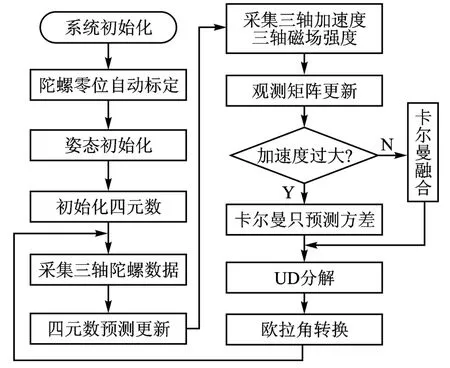
圖2 程序流程圖
4 對比實驗
為了檢測這種算法輸出的姿態精度,利用一款工業級的微垂直陀螺系統進行對比實驗。微垂直陀螺系統是一款高性能陀螺系統,基于三軸陀螺儀和三軸加速度計設計的,采用自適應卡爾曼數據融合算法,以100 Hz更新速率輸出載體的慣性運動信息(三軸角速度、三軸加速度)、最優姿態角(橫滾角和俯仰角)和溫度等參數,并對傳感器的安裝誤差、軸間正交誤差和溫度誤差進行有效補償。
實驗主要采用三軸搖擺臺進行測試,首先把陀螺系統安裝在三軸搖擺臺的內框上,如圖3所示,然后對轉臺進行轉動,通過轉臺上的1024光柵碼盤計算出轉臺轉過的角度并傳遞到上位機,上位機同時采集陀螺和碼盤的數據進行對比。

圖3 三軸搖擺臺
本實驗主要采用俯仰角的數據進行對比。圖4為微垂直陀螺系統輸出的俯仰角以及碼盤輸出的角度,它的優點就是跟蹤性能比較好,但是波峰相差比較大,最大的幅度差在20°左右,主要原因就是自適應卡爾曼濾波器的參數沒有進行優化,把波形的高通部分當作噪音來處理,所以該類型的陀螺系統性能并不是很好,存在很多改進的可能。
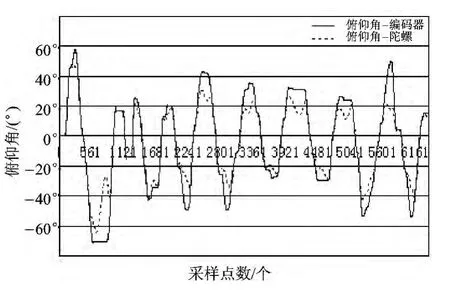
圖4 微垂直陀螺數據
由圖5可知,基于四元數卡爾曼濾波器設計的三軸陀螺系統的性能更具有優勢,角度誤差在±2°范圍,還增加了三軸磁計融合陀螺方位角信息,可滿足三軸跟蹤轉臺全方位測量要求。
結 語
采用四元數擴展卡爾曼濾波算法把三軸陀螺、加速度、磁阻傳感器的誤差特性進行相互擬合、相互補償,不僅提高了姿態解算的精度,而且更新速率快、實時性強。目前,該測試系統已用于視覺目標跟蹤系統進行測試,滿足了三軸視覺跟蹤穩定系統對姿態控制測量的需求。

圖5 陀螺數據
[1]辛哲奎,方勇純,張雪波.小型無人機地面目標跟蹤系統機載云臺自適應跟蹤控制[J].控制理論與應用,2010,27(8):1002-1003.
[2]呂漫麗,孫靈芳.多傳感器信息融合技術[J].自動化技術與應用,2008,2(2):79-80.
[3]秦永元.慣性導航[M].2版.北京:科學出版社,2014.
[4]秦永元,張洪鉞,汪叔華.卡爾曼濾波與組合導航原理[M].2版.西安:西北工業大學出版社,2012.
[5]徐梓皓,周召發,孫立江.基于卡爾曼濾波器的姿態角測量系統設計[J].電子測量技術,2014,37(1):1-2.
[6]RuanJianS-guo,LinJiaS-jun.Analysis on stability of digital protectional gorithms[J].Proceedings of 2005 IEEE International conference on information acquisition,2005:313-317.

