基于局部熵的量子衍生醫(yī)學(xué)超聲圖像去斑
付曉薇代 蕓 陳 黎 田 菁 丁 勝
(武漢科技大學(xué)計算機科學(xué)與技術(shù)學(xué)院 武漢 430065)
(智能信息處理與實時工業(yè)系統(tǒng)湖北省重點實驗室 武漢 430065)
基于局部熵的量子衍生醫(yī)學(xué)超聲圖像去斑
付曉薇*代 蕓 陳 黎 田 菁 丁 勝
(武漢科技大學(xué)計算機科學(xué)與技術(shù)學(xué)院 武漢 430065)
(智能信息處理與實時工業(yè)系統(tǒng)湖北省重點實驗室 武漢 430065)
針對現(xiàn)有醫(yī)學(xué)超聲圖像去斑方法的不足,該文提出一種基于局部熵的量子衍生醫(yī)學(xué)超聲圖像去斑新方法。首先,將對數(shù)變換后的圖像進(jìn)行雙樹復(fù)小波變換(DTCWT),并對信號與噪聲分別建模;然后,提取復(fù)小波中子代與父代小波系數(shù)的實部,計算其局部熵并進(jìn)行歸一化乘積,結(jié)合量子衍生理論得到用來調(diào)整信號與噪聲出現(xiàn)概率的可調(diào)參數(shù);最后,利用改進(jìn)的雙變量收縮函數(shù)獲得去斑后的圖像。通過實驗,結(jié)果表明該方法與已有方法相比能夠更有效地濾除醫(yī)學(xué)超聲圖像中的斑點噪聲并保留細(xì)節(jié)信息。
圖像處理;局部熵;量子衍生;雙樹復(fù)小波變換;雙變量收縮
1 引言
由于超聲圖像成像過程中超聲信號在體內(nèi)的散射,圖像會產(chǎn)生特有的斑點噪聲,降低了超聲圖像的質(zhì)量。如何有效去除斑點噪聲,增強醫(yī)學(xué)超聲圖像質(zhì)量和臨床應(yīng)用性的研究具有重要意義。
早期的去斑方法研究主要采用線性濾波器進(jìn)行斑點抑制[1,2],這類方法能去除一定的斑點噪聲,但圖像細(xì)節(jié)信息易丟失。為了克服此缺陷,又提出了自適應(yīng)加權(quán)中值濾波[3]和最大后驗概率(Maximum A Posteriori, MAP)[4]估計等方法,但仍然存在圖像對比度降低,邊界易模糊等現(xiàn)象。過去幾年,人們提出大量去斑方法。文獻(xiàn)[5]提出斑點噪聲抑制各向異性擴散濾波器(Speckle Reducing Anisotropic Diffusion, SRAD),此濾波器性能優(yōu)于傳統(tǒng)濾波器,能有效去斑的同時保護(hù)圖像邊緣細(xì)節(jié),但該算法實現(xiàn)迭代次數(shù)多、運行時間過長,SRAD模型受尺度函數(shù)影響較大。文獻(xiàn)[6]提出非局部平均(Non-Local Means, NLM)去噪算法,基本思想是通過計算圖像像素點與其周圍整個區(qū)域的灰度相似性進(jìn)行加權(quán)平均。該方法能保持一定的圖像細(xì)節(jié)、紋理等特征,但仍存在邊緣區(qū)域去斑效果較差的現(xiàn)象。在傅里葉變換中,同態(tài)維納濾波是一種經(jīng)典去斑方法[7]。隨著小波工具的發(fā)展,文獻(xiàn)[8]提出一種基于小波域的經(jīng)典去斑Genlik方法,其主要通過選取優(yōu)化參數(shù)將貝葉斯理論用于小波域去斑。該方法可獲得一定的去斑效果,但抑斑能力有限。文獻(xiàn)[9]提出一種新的非參數(shù)統(tǒng)計模型。首先,采用蟻群算法對整幅圖像參數(shù)尋優(yōu),然后利用統(tǒng)計模型有效濾除乘性斑點噪聲。但該方法時間復(fù)雜度較高,如何快速尋找最優(yōu)化參數(shù)仍有待研究。文獻(xiàn)[10]提出一種基于雙變量收縮函數(shù)的雙樹復(fù)小波(Dual-Tree Complex Wavelet Transform, DTCWT)去噪方法(BIvariate DTCWT, BIDTCWT),能有效濾除加性噪聲。文獻(xiàn)[11]將BIDTCWT用于醫(yī)學(xué)超聲圖像去斑中,但該方法噪聲與信號的模型單一,去斑效果不夠穩(wěn)定。為此,本文將結(jié)合參數(shù)統(tǒng)計模型估計噪聲與信號的方差,并利用DTCWT多方向選擇性的優(yōu)勢對圖像進(jìn)行小波變換。
2001年,量子信號處理(Quantum Signal Processing, QSP)被首次提出[12]。文獻(xiàn)[13]研究信號處理基本流程,利用量子態(tài)疊加原理和坍縮測量機制,開發(fā)了基于量子衍生的信號處理技術(shù)。受相關(guān)文獻(xiàn)[14]啟發(fā),文獻(xiàn)[15]首次將量子衍生理論用于醫(yī)學(xué)超聲圖像去斑中。該去斑方法根據(jù)醫(yī)學(xué)圖像小波分解系數(shù)的特點,借鑒量子衍生相關(guān)理論,提出用來調(diào)整信號與噪聲出現(xiàn)概率的量子衍生參數(shù)。該方法取得了一定的去斑效果,但參數(shù)估計僅考慮第2層小波全局高頻系數(shù)的分布特征,其自適應(yīng)去斑能力仍有待改進(jìn)。
在文獻(xiàn)[15]的基礎(chǔ)上,本文結(jié)合局部熵理論的特點,提出一種新的基于局部熵的量子衍生醫(yī)學(xué)超聲圖像去斑方法。該方法充分顯示了DTCWT更好的方向選擇性、平移不變性等優(yōu)點,并針對圖像局部所含信息量的差異進(jìn)行斑點抑制,可取得令人滿意的去斑效果。
2 基于DTCWT的斑點噪聲抑制
2.1 信號與斑點噪聲建模
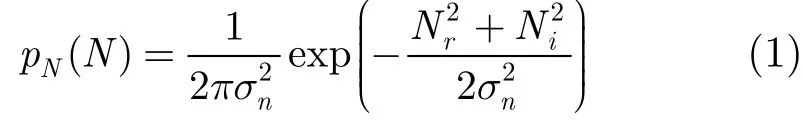
由于不同超聲圖像具有不同的信號概率,只利用單一模型對信號建模的方式不具備通用性。因此,本文采用文獻(xiàn)[15]提出的帶可調(diào)參數(shù)的信號模型對超聲圖像信號建模。
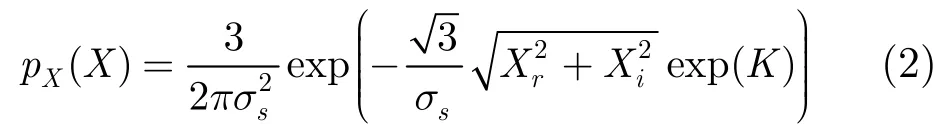
式(2)中,sσ為信號的標(biāo)準(zhǔn)差,K為可調(diào)參數(shù)。文獻(xiàn)[15] 中參數(shù)K是通過最小化擬合曲線確定,其誤差精度決定了去斑的程度。而本文方法根據(jù)局部熵與量子衍生的相關(guān)特性來確定參數(shù)K,其適應(yīng)性更強。
2.2 貝葉斯MAP估計器
經(jīng)DTCWT處理后的超聲圖像小波系數(shù)具有非高斯特性,式(3)中1x,2x分別表示在同一位置子代、父代的小波系數(shù),從而有

y1和y2是含斑圖像,x1和x2是相對無噪圖像,n1和n2是斑點噪聲。式(3)可以寫為y=x+n,其中x=(x1,x2), n=(n1,n2), y=(y1,y2)。本文采用貝葉斯最大后驗概率(Maximum A Postoriori, MAP)對信號進(jìn)行估計。在含斑圖像y已知以及條件概率密度函數(shù)|xyp取最大值的條件下,求出其對應(yīng)信號的估計值,表達(dá)式為
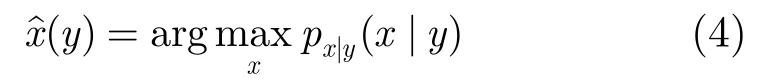
根據(jù)貝葉斯原理,利用所提出的信號模型,結(jié)合式(1)和式(2),得到本文改進(jìn)后的雙變量收縮函數(shù),也稱MAP估計器,其定義為
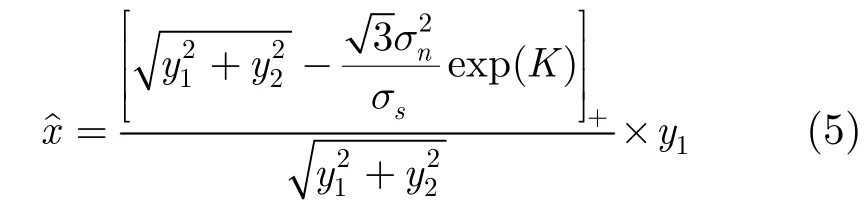
其中,K為可調(diào)參數(shù)。當(dāng)參數(shù)0K=時,式(5)為傳統(tǒng)的雙變量濾波器。
3 基于局部熵的量子衍生參數(shù)K的選取
局部熵可以反映圖像某一區(qū)域所含信息量的多少。對于圖像中任意一點(,)ij,選取局部MN×窗口,定義局部熵為
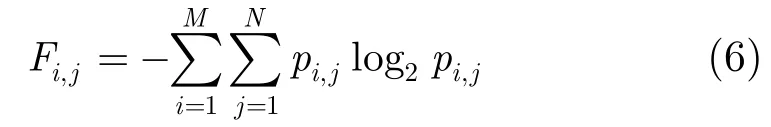
其中,ijp為圖像中像素在(,)ij處的概率,通過實驗分析,本文選取9×9窗口計算其局部熵。在圖像中,假如某一區(qū)域含有的信息量越多,則圖像對比度越好,能更好地突出細(xì)節(jié)部分;反之,圖像灰度變化沒那么劇烈,對比度越差[17,18]。因此,在圖像灰度較平坦的區(qū)域,局部熵值比較小;而在圖像邊緣處,灰度變化劇烈,熵值也較大。
根據(jù)小波系數(shù)之間的相關(guān)性,如果父代系數(shù)具有較大的模,則其子代系數(shù)也具有較大的模[15]。本文考慮其相關(guān)性,結(jié)合局部熵理論,考慮到如果父代系數(shù)實部的局部熵較大時,局部含有的信息量也越大,則其對應(yīng)的子代系數(shù)實部同樣具有較大的局部熵,而父子代相關(guān)性也越大。小波系數(shù)與其父系數(shù)實部局部熵的乘積表達(dá)式為
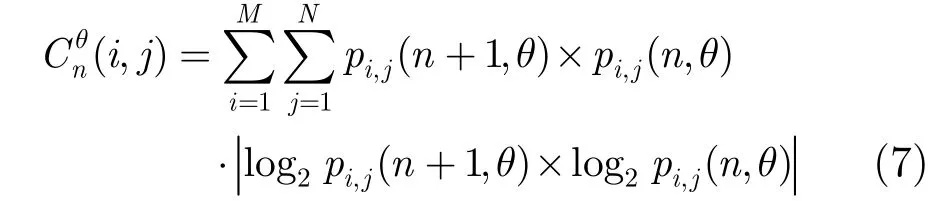
其中,θ為子帶的6個方向:±15°, ±45°, ±75°,pi,j(n,θ)和pi,j(n+1,θ)分別為圖像中方向為θ的小波系數(shù)與其父代系數(shù)在(i,j)處灰度值的概率。
含斑圖像主要由信號與斑點噪聲組成,而在量子疊加態(tài)原理中,有|0>與|1>兩種量子基態(tài)。因此本文聯(lián)想到將|看作是噪聲與信號的疊加,即
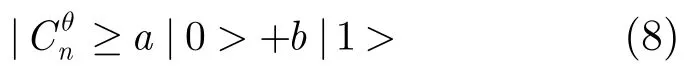
其中a, b分別表示量子基態(tài)|0>與|1>的概率幅。|a|2表示噪聲狀態(tài)|0>對應(yīng)的測量概率,|b|2表示信號狀態(tài)|1>對應(yīng)的測量概率。將(i,j)歸一化:
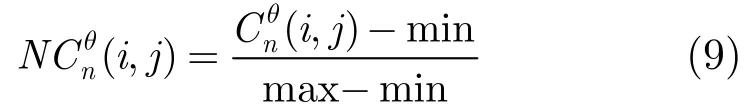
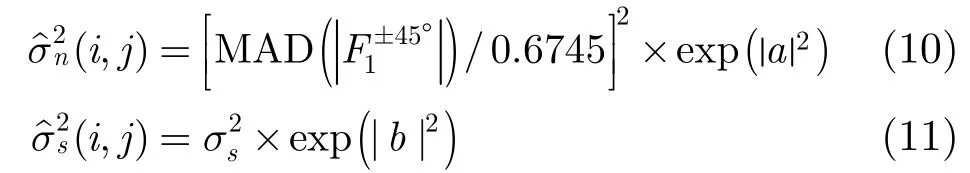

將K代入式(5)可知,如果信號出現(xiàn)概率越小,則相對噪聲出現(xiàn)概率越大,其對應(yīng)收縮因子變小。本文根據(jù)圖像局部熵的大小自適應(yīng)調(diào)整噪聲與信號出現(xiàn)的概率,得到用來控制雙變量收縮函數(shù)的收縮因子。通過大量實驗圖片測試,本文所提出的自適應(yīng)收縮因子不僅可有效控制斑點噪聲,而且有利于邊緣細(xì)節(jié)的保持。
4 本文去斑方法
根據(jù)本文提出的方法,醫(yī)學(xué)超聲圖像去斑流程如圖1所示。首先,輸入圖像,對其進(jìn)行對數(shù)變換后得到圖像Y;再利用DTCWT對圖像Y進(jìn)行小波分解,并分別對噪聲與信號建模;然后,本文利用式(7)計算復(fù)小波系數(shù)與其父系數(shù)實部局部熵的乘積,并歸一化為(i,j);根據(jù)量子衍生特性,結(jié)合(i,j),分別得到噪聲方差和信號方差的估計式;并利用帶可調(diào)參數(shù)的雙變量收縮函數(shù)式(5),得到去斑后的小波系數(shù);最后,對去斑后子帶系數(shù)進(jìn)行DTCWT逆變換、指數(shù)變換得到去斑后圖像。
5 實驗結(jié)果
為了驗證所提出方法的性能,將本文方法用于模擬斑點超聲圖像和真實斑點超聲圖像的斑噪去除中,并與現(xiàn)有經(jīng)典方法:維納濾波[7],BIDTCWT[10], Genlik[8],文獻(xiàn)[9]和文獻(xiàn)[15]方法進(jìn)行對比實驗。對圖像進(jìn)行處理前,先對其進(jìn)行對數(shù)變換。其中維納濾波采用55×窗口;Genlik方法設(shè)置窗口大小為55×,可調(diào)參數(shù)為3。本文在2.90 GHz英特爾奔騰雙核CPU G2020計算機上利用MATLAB R2012b編程工具進(jìn)行實驗。
為了實現(xiàn)客觀評價,本文采用如下3種評價指標(biāo)[15]:噪聲信噪比 (SNR),邊緣保持度(β)[19]和等效視數(shù)(Equivalent Number of Looks, ENL)。一般而言,SNR的值越大,圖像中的噪聲越小。β取值0到1之間,如果值越接近1,則表明圖像邊緣保持的越好。等效視數(shù)指標(biāo)則反映的是圖像所選同質(zhì)區(qū)域的平滑程度,等效視數(shù)越大,圖像平滑程度越高,抑斑能力越強。

圖1 本文去斑方法流程
5.1 模擬斑點超聲圖像實驗
本文利用http://telin.ugent.be/~sanja/提供的程序SimulateSpeckle.m模擬生成斑點噪聲。模擬實驗測試了大量圖像,文中列出2幅具有代表性圖像的視覺效果比較。圖2和圖3分別給出標(biāo)準(zhǔn)差為0.9的模擬斑點超聲肝臟圖像和Al圖像經(jīng)本文方法與傳統(tǒng)去斑方法處理后的視覺效果。
圖2中,BIDTCWT、文獻(xiàn)[9]方法較維納濾波方法雖然能更好的保持圖像邊緣細(xì)節(jié),但是去斑能力不強,其中超聲肝臟圖像殘留較多的斑點噪聲;而Genlik方法雖然可以對斑點噪聲進(jìn)行很好的平滑,但是圖像邊緣細(xì)節(jié)保持能力較弱,圖像易模糊;本文方法較其他方法在有效去斑的同時也獲得了較大的邊緣保持度。在圖3中,由于Al圖像邊緣細(xì)節(jié)較少,本文方法抑斑效果最顯著。
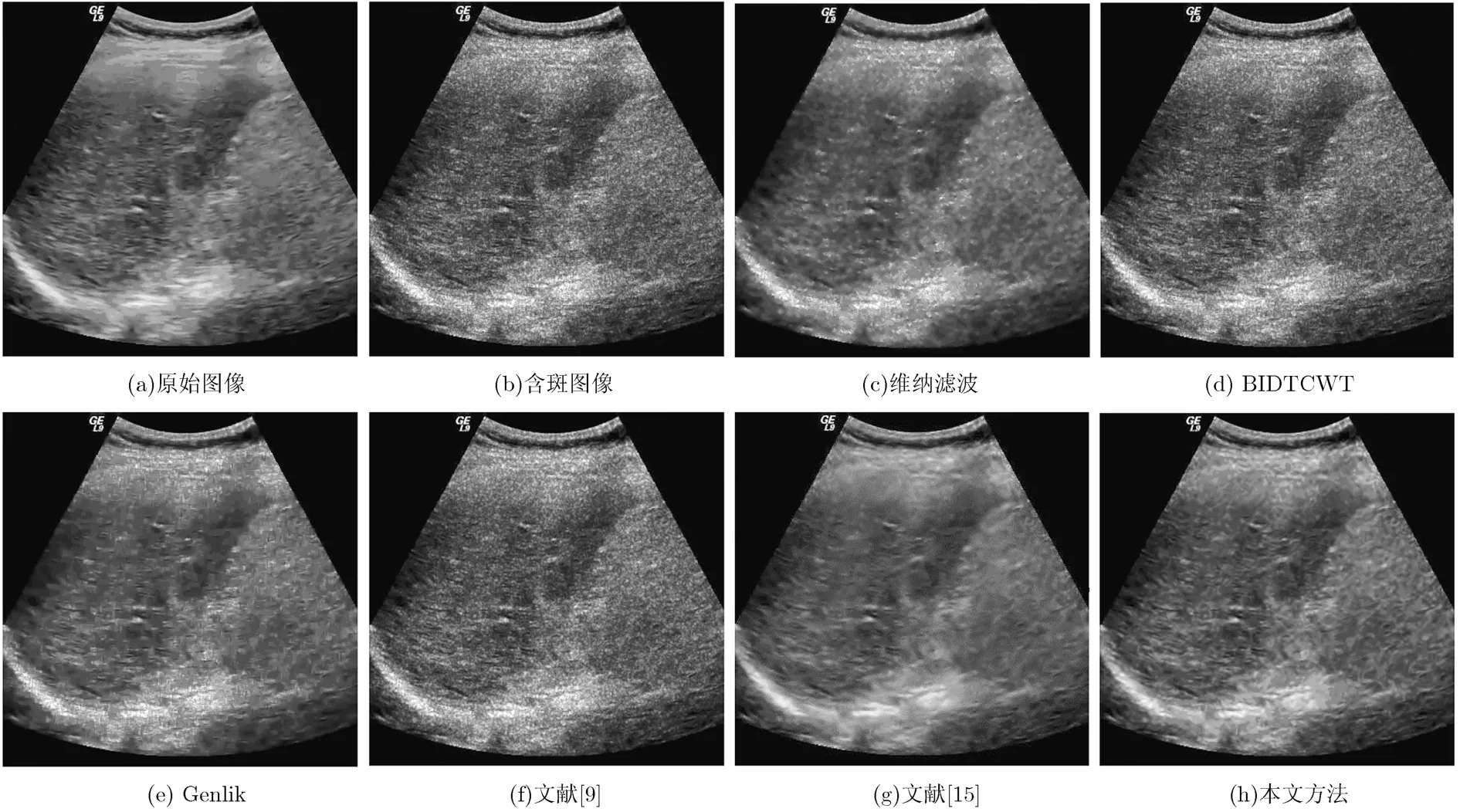
圖2 超聲肝臟圖像不同方法實驗結(jié)果
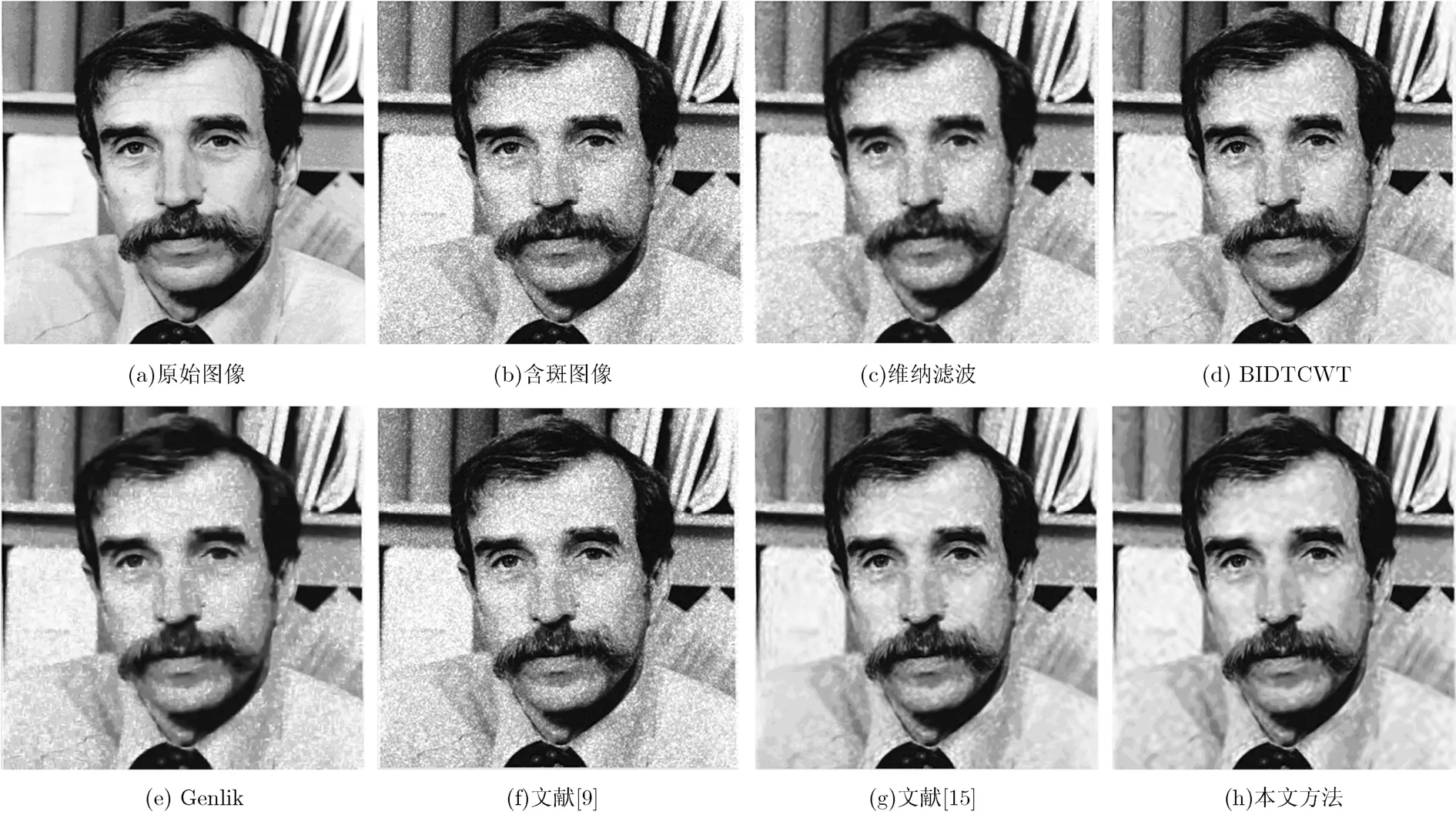
圖3 Al圖像不同方法實驗結(jié)果
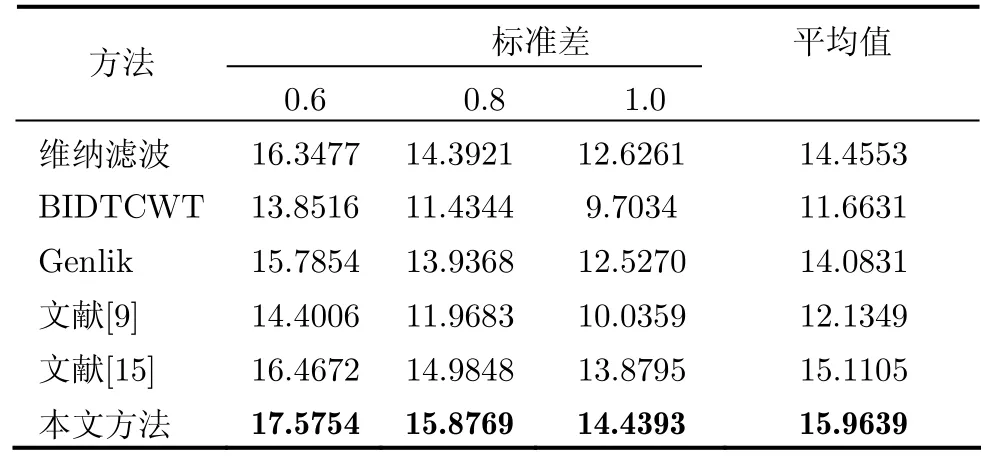
表1 相關(guān)方法對模擬斑點超聲肝臟圖像的SNR(dB)比較
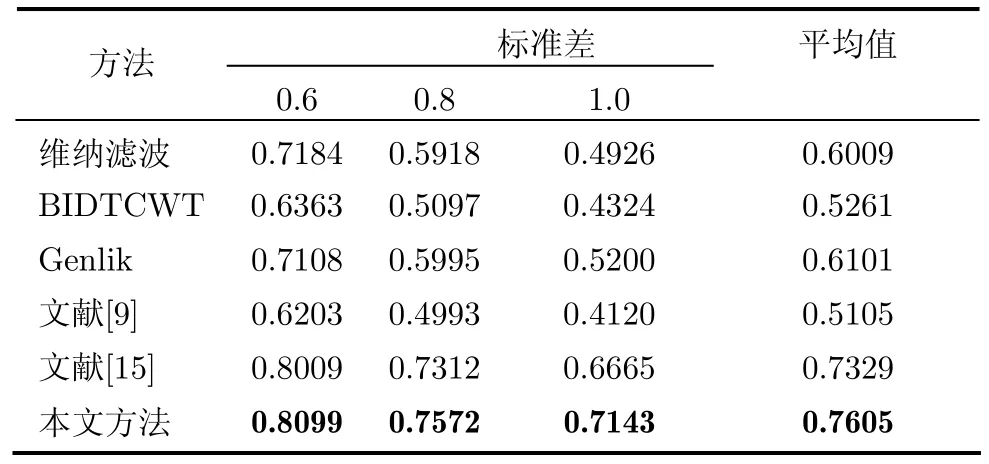
表2 相關(guān)方法對模擬斑點超聲肝臟圖像的β比較
為了驗證本文方法的去斑性能,表1、表2分別列出含模擬斑點噪聲標(biāo)準(zhǔn)差為0.6, 0.8, 1.0的超聲肝臟圖像經(jīng)本文方法及傳統(tǒng)去斑方法處理后的SNR值和β值。此外,結(jié)合文獻(xiàn)[9]的性能評價方式,本文統(tǒng)計出不同方法的SNR和β的平均值進(jìn)行對比分析。
圖4給出了模擬斑點標(biāo)準(zhǔn)差為0.5~1.0的6幅含斑圖像經(jīng)不同方法處理后獲得的去斑圖像SNR曲線圖。圖4(a)對應(yīng)原始圖像為超聲肝臟圖像(圖2(a))的實驗曲線,圖4(b)對應(yīng)原始圖像為Al圖像(圖3(a))的實驗曲線。
從視覺效果與客觀評價指標(biāo)上分析,實驗結(jié)果表明,對于不同程度的斑點噪聲,本文方法均可獲得較大的SNR值,邊緣保持能力同樣穩(wěn)定,對大多數(shù)圖像具有較強的去斑能力。
5.2 真實斑點超聲圖像實驗
本文采用大小為503×503、含真實斑點的腎臟醫(yī)學(xué)超聲圖像(圖5(a))作對比實驗,比較各種方法的去斑效果。圖5(b)~圖5(h)為原始含斑圖像和不同方法去斑后的局部區(qū)域放大效果圖,其中白色矩形框1和白色矩形框2為所選的同質(zhì)區(qū)域。從圖5中可知,本文方法在主觀視覺上平滑程度最高,抑斑效果最佳。
表3列出對真實超聲圖像進(jìn)行本文相關(guān)方法處理后的性能比較結(jié)果。實驗結(jié)果表明,本文方法去斑后圖像能獲得較大的ENL值,且能有效抑制斑點噪聲。不同去斑方法分別對圖5(a)獨立處理10次,從統(tǒng)計出的平均運行時間可知,本文方法的計算速度雖然較BIDTCWT和文獻(xiàn)[15]略慢。但是,計算復(fù)雜度相比其它方法降低了。相比其他幾種方法,本文方法在提高同質(zhì)區(qū)域平滑性的同時,能較好的保持圖像邊緣,整體更利于實時應(yīng)用。
綜上所述,相比于已有的量子衍生方法[15],本文基于局部熵的量子衍生方法在較好地保持對模擬斑點超聲圖像去斑性能的同時,對真實醫(yī)學(xué)超聲圖像獲得了更明顯的斑噪抑制效果。此外,我們對胎兒和肝臟等醫(yī)學(xué)超聲圖像進(jìn)行本文方法處理,去斑效果同樣顯著,有一定的普適性。
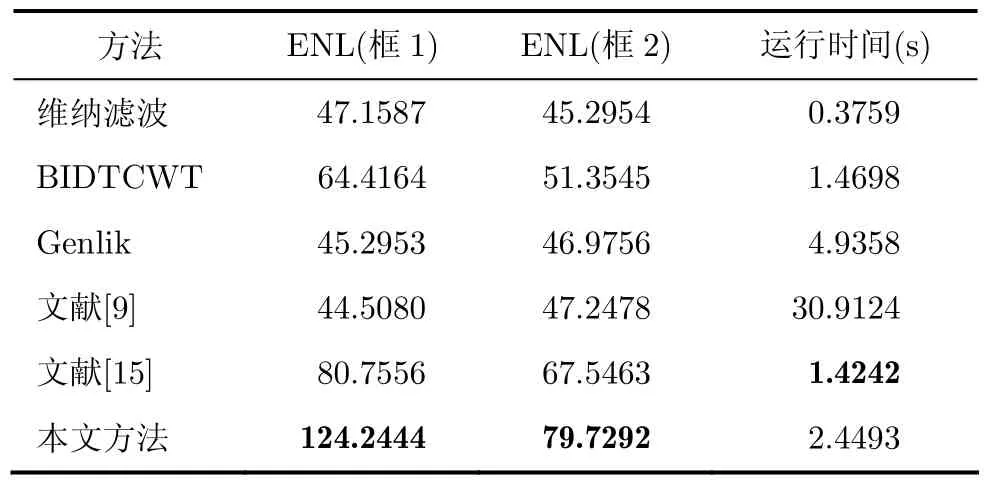
表3 相關(guān)方法對真實超聲圖像的性能比較
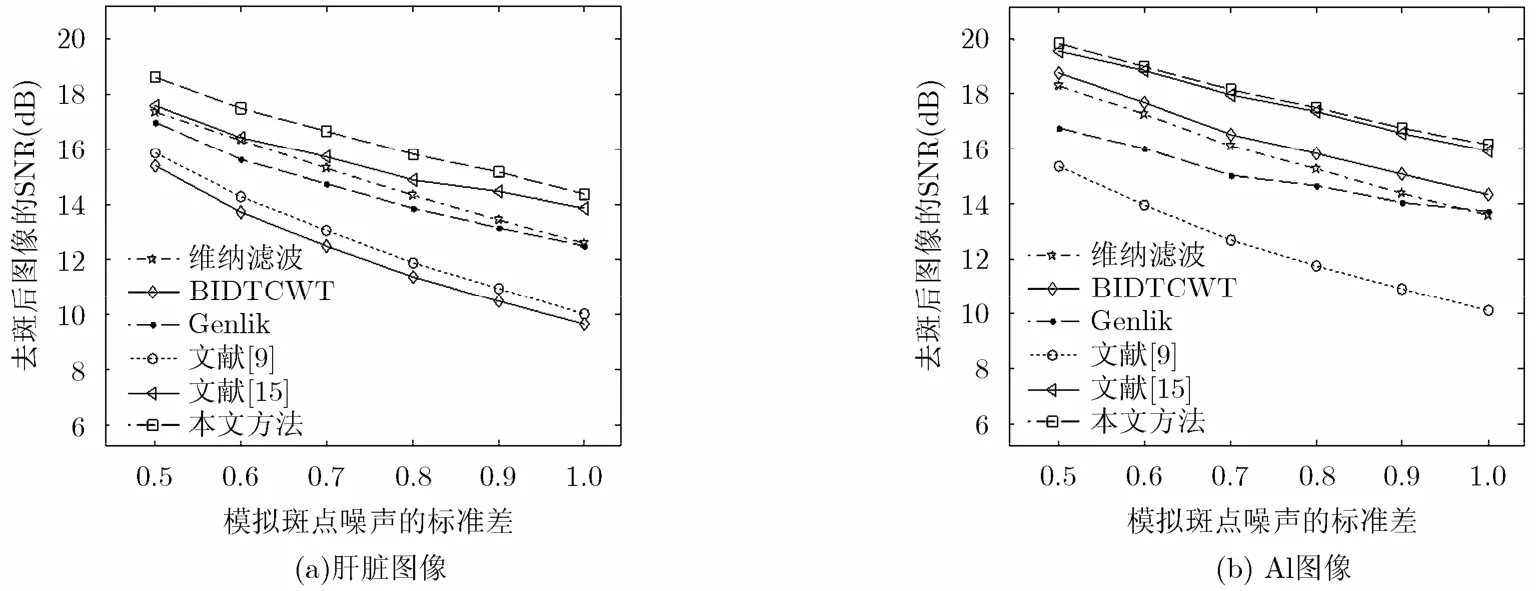
圖4 在不同水平的含斑圖像上,不同方法的信噪比比較
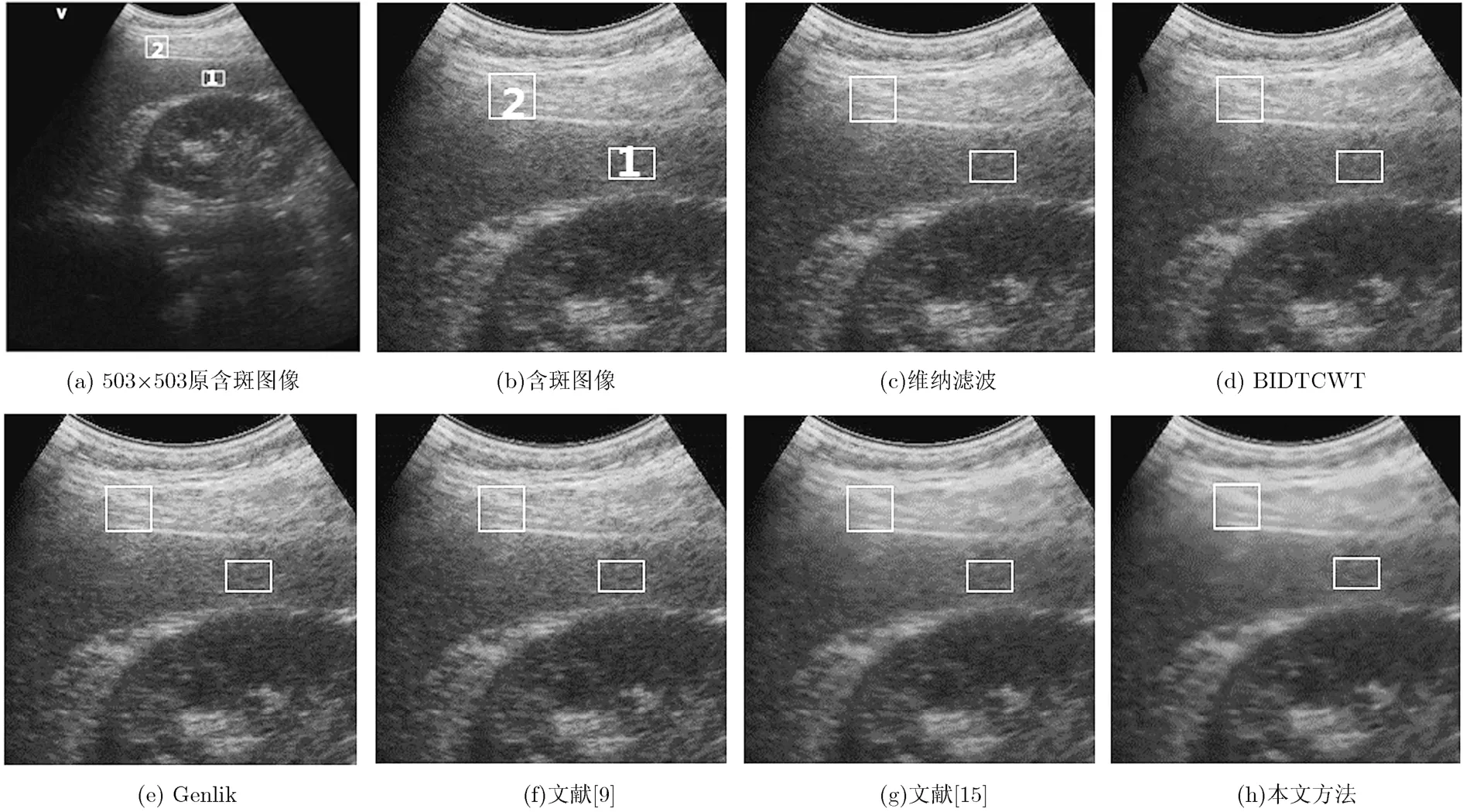
圖5 真實醫(yī)學(xué)超聲圖像不同方法實驗結(jié)果
6 結(jié)束語
本文提出了一種基于局部熵的量子衍生醫(yī)學(xué)超聲圖像去斑新方法。該方法充分考慮了小波系數(shù)的方向選擇性、傳遞性和聚集性,以及DTCWT后斑點噪聲在不同方向子帶的統(tǒng)計特性。針對不同醫(yī)學(xué)圖像局部所含信息量的差異,利用同一位置小波系數(shù)與其父系數(shù)實部局部熵的乘積,結(jié)合量子衍生的相關(guān)特性得到可調(diào)節(jié)圖像噪聲與信號出現(xiàn)概率的可調(diào)參數(shù)。最后,利用此參數(shù)改進(jìn)雙變量收縮函數(shù)抑制斑點噪聲。實驗結(jié)果表明,本文方法在去斑和邊緣保持能力上可獲得較好的效果,能更好地提高真實超聲圖像的去斑性能。該方法為量子理論與圖像處理提供了一種新的有效思路,是一種有效可行的醫(yī)學(xué)超聲圖像去斑方法。
[1] Kuan D T, Sawchuk A, Strand T C, et al.. Adaptive restoration of images with speckle[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(3): 373-383.
[2] Lopes A, Touzi R, and Nezry E. Adaptive speckle filters and scene heterogeneity[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(6): 992-1000.
[3] Loupas T, McDicken W N, and Allan P L. An adaptive weighted median filter for speckle suppression in medical ultrasonic images[J]. IEEE Transactions on Circuits and Systems, 1989, 36(1): 129-135.
[4] Lopes A, Nezry E, Touzi R, et al.. Structure detection and statistical adaptive speckle filtering in SAR images[J]. International Journal of Remote Sensing, 1993, 14(9): 1735-1758.
[5] Yu Y and Acton S T. Speckle reducing anisotropic diffusion[J]. IEEE Transactions on Image Processing, 2002, 11(11): 1260-1270.
[6] Buades A, Coll B, and Morel J M. A non-local algorithm for image denoising[C]. IEEE Computer Society International Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 2005: 60-65.
[7] Solbo S and Eltoft T. Homomorphic wavelet-based statistical despeckling of SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 711-721.
[8] Pizurica A, Philips W, Lemahieu I, et al.. A versatile wavelet domain noise filtration technique for medical imaging[J]. IEEE Transactions on Medical Imaging, 2003, 22(3): 323-331.
[9] Tian J and Chen L. Image despeckling using a non-parametric statistical model of wavelet coefficients[J]. Biomedical Signal Processing and Control, 2011, 6(4): 432-437.
[10] Sendur L and Selesnick I W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency[J]. IEEE Transactions on Signal Processing, 2002, 50(11): 2744-2756.
[11] Kabir S M and Bhuiyan M I H. Speckle noise modeling in the dual-tree complex wavelet domain[C]. International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 2013: 1-6.
[12] Eldar Y C and Oppenheim A V. Quantum signal processing[J]. IEEE Signal Processing Magazine, 2002, 19(6): 12-32.
[13] 謝可夫, 許悟生. 基于量子理論的圖像中值濾波[J]. 計算機工程, 2013, 39(1): 244-247.
Xie Ke-fu and Xu Wu-sheng. Image median filtering based on quantum-theory[J]. Computer Engineering, 2013, 39(1): 244-247.
[14] 張毅, 盧凱, 高穎慧. 量子算法與量子衍生算法[J]. 計算機學(xué)報, 2013, 36(9): 1835-1842.
Zhang Yi, Lu Kai, and Gao Ying-hui. Quantum algorithms and quantum-inspired algorithms[J]. Chinese Journal of Computers, 2013, 36(9): 1835-1842.
[15] 付曉薇, 丁明躍, 蔡超, 等. 基于量子衍生參數(shù)估計的醫(yī)學(xué)超聲圖像去斑算法[J]. 電子學(xué)報, 2011, 39(4): 812-818.
Fu Xiao-wei, Ding Ming-yue, Cai Chao, et al.. Despeckling of medical ultrasound images based on quantum-inspired parameters estimation[J]. Acta Electronica Sinica, 2011, 39(4): 812-818.
[16] Gupta D, Anand R S, and Tyagi B. Despeckling of ultrasound medical images using ripplet domain nonlinear filtering[J]. Signal, Image and Video Processing, 2013, 9: 1-19.
[17] 劉祎, 張權(quán), 桂志國. 基于模糊熵的低劑量 CT 投影降噪算法研究[J]. 電子與信息學(xué)報, 2013, 35(6): 1421-1427.
Liu Yi, Zhang Quan, and Gui Zhi-guo. Noise reduction for low-dose CT sonogram based on fuzzy entropy[J]. Journal of Electronics & Information Technology, 2013, 35(6): 1421-1427.
[18] Azizi S, Samavi S, Mohrekesh M, et al.. Cascaded transform space watermarking based on analysis of local entropy variation[C]. International Conference on Multimedia and Expo Workshops (ICMEW), San Jose, CA, 2013: 1-6.
[19] Wong A and Scharcanski J. Monte Carlo despeckling of transrectal ultrasound images of the prostate[J]. Digital Signal Processing, 2012, 22(5): 768-775.
付曉薇: 女,1977年生,副教授,研究方向為圖像處理、量子信號處理、目標(biāo)識別與跟蹤等.
代 蕓: 女,1989年生,碩士生,研究方向為圖像處理等.
陳 黎: 男,1977年生,副教授,研究方向為圖像處理等.
Quantum-inspired Despeckling of Medical Ultrasound Images Based on Local Entropy
Fu Xiao-wei Dai Yun Chen Li Tian Jing Ding Sheng
(College of Computer Science and Technology, Wuhan University of Science and Technology, Wuhan 430065, China)
(Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System, Wuhan 430065, China)
Aiming at the limitation of existing methods for the medical ultrasound images despeckling, a novel quantum-inspired despeckling method based on the local entropy is proposed for the medical ultrasound images. Firstly, the log-transformed images are decomposed by the Dual-tree Complex Wavelet Transform (DTCWT), and the signal and speckle noise are modeled separately. Then, considering the normalized products of the local entropy of the real components extracted from coefficients and their parents, the adjustable parameter is obtained by the quantum inspired theory to adjust the probability of signal and noise. Finally, the modified bivariate shrinkage function is exploited to obtain the despeckled image. The experimental results show that the proposed method can preserve detail information effectively and reduce the speckle noise of medical ultrasound image at the same time.
Image processing; Local entropy; Quantum inspired; Dual-Tree Complex Wavelet Transform (DTCWT); Bivariate shrinkage
TN911.73
A
1009-5896(2015)03-0560-07
10.11999/JEIT140587
2014-05-06收到,2014-07-31改回
國家自然科學(xué)基金(61201423, 61375017, 61105010)和智能信息處理與實時工業(yè)系統(tǒng)湖北省重點實驗室開放基金子項目(znss2013B016)資助課題
*通信作者:付曉薇 fxw_wh0409@wust.edu.cn

