基于機器視覺檢測的攝像機快速標定與誤差分析
丁婷婷,方 舟,劉 波,張君安
(西安工業大學 機電工程學院,西安 710021)
0 引言
畸變不可避免的存在于通過圖像采集設備獲取的圖像中,如果不對其進行矯正,將會直接影響后續處理的準確性和效率。為了進行矯正,先進行攝像機標定。攝像機標定是確定攝像機參數的一個過程[1],其在三維重建、視覺監控、視覺伺服等領域均有廣泛的應用前景,因此具有重要的理論、實際研究價值。
攝像機標定有傳統標定和自標定。就目前的研究來看,比較常用的還是傳統標定。在工業視覺中,用徑向畸變已經足夠描述非線性畸變,若引入過多的高階畸變參數,不僅不能提高標定精度,反而會引起解的不穩定[2]。本文是在Tsai兩步標定法的基礎上建立的,采用考慮徑向畸變的攝像機模型,標定過程中避免了繁瑣的非線性優化,并進行逆向求解,得標定塊上相對應的空間點的坐標,從而更準確地計算標定誤差。
1 畸變矯正的數學模型
工業視覺中,實際成像與理想的針孔成像之間存在光學畸變誤差。因此需要在理想的攝像機模型中引入畸變模型。在滿足精度要求的前提下,一般情況下只考慮徑向畸變模型,引入過多的畸變模型反而會影響計算精度。為了準確快速的完成標定,本文采用了將能精確反映成像過程的帶有透鏡徑向一階畸變模型引入小孔攝像機模型中[3],如圖1所示。

圖1 考慮鏡頭徑向畸變的攝像機模型
在模型中涉及4個坐標系,并取目標點為P。則其在各個坐標系下的坐標表示如下:(xw,yw,zw)是世界坐標系(owxwywzw)下物體點P的三維坐標。(xc,yc,zc)是點P在攝像機坐標系(ocxcyczc)中的三維坐標。(xu,yu)是理想攝像機模型下P點在攝像機成像平面坐標系(OXY)中的表示,(xd,yd)為P點的實際圖像坐標。(u,v)為P點在計算機圖像坐標系(OUV),以像素為單位。(u0,v0)計算機圖像(幀存)中心坐標。dx、dy分別表示每一個像素在x軸y軸的物理尺寸,f為有效焦距。則點P在計算機圖像坐標系與世界坐標系中存在如下關系式:

上式中的內外參數可通過攝像機標定方法獲得,因此如果已知某空間點的世界坐標,就可以求出該點的計算機圖像坐標;已知目標點的計算機圖像坐標和某些約束條件,就可以求出其對應的空間坐標。
2 攝像機標定的參數求解
本文是根據上述畸變模型(如圖1所示)進行標定算法設計的,需要求解旋轉矩陣R、平移矩陣t、有效焦距f和畸變系數k。具體求解流程如下:
1)求解旋轉矩陣 R,平移向量 t中的Tx,Ty分量[4]:
根據攝像機坐標系(xc,yc,zc)到世界坐標系(xw,yw,zw)的轉換關系,再結合RAC(徑向平行約束)和ZW=0,從而計算Ty的值,然后據R的正交性,求得R中各參數及Tx的值。
2)不考慮畸變時,求解有效焦距f、t的分量Tz估計值。

代入n組特征點,從而求出f、Tz的估計值。
3)考慮畸變時,求f、Tz的優化值和畸變系數k(zw=0)。
畸變模型為:
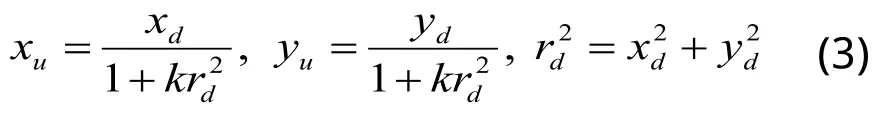
設:

將式(3)、式(4)帶入式(2),并代入n組特征點坐標值,用最小二乘法求解超定線性方程即可求得f、kf、Tz,進而求得f、k、Tz。
3 特征點成像誤差計算模型
空間中某點P在世界坐標系下與攝像機坐標系下的齊次坐標存在如式(5)所示的關系。

將已知的計算機圖像坐標點代入式(6)進行計算,可求得xwi,ywi。在上述逆向求解過程中,由于以上推導是基于透視變換法中的線性針孔成像模型,未考慮畸變。為了計算精確,在式(6)u、v中引入畸變模型(3)得到u`、v`,其中zw=0,利用特征點坐標及其標定求得的參數可求得x`wi、y`wi,從而計算誤差。
4 畸變矯正實驗與數據分析
為了驗證算法的有效性和可行性,本文用HALCON圖像處理軟件平臺進行模擬實驗。本實驗選用的是平面標定塊(如圖2所示),拍攝得到的圖像如圖3所示。相機分辨率為dx=0.01538mm/Pixel,dy=0.01538mm/Pixel,采用的標定模板為6×6個半徑為0.4mm的圓。其中u0=184.5(Pixel)、v0=175(Pixel)。

圖2 平面標定塊
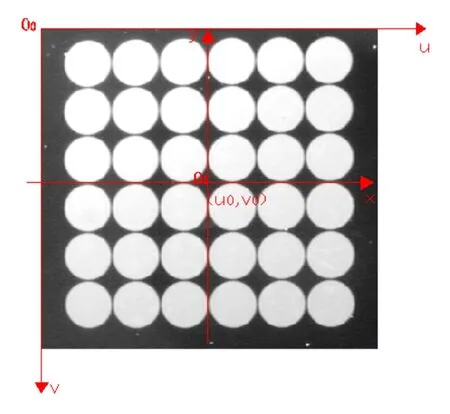
圖3 拍攝的標定塊圖像
1)求標定參數
根據本實驗所選的標定塊,可以得到標定塊上特征點(圓心)的世界坐標(xwi、ywi)單位為mm和相應的圖像坐標(ui、vi)單位為像素Pixel,如表1所示(本文取圖2中前四列右邊的16個圓的圓心坐標作為測試點)。

表2 參數標定結果 (mm)

表3 新特征點與原特征點對比表 (mm)

表1 平面標定塊的特征點的世界坐標和圖像坐標(Zw=0)
據表1中的數據,運用本文的標定算法得參數結果如表2所示。
2)求特征點成像誤差
據表2所求得參數及本文的逆向求解算法得到相應的新世界坐標,其中zw=0,特征點的新世界坐標(x`wi、y`wi)和原世界坐標(xwi、ywi)如表3所示。
誤差的計算可采用空間世界坐標的絕對誤差和相對誤差來表示。經計算得絕對誤差Ew=0.01449mm,相對誤差為ew=4.26‰。
5 結論
在該算法中誤差的來源主要有[5]:1)標定板的不平度引入的誤差。2)CCD相機與光學成像產生的誤差。CCD相機光敏面上的中心距限制了測量的分辨率。
本文采用帶有徑向畸變的攝像機模型,逆向求特征點,再與原特征點進行數據比較,精確地計算出標定誤差。實驗驗證該算法相對誤差達4.26‰,可以快速、準確的完成標定,并且準確計算誤差,提高了算法的精度。同時該算法還可以應用在其他有圖像畸變的場合進行鏡頭誤差評定,即判斷畸變矯正的必要性,如果通過本文算法得到畸變誤差足夠小,則可略去矯正環節,進而提高了整個計算的效率和準確度,在機器視覺領域具有較強的實用性。
[1]徐杰.機器視覺中攝像機標定Tsai兩步法的分析與改進[J].北京科技大學學報,2010,32(4):45-48.
[2]趙宣銘.一種基于Tsai法的攝像機改進標定法[J].西安工程大學學報,2011,25(4):560-564.
[3]李君蘭,張大衛,王以忠,等.面向封裝的顯微視覺定位系統[J].光學精密工程,2010,18(4):965-967.
[4]王建華,馮帆,梁偉,等.基于matlab的攝像機標定系統的設計與實現[J].計算機與數字工程.2012,269(3),97-99.
[5]張海,付偉,高榮杰.機器視覺測量中相機兩步標定法的改進[J].華東交通大學學報.2012,46(3):77-80.

