磁耦合諧振無線電能傳輸系統(tǒng)的輸出魯棒控制

劉　軍，杜　歡

（西安理工大學自動化學院，陜西西安710048）

磁耦合諧振無線電能傳輸系統(tǒng)的輸出魯棒控制

劉軍，杜歡

（西安理工大學自動化學院，陜西西安710048）

摘要：磁耦合諧振無線電能傳輸系統(tǒng)的負載和諧振參數(shù)會因為受到外界環(huán)境的影響而發(fā)生變化，系統(tǒng)工作頻率發(fā)生隨機漂移，導致模型參數(shù)存在不確定性。針對參數(shù)不確定下的輸出魯棒控制問題，基于H∞控制理論，應用matlab魯棒控制工具箱設計H∞控制器，并利用結(jié)構(gòu)奇異值法分析了閉環(huán)系統(tǒng)的魯棒穩(wěn)定性和魯棒性能。結(jié)果表明，在H∞控制器的作用下，實現(xiàn)了閉環(huán)攝動系統(tǒng)的輸出魯棒控制。并為這種高階非線性不確定閉環(huán)攝動系統(tǒng)提供一種通用的控制器設計方法。

關(guān)鍵詞：無線電能傳輸；諧振式；不確定性；H∞控制；matlab工具箱；魯棒性

1　引言

磁耦合諧振無線電能傳輸系統(tǒng)（magnetically coupled resonant wireless power transfer，MCR-WPT)在實際工作中，負載和諧振參數(shù)會因為受到外界環(huán)境如溫度、諧振線圈距離的影響而發(fā)生變化，系統(tǒng)工作頻率發(fā)生隨機漂移，導致模型參數(shù)存在不確定性。因此，希望設計一種控制器，使控制系統(tǒng)在實際應用中具有一定的魯棒性［1-5］。

在提高系統(tǒng)的魯棒性方面，以往的bang-bang控制、PID控制、滑模變結(jié)構(gòu)控制這一類單目標控制方法［6-9］雖然易于實現(xiàn)且具有一定的魯棒性，但其控制精度和對負載變化的適應能力較差，且均未考慮系統(tǒng)可能存在的不確定因素及外部擾動，當實際系統(tǒng)與原來的標稱系統(tǒng)出現(xiàn)偏差時，控制器的精度及性能會變差，控制系統(tǒng)將無法達到較理想的控制效果。

本文首先利用廣義狀態(tài)空間平均（generalized state space averaging，GSSA）建模法對磁耦合諧振無線電能傳輸系統(tǒng)進行建模，利用線性分式變換分離GSSA模型的確定部分與不確定部分。基于H∞控制理論，應用matlab魯棒控制工具箱設計H∞控制器，并利用結(jié)構(gòu)奇異值理論分析閉環(huán)系統(tǒng)的魯棒穩(wěn)定性和魯棒性能。

2　系統(tǒng)GSSA建模

2.1 GSSA建模方法

基于頻域分解的GSSA建模法的基本思想是用傅里葉級數(shù)的形式來描述時域周期信號，用共軛的低階諧波分量來近似原始信號，并將非線性環(huán)節(jié)近似線性化處理，然后通過信號還原得到時域原始信號的包絡及其近似解［10］。

時域連續(xù)周期性信號x（t）可以分解成Fourier級數(shù)的形式。

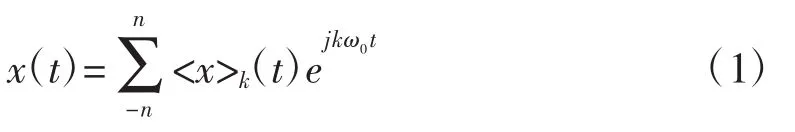
式（1）中，n表示第n次諧波的分量,ω0=2π/T是x（t）基波的角頻率，＜x＞k（t）為x（t）的k階Fourier級數(shù)的系數(shù)，即為n次諧波分量的幅度值，傅里葉級數(shù)有共軛對稱性、微分特性、卷積特性、線性特性4個重要性質(zhì)，不再贅述。

2.2系統(tǒng)建模

磁耦合諧振無線電能傳輸系統(tǒng)的電路拓撲如圖1所示。

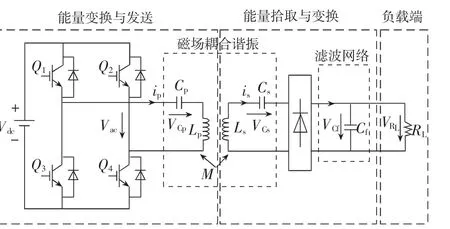
圖1　 MCR-WPT系統(tǒng)的電路拓撲

圖1中左半部分是電能的發(fā)射端，包含工作在ZCS模式下的高頻逆變環(huán)節(jié)和LpCp串聯(lián)諧振環(huán)節(jié)；副邊部分作為能量拾取端，包括串聯(lián)諧振、整流及濾波三個環(huán)節(jié)。為了有效地傳輸電能，發(fā)射線圈和接收線圈的自諧振頻率設置為同一頻率，即為系統(tǒng)的諧振頻率。

由電路拓撲得到系統(tǒng)時域非線性微分方程，其中，狀態(tài)變量為［ip,is,VCs,VCp,VCf］T。

MCR-WPT系統(tǒng)工作過程中，由于逆變器工作在ZCS模式，保證各個儲能元件上的能量呈正弦規(guī)律變化，因此，對時域微分方程做Fourier級數(shù)分解時，交流信號只考慮基波。

分解后得到系統(tǒng)的頻域線性微分方程，其中，以電路變量各傅里葉系數(shù)的實、虛部依次作為廣義狀態(tài)變量，即

x（t）=［Re＜ip＞1，Im＜ip＞1，Re＜is＞1，Im＜is＞1，Re＜VCp＞1，

Im＜VCp＞1，Re＜VCs＞1，Im＜VCs＞1，＜VCf＞0］T（2）

基于頻域線性微分方程，得到以式（2）作為狀態(tài)變量的廣義狀態(tài)空間描述（GSSA模型）如下。

x（.t）=Ax（t）＋Bu（t）（3）

其中，u∈R1×1作為控制輸入即為MCR-WPT系統(tǒng)的直流輸入電壓Vdc，A∈R9×9和B∈R1×9分別為系統(tǒng)矩陣和輸入矩陣，且

3　參數(shù)攝動下的系統(tǒng)不確定性模型

在實際工作中，負載RL和工作頻率ω具有不確定性，可以用以下式子描述。

ω0和RL0分別表示ω和RL的標稱值，pω,pr和δω,δr分別代表ω和RL的可能的（相對）攝動變化范圍。令pω=0.2,pr=0.4,以及-1≤δω,δr≤1，則表示ω在標稱值ωˉ的±20%的范圍內(nèi)變化，RL在標稱值RL0的±40%的范圍內(nèi)變化。

采用線性分式變換，分離RL和ω的確定與不確定部分，表示為：

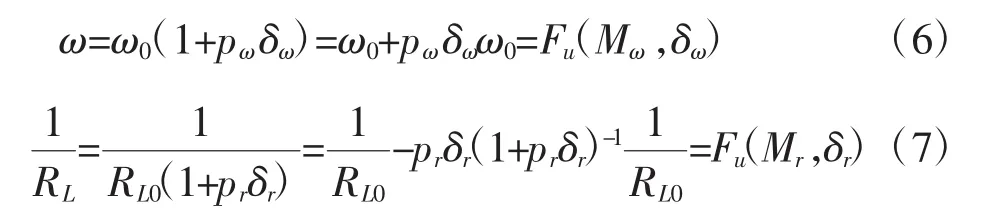
從而分離GSSA模型的標稱部分和不確定部分，得到MCR-WPT系統(tǒng)的不確定性模型，狀態(tài)方程表示為：

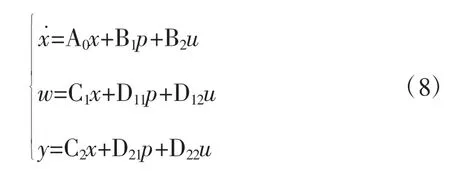
式（8）用一個含攝動反饋的線性動力學系統(tǒng)G=Fu（Gmds,Δ）表示，如圖2所示。

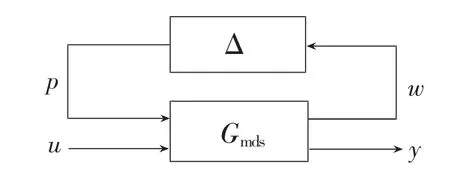
圖2　系統(tǒng)不確定模型

式（8）中，x∈R9×1為狀態(tài)變量，u∈R1×1為控制輸入，即MCR-WPT系統(tǒng)的直流輸入電壓值Vdc，y∈R1×1為測量輸出（負載輸出電壓VCf），Δ為一個只含δω和δr的不確定對角陣即

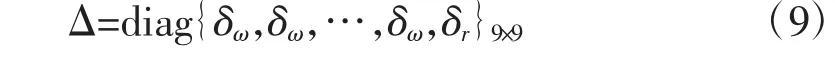
p、w∈R9×1分別為攝動塊Δ的輸入和輸出

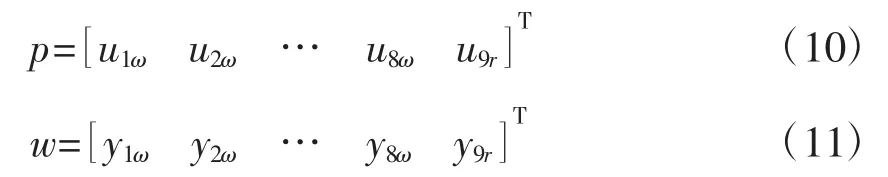
Gmds是廣義標稱模型，

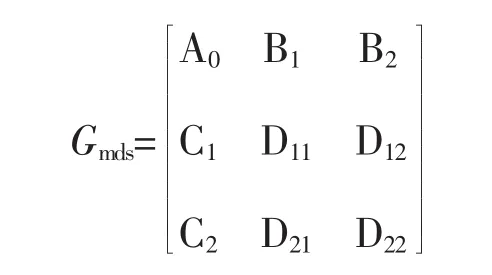
式（8）中各矩陣如下：

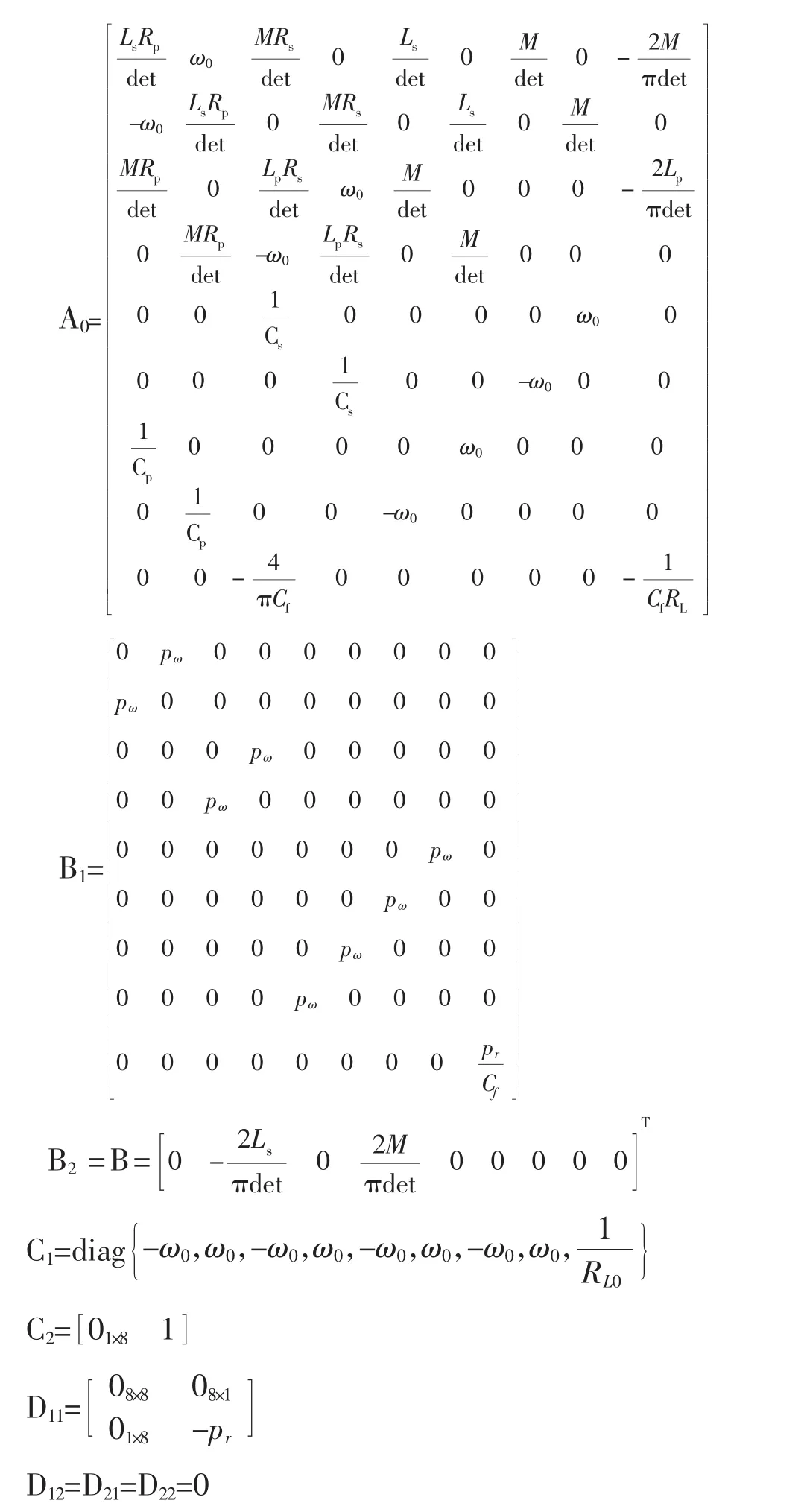
在matlab里創(chuàng)建系統(tǒng)矩陣Gmds，保存為變量Gmds。Gmds=pck（A0,［B1，B2］,［C1，C2］,［D11D12；D21D22］）;

4　 H∞控制器設計

4.1標準H∞控制問題描述

如圖3所示為標準H∞控制問題。

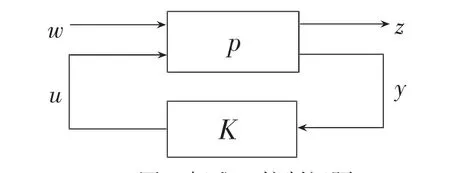
圖3　標準H∞控制問題

其中z為被控輸出信號, y為測量信號, w為外部輸入信號, u為控制信號。

標準H∞控制問題就是求一正則控制器K（s），滿足

1）使閉環(huán)系統(tǒng)內(nèi)穩(wěn)定；

2）使w到z的傳遞函數(shù)的H∞范數(shù)滿足。

式（12）表示最優(yōu)H∞控制問題。式（13）則表示H∞次優(yōu)控制問題。

4.2系統(tǒng)連接

MCR－WPT閉環(huán)系統(tǒng)框圖如圖4所示。

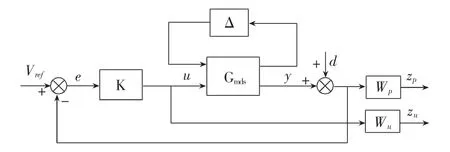
圖4　 MCR－WPT閉環(huán)系統(tǒng)框圖

設計H∞控制器之前，首先基于matlab創(chuàng)建系統(tǒng)的開環(huán)系統(tǒng)結(jié)構(gòu)。圖5所示為系統(tǒng)的開環(huán)結(jié)構(gòu)圖。

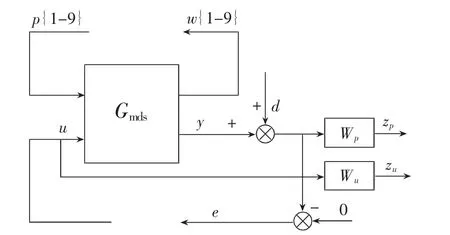
圖5　開環(huán)系統(tǒng)結(jié)構(gòu)

圖5中，Wp是一個低通濾波函數(shù)，代表干擾的頻譜特性，Wu描述中低頻參數(shù)的頻率特性，可以選擇為一常數(shù)并進行適當調(diào)整，取

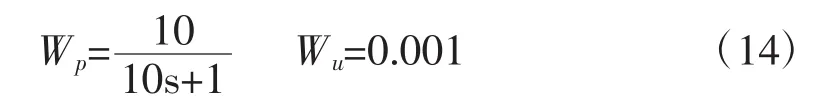
不確定塊Δ的輸入變量w和輸出變量p都包含9個元素；控制量u、外加干擾d、被調(diào)輸出zp、zu和e只有一個元素。

sysic指令用來創(chuàng)建開環(huán)系統(tǒng)結(jié)構(gòu)，保存為變量sys_ic，系統(tǒng)參數(shù)如表1所示。

systemnames=’GWp Wu’;

inputvar=’［p{9};d;u］’;

outputvar=’［G(1:9);Wp;Wu;－G（10）－d］’;

input_to_G=’［p;u］’;

input_to_Wp=’［G（10）＋d］’;

input_to_Wu=’［u］’;

sysoutname=’sys_ic’;

cleanupsysic=’yes’;

sysic

變量sys_ic包含11個輸入和12個輸出，如圖6所示。

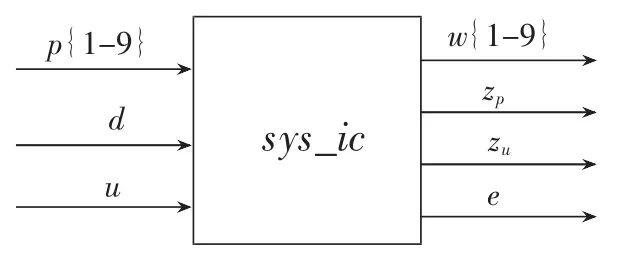
圖6　開環(huán)系統(tǒng)結(jié)構(gòu)的變量表示

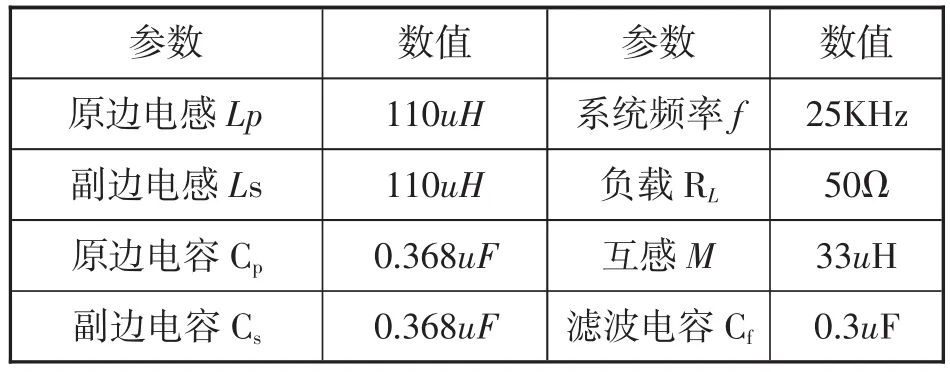
表1　系統(tǒng)參數(shù)表

轉(zhuǎn)換為H∞標準控制問題，結(jié)構(gòu)框圖如圖7所示。

圖7　 H∞標準控制框圖

利用sel指令從變量sys_ic中提取傳遞函數(shù)矩陣P（增廣對象），保存為變量hin_ic。

hin_ic= sel（sys_ic,10:12,10:11）

H∞控制下的閉環(huán)系統(tǒng)的線性分式變換形式如圖8所示。

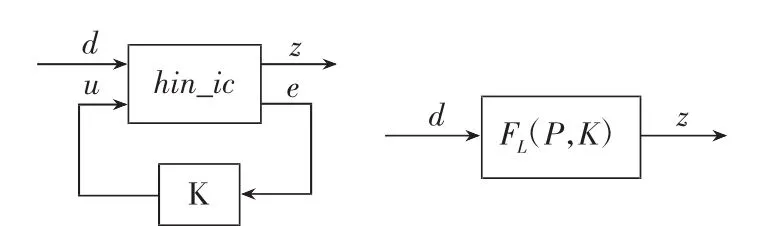
圖8　 H∞控制系統(tǒng)的線性分式變換形式

4.3 H∞次優(yōu)控制器設計

如圖8所示，F(xiàn)L（P，K）是標稱閉環(huán)系統(tǒng)從干擾（變量d）到輸出z=［zp,zu］T的傳遞函數(shù)。求一穩(wěn)定的控制器K，該控制器能使FL（P，K）的H∞范數(shù)小于一給定的性能參數(shù)γ。

‖F(xiàn)L（P，K）‖∞＜γ（γ＞0）基于給定的開環(huán)系統(tǒng)，利用指令hinfsyn計算H∞次優(yōu)控制器，hinfsyn的語法和輸入、輸出參數(shù)如表2、表3所示。［k,clp］= hinfsyn（p,nmeas,ncon,glow,ghigh,tol）。基于以上分析，通過以下程序求得H∞次優(yōu)控制器。

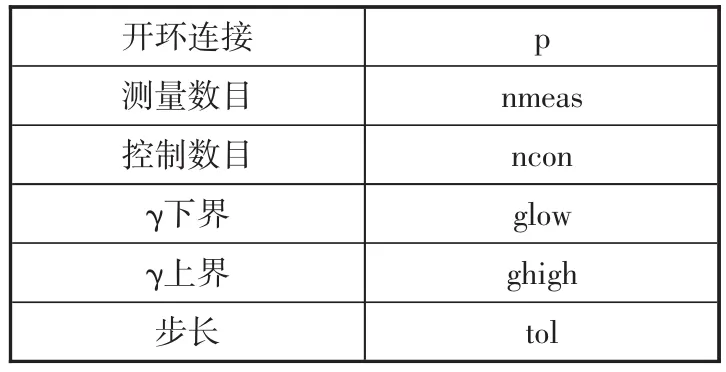
表2　輸入?yún)?shù)

表3　輸出參數(shù)

nmeas = 1;

ncon = 1;

gmin = 1;

gmax = 10;

tol = 0.001;

hin_ic = sel（sys_ic,10:12,10:11）;

［k,clp］= hinfsyn（hin_ic,nmeas,ncon,gmin,gmax,tol）

5　基于結(jié)構(gòu)奇異值（μ方法）的閉環(huán)系統(tǒng)性能分析

5.1標稱閉環(huán)系統(tǒng)性能分析

如圖9所示為標稱系統(tǒng)的閉環(huán)結(jié)構(gòu)，此時系統(tǒng)的不確定部分為考慮在內(nèi)。

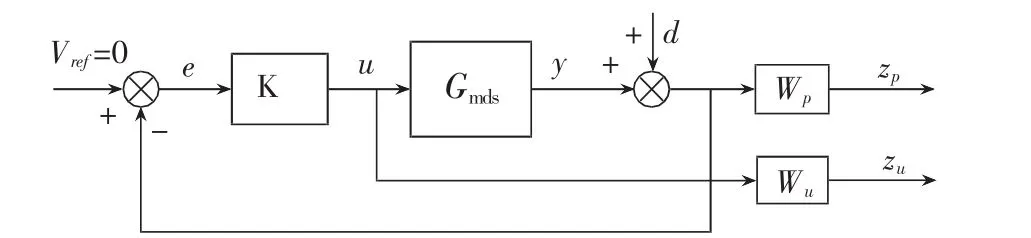
圖9　標稱系統(tǒng)的閉環(huán)結(jié)構(gòu)

圖9中，其標稱性能指標可以采用從外部擾動輸入d到被調(diào)輸出z=［zp, zu］T之間傳遞函數(shù)矩陣Tdz（s）的H∞范數(shù)來描述，即：

當式（15）成立時，則表示H∞控制器能有效地把外部干擾的影響抑制到可允許的范圍內(nèi)，系統(tǒng)內(nèi)部穩(wěn)定且滿足預設標稱性能。圖10所示是閉環(huán)系統(tǒng)從外部干擾d到被調(diào)輸出z的響應曲線。

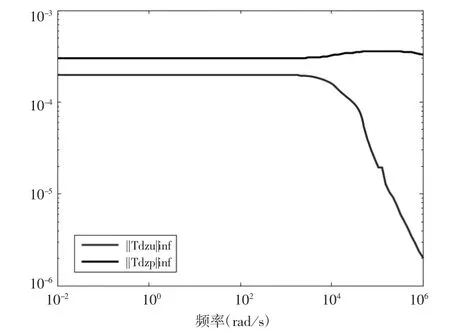
圖10　閉環(huán)系統(tǒng)標稱性能

如圖10所示，在H∞控制作用下，閉環(huán)系統(tǒng)在頻率［10－2106］范圍內(nèi)響應的值均小于1。表明該控制系統(tǒng)不僅是內(nèi)部穩(wěn)定的，而且滿足了預設的標稱性能指標。

5.2魯棒穩(wěn)定性分析

將H∞控制系統(tǒng)轉(zhuǎn)換為標準的M－Δ結(jié)構(gòu)。

圖11　標準M－Δ結(jié)構(gòu)圖

圖11中，M為閉環(huán)系統(tǒng)的廣義標稱對象，包含魯棒控制器K,標稱對象Gmds及性能加權(quán)函數(shù)。

若傳遞函數(shù)矩陣M（s）是穩(wěn)定的、實有理的，且有np＋nd個輸入和nw＋nz個輸出（np=9 nd=1 nw=9 nz=2）,那么M（s）可以表示成以下的子矩陣分塊形式：

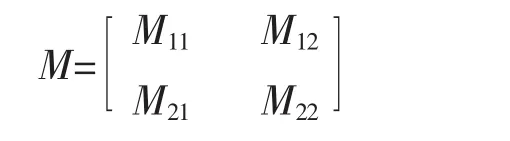
M11有np個輸入和nw個輸出，攝動塊Δ∈Cnw×np對應子矩陣M11的不確定性傳遞函數(shù)。穩(wěn)定性定理可以等價為：

在H∞控制器的作用下，μΔ（M11）在頻率范圍［10-2,106］的響應曲線如圖12所示。

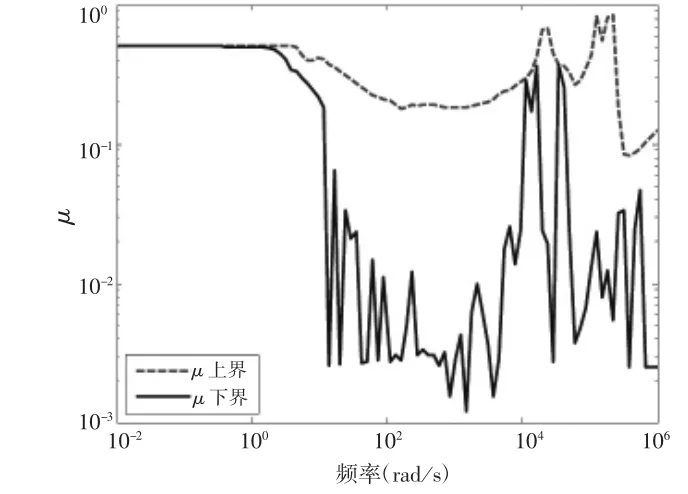
圖12　閉環(huán)系統(tǒng)的魯棒穩(wěn)定性

如圖12所示，在整個［10-2,106］頻率范圍內(nèi)，子矩陣塊M11關(guān)于攝動塊Δ的結(jié)構(gòu)奇異值μΔ（M11）都小于1，表明在參數(shù)攝動下，閉環(huán)系統(tǒng)具有魯棒穩(wěn)定性。且μΔ（M11）的峰值表示最大攝動范圍。

5.3魯棒性能分析

在不確定矩陣Δ∈Cnw×np中加入性能不確定全塊Δp∈Cnd×nz組成一個增廣攝動矩陣Δ∈C(nw+nd)×(np+nz)，如圖13所示。

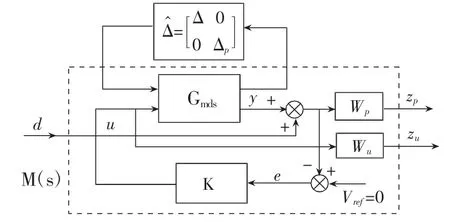
圖13　魯棒性能框圖

從擾動輸入d到被調(diào)輸出z=［zp, zu］T的傳遞函數(shù)的H∞范數(shù)

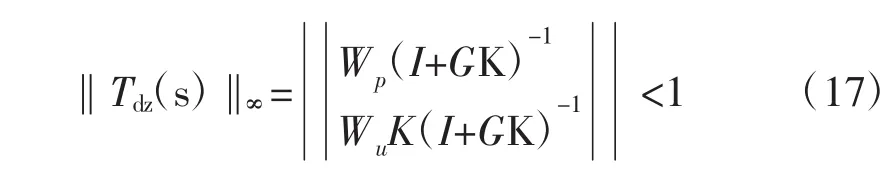
當且僅當

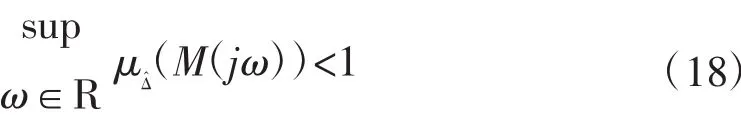
成立。

根據(jù)式（18），可知閉環(huán)系統(tǒng)是否達到了預設的魯棒性能指標。

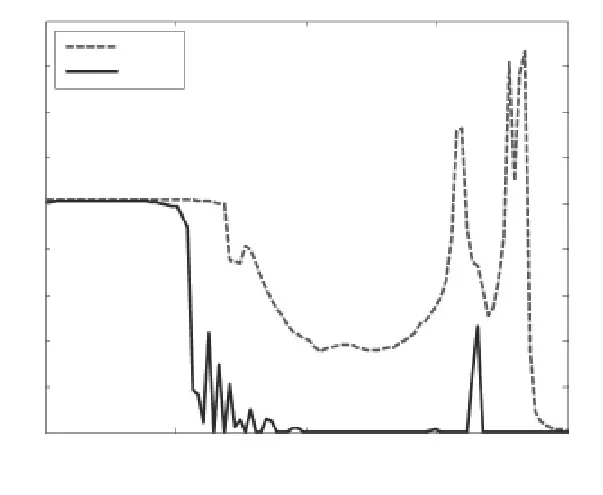
圖14　閉環(huán)系統(tǒng)的魯棒性能

由圖14可知，在［10-2,106］頻率范圍內(nèi)，μΔ0（M）的上、下界的頻率響應值都比1小，即驗證了H∞控制系統(tǒng)的魯棒性能。

6　參數(shù)變化下閉環(huán)攝動系統(tǒng)的輸出響應

魯棒控制系統(tǒng)對屬于這個集合的所有攝動對象均應保證正常工作的屬性。本節(jié)通過測試攝動閉環(huán)系統(tǒng)，來驗證H∞控制對閉環(huán)攝動系統(tǒng)的魯棒性。

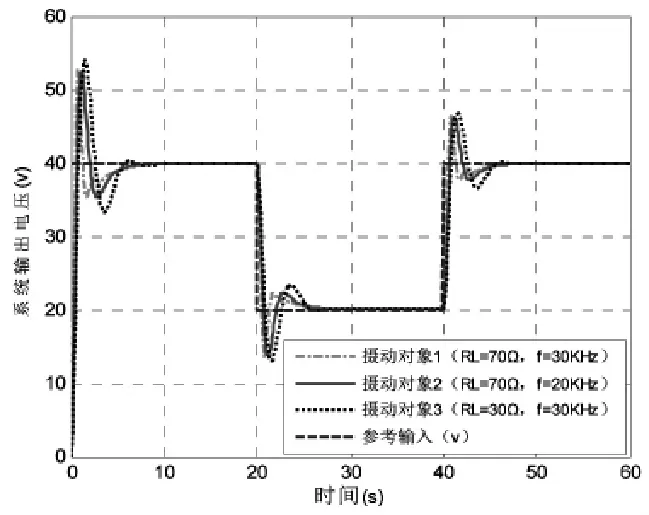
圖15　 3個閉環(huán)攝動系統(tǒng)在給定參考輸入下的輸出響應

標稱值ω0=25kHz,RL0=50Ω，令pω=0.2,pr=0.4,以及-1≤δω,δr≤1。這里δω,δr分別取+1,-1。得到Δ的3種不同矩陣形式，對應參數(shù)變化下的3種的閉環(huán)攝動對象，驗證H∞控制器的控制效果。圖15和圖16分別是參數(shù)變化下3個攝動閉環(huán)系統(tǒng)在給定參考輸入和干擾作用下的時域響應曲線。

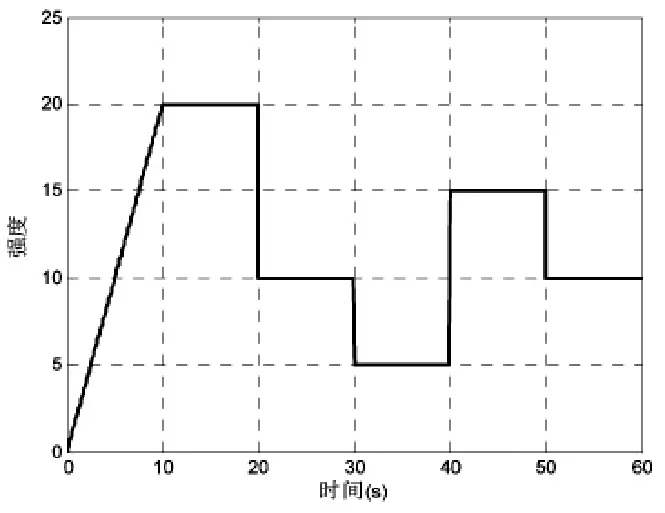
（a）擾動信號

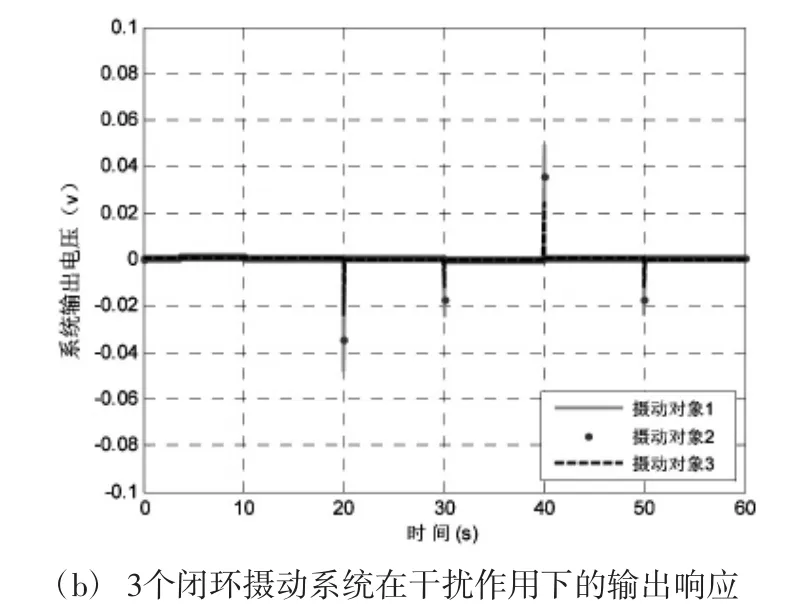
圖16 3個閉環(huán)攝動系統(tǒng)在干擾作用下的時域響應曲線

基于上述分析，針對攝動范圍內(nèi)的所有可能的控制對象，當給定參考輸入和干擾輸入時，攝動范圍內(nèi)所有閉環(huán)攝動系統(tǒng)暫態(tài)響應曲線如圖17和圖18所示。

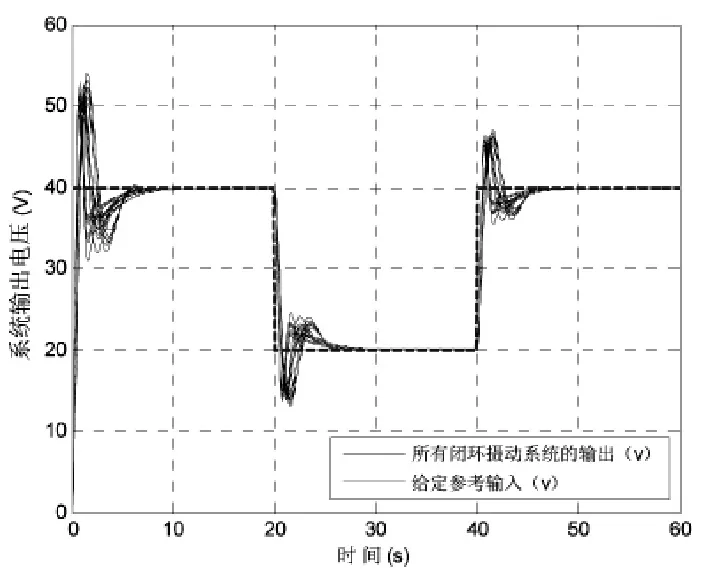
圖17　閉環(huán)攝動系統(tǒng)在給定輸入下的輸出響應

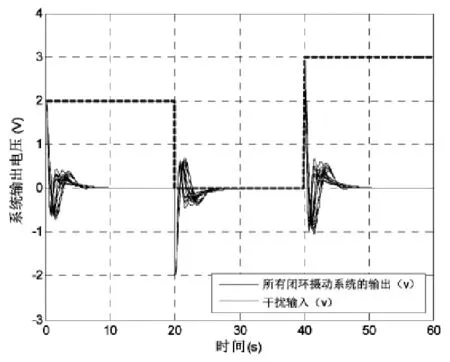
圖18　閉環(huán)攝動系統(tǒng)在干擾輸入作用下的輸出響應

由圖17可知，在給定輸入的情況下，超調(diào)量都不大于29%，動態(tài)調(diào)節(jié)時間在5s左右。這表明在H∞控制作用下，實現(xiàn)了閉環(huán)攝動系統(tǒng)的無靜差魯棒跟蹤控制。

由圖18可知，閉環(huán)攝動系統(tǒng)在受到干擾輸入的影響下，系統(tǒng)的輸出在經(jīng)過一定調(diào)節(jié)時間后都趨于0并最終穩(wěn)定在0,這表明干擾對閉環(huán)攝動系統(tǒng)的輸出幾乎無影響。

總體說來，在H∞控制作用下，針對有界攝動范圍內(nèi)的所有可能的控制對象，閉環(huán)系統(tǒng)不僅是魯棒穩(wěn)定的，而且具有一定的魯棒性能。

7　結(jié)束語

本文利用基于頻域分解的廣義狀態(tài)空間平均法對磁耦合諧振無線電能傳輸系統(tǒng)進行建模，基于H∞控制理論，采用MATLAB魯棒控制工具箱設計了H∞控制器，綜合考慮參數(shù)不確定性和外部擾動因素影響下的閉環(huán)攝動系統(tǒng)，在H∞控制作用下，實現(xiàn)了閉環(huán)系統(tǒng)的輸出魯棒控制。

參考文獻：

［1］趙爭鳴，張藝明，陳凱楠.磁耦合諧振式無線電能傳輸技術(shù)新進展［J］.中國電機工程學報，2013，33（3）：1－12.

［2］黃學良，譚林林.無線電能傳輸技術(shù)研究與應用綜述［J］.電工技術(shù)學報，2013，28（10）：1－9.

［3］Kurs A，Karalis A，Moffatt R，et al.Wireless power transfer via strongly coupled magnetic resonances［J］.Science，2007，317（5834）：83－86.

［4］韓騰，卓放，閆軍凱等.非接觸電能傳輸系統(tǒng)頻率分叉現(xiàn)象研究［J］.電工電能新技術(shù)，2005，24（2）：44－47.

［5］Zhang Xian，Yang Qingxin，Chen Haiyan，et al.Research on characteristics of frequency splitting in electromagnetic coupling resonant power transmission systems［J］.Proceedings of the CSEE，2012，32（9）：167－173（in Chinese）

［6］傅文珍，張波，丘東元.頻率跟蹤式諧振耦合電能無線傳輸系統(tǒng)研究［J］.變頻器世界，2009（8）：41－46.

［7］王智慧.基于包絡線調(diào)制的非接觸電能傳輸模式研究［D］.重慶大學，2009.

［8］唐春森.非接觸電能傳輸系統(tǒng)軟開關(guān)工作點研究及應用［D］.重慶大學，2009.

［9］戴欣，孫躍.感應電能傳輸系統(tǒng)能量注入控制方法研究［J］.電子科技大學學報，2011（1）：69－72.

［10］Robust control for an uncertain LCL resonant ICPT system using LMI methodYan－Ling Lin，Yue Sun，Xin Dai.Control Engineering Practice 21（2013）31－41.

Output robustness control of the magnetic coupling resonant wireless power transmission system

LIU Jun，DU Huan
（College of Automation，Xi＇an University of Technology，Xi＇an 710048，China）

Abstract：The loads and resonant parameters of the magnetic coupling resonant wireless power transmission system are subjected to the influence of the external environment and change，and the operating frequency may randomly drift to make the model parameters uncertain.In order to solve the problem of the robustness output control with uncertain parameters，the H∞controller is designed by using the Matlab robust control toolbox based on H∞control theory.The robustness stability and performance of the closed－loop system are analyzed by using the structure singular method.The experimental results show that the H∞controller realizes the output robustness control of the closed－loop perturbation system and provides a general design method for such high－order nonlinear uncertain closed－loop perturbation system.

Key words：wireless power transmission；resonant；uncertainty；H∞control；Matlab Toolbox；robustness

中圖分類號：TM724

文獻標識碼：A

文章編號：1005—7277（2015）05—0016—07

作者簡介：

劉軍（1963－），男，陜西西安人，博士，教授，博士生導師，研究方向為無線電能傳輸。

杜歡（1990－），女，陜西西安人，碩士，研究方向為無線電能傳輸。

收稿日期：2015－01－05