石墨烯能帶中的重疊矩陣效應:Tight-Binding方法在模擬中的研究

李 偉，徐 鑫，劉 潤，2

(1. 鎮江船艇學院，鎮江212000;2. 北京師范大學核科學與技術學院，北京100875)

1 引 言

由于石墨烯特殊的電子性能和在電子器件上廣闊的應用前景，其引起了全世界越來越多的關注［1］. 基于石墨烯的電子器件有希望克服半導體硅技術在導電性能上的限制［2］，甚至可能取代硅成為未來的固態器件的核心［3］. 當石墨烯材料導電時，電子受到激發從價帶克服能帶間隙躍遷到導帶，因此對石墨烯能帶的研究是非常有意義的，這對邏輯電路和其他電子設備的應用是必不可少的［4］.

認識石墨烯，首先就必須對其的能帶有足夠清晰的了解. 無論從實驗上還是理論上，前人都已經做了相當全面的工作. Konschuh 等人［5］主要研究了考慮自旋-軌道(s，p，和d)耦合的緊束縛模型，重點研究了d 軌道對高對稱點(K 點)能帶的影響. Harrison［6］從方法學的角度，利用Louie 微擾法，在緊束縛模型中引入了s 軌道激發態，這種方法得到的導帶結果與實驗符合得很好.Reich 等人［7］用緊束縛方法研究了石墨烯的價帶和導帶，發現最近鄰緊束縛模型只在有限的波矢范圍內有效，如果增加相互作用原子的數目，即將緊束縛模型推廣到第三近鄰原子，所得的結果在整個布里淵區都能較準確描述第一性計算結果.

本文作為基礎研究，通過編寫Matlab 程序，研究了不同大小(s≤0.1 和s≥0.1)的重疊積分參量對單層石墨烯能帶的影響. 對比了正交基矢和非正交基矢的能帶的變化，對比了重疊矩陣對高對稱點(Γ 點，-點和K 點)的影響，期望對相關領域的研究者有一定的參考價值.

2 理論模型

碳原子有6 個電子，形成1s22s22p2這樣的電子排布. 當碳原子與其他元素形成化合物時，由于s 和p 軌道的比例性，2s 和2p 上的軌道會互相混合，形成不同的雜化軌道. 石墨烯是sp2雜化:2s 軌道與2px和2py軌道重疊，產生三個新的sp2軌道，每個軌道上有一個電子. 2pz軌道不變并與每個sp2軌道配對. 由于相鄰碳原子sp2軌道的重疊，形成了成鍵σ 和反鍵σ*. 這三個成鍵σ 在同一個面內且互相之間的夾角為120°，因此石墨烯是正六邊形平面蜂窩形結構(如圖1). pz軌道的重疊垂直于正六邊形平面，產生了成鍵π 和反鍵π*. 與1s 的芯能級相比，sp2軌道的較低結合能被定義為半芯能級，而pz軌道的最低結合能被認為是價帶. pz的能級重疊產生了價帶(成π 鍵)和導帶(反π*鍵). 因此，石墨烯的力學性能決定于σ 鍵，而π 鍵主要影響石墨烯的電性質.

2.1 電子能帶

對于石墨烯(如圖1)，一個晶胞中含有2 個原子，分別為A 原子和B 原子，假設A 原子為中心，三個與他最近鄰的B 原子的位置分別為

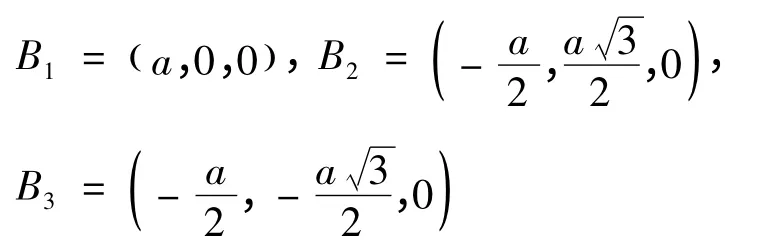
使用緊束縛方法解石墨烯晶胞中π 電子特征方程. 這里，只考慮了最近鄰原子間的相互作用，所以，A 型或者B 型原子中的任意一個原子在它周圍都有3 個與它不同類型的原子是它的最近鄰原子，對角的哈密頓量矩陣元和重疊積分可寫成:

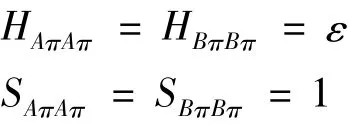
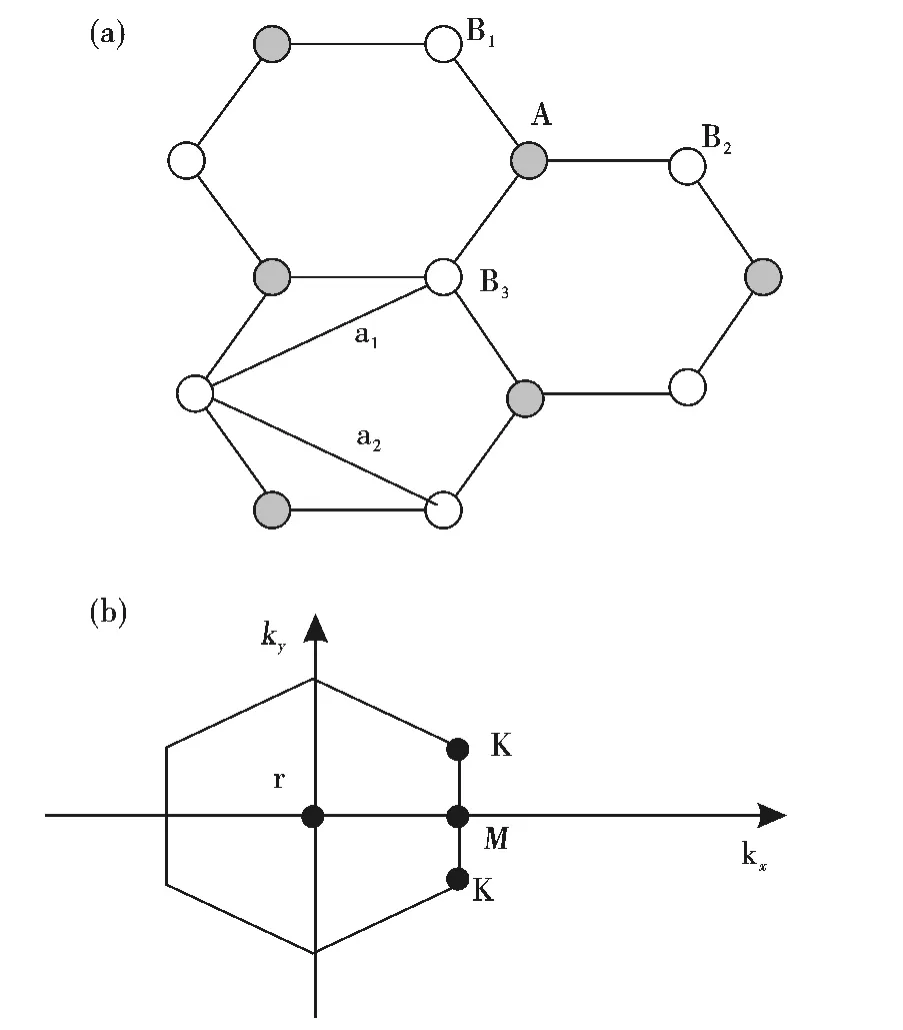
圖1 (a)真實空間中，石墨烯晶格的正格矢; (b)石墨烯的第一布里淵區，以及倒格矢和布里淵區里的高對稱點Г，M，K，K’Fig. 1 (a)The graphene lattice vector in real space;(b)Graphene first Brillouin zone，as well as reciprocal lattice vectors in the Brillouin zone and high symmetry points Г，M，K，K’

對于矩陣元HAπBπ和SAπBπ，一個原子到最近鄰的三個原子的向量為

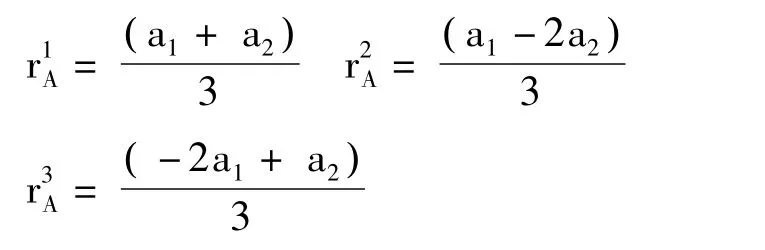
可以算出非對角的哈密頓矩陣元和重疊積分矩陣元

解這個方程，能得到石墨烯的價帶和導帶的能量色散關系.

這里ε 是費米能級上任意一個能量參考點. 在正交緊束縛模型中，將它一般設為0 eV. ( + )?υ，( - )?c，υ 和c 分別代表價帶和導帶. ω ()是f ()的絕對值，

另外，根據第一性原理［5］所擬合的參數為

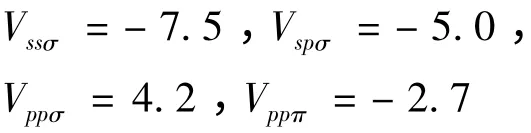
計算中，Es= -8.3eV，Ep= 0eV［6］.

2.2 態密度

石墨烯的態密度計算公式［8］為

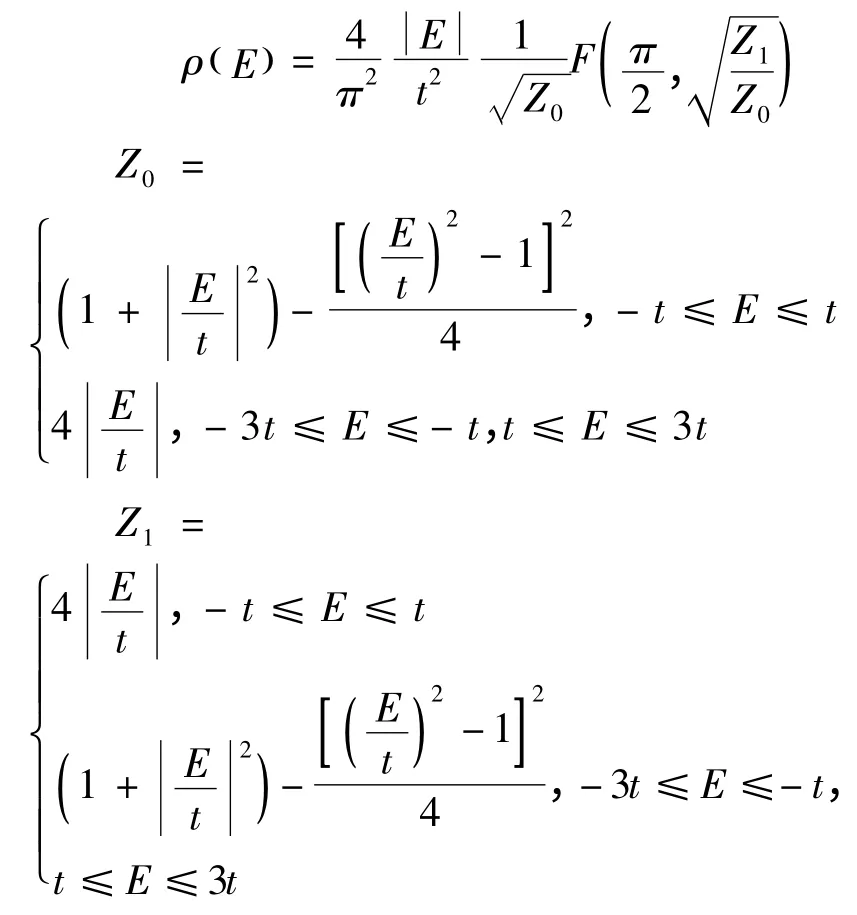
3 結果與討論

3.1 重疊矩陣效應

圖2 中所示為正交基矢和非正交基矢(s =0.02)下，導帶(π* )和價帶(π)在- -Γ-K- -方向上的能帶圖. 圖中表明，在正交基矢下，Γ 點的能量差為6= 16.2 eV(γ0為π 能帶的跳躍參數，此處取γ0= -2.7 )，-點的能量差為2= 5.4 eV，相差3 倍. 非正交基矢下，導帶和價帶都向上有一定平移，值得一提的是，重疊矩陣的加入會導致Γ 點的能量差不等于6，然而對-點無影響，并且重疊效應對K 點附近電子行為沒有明顯影響，表明K 點附近電子與軌道重疊不相關.

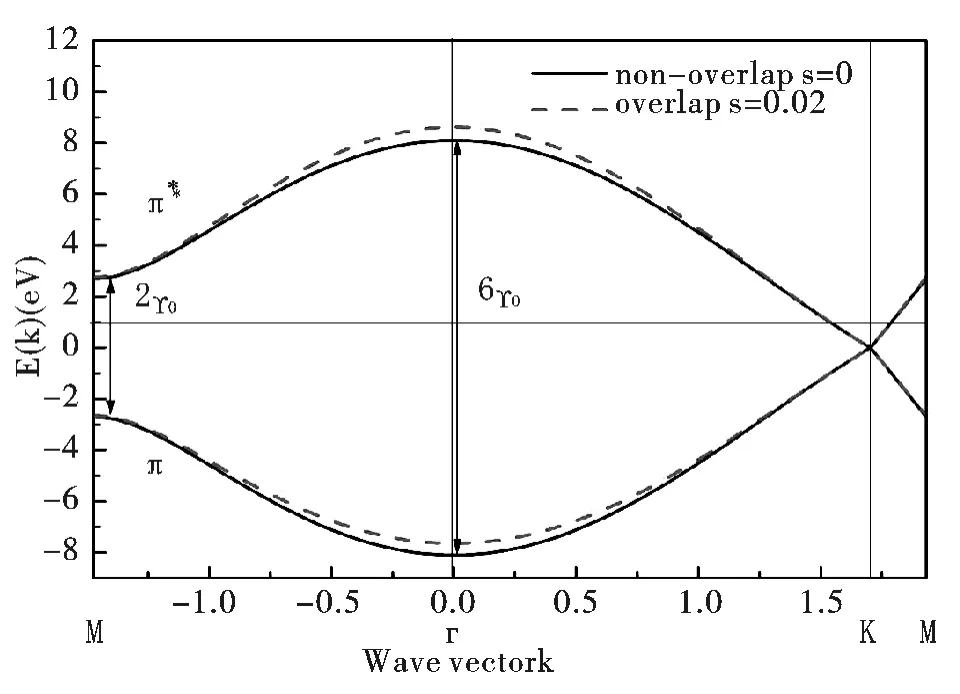
圖2 正交基矢和非正交基矢下，- -Γ -K - -方向上的能帶圖Fig. 2 The energy band of - -Γ -K - - direction in orthogonal and non-orthogonal basis

Reich 等人［7］中認為軌道重疊效應影響比較小，因此參數取值應在s≤0.1 范圍內. 為了探索s的影響，這里將分為兩種情況 (s ≤0.1 和s ≥0.1)討論. 第一種情況(s≤0.1)，在圖3 (a)中，s 越小，導帶越靠近費米面，而價帶越遠離費米面，極限情況是s =0，對應于圖3 的非重疊情況，此時，兩條能帶關于費米面對稱;第二種情況(s≥0.1)，在圖3 (b)中，s 越大，導帶越遠離費米面，而價帶越靠近費米面，但是價帶的變化遠遠小于導帶，導帶在s =0.3 時，Γ 點能量可達到80eV，因此在Γ 點電子的激發是很困難的.在s=0.4 時，能帶已不再呈拋物線狀(如圖4)，變化趨勢劇烈，在Γ 和-點的能隙消失，已經失去了物理意義，只能代表理論模擬上可能的情況.

綜上所述，s 越小，導帶越靠近費米面，而價帶越遠離費米面，取值在s≤0.1 范圍內能保持原子在實際空間中重疊所引起的能帶的改變，太大則會導致物理上失效. 很多情況下，認為s 太小，一般將其忽略.

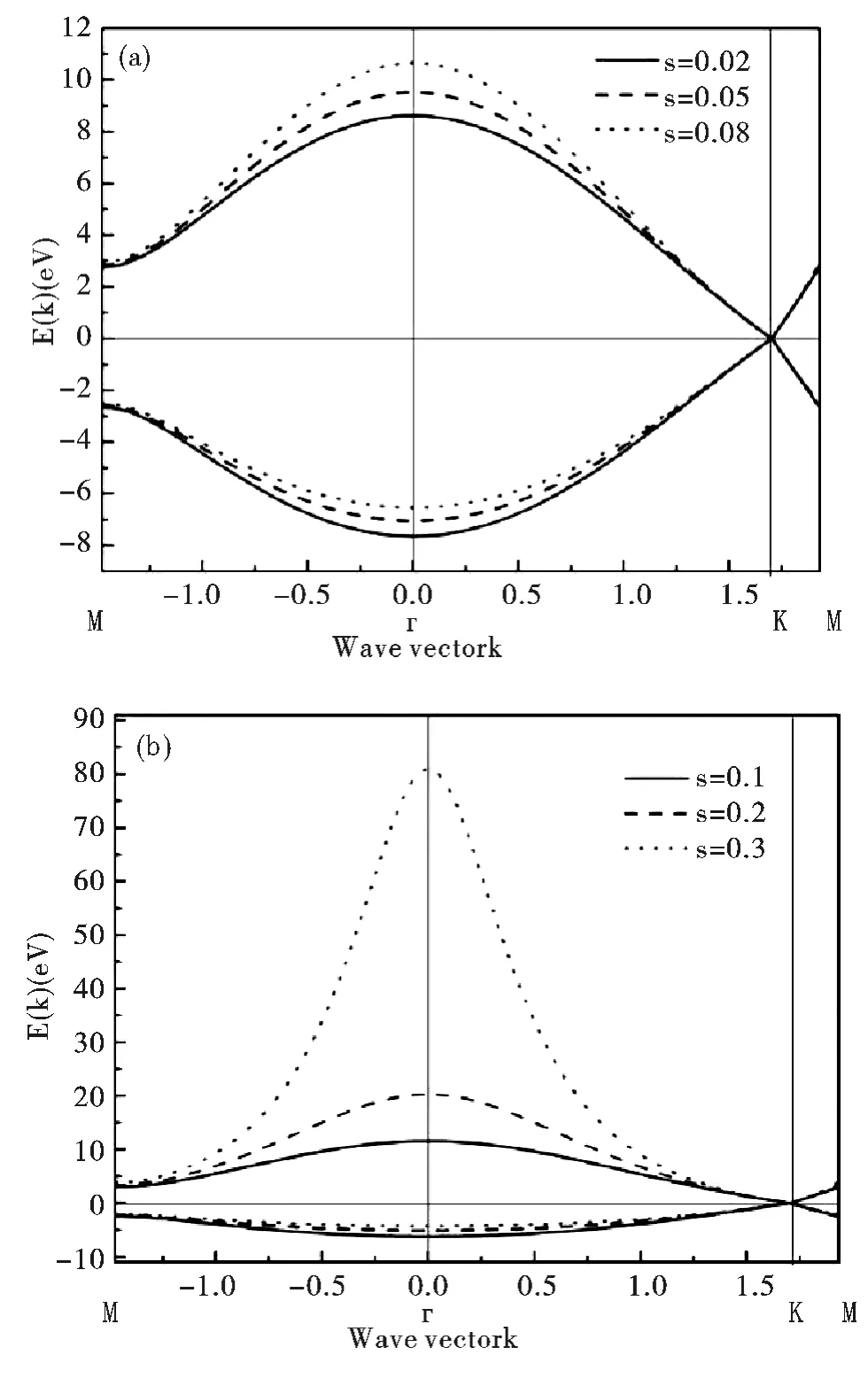
圖3 重疊矩陣在不同參數范圍內對能量的影響:(a)s ＜0.1 ;(b)s ＞0.1Fig. 3 The energy band is affected by the overlap integral in different parameter:(a)s ＜0.1 ; (b)s ＞0.1

3.2 能態密度

圖5 為計算所得的石墨烯的能態密度(DOS)ρ( )ε . 從圖中可知，能態密度在費米面(對應Dirac 點)ε = 0 處，為零;在Dirac 點附近呈線性變化，這不同于一維和二維材料的能態密度變 化. 在ε = ± 2.7eV (- 點)，即ε = ±|V_ pppi| ，能態密度無窮大，此時電子的速度很小. 在ε = ± 2.7eV 左右，能態密度越來越小，但在ε ≤| V_ pppi| 范圍內，變化急劇;在| V_ pppi|≤ε ≤3 | V_ pppi| 范圍內，能態密度也越來越小，但是變化較為平緩，Γ 點的DOS 為0.2042.

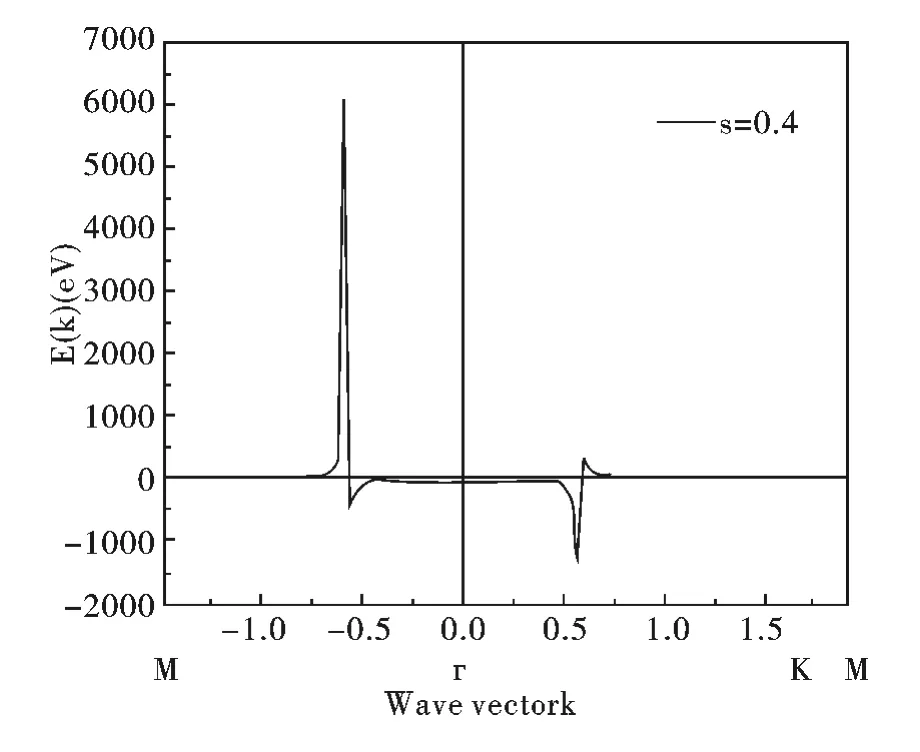
圖4 能帶隨波矢在s=0.4 時的變化圖Fig. 4 The energy band as a function of wave vector k for s=0.4

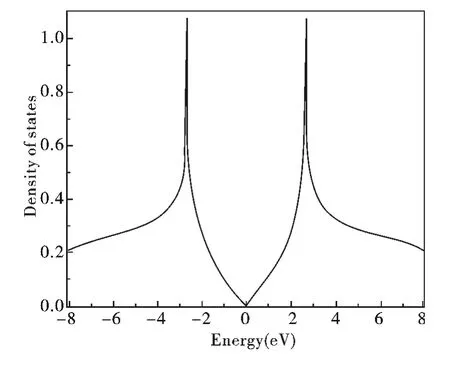
圖5 石墨烯的能態密度(Density of States)Fig. 5 The density of states of graphene

4 結 論

本文使用了緊束縛勢方法對石墨烯的能帶進行了研究. 正交基矢下的π 能帶具有完全對稱性，考慮軌道重疊后，對稱性受到破壞，重疊效應使價帶靠近費米面，而使導帶遠離費米面. 軌道重疊s 越小，導帶越靠近費米面，而價帶越遠離費米面，取值在s≤0.1 范圍內能保持原子在實際空間中重疊所引起的能帶的改變，太大則會導致物理上失效(s=0.4). 石墨烯的能態密度ρ( )ε 在費米面(對應Dirac 點)ε = 0 處，為零;在Dirac 點附近呈線性變化. 在-點，能態密度無窮大，此時電子的速度很小. Γ 點的能態密度為0.2042.

附錄:

［1］ Novoselov K S，Geim A K，Morozov S V，et al. Electric field effect in atomically thin carbon film［J］. Science，2004，306 (5696):666.

［2］ Lin Y M，Dimitrakopoulos C，Jenkins K A，et al. 100-GHz transistors from wafer-scale epitaxial graphene［J］. Science，2010，327(5966):662.

［3］ Geim A K，Novoselov K S. The rise of graphene［J］.Nat. Mater.，2007，6:183.

［4］ Appelhans D J，Lin Z B，Lusk M T. Two-dimensional carbon semiconductor:Density functional theory calculations［J］. Phys. Rev. B，2010，82:073410.

［5］ Konschuh S，Gmitra M，Fabian J. Tight-binding theory of the spin-orbit coupling in graphene［J］. Phys.Rev. B，2010，82:245412.

［6］ Harrison W A. New tight-binding parameters for covalent solids obtained using Louie peripheral states［J］.Phys. Rev. B，1981，24(10):5835.

［7］ Reich S，Maultzsch J，and Thomsen C. Tight-binding description of graphene［J］. Phys. Rev. B，2002，66:035412.

［8］ Castro Neto A H，Guinea F，Peres N M R，et al. The electronic properties of graphene［J］. Rev. Mod.Phys.，2009，81(1):109.