一類離散MIMO系統的神經網絡自適應輸出反饋容錯控制

劉　磊，　王占山

一類離散MIMO系統的神經網絡自適應輸出反饋容錯控制

劉磊，王占山

（東北大學信息科學與工程學院，沈陽110819）

針對一類離散多輸入多輸出（MIMO）嚴格反饋系統，提出了基于神經網絡的輸出反饋容錯控制.由于討論的執行器故障類型有失效和卡死兩種情況，提出了比例驅動方法，可將這兩種故障類型恰當地表示出并便于控制器的設計；同時，由于此類多輸入多輸出系統不滿足匹配條件，通過引入預測控制設計方法，可以克服這一缺陷.考慮到系統中的函數是未知的，利用神經網絡具有逼近任意連續函數到任意精度的原理來估計該未知函數，由此證明了本文所提出的方法可以使得系統的所有參數及實際容錯控制律均一致最終有界.通過MATLAB實驗仿真，有效地驗證了此方法的合理性.

容錯控制；執行器故障；多輸入多輸出離散系統；神經網絡；輸出反饋控制

動態系統的容錯控制（Fault Tolerant Control，FTC）是伴隨著基于解析冗余的故障診斷技術的發展而發展起來的.針對非線性連續系統的容錯控制已有許多成果［1-4］，諸如單輸入單輸出（SISO）系統［5］、多輸入單輸出（MISO）系統［6］、多輸入多輸出（MIMO）系統［7］等.隨著互聯網及計算機演算的發展，離散系統比連續系統更能描述實際的控制系統［8］，因為電腦的運算往往會用到采樣技術.目前，針對非線性離散系統的容錯控制也已成為熱點，并取得了一些研究成果［9-12］.但是，這些在離散系統中的容錯控制方法，都是在狀態反饋的基礎上建立的.

基于輸出反饋的離散系統的控制理論已得到人們的廣泛研究［13-16］.文獻［13］中，針對帶有服務質量約束的網絡控制系統，提出了基于輸出反饋的鎮定化控制器.文獻［14］中，基于網絡化的運動系統，一種改進的魯棒靜態輸出反饋PID控制策略被提出.然而，這兩種輸出反饋的控制方法，均需要滿足匹配條件，即系統的未知動態必須與控制信號在一個通道里面.文獻［16］中，針對不滿足匹配條件的離散系統，靈活運用預測控制方法，提出了一種基于未知方向的輸出反饋神經網絡控制方法.另外，當系統的執行器發生故障時，系統的正常運行將受到影響，這些方法均不能直接有效地控制系統.

綜上所述，本文針對一類離散MIMO系統，考慮執行器卡死或者失效的情況，提出了一種基于神經網絡的自適應輸出反饋容錯控制器.由于故障類型有兩種，采用比例驅動法，將這兩種故障類型表示成一種凸組合的形式，便于容錯控制器的設計.同時，由于控制信道之外，仍然含有未知函數，利用神經網絡具有萬能逼近的原理來估計該未知函數.通過仿真實驗，證明了所提容錯控制方法的有效性.

1　系統描述及預備知識

考慮如下含有執行器故障的多輸入多輸出嚴格反饋離散系統

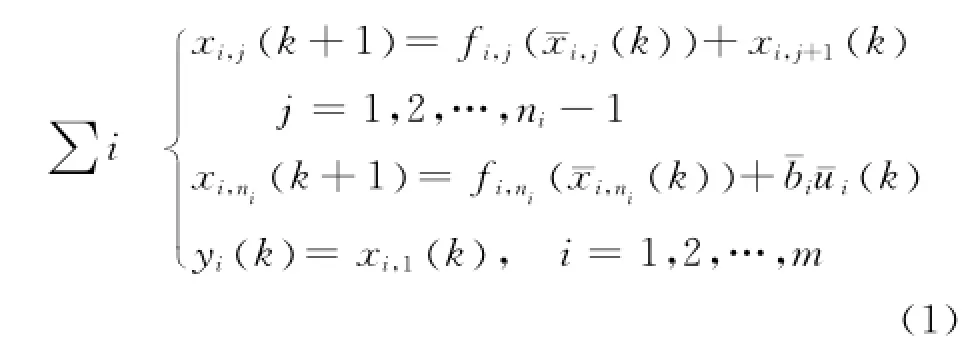
本文所考慮的執行器故障包括卡死和失效兩種類型，具體表示為：

卡死

其中：u^ip表示第i個子系統中第p個執行器卡死；kip是卡死時間.即若一個執行器卡死，其相應的輸入值就不變了.

失效

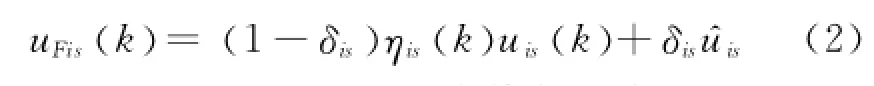
式中，若第i個子系統中第s個執行器卡死，則δis= 1，否則δis=0.

為了方便容錯控制器的設計，有如下假設.

假設1第i個子系統里的執行器最多有li-1個是卡死故障，即至少有一個執行器是失效故障.在此情況下，假設系統仍能運行.

假設2期望輸出yd（）k∈Ωy，k＞0是已知光滑的，Ωy是有界緊集.

控制目標設計一個基于神經網絡的輸出反饋容錯控制律，使得每個子系統的輸出yi（k）盡可能地跟蹤上指定的期望軌跡，并且系統的所有信號均一致最終有界.

2　容錯控制器設計

根據文獻［15］中的方法，可將系統進行坐標變換，變換結果如下：

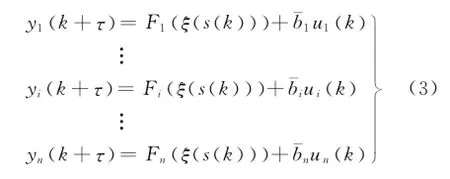
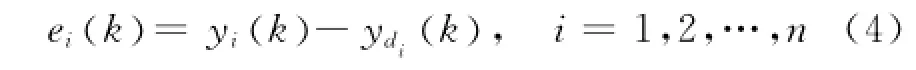
于是，可得誤差動態方程為

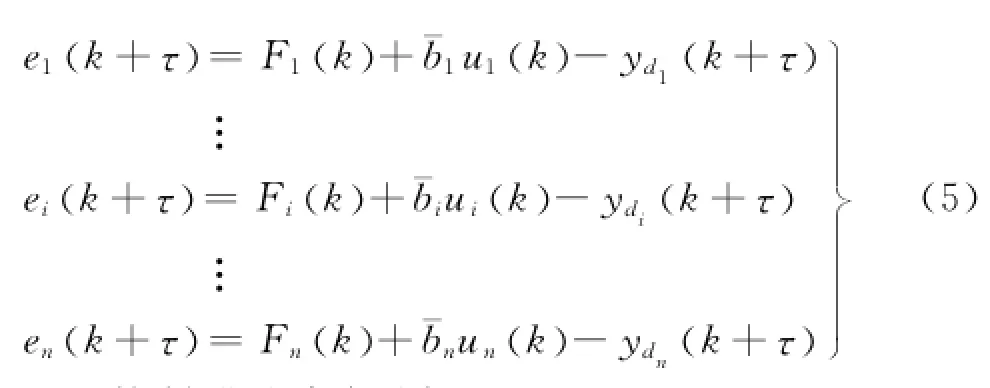
控制器設計步驟如下：

第1步由式中第一個式子，運用文獻［5］中提出的比例驅動法，可得和分別的下界和上界.因此有

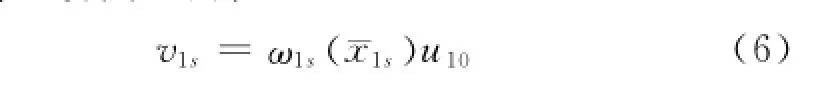
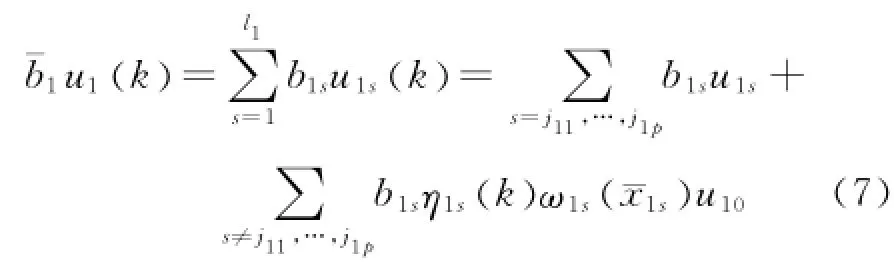
選擇理想控制器

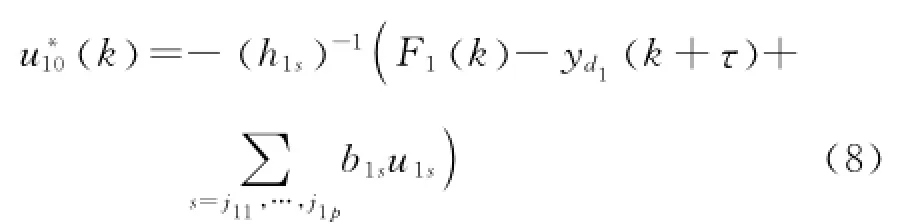
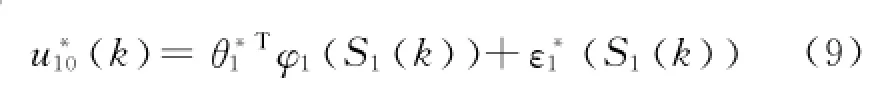
式中：θ1是神經網絡最優權重；是徑向基函是最優逼近誤差；S1（k）=.于是可選擇如下控制輸入和自適應律：

運用類似如上設計方法設計控制器：

第i步由式中第i個式子，選擇理想控制器

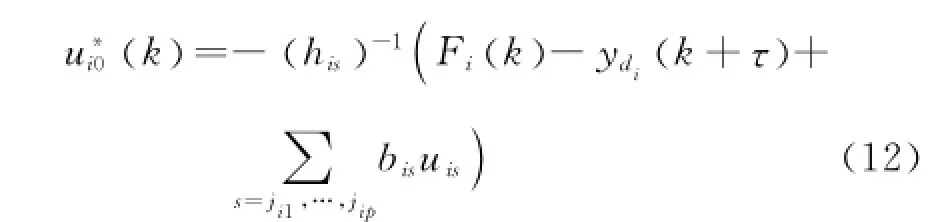
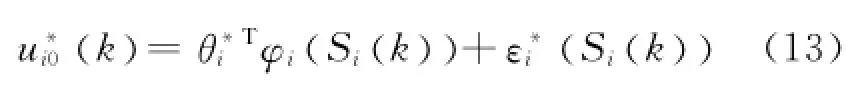
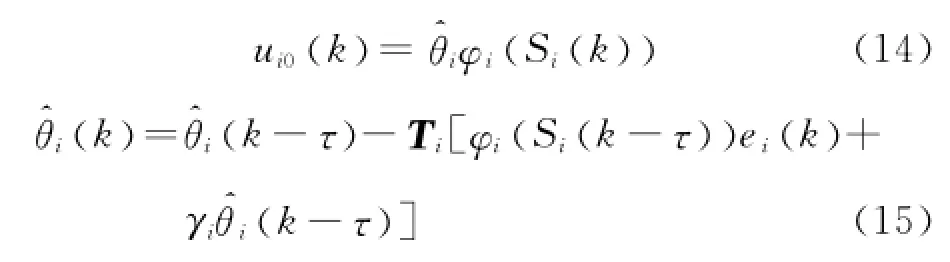
定理1考慮一類帶有執行器故障（如式（2）的MIMO離散系統（如式（1）），基于假設1和2，設計自適應律如式（11）和（15）所示，提出自適應容錯控制器如式（10）和（14）所示，則該MIMO離散系統的所有信號均一致最終有界.

證明

第1步由式（5）和（7），可知可得

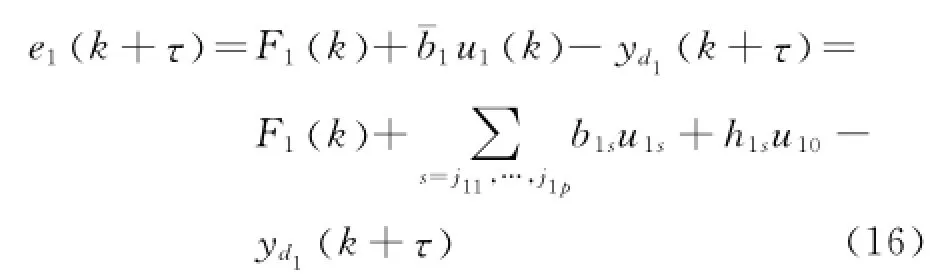
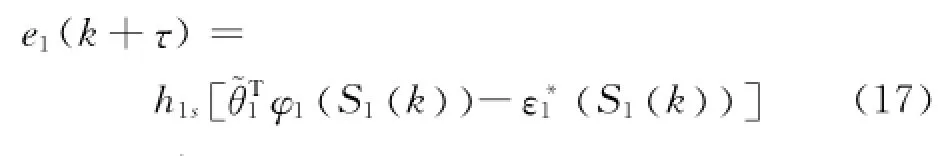
式中，~θT1=θ^T1-θT1是神經網絡權重估計誤差.

選取如下李雅普諾夫函數

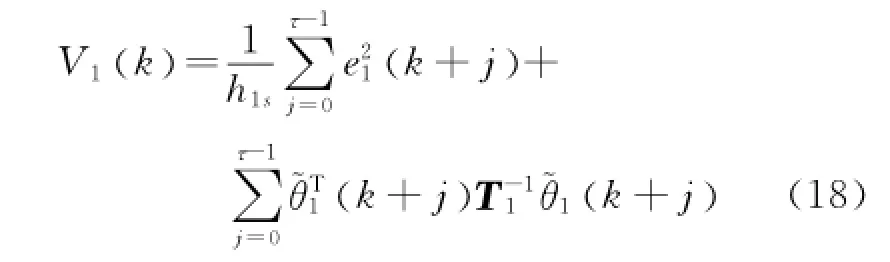
由式（11）和（16），可得

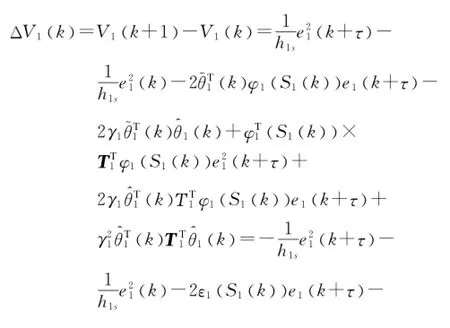
考慮如下不等式：

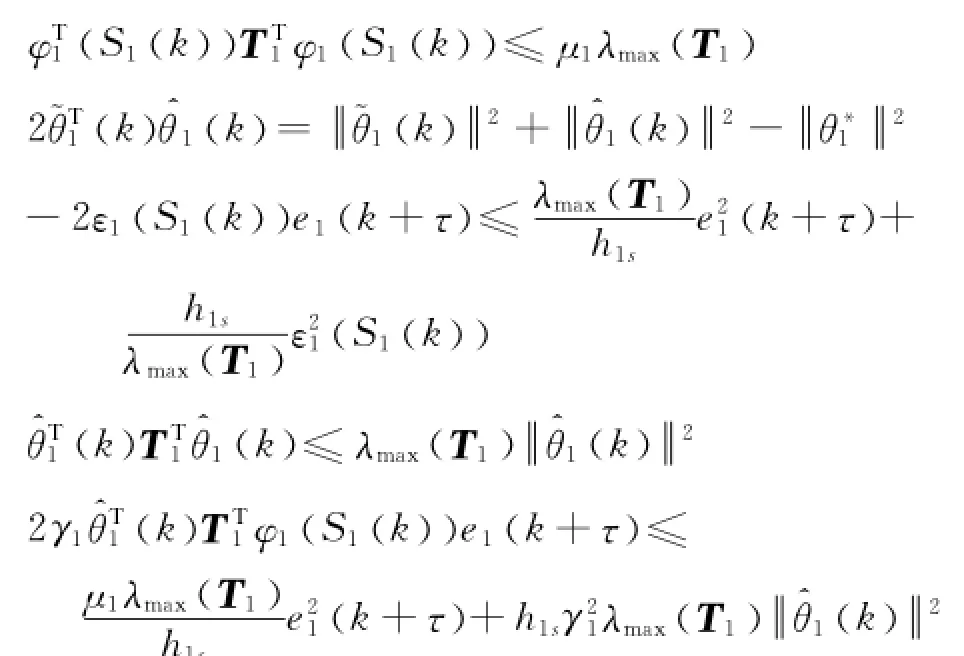
其中，μ1是神經網絡節點數，λmax（Τ1）是Τ1的最大特征值.

因此，有

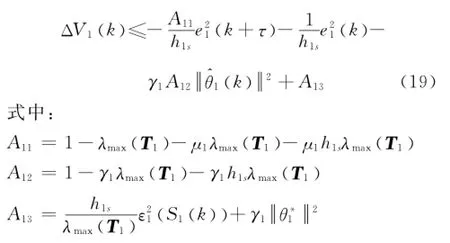
若設計參數λmax（Τ1）和γ1滿足如下條件：

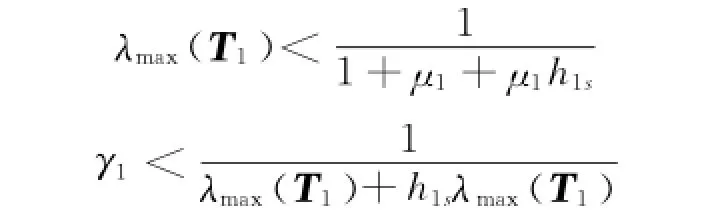
則式（19）可寫為

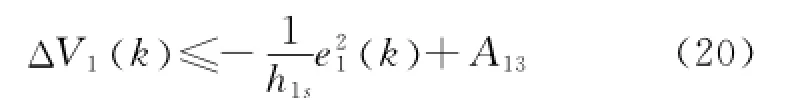
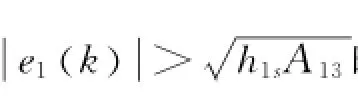
第i（i=2，3，…，n）步選取如下李雅普諾夫函數

應當說，毛主席的心情可以理解，他的希望也不是沒有道理。但《紅燈記》是按事物內在發展邏輯、系統而完整的文藝創作，如果改變其中的重要人物命運，會使作品傷了元氣，失去悲劇的應有力量。所以，閆肅沒有改，堅持了自己的尺度，之后多年的演出效果，也證明他是對的。

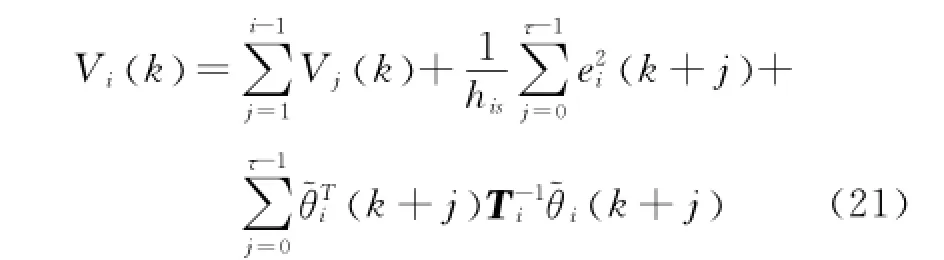
進行與第1步相同的過程，可得

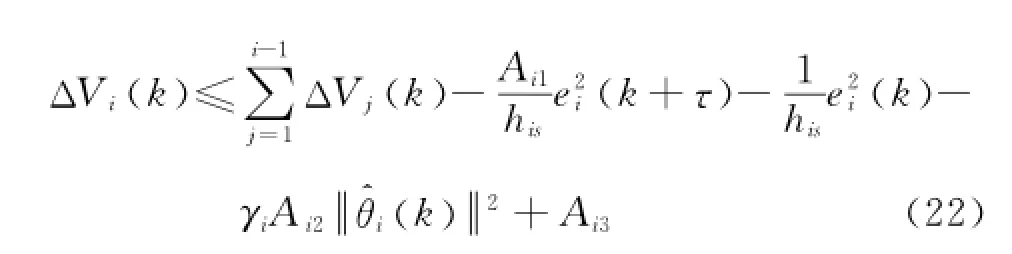
式中：

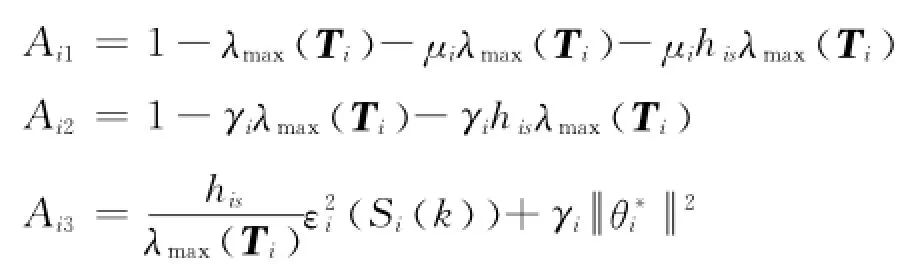
若設計參數λmax（Τi）和γi滿足如下條件：

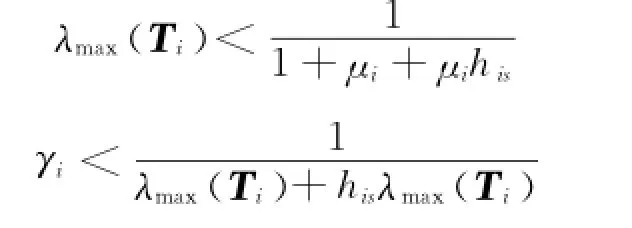
則式（22）可寫為

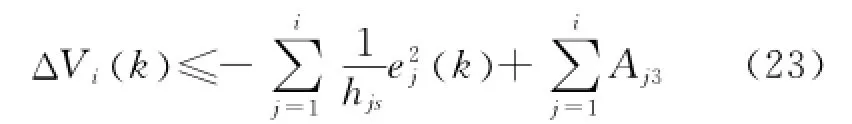
綜上所述，對于閉環非線性多輸入多輸出系統式（1），若選擇滿足如下條件的設計參數：

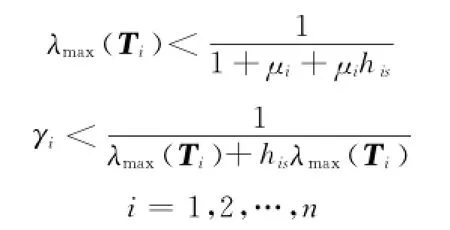
3　仿　真

考慮如下MIMO離散系統［14］：

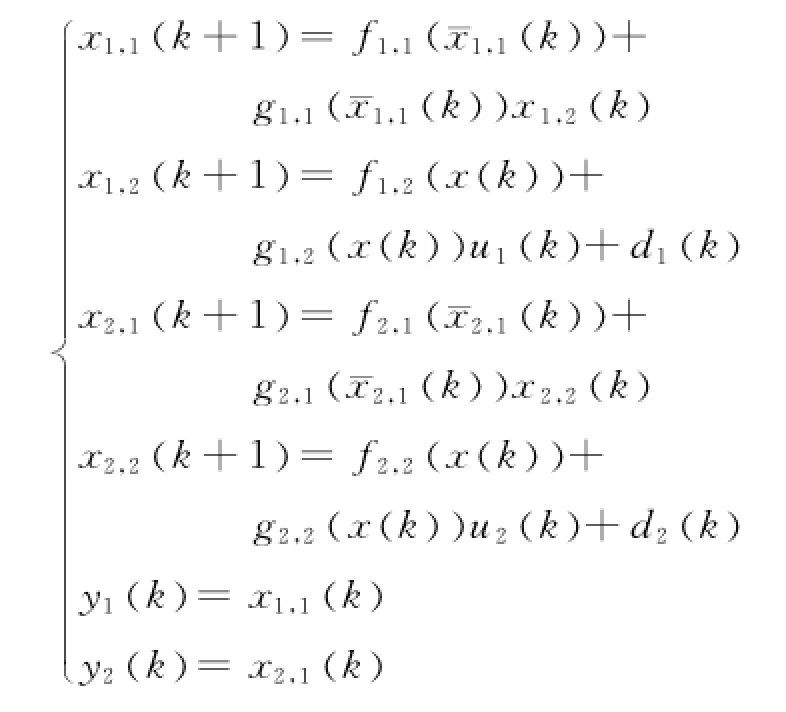
其中：

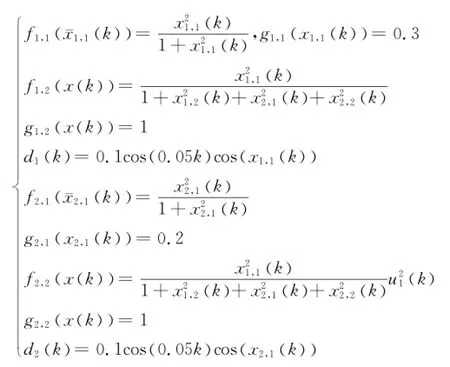
期望輸出信號為：

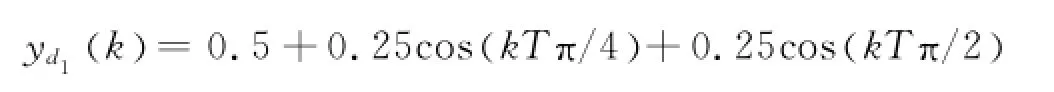
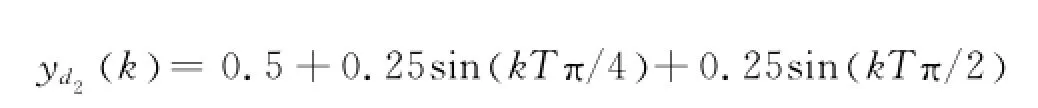
仿真結果如圖1所示.圖1（a）為第1個子系統的跟蹤效果.由圖可見，即使執行器失效，其跟蹤效果仍然良好.圖1（b）為第2個子系統的跟蹤效果.當系統發生卡死故障時，系統的跟蹤效果有短暫的影響，但隨后，跟蹤誤差也在“零”的小鄰域內.

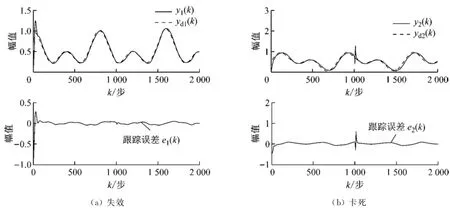
圖1　不同故障狀況下系統跟蹤性能及跟蹤誤差Fig.1　The tracking performances and tracking errors under different fault

4　結　語

本文建立的基于神經網絡的容錯控制器通過輸出反饋方式給出.被考慮的離散系統不再是SISO

系統，而是擴充到MIMO系統.不僅考慮了執行器的卡死故障，也考慮了執行器的失效故障.通過比例驅動法，便于容錯控制的設計.由于MIMO離散系統包含未知函數，利用徑向基神經網絡可以有效地估計該未知函數.因系統不滿足匹配條件，引進預測控制方法，可有效地解決這一問題.最后，通過李雅普諾夫穩定性分析法，證明了閉環系統中的所有信號均一致最終有界.

［1］姜斌，冒澤慧，楊浩，等.控制系統的故障診斷與故障調節［M］.北京：國防工業出版社，2009.

［2］王占山，張化光.一類自適應觀測器的故障估計性能［J］.東北大學學報：自然科學版，2004，25（12）：1134-1137.

［3］Wang Z，Li T，Zhang H.Fault tolerant synchronization for a class of complex interconnected neural networks with delay［J］.International Journal of Adaptive Control and Signal Processing，2014，28 （10）：859-881.

［4］Wang Z，Zhang H.Design of a bilinear fault detection observer for singular bilinear systems［J］. Journal of Control Theory and Applications，2007，5 （1）：28-36.

［5］Wang W，Wen C.Adaptive actuators fault compensation for uncertain nonlinear systems with guaranteed transient performance［J］.Automatica，2010，46（12）：2082-2091.

［6］Tang X，Tao G，Joshi S.Adaptive actuator faultcompensation for nonlinear MIMO systems with an aircraft control application［J］.Automatica，2007，43 （11）：1869-1883.

［7］Liu L，Wang Z，Zhang H.Adaptive NN faulttolerant control for discrete-time systems in triangular forms with actuator fault［J］.Neurocomputing，2015，152：209-221.

［8］Mahmoud M.Stochastic stability and stabilization for discrete time fault tolerant control system with state delays［C］／／American Control Conference.Seattle，USA：American Automatic Control Council，2008：1040-1045.

［9］Jiang B，Zhang K，Shi P.Integrated fault estimation and accommodation design for discrete-time Takagi-Sugeno fuzzy systems with actuator faults［J］.IEEE Trans Fuzzy Syst，2011，19（2）：291-304.

［10］Thumati B，Feinstein M，Sarangapani J.A modelbased fault detection and prognostics scheme for Takagi-Sugeno fuzzy systems［J］.IEEE Transactions on Fuzzy Systems，2014，22（4）：736-748.

［11］Zhang D，Yu L.Fault-tolerant control for discretetime switched linear systems with time-varying delay and actuator saturation［J］.Journal of Optimization Theory and Applications，2012，153（1）：157-176.

［12］Peng C，Tian Y C，Yue D.Output feedback control of discrete-time systems in networked environments ［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A：Systems and Humans，2011，41（1）：185-190.

［13］Zhang H，Shi Y，Mehr A S.Robust static output feedback control and remote PID design for networked motor systems［J］.IEEE Transactions on Industrial Electronics，2011，58（12）：5396-5405.

［14］Zhang J，Ge SS，Lee T H.Output feedback control of a class of discrete MIMO nonlinear systems with triangular form inputs［J］.IEEE Transactions on Neural Networks，2005，16（6）：1491-1503.

［15］Yang C，Ge S S，Xiang C，et al.Output feedback NN control for two classes of discrete-time systems with unknown control directions in a unified approach ［J］.IEEE Transactions on Neural Networks，2008，19（11）：1873-1886.

［16］Wang Z，Zhang H，Li S.Robust fault diagnosis for a class of nonlinear systems with time delay［J］. Journal of Harbin Institute of Technology：New Series，2007，14（6）：884-888.

（編輯俞紅衛）

NN-Based Adaptive Output Feedback Fault Tolerant Control for MlMO DiscreteTime Systems

LIU Lei，WANG Zhanshan
（School of Information Science and Engineering，Northeastern University，Shenyang 110819，China）

In view of a class of MIMO discrete-time systems，a neural network（NN）-based output feedback fault tolerant control（FTC）was presented.On account of the considered actuator faults containing both of loss of effectiveness and lock-in-place，the proportional-actuation method was utilized to combine the two fault types into a proper expression to design the FTC conveniently.Meanwhile，due to the failure of the MIMO systems in satisfaction with the matching condition，this restriction could be solved by bringing in predictive control technique.Based on the NNs’approximate ability of estimating any function to arbitrary precision，the unknown system function was approximated by using NNs.Then，it’s proved that all the signals and the fault-tolerant controller in the closed-loop systems were uniform ultimate boundedness（UUB）.A MATLAB simulation showed the effectiveness of the proposed FTC approach.

fault tolerant control（FTC）；actuator fault；MIMO discrete-time systems；neural networks （NN）；output feedback control

TP 306.3

A

1671-7333（2015）03-0293-06

10.3969／j.issn.1671-7333.2015.03.016

2015-01-15

國家自然科學基金資助項目（61473070，61433004）；中央高校基本科研業務費資助項目（N130504002，N140406001，N130104001）；流程工業綜合自動化國家重點實驗室資助項目（2013ZCX01）

劉磊（1987-），男，博士生，主要研究方向為基于神經網絡的大規模系統的故障檢測、容錯控制.E-mail：liuleill＠live.cn

王占山（1971-），男，教授，博士生導師，主要研究方向為非線性控制系統的故障診斷、容錯控制方法及其在工業過程中的應用，神經網絡系統理論及其應用.E-mail：zhanshan_wang＠163.com