頁巖儲層的改進拉鏈式壓裂裂縫間距優化

艾　池，高長龍，李玉偉，徐　樂，劉亞珍，張　軍（．東北石油大學石油工程學院，黑龍江大慶6338；．遼河油田鉆采工藝研究院，遼寧盤錦400）

頁巖儲層的改進拉鏈式壓裂裂縫間距優化

艾池1，高長龍1，李玉偉1，徐樂2，劉亞珍1，張軍1
（1．東北石油大學石油工程學院，黑龍江大慶163318；2．遼河油田鉆采工藝研究院，遼寧盤錦124010）①

針對改進拉鏈式壓裂優化設計的要求，在假設巖石為均質、各向同性材料的基礎上，建立誘導應力計算模型，得出近井地帶最大誘導應力差計算公式及最佳裂縫間距表達式，確定了中間裂縫最佳起裂位置，并建立多裂縫縫間誘導應力差計算模型。研究表明：隨著泊松比的增加，誘導應力差最大值減小，縫間最佳間距增大；隨著縫內壓力的增加，誘導應力差最大值增大，縫間最佳間距不變；裂縫高度增加，誘導應力差最大值不變，縫間最佳間距增加；當裂縫間距增加時，近井地帶誘導應力差先增大后減小，井間裂縫交匯處的誘導應力差逐漸減小，誘導應力差值分布趨于均勻化。進行壓裂設計時，在滿足裂縫轉向條件的前提下，可根據實際情況適當擴大縫間距離，增加遠場裂縫網絡的復雜性，提高改造體積。

頁巖；改進拉鏈式壓裂；間距優化

頁巖儲層孔隙度及滲透率較低［1-2］，要實現頁巖氣的有效開采，必須提高儲層滲透率，目前國內外所采取的改造手段主要是以提高改造體積為目標的體積縫網壓裂技術［3-5］，主要包括同步壓裂、交替壓裂和改進拉鏈式壓裂［6，7］，但同步壓裂的改造體積比較有限，且井間竄流風險高，而交替壓裂容易引起近井地帶應力轉向，形成縱向裂縫，導致油氣井砂堵，而改進拉鏈式壓裂能夠克服以上兩種壓裂方式的不足，并能夠在井間形成較為充分的裂縫網絡，達到提高采收率的目的。

國內外在誘導應力場分布規律及裂縫轉向機理方面研究較為成熟［8-10］，但在裂縫間距優化方面研究較少，程萬等［11］分析了原始地應力場及裂縫半長等因素對裂縫間距的影響，邵尚奇等［12］對不同裂縫間距下的誘導應力分布規律進行了研究，尹建等［13］利用誘導應力計算模型對射孔間距進行了實例計算，本文針對改進式拉鏈壓裂裂縫間距設計進行分析，通過建立多裂縫縫間誘導應力差計算模型，確定先壓開兩條裂縫的最佳間距及中間裂縫最佳起裂位置，并對不同裂縫參數、不同泊松比及縫內凈壓力下誘導應力差值的分布規律進行研究，在考慮避免近井地帶形成縱向裂縫，防止砂堵及井間竄流的發生的基礎上，對裂縫最佳間距的設計原則進行了研究。

1　多裂縫誘導應力差計算模型

采用Palmer擬三維裂縫數學模型，建立如圖1所示的坐標系，假設裂縫的垂直剖面為橢圓形，縫長方向為x軸，縫高方向為y軸，坐標軸原點位于裂縫中心，可得出裂縫垂直剖面上的半縫高h為［14］：

式中：hp為儲層厚度的一半，m；ld為裂縫半縫長，m；hd為井底最大半縫高，m。

根據式（1）變形可得出裂縫垂直剖面上的半縫高h為：

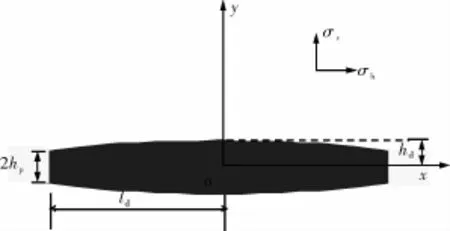
圖1　裂縫垂向剖面圖

圖2為裂縫縫高剖面示意圖，其中縫寬方向與最小主應力方向相同，為z軸方向，縫高方向與垂向地應力方向相同，為y軸方向。

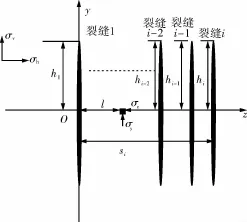
圖2　裂縫縫高剖面示意

設拉應力為正，壓應力為負，則可以得到任意一條水力裂縫在z，y平面內某質點（l，0）處產生的各方向誘導應力大小為［14-17］：

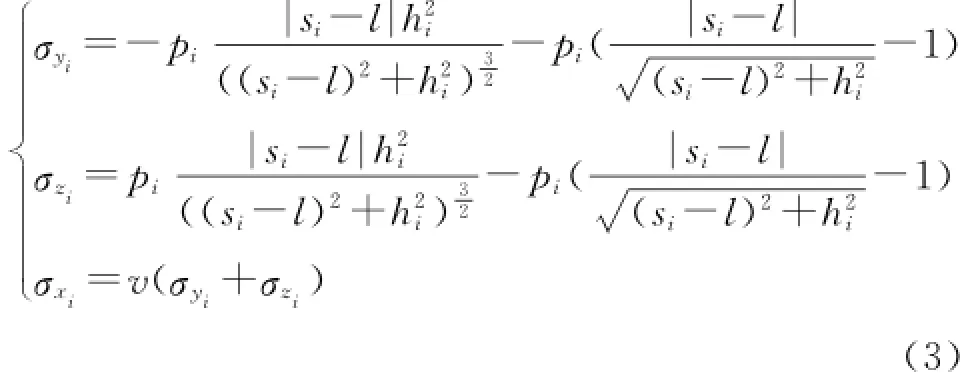
式中：σxi，σyi，σzi分別為形成的第i條裂縫所產生誘導應力在x，y，z方向的正應力分量，MPa；pi為縫內凈壓力，MPa；si為第i條裂縫與第1條裂縫間的距離，m；l為z軸上一點與裂縫中心的距離，m；hi為第i條裂縫的半縫高，m；v為地層泊松比。

則水平誘導應力差值為：

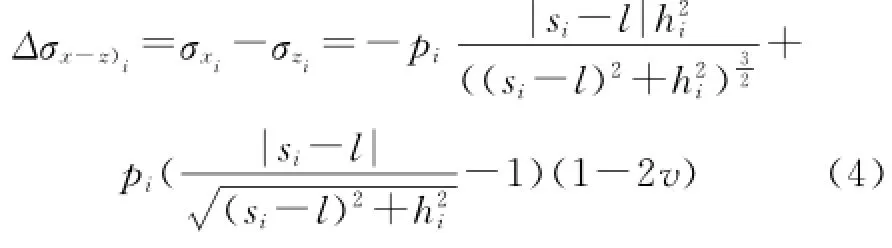
對式（4）求導，可得到裂縫i產生的水平誘導應力差最大值點與裂縫i的距離li：

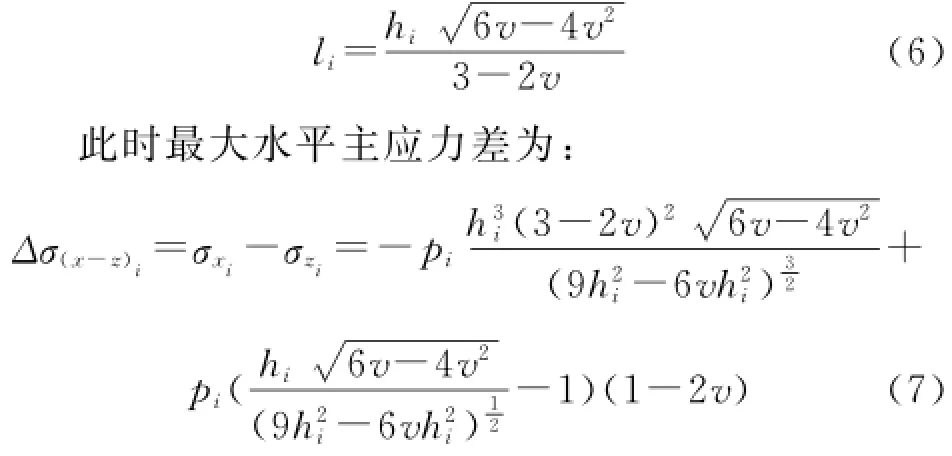
由式（6）可計算縫間最佳間距，即當i裂縫水平誘導應力差均達最大時，裂縫水平誘導應力差最大點與裂縫間的距離的關系式分別為：

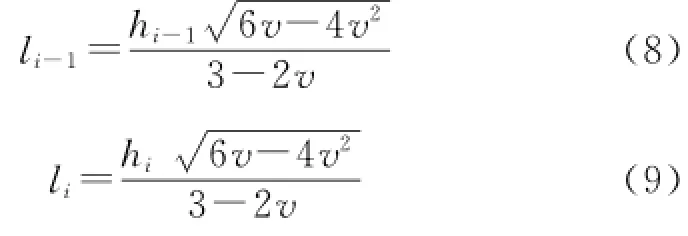
式中：li－1和li分別為裂縫i－1和裂縫i水平誘導應力差最大值點與裂縫間距離，m；hi－1和hi分別為裂縫i－1和裂縫i的半縫高，m。

由上述分析可得，當2條裂縫之間的距離為li－1＋li時，縫間水平誘導應力差值最大，主裂縫周圍的分支裂縫容易發生轉向，形成裂縫網絡，由式（8）～（9），可得裂縫縫間最佳間距為：

中間裂縫最佳起裂位置為距第i條裂縫與第i－1條裂縫距離之比（li∶li－1）或縫高之比（hi∶hi－1）處，可利用式（2）與（6）進行計算。

聯立式（4）與式（6）得出近井地帶縫間最大誘導應力差計算公式為：

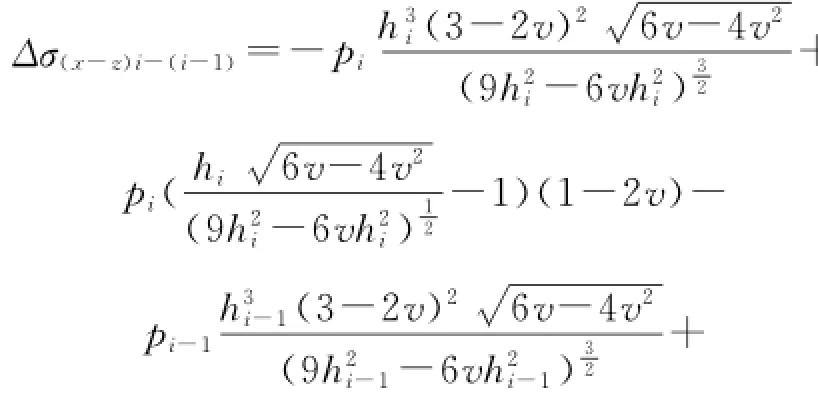
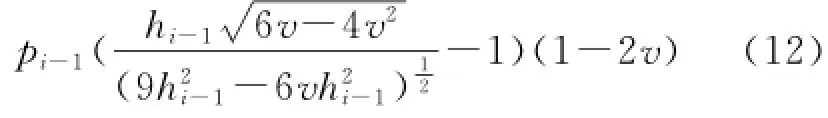
井間裂縫交匯處與井筒平行方向上任意一點（l，0）的處的誘導應力差計算公式為：

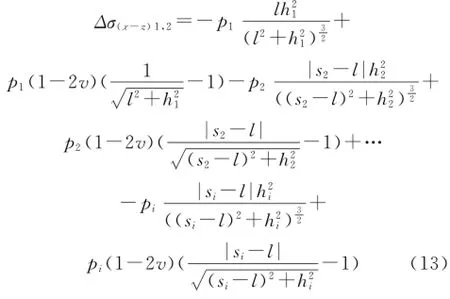
在進行拉鏈式壓裂設計時，可依據式（12）與（13）計算近井地帶誘導應力差及井間裂縫交匯處的誘導應力差。

2　實例分析

以某油田頁巖儲層兩口改進拉鏈式壓裂水平井為例進行數值計算。兩口井間距離326m，油層厚度18．00m，泊松比0．23，最大水平主應力－37．80 MPa，最小水平主應力－30．80 MPa，上覆巖層壓力－34．80 MPa，縫內凈壓力－5 MPa，井底最大半縫高均為43．00m，裂縫半長均為180．00m；利用式（2）計算可以得出裂縫形態如圖3。

圖3　裂縫形態

當裂縫長度和最大半縫高及油層厚度確定時，利用式（2）可以計算裂縫任意點處的縫高，分別計算了x＝179．030m處的半縫高10m、x＝162．954m處半縫高20m、x＝131．876m處半縫高30m及x＝67．551m處半縫高40m的誘導應力差及中間裂縫最佳起裂位置的變化規律（如圖4～5）。

由圖4～5可以看出裂縫附近誘導應力差隨裂縫間距離的增加，呈現先增加后減小的趨勢，誘導應力差存在最大值點，其數值大小不受縫高影響，縫高越大，最佳縫間距越大且中間裂縫最佳起裂位置與兩側裂縫間的距離越大。

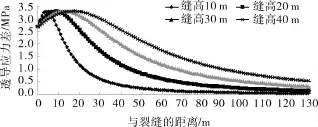
圖4　不同縫高處誘導應力差

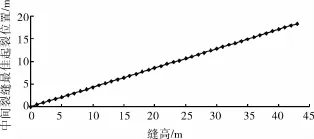
圖5 縫高對中間裂縫起裂位置的影響

計算得出裂縫中心軸線上，不同泊松比及縫內凈壓力條件下誘導應力差和中間裂縫起裂位置的變化（如圖6～8）。

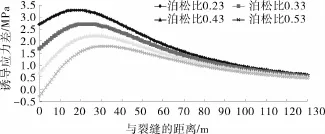
圖6　泊松比對誘導應力差的影響

圖7　泊松比對中間裂縫起裂位置的影響

由圖6～7可以看出隨著泊松比的增加，誘導應力差最大值逐漸減小，誘導應力差值最大值點與裂縫的距離逐漸增加，最佳縫間距增加且中間裂縫最佳起裂位置與兩側裂縫間的距離也增加。

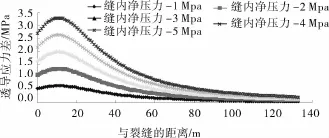
圖8　不同縫內凈壓力條件下誘導應力差的變化

由圖8中可以看出縫內凈壓力并不影響誘導應力最大差值點與裂縫間的距離，但縫內凈壓力越大，誘導應力最大值差越大，但最佳縫間距及中間裂縫最佳起裂位置均不發生變化。

在改進拉鏈式壓裂施工過程中，首先壓開裂縫1及裂縫3，然后在合適位置壓開裂縫2（如圖9）。

圖9　改進拉鏈式壓裂示意

根據式（11）可知裂縫1與2及裂縫2與3之間的間距應滿足比例1∶1，在此條件下改變裂縫間距，得出近井地帶及井間裂縫交匯處誘導應力差分布，如圖10～11所示。

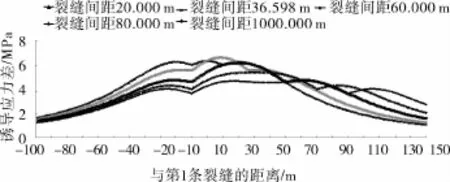
圖10　近井地帶誘導應力差分布

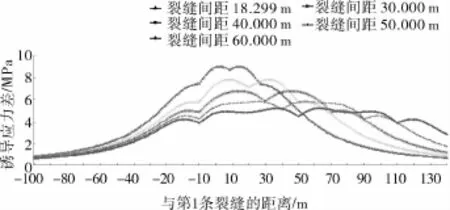
圖11　井間裂縫交匯處的誘導應力差分布

比較近井地帶和井間裂縫交匯處誘導應力差分布可以看出，近井地帶與井間裂縫交匯處誘導應力差存在峰值及拐點，拐點為裂縫的位置，峰值為誘導應力差最大值點；在近井地帶，裂縫間距在0～36．598m（最佳間距）區間變化時，隨著縫間距的增加，裂縫1與裂縫3之間的誘導應力差逐漸增加，峰值擴張，縫間距大于36．598m后，隨著縫間距的增加，裂縫1與裂縫3之間的誘導應力差逐漸減小，峰值收縮。但隨著裂縫間距的增加，裂縫3左側誘導應力差逐漸減小，而裂縫1右側誘導應力差逐漸增加，整體誘導應力差分布趨于均勻化；在井間裂縫交匯處，隨著裂縫間距的增加，裂縫3左側及裂縫1、2、3之間區域的誘導應力差逐漸減小，峰值收縮，但裂縫1右側誘導應力差逐漸增加，誘導應力場分布趨于均勻化。本文計算實例初始水平應力差為7MPa，裂縫1與3最優間距為36．598m，此間距井間裂縫交匯處所產生的誘導應力差最大值為9．068MPa＞7MPa，可形成轉向裂縫，且此間距下近井地帶最大誘導應力差為6．601MPa＜7MPa。因此在本實例計算中縫1與裂縫3最佳間距為36．598m，裂縫2的起裂位置與兩側裂縫的距離為18．299m，但對于初始水平應力差較小的儲層，保證裂縫轉向的前提下，應盡量擴大裂縫間距，以增加裂縫轉向區長度，提高改造體積。

3　結論

1） 裂縫附近誘導應力差值隨著與裂縫距離的增加，變化趨勢先上升后下降，且上升較快，下降較慢，存在最大值點，其最大值隨著縫內凈壓力的增加而增加，隨泊松比的增加而減小，不受縫高的影響。

2） 中間裂縫最佳起裂位置和縫間最佳間距不受縫內凈壓力的影響；但隨著泊松比和縫高的增加，最佳縫間距增加且中間裂縫最佳起裂位置與兩側裂縫間的距離增加。

3） 對于拉鏈式壓裂設計，其中間裂縫最佳起裂位置為兩條裂縫最大誘導應力差值點交匯處，在近井地帶，裂縫間距在0至最佳間距之間變化時，隨著裂縫間距的增加，裂縫間誘導應力差值逐漸增加，裂縫間距超出最佳間距后，誘導應力差值隨著裂縫間距的增加逐漸減小，而在井間裂縫交匯處，隨著裂縫間距離的增加誘導應力差逐漸減小。實際施工中，可根據本文計算模型結合現場實際情況，在保證井間交匯處裂縫轉向的前提下，適當增大裂縫間距，提高改造體積，避免近井地帶發生應力轉向形成縱向裂縫，增加遠場裂縫網絡復雜性。

［1］ 董大忠，鄒才能，楊樺，等．中國頁巖氣勘探開發進展與發展前景［J］．石油學報，2012（S1）：107-114．

［2］ 羅鐘鳴．壓裂斜井時射孔處雁形裂縫產生及干擾分析［J］．石油礦場機械，2005，34（3）：11-14．

［3］ 朱正喜，曹會，陳沙沙．國內水力噴射壓裂工藝技術應用研究進展［J］．石油礦場機械，2014，43（12）：82-87．

［4］ 李小剛，蘇洲，楊兆中，等．頁巖氣儲層體積縫網壓裂技術新進展［J］．石油天然氣學報，2014（7）：154-159．

［5］ 王學正，韓永亮，王海霞，等．側鉆水平井分段壓裂完井技術在氣田的應用［J］．石油礦場機械，2014，43（12）：44-47．

［6］ East L E，Soliman M Y，Augustine J R．Methods for enhancing far-field complexity in fracturing operations ［R］．SPE133380，2010．

［7］ Rafiee M，Soliman M Y，Pirayesh E．Hydraulic fractu-ring design and optimization：amodification to zipper frac［R］．SPE159786，2012．

［8］ 陳勉．頁巖氣儲層水力裂縫轉向擴展機制［J］．中國石油大學學報（自然科學版），2013（5）：88-94．

［9］ Green A E，Sneddon I N．The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid［J］．Mathematical Proceedings of the Cambridge Philosophical Society，1950，46（1）：159-163．

［10］ Zhao H F，Chen H；Liu G H；New insight intomecha-nisms of fracture network generation in shale gas res-ervoir［J］．Journal of Petroleum Science and Engi-neering，2013（110）：193-198．

［11］ 程萬，金衍，陳勉，等．頁巖儲層水平井分段壓裂裂縫間距設計方法及影響因素分析［J］．科學技術與工程，2014（15）：43-46．

［12］ 邵尚奇，田守嶒，李根生，等．水平井縫網壓裂裂縫間距的優化［J］．石油鉆探技術，2014（1）：86-90．

［13］ 尹建，郭建春，曾凡輝．水平井分段壓裂射孔間距優化方法［J］．石油鉆探技術，2012（5）：67-71．

［14］ 李玉偉，艾池，張博文，等．同步體積壓裂對井間裂縫特性的影響［J］．斷塊油氣田，2013（6）：779-782．

［15］ 劉洪，胡永全，趙金洲，等．重復壓裂氣井誘導應力場模擬研究［J］．巖石力學與工程學報，2004（23）：4022-4027．

［16］ 翁定為，姚飛，李陽，等．重復壓裂裂縫轉向時油藏數值模擬研究［J］．石油鉆采工藝，2006（6）：65-67．

［17］ 張公社，趙蓓，石惠寧，等．重復壓裂裂縫轉向的AN-SYS有限元模擬［J］．石油天然氣學報，2009（6）：141-144．

Optimization of Fracture Spacing of Shale Reservoir Acquired by Improved Zipper Type Fracturing

AI Chi1，GAO Changlong1，LI Yuwei1，XU Le2，LIU Yazhen1，ZHANG Jun1
（1．College of Petroleum Engineering，Northeast Petroleum University，Daqing 163318，China；2．Drilling&Production Technology Research Institute，Liaohe Oilfield，Panjin 124010，China）

According to the requirement of the improved zipper type fracturing optimization and de-sign，assuming that the rock is homogeneous and isotropic，the calculationmodel of induced stress is established，obtaining the calculationmodel ofmaximum difference of induced stress around the wellbore and the expression of the optimum fracture spacing，ascertaining the optimum fracture initiation position of intermediate base cracks，and then the calculationmodel of difference of in-duced stress amongmultiple fractures is established．Researches show that as Poisson ratio in-creases，themaximum value of induced stress difference decreases and the optimum spacing among fractures increases；as the pressure of fracture increases，themaximum value of induced stress difference increases and the optimum spacing among fractures is invariant．However，as the frac-ture height increases，themaximum value of induced stress difference is invariant and the opti-mum spacing among fractures increases；as the fracture spacing increases，the induced stress difference around the wellbore firstly increases and then increases，and the induced stress of the line intersection of inter-well fracture gradually decreases，and the induced stress difference seemsdistribute evenly．For fracturing design，on the premise of fracture reorientation，we the fracture spacing can be appropriately enlarge according to practical situation，and increase the complexity of fracture network in far-field，and improve volume．

shale；improved zipper type of fracture；spacing optimization

TE934．201

A

10．3969／j．issn．1001-3842．2015．08．005

1001－3482（2015）08－0021－05

①2015－01－13

國家自然科學基金“基于混沌理論煤層氣井壓裂孔裂隙分形演化與滲流特征研究”（51274067）

艾 池（1957-），男，黑龍江大慶人，博士，教授，博士生導師，主要從事油氣井工程力學、油水井增產增注方面研究，Email：aichi2001＠163．com。