基于Ad Hoc 網絡通信協定協議研究

楊誠，詹永照

基于Ad Hoc 網絡通信協定協議研究

楊誠，詹永照

Ad Hoc網絡的關鍵技術是路由技術，對網絡整體性能產生著最重要的影響，針對Ad Hoc網絡動態變化的拓撲結構，原有固定網絡中的路由協議已經能滿足其需要，要求必須對新的Ad Hoc路由協議進行設計。基于Ad Hoc網絡的基本概念，以雙線性對和層次路由協議為基礎，提出ad hoc網絡中通信有效的密鑰協定協議，對應邏輯密鑰協定模型與實際網絡拓撲結構，使建立和動態更新初始群密鑰得到了支持，具有較小的通信量。實驗和性能分析后得知，針對有較大的范圍、較強的設備處理能力，而較差的通信環境而言，提出的協議效果非常好。

Ad hoc 網絡；密鑰協定；層次路由；雙線性對

0 引言

為了使有線網絡對人們的束縛得以擺脫，渴望自由通信能夠隨時隨地進行，我國最近幾年開始大力發展無線網絡通信[1]。移動中的通信能夠借助便攜計算機或個人數字助理（配有無線接口）來實現[2]。不過只有在有線基礎設施（如基站）的支持下方能實現移動通信[3]。基于將通信帶進沒有固定基站的地方，出現了Ad Hoc網絡技術。網絡節點移動性很強是Ad hoc網絡的特點，存在非常脆弱的成員關系與無線鏈路，所以必須重視安全通信[4]。一般來說，安全的密鑰是保證網絡安全的重要手段，所以就要重視對會話密鑰的安全進行研究[5]。不過針對實際的應用，通常這些協議都會分離密鑰協定模型與實際的網絡拓撲結構，從而其有效性與安全性就有可能出現問題，也就不太適合ad hoc網絡[6]。

要提高ad hoc網絡中密鑰協定協議的效率，就要使通信量得以降低，方法有二：（1）基于對ad hoc網絡層次路由（Hierarchy Routing）技術的運用，分簇處理網絡，達到基本一致的密鑰分配邏輯結構和實際網絡拓撲結構，密鑰樹的相鄰結點盡量選用實際網絡中的相鄰點，從而使單播問題得以最大程度的避免，使單播問題帶來的不穩定性和復雜性得以削弱，從根本上使協議的通信復雜度得以降低。（2）基于對雙線性映射額利用，再改進RSTR(改進的STR)協議，進一步降低其通信量，從而在具有較大范圍、較強節點處理能力并在較大網絡延遲的環境中適用，像軍事與緊急救助等場合。

1 Ad Hoc網絡的一般加密算法

在應用了各種類型的加密算法后，從而有可能實現認證性、完整性、安全性與機密性，對稱加密算法、單向Hash函數、非對稱加密算法與數字簽名是主要的幾種加密算法。

（1）對稱加密算法

針對密鑰的使用，發送者與接收者都一樣，從而說明雙方對信息的加密與解密都可以使用這一密鑰。相對簡單、較短的密鑰長度是對稱加密算法的特點，所以，可以快速運算，對產生極大消耗的CPU資源進行加密操作，對大數據量的信息進行加密，對稱加密算法是非常適用的，有助于對信息安全提供極大的保護。不過換言之，因為二者需要在協商的基礎上對一個秘密密鑰進行共享使用，從而二者其一就有可能會泄露密鑰。

同時，若相互通信的人有n個，就會有n-1個秘密密鑰保存在每個人手中，則需要對n*（n-1）/2的密鑰數目進行管理，管理這么多的密鑰有一定的難度，同時，怎樣向相應的信息獲取者安全地傳遞密鑰也是一大難題。DES、AES、CAS、3DES、IDEA與CAST等是比較流行的對稱加密算法。

（2）非對稱加密算法

在加密明文時，采用的密鑰是一對，而且各不相同，包括個人私有的私鑰和對外公開的公鑰。二者性質非常特殊，也就是只有用對應的公鑰才能解開私鑰加密的密文，私鑰不具備解密的功能，反過來也是這個道理。

一些很難解決的數學問題決定了非對稱加密算法的安全性，諸如對兩個大素數的乘積進行分解、對離散對數問題求解、對橢圓離散對數問題求解等，以現有的計算機水平來解決這些難題，即便將公鑰得到也沒有辦法將相應的私鑰推出。在非對稱加密算法性質良好的基礎上，從而在網絡安全系統中得到了廣泛的應用。不過由于其具有較長的密鑰和很慢的運算速度，所以，只是在較小數據量的情況下比較適用。

同時，偽裝攻擊容易光顧非對稱加密算法，也就是中間人（man in the Middle）攻擊：若密鑰交換正在A與B之間進行，這時介入交換的是第三個人C，初始的公共值本由A向B發送，這時C進行了攔截，進而另一個公共值由C發送到B，然后C又攔截了B發給A的消息，但是B卻不知道這一切，從而一個共享密鑰的協議在A與C之間達成，并且另一個共享密鑰的協議在B與C之間達成，所以，A到B的消息就被C在中間攔截了，進而對A與C共享的密鑰解密進行操作，對消息內容進行修改，接著基于對B與C共享密鑰的使用，向B進行轉發；相反的，B發給A的消息過程也被C篡改，但是A與B并不知情。RSA、EIGamal、Diffie-Hellman與Ecc等是比較流行的非對稱加密算法。

（3）Hash函數

用某一固定長度“消息摘要”（Message Digest）對任意長度的消息進行壓縮需要借助Hash函數，不同于對稱加密算法與非對稱加密算法，逆向運算是Hash函數做不到的，密鑰也不需要。無法進行逆向運算就是Hash函數安全性的所在，也就是單向的算法，“摘要”能夠被用戶從原文得到，但是，原文卻無法從“摘要”得到，所以，以“摘要”作為信息就能夠安全的在網上傳送。除此之外，消息原文不一樣，被同一個Hash函數運算后，也會得到不同的結果，所以Hash函數有助于完整性檢驗。MD5與SHA等是比較流行的Hash函數。

（4）數字簽名—數字簽名（Digital signature）

作為一個加密的消息摘要，在一個文檔后面附加的數字簽名—數字簽名，基于非對稱加密算法與Hash函數的組合完成了對它的建立，能夠在發送者身份與文檔完整性的確認中使用。消息內容的機密性并不能得到數字簽名的保證，不過有時，對消息來源進行證明要重要于隱藏消息的內容。有些時候，消息的認證性與完整性是需要的，機密性卻不需要，就像路由更新信息在網絡上傳遞的時候，加密是并不需要的，不過是否可信的路由更新的來源是需要確認的。此處我們再舉一個例子來說么消息來源認證的重要性，針對電子商務與銀行事務，必須重視并認真對事務的來源進行確認，是對任何事務采取行動前必須要做的。RSA數字簽名算法與數字簽名標準DSS是最常用的一些數字簽名算法。NIST提出了基于非對稱加密算法的DSS。

相比RSA，針對密鑰的生成，DSS具有更快的速度，二者性能基本相同，不過具有很慢的簽名驗證速度。當前階段，針對最終用戶或設備認證的建立，非對稱加密技術往往是許多安全系統的首選，公鑰的分發要遵循某種安全的方式，就像借助數字證書，數字簽名的創建采用Hash函數，同時，證書內數據的完整性必須確保。一般通過某種加密算法來保證數據的機密性。對數據與業務流量機密性進行提供的同時，也可以部分或全部地用于其它安全機制的實現，在網絡安全中最重要的部分就是密碼技術。

2 CEKAP協議設計

以單跳原則為基礎，CEKAP協議分簇網絡都能通過單跳到達簇中的任意節點。借鑒文獻[1]，文章利用兩個過程對密鑰進行協定：建立初始群密鑰與構造邏輯群密鑰樹，通過IKA（Initial Key Agreement）過程完成；加入與移除初始群密鑰建立后的網絡節點等事件，通過AKA（Auxiliary Key Agreement）來完成。網絡邏輯結構體現為邏輯群密鑰樹，不一定完全對應網絡的物理結構，群密鑰樹的構造基于IKA過程對分簇信息的利用。

2.1 參數設置和邏輯密鑰樹

假定加法群表示為G1，乘法群表示為G2，素數q是二者的階，G1的生成元表示為P，雙線性映射用ê：G1×G2→G2表示，Hash函數用H：G2→Z表示，能在Z中映射G2上的元素。CEKAP協議的邏輯群密鑰樹如圖1所示：

圖1 CEKAP協議的邏輯密鑰樹

群密鑰樹由簇密鑰樹與主干密鑰樹組成。簇密鑰樹用虛線橢圓標出，葉子節點表示實際網絡節點，以小圓表示，簇頭是實心圓，添加的虛擬節點用于建樹表示為空心方形。各個簇密鑰樹由主干密鑰樹連接，實心方框表示其節點，節點也是虛擬的。

因為網絡節點與葉子節點相對應，為了方便敘述，文章用一個概念表示二者。全部節點編號采用三元組〈c, l, v〉，節點所屬簇號表示為c；在簇c中從底向上節點所處層號表示為；節點在c簇l層按照從左至右的順序的順序號表示為v，1為簇密鑰樹中 c、 l、v取值的開始，c=0（主干密鑰樹中）。如A的編號為〈1, 1, 1〉，B的編號為〈6, 2, 3〉。c簇 l層的全部節點表示為〈c, l, *〉，一層的代理表示層中v最大的節點，用S〈c, l 〉表示；c簇的全部節點表示為〈c, *, *〉，這一簇的代理表示為簇中〈c, l-1, *〉層的代理，用S〈c, l 〉表示。該層與下層密鑰的更新由層代理負責，簇的密鑰的更新由簇代理負責。

簇密鑰樹中的虛擬節點表示為〈c, l, 1〉（l〉1），在l層〈c, l-1, *〉層的代理的提升是其實際。主干密鑰樹中的虛擬節點表示我〈0, l, 1〉，在主干密鑰樹中所轄的最后一個簇的代理的提升是其實際。c簇第l層的節點數（含內部節點）表示為#(c, l )，{1, 2, 3}為其取值。每一隨機秘密值r〈c, l, v〉都會對應一個葉子節點。c簇l層以下全部葉子節點協定的密鑰值表示為k〈c, l〉，公開給這些葉子節點，不過保密于其它節點。c簇全部節點協定的簇密鑰表示為kc，公開給c簇，保密于其它簇。

最終的群密鑰用K表示，kc以至K的值都可以通過每個葉子節點自己的隨機秘密值與該節點到根節點路徑上相鄰節點的隨機值的某種形式求出。例如節點〈1, 1, 1〉用r〈1, 1, 1〉,r〈1, 1, 2〉P , r〈1, 1, 3〉P可以算出k〈1, 2〉；利用k〈1, 2〉，r〈1, 2, 2〉P,r〈1,2,3〉P可以算出k1；再利用k1，k2P，k3P，k4P，k5P，e?(P,P)可以算出K。因為G2中的元素之一為e?(P,P)，當密鑰需要多方協定時借助H在Z中映射它。假定共有節點n個，rk (k=1,…,n)是節點k的秘密值，令α=(P,P)，則協定后的群密鑰

K形如：

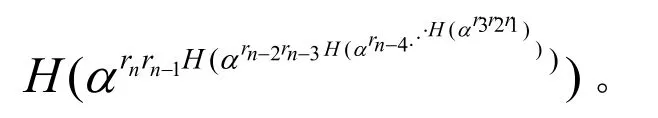
2.2 基本密鑰協定協議

若4大于協定密鑰的節點數，則通過下面兩個基本協議對密鑰進行協定。

基本協議1 ：基于對定理2的運用，在A、B、C3個成員間將密鑰協定：

A→B,C： aP，A選擇秘密值a，廣播aP ；

B→A,C： bP，B選擇秘密值b，廣播bP；

C→A,B： cP，C選擇秘密值c，廣播cP ；

最終A，B，C可計算出k = ê(P, P) abc

基本協議2 ：基于對推論2的運用，在A，B間將密鑰協定：

A→B：ê(P, P)a，A選擇秘密值a，廣播ê(P, P)a ；B→A：ê (P, P)b，B選擇秘密值b，廣播ê(P, P)b ；最終A，B可計算出k = ê(P, P) ab

2.3 初始群密鑰協定過程

設協定過程中存在暫時固定的網絡拓撲結構，網絡節點數為N ≥ 2，簇Ci共有m個，每個簇的網絡節點數為ni，小組gj(1≤i≤m; 1≤j≤hi)共有hi=[(ni-1)/2]個，用#(gj)表示小組gj的節點數，#(g1)=3或2，#(ghi)=2或1，#(gu)=2（1〈u〈hi），小組代理由每個小組的最后一個節點代表，表示為S〈i, j〉，協調與其它組的通信事務。我們通過兩個步驟對群密鑰進行協定：

（1）簇密鑰協定。

小組密鑰的協定由每個簇的gi組完成，接下來以基本協議為依據S〈i,j-1〉和gi組的成員共同完成該小組密鑰k〈i,j〉（1≤i≤m; 1〈j≤hi）的協定，k〈i,j－1〉是此時S〈i,j-1〉選擇的隨機秘密值，也就是j-1及以下層密鑰的協定值。最后k〈i,hi〉即為簇密鑰ki。能夠在全部簇中并行執行簇密鑰的協定，以使簇密鑰的生成時間得以減少。

以簇密鑰生成過程為依據，密鑰樹的一層就是每個小組，葉子節點就是組成員，連接借助虛擬節點實現，能夠最終完成邏輯簇密鑰樹的構造。針對簇密鑰樹，到樹根路徑上相鄰節點的隨機值r的某種形式（節點數為3，就是rP，否則為(P,P)r）每個節點都知道，簇密鑰可以被每個葉子節點計算出來。在一個簇中，簇的代理并不一定是簇頭，簇頭負責響應網絡節點的加入和移除，通知簇的代理發生了網絡拓撲結構的變化，由代理引發密鑰更新過程。

（2）群密鑰協定。

生成群密鑰由簇代理代表該簇參與，網絡節點就是每個簇，一個簇就是整個網絡，以協定簇密鑰類似方法為依據協定群密鑰，進而完成群密鑰樹的構造，到樹根結點路徑上相鄰節點的隨機值r的某種形式的值（為rP或e?(P,P)r）每個節點都知道，群密鑰K能夠被每個葉子節點計算出來。

2.4 群密鑰更新過程

節點具有較強的移動性和不穩定的網絡拓撲結構是ad hoc網絡的特點，要保證簇密鑰的安全，必須對節點的變化進行跟蹤并適時地對簇密鑰進行更新。簇頭節點負責對網絡分簇變化的響應，向簇代理進行通知并對簇密鑰進行更新，最終對群密鑰進行更新，群密鑰更新由下面7種事件引發。

（1）單節點加入（Join）

若在網絡中加入節點V，以層次路由協議為依據，在簇Ci中加入該節點，V加入事件的響應由簇頭作出，同時向該簇的代理通知，與V共同更新簇密鑰，設用hi個小組對簇Ci進行劃分，為使下標得以簡化， 讓hi=n ，則情況如下：

（a）若2=#(gn)，在加入V后將其劃分到第n組，簇密鑰樹的高度不增加，以基本協議1為依據，在〈i, n, 1〉、〈i, n, 2〉和V間對簇密鑰ki進行更新，以下是其過程：

〈i, n, 1〉給〈i, n, 2〉及V單播 ：k〈i,n-1〉P ；

〈i, n, 2〉廣播 ：r〈i,n,2〉’P，即S〈i,n〉換一個秘密隨機值r〈i,n,2〉’，給〈i, *, *〉廣播r〈i,n,2〉’P ；

V廣播 ：rvP，給〈i, *, *〉廣播rvP。

（b）若3=#(gn)那么在加入V后將劃分到第n＋1組，1是簇密鑰樹高度的增加值。以基本協議2為依據更新密鑰，以下為其過程：

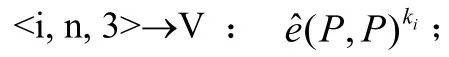
進而以（7）為依據，群密鑰更新過程由簇Ci發起。

（2）單節點移除（Remove）

設〈i, l, v〉為移除的成員，V移除事件的響應由Ci的簇頭作出，同時向S〈i,l〉通知更新簇密鑰，設用hi個小組對簇Ci進行劃分，讓 hi=n ，情況如下：

（a）如果1〈 l ≤ n，且#(gl)=3，則〈i, l, 2〉成為新的層代理S。一個新的隨機秘密值r'由S選擇，求得

〈i,l〉〈i,l,2〉〈i,l〉，接著將新的求出，廣播新的也能被其它成員計算出來。 若 #(g1)=2，那么的更新將由S〈i,l-1〉完成，將新的求出，接著將（t=1,...,n-1）廣播給其他成員。此時密鑰樹降低一層，即n=n-1。此時只需1次廣播消息。

（c）若將簇頭節點移除，就要重新劃分該簇，其實現由層次路由協議來完成，當簇被路由協議重新建好之后，進而以上述方式為依據來完成簇密鑰的更新。此外，設ad hoc網絡的群是動態對等的，具有相當的節點處理能力，因為能夠單跳到達一個簇中的節點，所以簇頭可以被簡單地指定為該簇中任一其它節點，以（a）或（b）的辦法為依據完成簇密鑰的更新[6]。

（3）多成員同時加入（Merge）

針對實際的應用，或許會有許多成員同時加入，其可能性有二：

（a）若是離散的成員，以(1)的做法為依據逐個加入。

（b）若一個簇由這些成員組成，那么以情況（5）為依據完成群密鑰的更新。

（4）多成員同時移除（Partition）

因為受到網絡故障的影響，或許會有許多成員同時離開。設〈i, l, v〉為其中對應簇密鑰樹層數最低的節點。若l 〉1，由l-1層的S〈i,l-1〉執行Delete操作；若l=1，由S〈i,2〉執行Delete操作。再按（7）更新群密鑰。

（5）簇的加入（Cluster Merge）

設在當前群中加入簇Ci，該簇要以IKA的辦法為依據將簇密鑰ki預先生成，接著與原群的代理共同以IKA中生成簇密鑰的方法為依據完成群密鑰的更新，同時將必要的消息廣播出去，以使新的群密鑰能被全部節點計算出來。此時群密鑰樹的最高層就是簇Ci，同時新的群代理也是簇Ci。

（6）簇的移除（Cluster Partition）

用一個網絡節點對應每個簇，一個簇對應整個網絡，該簇的移除采用類似于單節點移除的方法完成，同時將必要的消息廣播出去，以使新的群密鑰能被全部節點計算出來。

（7）密鑰更新（Key Agreement）

群密鑰的更新在上述（1）～（6）情況下都需要進行。都是通過某個簇Ci的代理觸發更新群密鑰。基于密鑰樹的角度，在更新過程中比Ci更低層的簇并不參與，只要將或廣播出去，新的群密鑰能被全部節點計算出來。

3 協議性能分析

3.1 通信量分析

（1）路由協議的通信量

不管底層的路由協議是否被密鑰協定方案考慮到，總會存在路由協議的通信開銷，如果可以借助對路由協議某些結果的利用服務密鑰協定方案，或許就會使密鑰協定協議的通信量得以降低。

基于4種動態情況，對比分析3種密鑰協定方案的通信量。如表1所示：

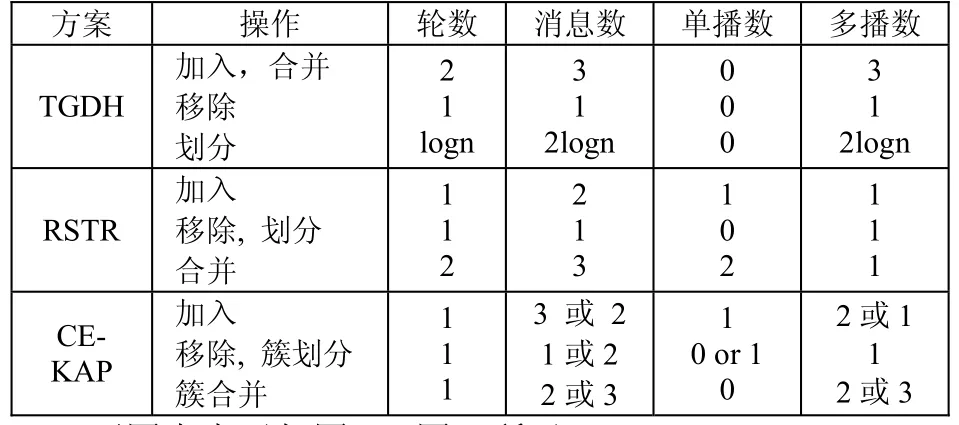
表1 CEKAP，TGDH和RSTR方案的通信量對比

畫圖表表示如圖2、圖3所示：

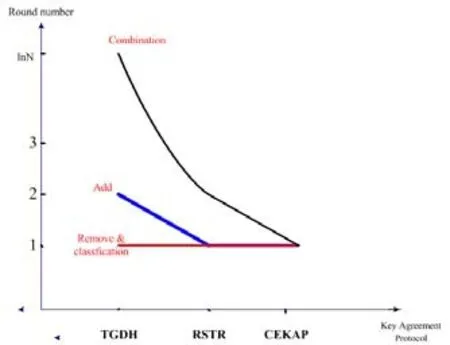
圖2 CEKAP，TGDH和RSTR方案的通信量對比

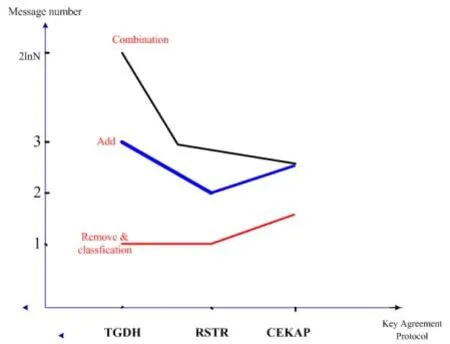
圖3 CEKAP，TGDH和RSTR方案的通信量對比

以事件響應層的節點數為3或2為依據，CEKAP協議取不同的消息數、單播和多播數，詳見表1所示。CEKAP方案有常量的輪數與消息數，基本相同于RSTR協議，并改進了“簇合并”方面的性能。同時，和TGDH協議相比，大大提升了“劃分”方面性能。但是，在分析TGDH和RSTR時，都沒有將單播的問題考慮進去，若設平均每次單播經過的轉發至少有1次，那么顯然性能更好的是CEKAP協議。所以降低路由協議與密鑰協定協議的通信量時，本方案有著更低的通信量。

3.2 計算量分析

標量乘（Scalar）、求對（Pairings）與模冪運算（Exponentiations）是基于BDH問題的密碼協議的計算量。對比操作AKA時CEKAP、TGDH與RSTR方案計算量，詳如表2所示：

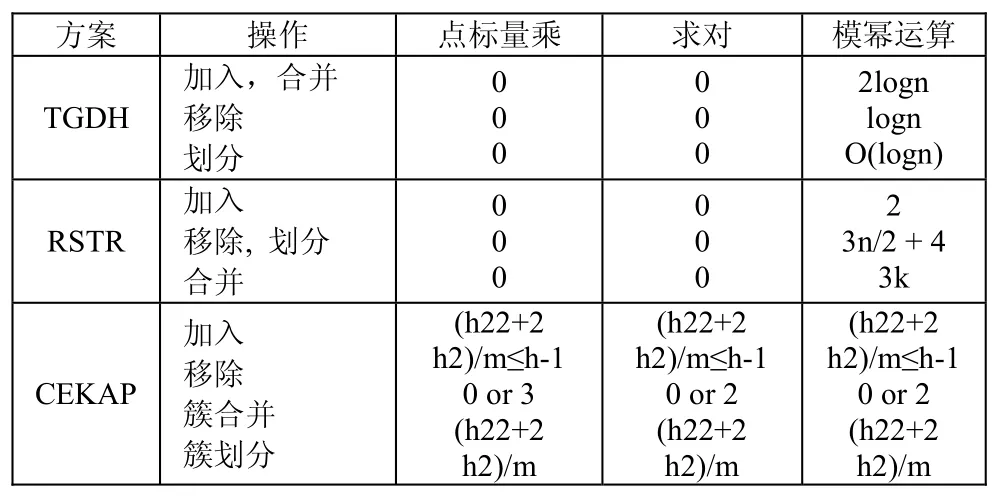
表2 CEKAP和TGDH，RSTR方案的計算量對比

畫圖表表示如圖4所示：

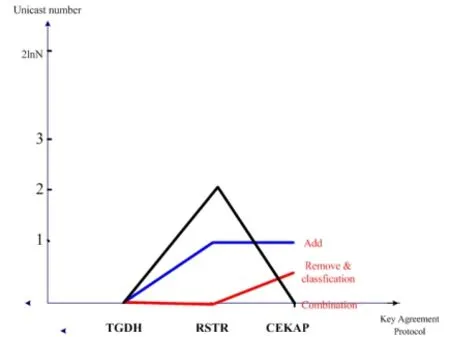
圖4 CEKAP和TGDH，RSTR方案的計算量對比

在表2中分析的是CEKAP的平均情況下的數據，從表2中可知，h、m、h2是影響CEKAP方案計算量的主要因素，也就是受群密鑰樹的高度、簇的數目、最大簇密鑰樹的高度及狀態改變的網絡節點的位置等的影響。操作“加入”與“簇劃分”計算量如圖5所示：

圖5 CEKAP和TGDH，RSTR方案的計算量對比

總的來說，正相關于m，越少的分簇，就會有越低的計算量。當次高層的結點數取值不同時，操作“簇合并”的計算量也不一樣，若取值為2，標量乘運算3次就可以；若取值為3，求對運算與模冪運算各2次，要優于TGDH與RSTR。

在表2中操作“移除”的計算量是最大的，其受h1，h2與移除節點的位置的影響，移除結點和樹根靠的越近，就會有越小的計算量。因為h1反比于h2，所以“移除”的計算量也會受到分簇方式的影響，使“加入”與“簇劃分”計算量得以降低的同時或許也會使它的計算量增大。

4 總結

文章以雙線性映射與ad hoc網絡中的層次路由協議為基礎，將一個密鑰協定協議CEKAP提出，獨立性較之以往密鑰更好，使前向與后向的安全得以同時保證。保證密碼是協議在安全性方面主要考慮的。與改進型STR方案的通信量基本相同，要優于TGDH，同時，因為是網絡都是單跳這一假定條件得以削弱，將會更好地應用到實際中去。Merge操作的計算量明顯優于TGDH與改進型STR方案，不過因為要對雙線性映射進行計算，基于雙線性對的密碼協議普遍存在的一個問題，也是CEKAP協議將會面臨的，從而處理某些操作時高于只需模冪運算的協議的計算量。在發現快速求對算法后，將會逐步改善這一問題。

[1]詹思瑜,李建平. 基于遺傳算法的Ad hoc路由協議優化[J]. 小型微型計算機系統,2012,01:24-27.

[2]劉靜,王賾. 可信鏈在Ad Hoc網絡的傳遞[J]. 計算機工程與應用, 2012,04:91-93+192.

[3]邵志毅,吳振強,馬亞蕾,王改寧. 一種Ad Hoc下的網絡編碼模型NCMA[J]. 計算機工程與應用,2012,04: 100-103,110.

[4]孫梅,趙兵. 基于身份的Ad Hoc網密鑰管理方案[J]. 計算機應用, 2012, 01:104-106+122.

[5]夏文潔,李千目,劉鳳玉,孫晉厚. 基于擬生滅過程的多跳Ad hoc網絡洪泛方式下擁塞控制及飽和條件研究[J].計算機科學, 2012,04:110-113.

[6]Mittra S.Iolus:A framework for scalable secure multicasting. In:ACM SIGCOM Computer Communication Review[J]. New York: ACM Press, 1997. 277-288.

Based on the Research of the Ad Hoc Network Protocol Agreement

Yang Cheng, Zhan Yongzhao
(Changzhou College of Information Technology, Changzhou 213164,China)

Routing technology is a key technology of the Ad Hoc network, and it is also one of the most important factors that affect the performance of the network as a whole. As the routing protocols in the traditional fixed networks no longer adapt to the dynamic changes in the topology of Ad Hoc Networks, new Ad Hoc routing protocols must be redesigned. Starting from the basic concept of the Ad Hoc network, an ad hoc network communication effective key agreement protocol based on bilinear pairings and hierarchical routing protocols is proposed. It supports the establishment and dynamic update of initial group secret key and has less traffic that corresponds to the logical key agreement model and actual network topology. The experiment and performance analysis show that the proposed protocol is very effective in the situation of large range, strong ability of equipment processing and poor network communication environment.

Ad hoc Networks; Key Agreement; Hierarchical Routing; Bilinear Pairings

TP311

A

2014.12.17）

1007-757X(2015)03-0008-04

國家自然科學基金項目（61202474）

楊 誠（1975-），男，常州信息技術學院，副教授，碩士，研究方向：計算機網絡技術、移動通信技術，常州，212013

詹永照（1962-），男，常州信息技術學院，教授，博士生導師，研究方向：人機交互、分布式計算，常州，212013