基于Van Der Pauw原理的溶液電導率計

余 翔，張 冰，林 楨，張 瀟，魏佳莉，王曉萍

（1.浙江大學 現代光學國家重點實驗室，光電信息工程學系，浙江 杭州310027；2.浙江省計量科學研究院，浙江 杭州310013）

水既是人類生活生產的重要元素，也是微電子、生物醫藥、食品衛生等行業的關鍵原料，在這些生產應用中，對水質電導率的要求越來越高［1～3］，因此溶液電導率的檢測方法和手段也一直備受關注.

最常用的電導率測量儀器為電極法電導率計，常采用的兩電極結構，電極既是激勵電極又是響應電極，存在著比較嚴重的極化現象而影響測量精度，同時該方法為相對測量法.此后出現的四電極電導率計，采用激勵電極和響應電極分離的測量模式，在一定程度上消除了電極極化對測量結果的影響［4］，但是仍屬于相對測量法.對于相對測量法的電導率計，在使用過程中需要定期用電導率標準溶液對電導池常數進行標定，從而來保證測量精度.由于缺乏低值電導率標準溶液，導致這些相對法無法應用于低值電導率的測量.一些研究機構常采用JONES型電導池測量法，1991年美國國家標準技術局（national institute of standards and technology，NIST）提出了中間可拆卸的新型JONES電導池［5］，此后的二十幾年，不斷有研究人員對該設計進行優化改進［6，7］，由于測量結果準確，已被包括我國在內的許多國家計量研究院作為電導率測定的國標方法；但是該方法對電導池加工精度要求高、測量過程中需要拆裝電導池組件，玻璃結構易碎，難以在實際測量中推廣應用.

本文將Van Der Pauw 原理應用于溶液電導率的測量，由于電導池常數κ僅與電極長度有關，因而無需進行校準，實現了電導率的絕對測量，并分析了對稱性、封閉性等因素對測量結果的影響，最后，通過開展一系列溶液電導率的測量實驗及實際水樣測試實驗，證明了該方法的實用性.

1 測量原理及系統設計

1.1 Van Der Pauw原理

1958年，Van Der Pauw［8］在研究半導體材料時，提出了可以通過四電極結構，測量任意形狀，但厚度均勻材料的電阻率和霍爾系數，測量結構如圖1所示.

在實際測量時，在A、B 兩點施加激勵電流，在C、D 兩點測量響應電壓，并定義RAB，CD為響應電壓與激勵電流之比，同理可得RBC，DA.根據參考文獻［8］有

式中：d 為待測材料的厚度，ρ 表示該樣品的電阻率，由式（1）可得

圖1 Van Der Pauw測量材料電阻率示意圖Fig.1 Original schematic of Van Der Pauw theory

式中：f 為 僅 取 決 于RAB，CD／RBC，DA的 函 數.由 該 式可以看到，樣品的電阻率ρ由RAB，CD、RBC，DA以及材料厚度d 確定.

1996 年 波 蘭 科 學 家Moron 等［9］將Van Der Pauw 原理引入溶液電導率的測量，但是測量時需要一個封閉式的電導池，且電導池高度與電極長度相同，如圖2所示.在測量時，將待測溶液置于圓柱形電導池中，形成高度為h 的溶液柱.4根金屬電極與溶液柱的中軸平行，均勻分布在電導池周邊.在相鄰2根電極1，4上施加激勵電流I1，4，測量電極2，3上的響應電壓U2，3，將U2，3與I1，4的比值定義為溶液電阻R14，23，即R14，23＝U2，3／I1，4；同 理 可 得R12，34＝U3，4／I1，2.

圖2 Van Der Pauw結構測量水溶液電導率原理圖Fig.2 Schematic of Van Der Pauw theory for electrolytic conductivity measurement of solution

電導率σ是電阻率ρ 的倒數，即σ＝1／ρ.因此式（1）改寫為式（3）；電導率公式為式（4）.

式中：f 是R14，23／R12，34的 函 數，根 據 參 考 文 獻［8］，f 可表示為

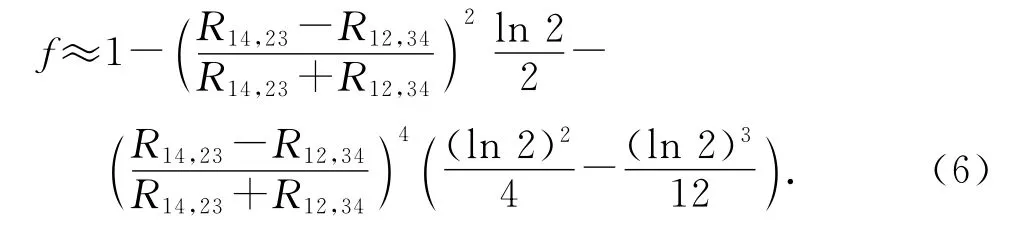
當R14，23、R12，34近似相等時，則f＝1，此時＝R14，23＝R12，34.根據式（4）可得溶液的電導率為

式中：κ＝ln 2／πh為電導池常數，僅取決于電極長度h；G 為溶液電導，是溶液當量電阻的倒數.在實際測量時，在激勵電極上施加激勵電流，測量響應電極間的電壓，計算得到，再根據電極的電導池常數κ，就可得到被測溶液的電導率.

這種四電極結構能夠有效降低兩電極結構中由于電極極化效應引起的測量誤差.其電導池常數κ僅與電極高度有關，而不需要使用電導率標準溶液對κ進行標定，因此Van Der Pauw 法是一種電導率的絕對測量法，設計不同的電極長度h，就可以獲得不同的電導池常數.

1.2 Van Der Pauw電導率測量系統

1.2.1 交流電壓激勵源 按照Van Der Pauw 原理在激勵電極上施加交流電流，從電學原理上分析，電流激勵和電壓激勵瞬間產生的電場是一致的，綜合激勵源設計的難易度，本研究選擇交流電壓源作為電極激勵信號［10］.通過實時采集串聯在激勵電極回路中精密電阻R 兩端的電壓，獲得實時的激勵電流，具體設計如圖3所示.

圖3 電壓激勵與測量電路的連接Fig.3 Circuit diagram of excitation source

電壓激勵信號US通過R 連接到激勵電極1、4兩端，電阻R 兩端的電壓為UR，因此激勵電流為I＝UR／R，從電極2、3獲取溶液的響應電壓Uout；此時溶液的當量電阻＝Uout／I＝UoutR／UR，將代入式（7）可得溶液電導率計算公式如（8）所示.因此通過測量Uout、UR，結合電極的電導池常數和精密電阻R 的阻值，即可得到溶液的電導率值.

1.2.2 信號采集與運算 交流電壓激勵信號由DDS芯片AD9833產生，激勵信號選用頻率為250 Hz，幅值為0.6V 的正弦波.取樣電阻兩端電壓UR和響應電壓Uout，分別經差動放大、有效值電路后，由模數轉換器進行采集，再通過計算得到溶液的實時電導率值.

由于水溶液的電導率受溫度的影響較大，為了滿足實際測量需求，設計中增加了以Pt1000溫度傳感器為核心的溫度測量模塊.根據不同測量需求，可以選擇對電導率值進行溫度補償，其計算公式如式（9）：

式中：a為溫度系數；σt、σR分別為在溫度t 和tR時的電導率值，tR通常選擇為25 ℃.

2 電極設計與電導池常數

2.1 對稱四電極結構

由公式（7）可知，電極尺寸確定后，溶液電導率由其當量電阻確定，因此測量的準確性決定了電導率的測量精度.由Van Der Pauw 原理可知，式（7）成立的條件是＝R14，23＝R12，34，需要4個電極嚴格對稱且長度完全一致.為保證電極的對稱性，設計了徑軸二維可調的四電極結構，如圖4所示.

圖4 徑軸二維可調四電極示意圖Fig.4 Four-electrode with axial-radial two-dimensional adjustment structure

圖中①和②為長度微調旋鈕和徑向位置微調旋鈕，能夠實現徑軸2個維度0.01～8mm 的距離調整.經計算可 知，由于電極對稱性導 致R14，23、R12，34存在±1%誤差時，修正函數f 的高階誤差小于0.001%［11］，此時認為該誤差可以忽略.

電極材料選擇較高導電性和耐腐蝕性的不銹鋼材料（電阻率為0.70×10-6Ω·m），為保證電極的剛度，選擇直徑為2 mm，以保證合適的長徑比.調整電極時，外部激勵信號分別加載在電極1，4兩端和1，2兩端（圖2），分別測量電極2，3兩端和3，4兩端的響應電壓，通過微調電極長度和徑向位置使響應電壓與激勵電流的比值，即對稱當量電阻R12，34，R23，14盡可能相等，最終調整到兩者 的相對 誤差在0.5%以內.

2.2 封閉式電導池

電導池是電導率計的重要組成部分，根據Van Der Pauw 測量原理，該方法需要配合封閉式的電導池［9］.電導池腔設計為圓柱形，選擇介電系數小，抗酸堿和多種有機溶劑的聚四氟乙烯材料.為證明電導池封閉性對測量結果的影響，本文設計了3款不同封閉程度的電導池開展實驗研究，如圖5 所示.圖（a）為封閉性電導池，其電極緊貼電導池內壁與池底；圖（b）為半封閉電導池，其電極緊貼內壁，池底開放；（c）為開放式電導池，電極遠離內壁，且池底開放.實驗時將（b）和（c）分別置于一個底部均勻且形狀相同的大燒杯中.

圖5 3款不同封閉性的電導池Fig.5 Three different conductivity cells

根據國標GB／T 27503-2011《電導率儀的試驗溶液—氯化鈉溶液制備方法》［12］配制一系列不同電導率濃度的NaCl溶液，選擇長度h＝22mm 的電極（電導池常數κ＝0.1cm-1）.分別用這3種電導池對電導率為0～250μS／cm 范圍內的多種電導率溶液進行測量，得到測量結果記為σVDP；同時用梅特勒高精度Inlab Trace電導率儀的測量值作為實際值（記作σM）進行比對，測量結果如圖6所示.3種電導池的測量值σVDP與實際值σM進行線性擬合，擬合曲線分別為

由上述擬合公式可見，封閉式電導池的測量值與實際值有很好的一致性，如式（10）.而半封閉和開放式結構電導池的測量結果，與實際值需要進行換算，而具體換算關系需要用標準溶液進行標定獲得.因此Van Der Pauw 四電極結合封閉式電導池，構建了電導率的絕對測量方法.

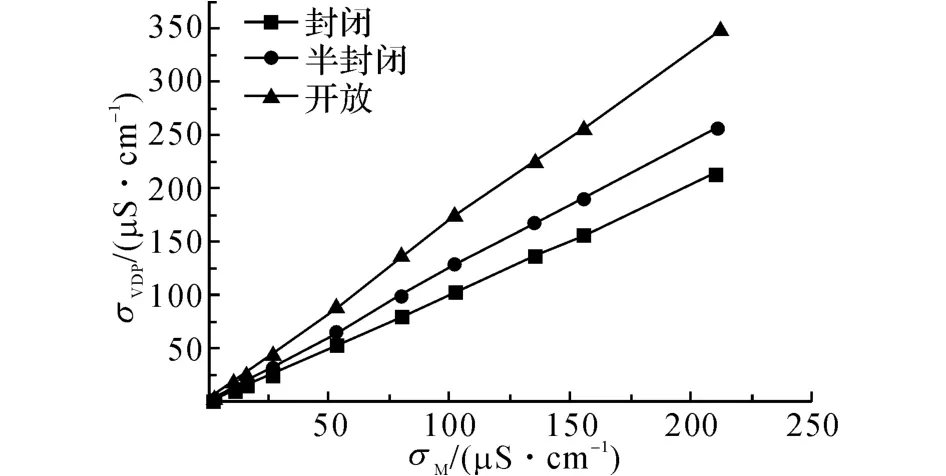
圖6 不同封閉程度的Van Der Pauw電導池測量結果Fig.6 Measurement results of 3different conductivity cells

2.3 電導池常數

如何正確選擇電導池常數在很大程度上會影響溶液電導率的測定精度.根據美國材料與試驗協會提供的溶液電導率計電導池常數的推薦表，設計了3款電極長度分別為44、22 和5.5 mm 的四電極，對應的電導池常數分別為0.05、0.1和0.4cm-1.根據3.2節電導率溶液的配制方法，配制了電導率值范圍在0～2 500μS／cm 的標準溶液進行實驗測試，分別用3款電極測量得到溶液的電導率，同時以Inlab Trace電導率儀的測量結果為真實值.測量結果和擬合曲線如圖7所示.

圖7 不同電導池常數測量結果對比（log坐標）Fig.7 Measurement results of 3different cell constants

分別對3款電極的測量結果，在0～2 500μS／cm 范圍內、以及分段進行擬合，可以得到3種不同電導池常數電極的最佳測量范圍，具體范圍及擬合公式如式（13）、（14）、（15）所示：

電導池常數κ＝0.05cm-1，最佳測量范圍：

電導池常數κ＝0.1cm-1，最佳測量范圍：

電導池常數κ＝0.4cm-1，最佳測量范圍：

經過分析可知，在0～2 500μS／cm 整個范圍內，3款電極的實際測量曲線均呈線性，均可實現正確測量.但當要求高精度測量時，可以根據實際水樣的電導率范圍，選擇合適的電導池常數κ，以提高測量的準確性.

3 實際水樣測試實驗與結果

為驗證Van Der Pauw 法電導率計測量實際水樣時的準確性和適用性，運用κ＝0.1cm-1的電極進行幾種實際水樣的測量（結果記為σVDP），同時使用Inlab Trace電導率儀（結果記為σM）進行對比測量，η為相對偏差兩者在同一溫度下的測量結果如表1所示.由結果可見，在0～500μS／cm 內實際水樣，除小于10μS／cm 去離子水的測量誤差偏大外，其他水樣的測量相對誤差均小于1.0%，若都將結果溫度補償到25℃時測量精度不變.表明該電導率計，能夠滿足實際生活中大多數水體的測量需求.

表1 實際水樣的測試結果Tab.1 Measurement results of some water samples

4 結 語

基于Van Der Pauw 原理的電導率計，可以實現溶液電導率的絕對測量.采用激勵電極和響應電極分離的對稱四電極結構，能夠有效地避免兩電極結構的電極極化和電容效應，滿足高精度的測量需求.其電導池常數僅由電極長度確定使得電導率計設計變得簡單，采用交流電壓源作為激勵信號簡化了電路設計.經過配制的標準電導率溶液和實際水樣的檢測實驗，表明這種電導率的絕對測量方法具有較高的精度和良好的線性范圍，因此具有很好的應用前景和推廣價值.

（

）：

［1］BHATIA R，DILLEEN J W，ATKINSON A L，et al.Combined physico-chemical and biological sensing in environmental monitoring［J］.Biosensors and Bioelectronics，2003，18（5）：667-674.

［2］MCCLESKEY R B，NORDSTROM D K，RYAN J N，et al.A new method of calculating electrical conductivity with applications to natural waters［J］.Geochimica et Cosmochimica Acta，2012，77：369-382.

［3］GRYSINSKI T，MORON Z.Planar sensors for local conductivity measurements in biological objects—Design，modelling，sensitivity maps［J］.Sensors and Actuators B-Chemical，2011，158（1）：190-198.

［4］周明軍，尤佳，秦浩.電導率傳感器發展概況［J］.傳感器與微系統，2010.29（4）：9-11.ZHOU Ming-jun，YOU Jia，QIN Hao，et al.Overview on the development of conductivity sensor［J］，Transducer and Microsystem Technologies，2010，29（4）：9-11.

［5］WU Y C，KOCH W F，PRATT K W.Proposed new electrolytic conductivity primary standards for kcl solutions［J］.Journal of Research of the National Institute of Standards and Technology，1991，96：191-201.

［6］BRINKMANN F，DAM N E，DEAK E，DURBIANO F，et al.Primary methods for the measurement of electrolytic conductivity［J］.Accreditation and Quality Assurance，2003，8（7／8）：346-353.

［7］ORRU E，DURBIANO F，ORTOLANO M.Reference measurement system for low electrolytic conductivity values with a flowing solution［J］.Measurement Science and Technology，2013，24 0359033.

［8］VAN DER PAUW L J.A method of measuring specic resistivity and Hall effect of discs of arbitrary shape［J］.Philips Research Reports，1958，13：1-9.

［9］MORON Z，RUCKI Z，SZCZEPANIK Z.The possibility of employing a calculable four-electrode conductance cell to substitute for the secondary standards of electrolytic conductivity［J］.IEEE Transactions on Instrumentation and Measurement，1997，46（6）：1268-1273.

［10］魏佳莉.基于Van Der Pauw 法的水溶液電導率絕對測量系統研究［D］.杭州，浙江大學，2013.WEI Jia-li.The research of measuring system of electrical conductivity of aqueous solution based on Van Der Pauw theory［D］.Hangzhou：Zhejiang University，2013.

［11］RIETVELD G，KOIJMANS C V，HENDERSON L C A，et al.DC conductivity measurements in the Van Der Pauw geometry［J］.IEEE Instrumentation and Measurement Society，2003，52（2）：449-453.

［12］GB／T 27503-2011.電導率儀的試驗溶液—氯化鈉溶液制備方法.［S］.北京：國家機械工業局，1999.GB／T 27503-2011.Test solutions of electrolytic condcutivity analyzer—Preparation method of sodium chloride solutions.［S］.Beijing：State Bureau of Machine-Building Industry，1999.