基于改進魚群尋優算法的天線陣方向圖綜合

黃 勇，玄曉波，姚鳳薇，曹 揚

（上海無線電設備研究所 上海 200090）

在雷達和通訊等領域中，經常需要對陣列天線方向圖進行特殊賦形設計。根據賦形條件求解出陣列的單元數目、空間排布、幅度相位分布等參數的過程，即為綜合。陣列綜合是一個復雜的多維非線性優化問題。當目標方向圖比較復雜或者存在較多約束條件時，切比雪夫、泰勒等經典的解析方法就難以進行有效求解[1-2]，需要突破常規發展一種新的實現方法。

智能優化算法在解決全局性多目標優化問題時具有良好的適用性。近年來，在智能算法領域出現了一系列新穎算法，并作為解決傳統復雜問題的一種新興演化計算技術迅速成為了國內外的研究熱點。目前，遺傳算法[3-4]、差分進化算法[5]和粒子群優化算法[6]等智能算法已被應用到了天線領域，尤其是在陣列天線的優化設計方面。常規的智能優化算法雖然在深零陷生成和低旁瓣抑制上取得了良好的效果，但對于有著多零點和低旁瓣等多約束條件的陣列天線進行綜合時仍難以避免早熟，易陷入局部收斂。

誕生于2002年的魚群算法一種新穎的群體智能算法[7-8]，通過虛擬實現生物的視覺感官功能，模擬魚類的覓食、群聚、追尾、隨機等生物行為在搜索域中進行尋優，很適合解決天線陣列綜合等復雜的多維非線性優化問題。針對傳統算法容易陷入局部收斂的不足，本文提出了一種改進的魚群尋優算法，將混沌優化算法和人工魚群算法進行了結合，并將人工魚的視野范圍和步進設置成了動態調整，首次成功地將其應用于陣列天線方向圖綜合中，通過仿真驗證了新算法的有效性。

1 改進的魚群尋優算法簡介

1.1 原始魚群算法

人工魚群算法通過模擬魚群的覓食、聚群、追尾、隨機等行為，且這些行為隨機進行著互相轉換，利用魚群間的相互協作來找尋出問題最優解[7]。以求解極大值為例，假定魚所在位置的食物濃度為f（X），魚群算法的簡要流程如圖1所示。

1.2 改進的魚群尋優算法

1.2.1 復合混沌映射

初始魚群的個體分布狀況直接影響著智能算法的計算準確性和全局收斂性。若初始魚群分布性差，將導致算法收斂速度緩慢，甚至不收斂。在無法預知最優解存在區域的情況下，初始魚群應盡可能地分散分布。混沌是一種普遍存在的非線性現象，混沌搜索具有內在隨機性、初值敏感性、遍歷性等特點。為確保初始魚群的多樣性，利用混沌序列來彌補智能算法初始值較隨機的不足，借鑒文獻[9]的思想，魚群的初始化分別采用Logistic序列和Tent序列，其表達式分別如下式（1）、（2）所示：

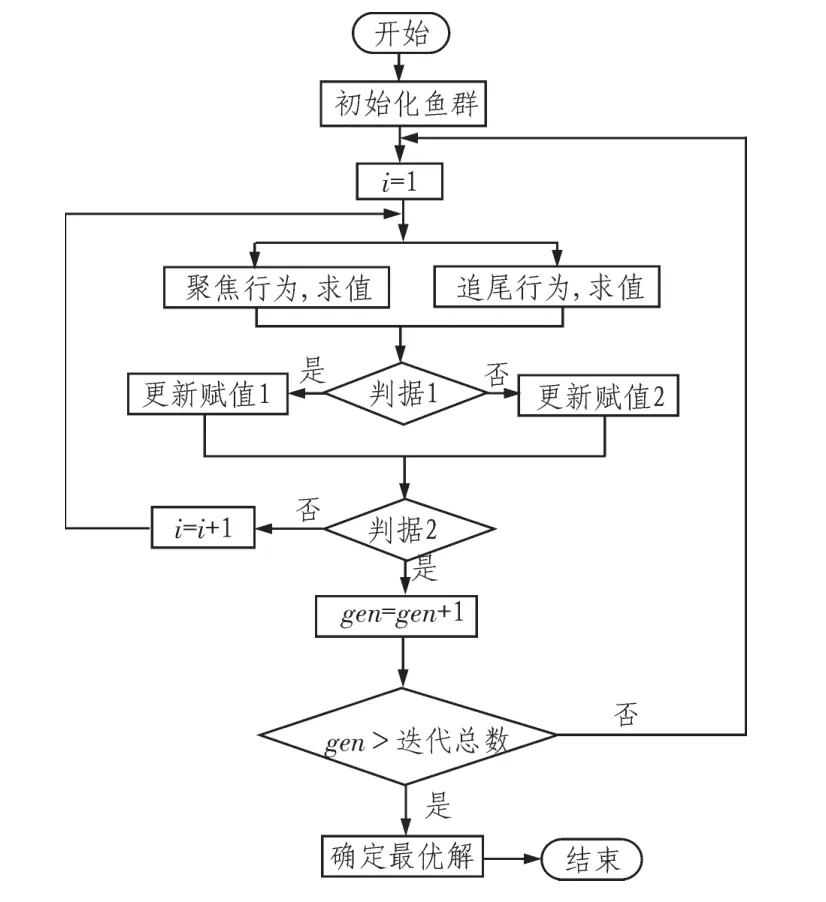
圖1 人工魚群算法流程圖Fig.1 Flowchart of artificial fish swarm algorithm

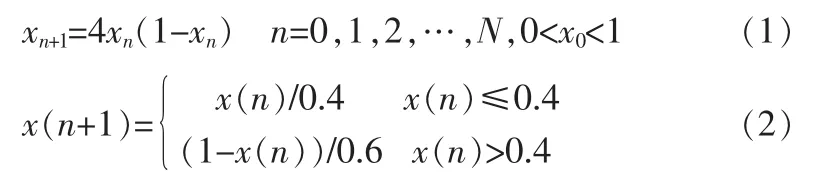
1.2.2 視野的動態調整

由群體智能算法的空間搜索機制可知，群體智能算法在計算早期應該著重于全局搜索，以保證較快的收斂速度和更廣的搜索范圍；在計算后期則應該著重于精細的局部搜索，實行局部搜索，以提高算法的求解精度。為符合Logistic模型的變化規律，借鑒粒子群算法中將慣性權重設置成動態變化的方法[9]，將魚群算法中的視野范圍也設置成動態變化的，其表達式如式（3）所示。

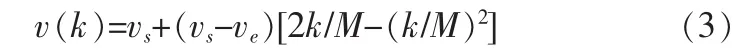
式中，k為迭代次數；vs為初始視野范圍；ve為迭代至最大次數時的視野范圍；M為最大迭代次數。隨著迭代不斷進行，視野范圍v最近收斂于ve。

1.2.3 步進的動態調整

個體魚移動步進越大，個體向最優位置靠近的速度越快，若在算法的早期采用較大的步進，收斂速度就越快，跳出局部最優的能力也就越強；反之，如果在算法的早期采用較小的步進，搜索范圍小，收斂速度慢，且易陷入局部最優。同理，在算法的后期，在最優解搜索大致范圍已確定的條件下，若采用較小的步進，可以提高算法的求解精度。動態步進的表達式為

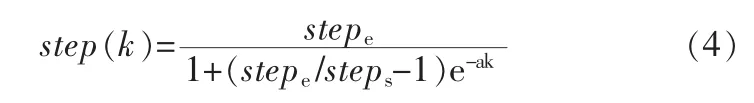
式中，k為迭代次數；steps為初始步進；stepe為迭代至最大次數時的步進；a為衰減率。

2 陣列方向圖綜合

對于由N個理想點源組成的直線陣，以陣列的第一個單元為空間位置參考點，在不考慮單元之間耦合的條件下，天線陣列的遠場方向圖可表示為

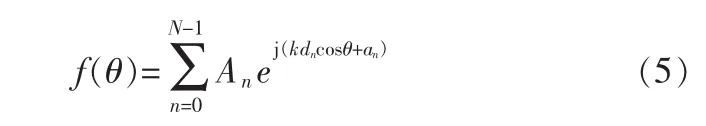
式中，θ為空間輻射角，k為波數，dn為從第n個單元到第一個單元的距離（波長的倍數），An和an分別表示第n個單元的幅度和相位。

利用切比雪夫、泰勒等經典方法來實現超低副瓣綜合存在著各種限制，需要突破常規發展一種新的方法。魚群算法是通過虛擬實現生物的視覺感官功能，在搜索域中進行動態尋優，具有對初值不敏感、全局漸進收斂等優點，很適合用以天線方向圖綜合等復雜的多維非線性優化問題。用改進魚群算法綜合方向圖的目的就是根據波束形狀來求解陣列天線的激勵幅度、相位和單元間距。適應度函數的設計是算法的關鍵，它的好壞直接決定了優化效果，它必須根據具體問題進行具體設計。對應線性陣列的綜合，適應度函數采用文獻中論述過的適應度函數[7]：

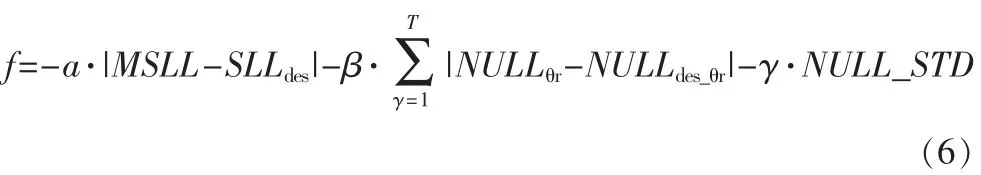
式中，MSLL和SLLdes為計算最大相對旁瓣電平和目標旁瓣電平；NULLθr是計算目標位置 θγ的零陷，NULLdes_θr是相應位置零陷深度值；NULL－STD表示多個零陷的方差，這是為了克服僅使用最高零陷深度作為優化項而導致的零陷不均衡現象；α、β和γ是各項指標的權值，T是需控制零陷深度的零陷總數。

采用20個天線單元組成的均勻直線陣來驗證魚群算法是否適合超低副瓣綜合。所有單元相位相同，單元間距為0.6γ，副瓣低于－40 dB，所有的零陷深度不低于－70 dB，主瓣波束寬度不大于18°。綜合所得的方向圖和電流分布分別如圖2和圖3所示，魚群算法尋優所得的最優方向圖的各項指標參數均優于目標值。對魚群算法和切比雪夫兩種方法的綜合效果進行了對比，相對于近似的電流分布，在波束寬度等大的條件下，通過魚群算法綜合所得的方向圖副瓣更低。

魚群算法除了可以實現超低副瓣方面外，還可以在副瓣、副瓣間差異、波束寬度、零陷等指標需要滿足一定約束條件時對一特定角度范圍內的副瓣進行抑制。若優化條件為所有單元相位相同，單元間距為0.6λ，副瓣低于－35 dB，主瓣波束寬度不大于 18°，30°～40°波束范圍內的副瓣低于－70 dB，綜合所得的方向圖如圖4所示。從圖4可以看出，線陣方向圖的副瓣和特定區域的零陷均達到了優化指標要求。

除了能實現常規的方向圖外，魚群算法還能實現特殊波束的賦形設計，如圖5所示的余割波束賦形。進行此類賦形設計時，適應度函數一般選取賦形區、旁瓣區的目標函數和綜合所得方向圖兩者間偏差的均方差來進行賦形設計。

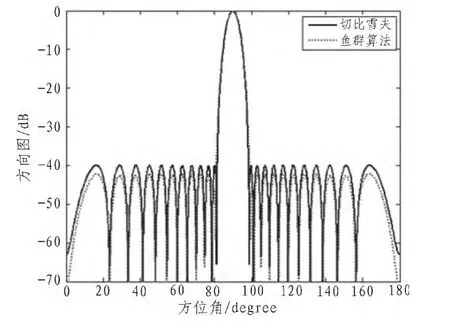
圖2 20陣元均勻線陣歸一化方向圖Fig.2 Normalized power pattern for 20 elements with the same interelement spacing

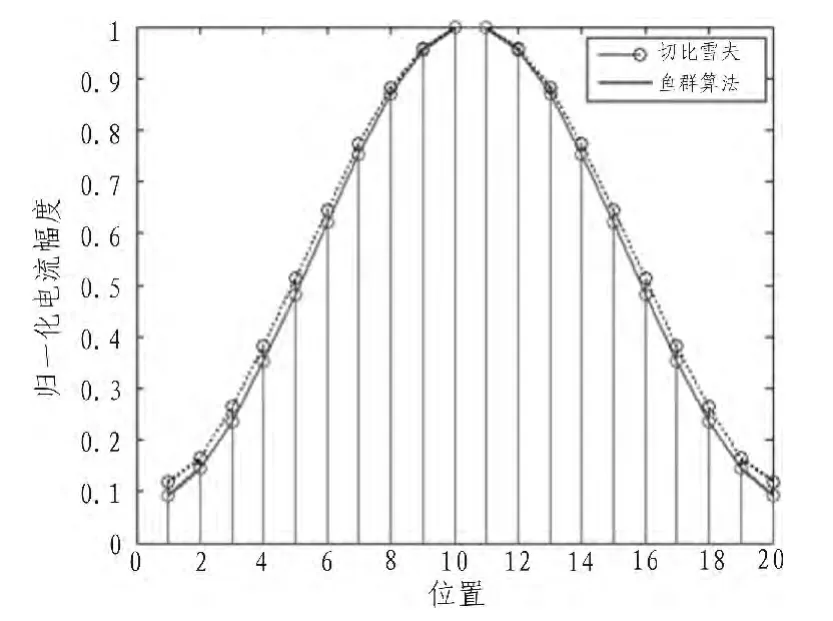
圖3 陣列歸一化電流分布圖示Fig.3 Normalized current value of the array

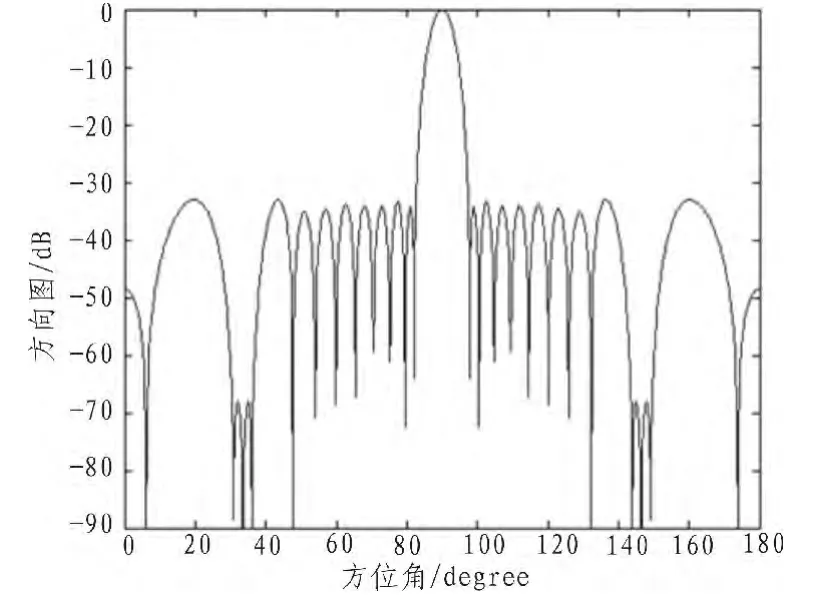
圖4 30°～40°范圍內具有低副瓣的方向圖Fig.4 The pattern with low side-lobe between 30°to 40°

綜上，通用魚群尋優算法來實現超低副瓣抑制、零陷控制和特殊波束賦形設計是可行的，且比傳統方法效果更優，運算的時效較傳統算法有大幅度提升。

3 結束語

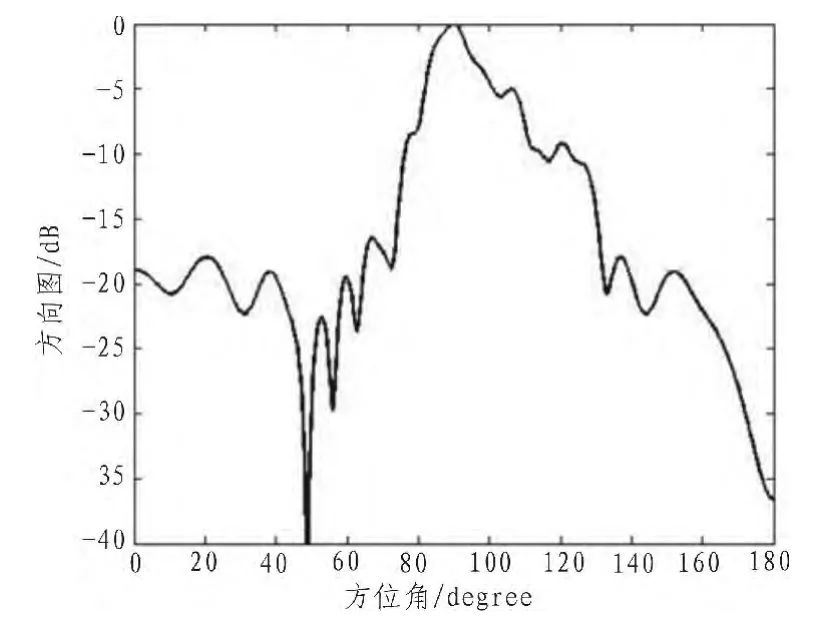
圖5 余割平方波束賦形Fig.5 The pattern of Csc beam

針對傳統智能算法在實現陣列方向圖綜合中存在早熟收斂，易陷入局部極值的缺陷，本文介紹了一種可以進行低副瓣抑制和波束賦形的新方法，即改進的魚群算法。該算法將混沌算法和魚群算法相結合，采用混沌序列初始化魚群，以提高種群的多樣性和搜索的遍歷性，有效地避免了早熟收斂。為了在將算法早期的全局搜索和算法后期的精細局部搜索有機結合起來，借鑒粒子群算法中的動態慣性權重方法，將人工魚的移動步進和視野范圍均設置成動態變化的，以滿足Logistic模型的變化規律。

為了驗證算法的實用性和有效性，利用其進行陣列天線方向圖綜合和波束賦形設計。工程實例表明，該算法在解決多參數、非線性的復雜問題時具有良好的適用性。

[1]Robert C Hansen，Deng P.No-uniformly spaced super directive antenna arrays patel[J].IEEE， Antenna Array，2002，38（12）:131-135.

[2]Warnick，Jensen.Antennas and propagation for wireless communications[J].IEEE Transition on Antennas and Propagation，2001，49（13）:32-39.

[3]王宏建，高本慶，劉瑞祥.基于遺傳算法的單脈沖陣列天線優化[J].中國科學工程，2002，4（5）:84-87.

[4]范瑜，金榮洪.基于一種新的遺傳算法的天線方向圖綜合技術[J].電波科學學報，2004，19（2）:182-186.

[5]謝歡歡，楊伯朝.基于差分進化算法的陣列天線波束賦形研究[J].現代導航，2012，6（3）:219-224.

[6]齊美清，汪偉，金謀平.基于粒子群算法的天線陣方向圖優化[J].現雷達科學與技術，2008，6（3）:231-234.

[7]王培崇，雷鳳均，錢旭.改進人工魚群算法及其收斂性分析[J].科學技術與工程，2013，13（3）:616-620.

[8]李曉磊，錢積新.基于分解協調的人工魚群優化算法研究[J].電路與系統工程，2003，8（1）:1-6.

[9]劉建霞，李楠，謝克明.改進的思維進化算法在陣列天線綜合中的應用[J].測試技術學報，2009，23（4）:331-336.