GPS在高精度工程測量控制網中的應用研究

何光源

（鄭州中核巖土工程有限公司，河南 鄭州 450000）

1 前言

現階段，一般通過布設三角網，利用高精度全站儀進行邊角聯測建立高精度測量控制網。 這種方法的內外業工作量較大，各方面要求較高。 同時，由于受到現場地形、通視等情況的影響，控制網的圖形條件不容易滿足，點位精度不均勻，整體精度不容易控制，測量工作勞動強度和難度相對較大。

GPS 全球定位系統， 是隨著現代科學技術的迅速發展而出現的新一代精密衛星定位技術。 近年來GPS 接收機質量和精度不斷提高， 用GPS 測量坐標的絕對和相對精度提高到厘米級甚至亞毫米級， 大大拓展了它的應用范圍和在工程測量中的作用。 多年來在控制測量中應用GPS 的經驗表明， 利用GPS 建立高精度工程測量平面控制網是可行的， 但GPS 建立的高程控制網在現階段達不到工程施工的要求。 對于GPS 建立高精度工程測量平面控制網能達到怎樣的精度， 如何進行內外業工作使GPS建立的平面控制網符合施工測量要求這些問題， 本項目在工程實踐的GPS 測量數據中增加多個已知條件進行平差處理， 并將獲得的結果和高精度全站儀測量結果進行比較來加以說明， 并進一步研究如何使GPS 在高精度工程測量平面控制網的測量中獲得較高精度。

2 GPS 測量的基本原理

GPS 測量的基本原理就是將兩臺或兩臺以上的GPS接收機分別安置在測量基線的兩端，同步觀測相同的GPS衛星[1]。 以GPS 衛星和用戶接收機天線之間距離（或距離差）的觀測量為基礎，確定基線端點在協議地球坐標系中的相對位置或基線向量。 通過GPS 平差軟件對所獲得的基線進行解算， 在WGS84 坐標系統下進行三維自由網平差，并利用已有控制點進行平差處理，獲得控制點的坐標成果。 GPS 定位方法主要有偽距法和載波相位測量法。

3 GPS 測量的特點

GPS 測量主要有以下特點：

3.1 在大地控制測量中精度高。 GPS 控制測量的精度在大地控制測量中高于常規利用全站儀進行的三角測量。

3.2 測站之間不需通視。 GPS 測量可根據現場情況和測量的實際需要確定點位， 選點和測量工作更加靈活方便。

3.3 儀器操作簡單、觀測方便。 測量人員只需對中、整平、量取GPS 天線高及開機后設定參數，GPS 接收機即可進行自動觀測和記錄，操作已達智能化。

3.4 可進行全天候作業。GPS 接收的衛星數目較多，且分布均勻，可在任何時間進行觀測。

3.5 在工程測量中應用廣泛。GPS 可用于精密工程，如控制網測量、變形監測、隧道貫通測量，也可用于測繪各種比例尺地形圖和施工放樣。

3.6 GPS 測量的勞動強度優于其他測量方法。

4 工程實例

某電廠因工程施工需要建立高精度工程測量控制網，要求在現場布設12 個控制點，控制網的平面點位精度要求在2mm 以內。 其主要目的和作用是：為廠區內各級控制網的建立、 廠區形變監測提供基準， 為廠區內建（構）筑物施工定位、放樣測量、設備安裝測試及局部控制網加密提供依據。

控制網測量在施工初期通視性較好， 隨著施工的進行， 控制點的通視性越來越差， 全站儀的測量也更加困難。 為了找到更加可行的測量方法，在本工程項目中利用全站儀進行三角測量的同時， 利用GPS 對部分控制點進行測量，對兩種測量方法獲得的成果進行比較，研究應用GPS 建立高精度工程測量控制網的可行性， 并為日后利用GPS 進行測量提供實踐依據。

4.1 控制網觀測方案的設計

控制網的觀測方案按照規范要求[2]，依據現場具體情況和三角測量、GPS 測量的特點與具體要求進行設計。

4.1.1 三角測量方案

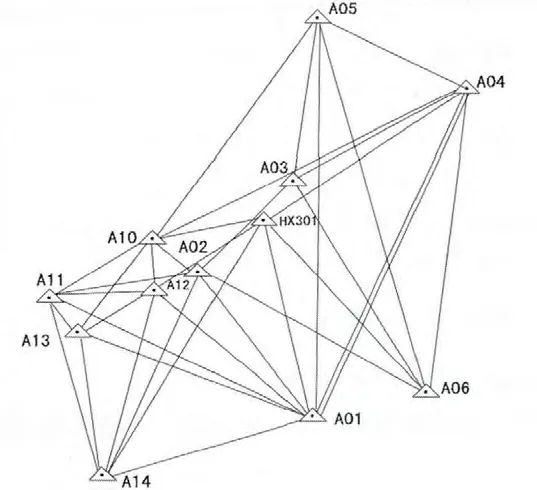
圖1

三角測量利用TC2003 全站儀進行測量，水平角采用全圓觀測法觀測6 個測回， 垂直角采用對向觀測中絲法觀測3 個測回。 邊長采用正倒鏡往返觀測3 測回測量斜邊，最終結果取平均值。 同時，在測量邊長時測線的兩端測量溫度和氣壓，在內業中進行邊長氣象改正。 控制網圖如圖1。

4.1.2 GPS 測量方案

為了使GPS 測量獲得精度較高的數據，在12 個控制點中選擇8 個測站進行測量，要求上空盡可能開闊，在15高度角以上沒有成片的障礙物,周圍約200m 的范圍內沒有強電磁波干擾源,并且測站要遠離對電磁波信號反射強烈的地點[3]。

GPS 測量采用四臺Leica 雙頻GPS 接收機進行，測量時GPS 接收機安置在觀測墩強制歸心基座上。 設置衛星截止高度角大于15，有效衛星總數不少于6 個，重復觀測時段數不少于2 個時段，歷元采樣時間間隔為15s，GDOP值小于6，觀測時段長度大于90min。 采用靜態測量作業模式進行測量， 當GDOP 值大于6 時， 適當延長觀測時間。 GPS 測量時確保一定的重復設站次數，并對異步環中相鄰很近的兩個點進行同步觀測， 以提高整個網的相對精度。 控制網圖如圖2。

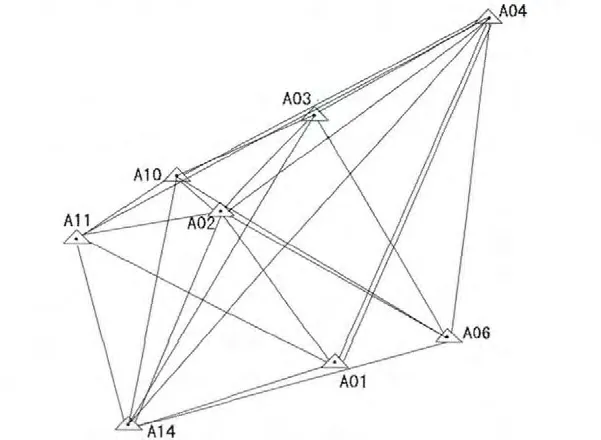
圖2

4.2 數據處理

本次三角網測量， 共組成16 個三角形， 總邊長13260.1410m,平均邊長378.8610m，最小邊長88.3790m，最大邊長835.313m， 三角形最大內角閉合差為3.45″，最小為0.01″。

三角測量數據經外業數據計算各項限差符合規范要求后, 使用南方公司的南方平差易2005 平差軟件以A01為起算點，以A01-A04 為起算方向進行平差處理。平差前方向中誤差0.54″，經平差后，最大點位誤差[A14]=1.4mm，最小點位誤差[A12]=1.0mm，平均點位誤差=1.2mm，最大點間誤差=2.7mm，最大邊長比例誤差1/161685，平面網驗后單位權中誤差=0.70s。 平差結果表明，三角測量方法在本次測量中取得較高的精度。

GPS 測量數據處理先利用天寶GPS 測量平差軟件進行基線解算，解算出的基線比率和參考變量均符合要求。最后導出基線解算成果，利用CosaGPS 平差軟件，增加已知邊長與方位角的多種方法進行平差計算， 平差結果如下：

4.2.1 利用兩個已知坐標進行二維約束平差， 最弱點A14 的點位中誤差為1.7mm， 最弱邊SA02-A10 的邊長比例誤差為1/189000。

4.2.2 利用兩個已知坐標與兩個已知邊長進行二維約束平差， 最弱點A14 的點位中誤差為1.5mm， 最弱邊SA10-A02 的邊長比例誤差為1/177000。

4.2.3 利用兩個已知坐標與三個已知邊長進行二維約束平差， 最弱點A14 的點位中誤差為1.4mm， 最弱邊SA02-A10 的邊長比例誤差為1/184000。

4.2.4 利用兩個已知坐標、 三個已知邊長和一個已知的方位角進行二維約束平差， 最弱點A14 的點位中誤差為1.2mm， 最弱邊SA10-A02 的邊長比例誤差為1/174000。

4.3 成果比較

4.3.1 邊長成果比較[4]

為了檢驗GPS 測量的邊長成果可靠性，利用TC2003全站儀觀測經氣象改正后的邊長， 與GPS 二維約束平差后的邊長進行比較。

通過表1 的多種GPS 平差結果的邊長與TC2003 全站儀測量的邊長的比較可以看出， 隨著GPS 平差已知條件增加，GPS 二維約束平差后的邊長與TC2003 全站儀觀測經氣象改正后的邊長整體上越來越接近， 說明增加GPS 平差中已知條件，可以提高GPS 測量邊長的精度。因而，在進行GPS 測量時，只要統籌考慮觀測時間和測量中影響到GPS 測量精度的因素，選擇質量較好、精度較高的儀器，設計合適的網形，避開不利因素進行測量，充分利用高精度的已知數據參與GPS 二維平差，GPS 測量邊長就可以達到精密工程測量的要求。

4.3.2 坐標成果比較

為了檢查GPS 平差坐標精度的可靠性， 對三角測量平差獲得的坐標與GPS 二維約束平差后獲得的坐標進行比較[5]。

通過表2 多種GPS 二維約束平差后獲得的坐標與三角測量平差獲得的坐標的比較可以看出：GPS 二維約束平差后的坐標與三角測量平差獲得的坐標有差別， 但隨著GPS 平差已知條件的增加，GPS 二維約束平差后獲得的坐標接近三角測量平差獲得的坐標。 因而在GPS 的數據平差處理中，增加高精度的已知數據參與約束平差，可以獲得較高的GPS 測量坐標精度。

表1 全站儀測量的邊長與GPS 二維約束平差的邊長比較

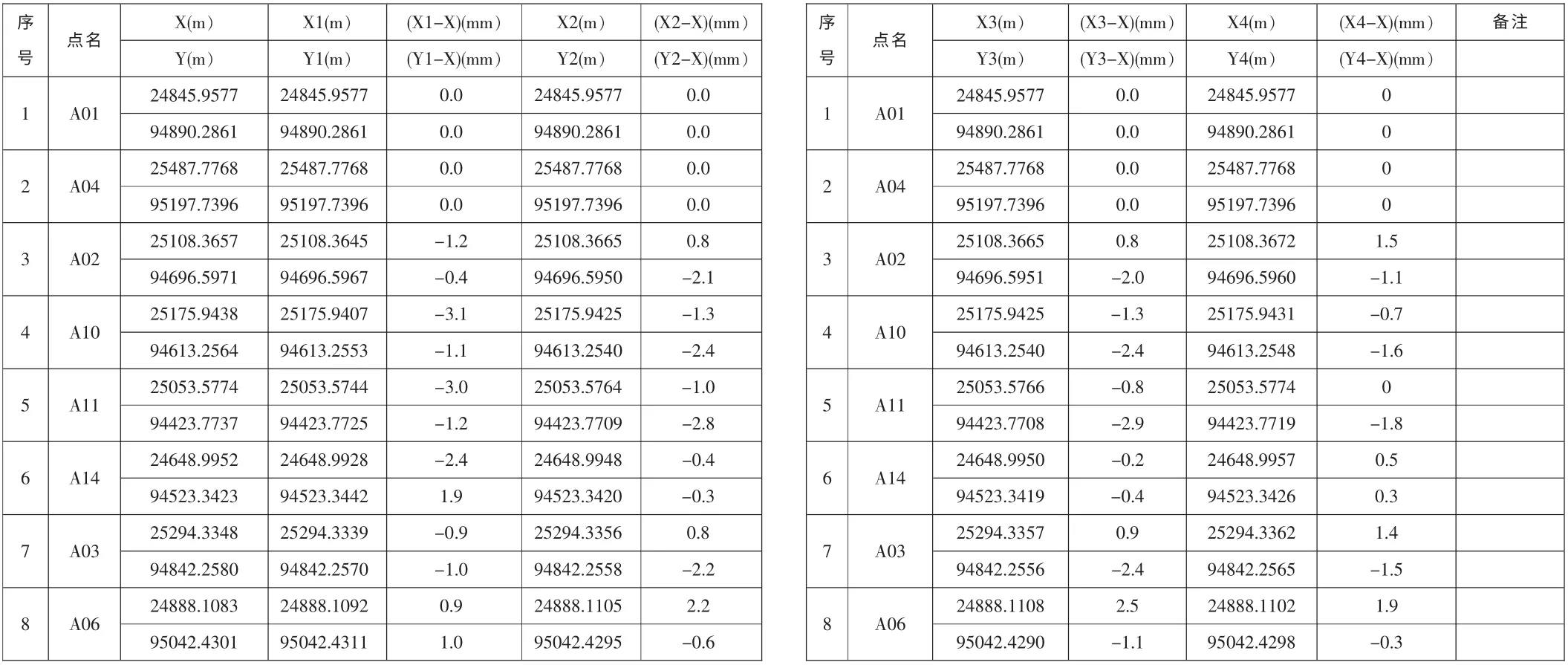
表2 三角測量平差坐標與GPS 二維約束平差的坐標比較

5 結論

分析工程實例中的數據，我們可看出：

5.1 在GPS 測量中參與二維平差的已知數據越多，最弱點的點位中誤差越小。

5.2 隨著已知數據的增加，GPS 測量二維平差數據越接近高精度的三角測量平差數據。

5.3 GPS 測量中只要觀測方法采用得當， 有適當高精度已知數據參與平差，GPS 測量的坐標就可以達到2mm 的點位精度。

由此可見，當觀測現場的通視條件較差，控制網圖形條件達不到要求，利用全站儀測量難以達到精度要求時，利用GPS 進行測量，并在GPS 平差中加入全站儀測量的高精度邊和方位角作為已知數據， 在GPS 的平差軟件中進行二維約束平差，可以提高控制網測量精度。 但需要有適當高精度已知數據才能達到工程施工測量的要求，這就需要配合使用高精度的全站儀。 同時，GPS 測量精度還受到作業的環境、儀器性能和軟件功能的影響，如何降低甚至消除這些影響，GPS 測量如何進行才能獨立地完成高精度工程測量控制網的建立， 還需要較長時間的探索和進一步研究。 隨著科學技術的發展，GPS 測量的精度會越來越高，其將在高精度工程測量中得到廣泛應用。

［1］中華人民共和國國家標準.GB/T 18314-2001.全球定位系統（GPS）測量規范［S］.北京：中國標準出版社，2001.

［2］中華人民共和國國家標準.GB50026-2007.工程測量規范［S］.北京：中國計劃出版社，2007.

［3］王增學. 如何提高GPS 在工程測量應用中的精度［J］.科技創新導報，2009（1）：62-66.

［4］蘇永年.GPS 網與測邊網在施工控制網中的應用研究［J］.四川測繪，2001，24（4）：7-101.

［5］張小望，楊錦.GPS 在大型電廠高精度廠區控制網測量中的應用［J］.電力勘測與設計，2005（2）：43-48.