關于一階非齊次線性微分方程的求解問題

吳小蘭

（福建電力職業技術學院，福建 泉州362000）

關于一階非齊次線性微分方程的求解問題

吳小蘭

（福建電力職業技術學院，福建 泉州362000）

給出并證明了兩個定理，利用這兩個定理求解一階非齊次線性微分方程。

非齊次；線性；微分方程；求解

引言

高等教育的大眾化，使得大學生整體素質普遍下降，近年來每況愈下。對于高職院校來說，學生基礎差尤為嚴重，由于高中數學知識掌握差缺和沒有養成好的學習習慣和方法，高等數學成為大學生學習的攔路虎，如果處理不當，將影響后續課程及專業課的學習，打擊學生的學習積極性和自信心。因此教師在高數教學過程中要注重對數學問題的歸納和總結，讓復雜的問題簡單化，易于理解，便于學生掌握和應用，幫助學生克服畏難情緒，培養學生的學習興趣，激發學生的創新思維。

1 兩個定理

從方程1的左邊結構特點和乘積的求導法則，我們假設方程的左邊乘以一個適當的函數后成為一乘積求導式子，即設想存在函數使得：

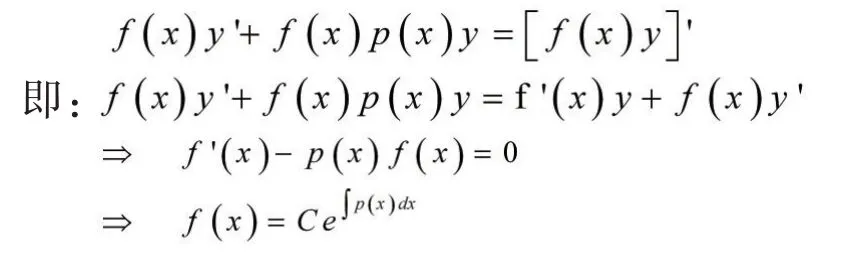
由此得到定理1.

2 應用舉例

解：利用定理1求解

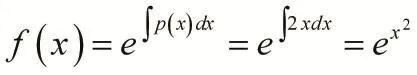
顯然，該方法省去了常數變易法必須的乘積和復合求導后再代入方程化簡的復雜過程，使問題的解決更加簡單方便。

解法一：利用常數變易法求解

通過兩種方法的對比，可以發現，利用常數變易法對非齊次線性方程的通解求導過程中，涉及到了三個函數相乘的導數和復合函數求導，是學生學習的難點，也是學生比較容易出錯的。而利用定理求解，則避免了上述求導運算，簡化了求解過程。

4 小結

兩個定理的結論簡單易記，對應的求解方法通俗易懂，省略了一些復雜的計算過程，直觀明了。高職院校基礎課程教育改革，各學科在教學中,應以增進學生創造才能為主要任務,以解決問題為主題、以學生自主活動為主要方式，加強探究性學習。教師在高等數學的教學中，應針對學生學習中存在的問題和遇到的困難，采取有效的方法，注重對數學問題的歸納和總結，讓復雜的問題簡單化，通俗易懂，便于學生掌握和應用，激發學生的學習興趣和創新性。

注釋及參考文獻：

[1]何新萌，張奕河．高等數學下冊[M]．福建:廈門大學出版社,2008:10．

[2]同濟大學數學教研室．高等數學下冊[M]．北京:高等教育出版社,2002:348．

[3]張奕河,吳小蘭．不定型極限求法研究[J]．貴陽學院學報(自然科學版),2013（2）:13-15．

On Solving Problems of First Order Non Homogeneous Linear Differential Equation

WU Xiao-lan
(Fujian Electric Vocational and Technical College，Quanzhou，Fujian 362000)

This paper presents and proves two theorems,using the two theorems for the solutions of first order non homogeneous linear differential equation.

non homogeneous;linear；differential equation；solution

O175.1

A

1673-1891（2015）01-0017-02

2014-07-29

吳小蘭（1981-），女，福建泉州人，碩士，講師，研究方向：高職數學教學和研究。