基于定子磁鏈軌跡跟蹤的優化PWM高性能閉環控制

宋文祥, 姜書豪, 阮智勇, 楊 影, 阮 毅

(上海大學機電工程與自動化學院,上海 200072)

基于定子磁鏈軌跡跟蹤的優化PWM高性能閉環控制

宋文祥, 姜書豪, 阮智勇, 楊 影, 阮 毅

(上海大學機電工程與自動化學院,上海 200072)

在低開關頻率下采用優化脈沖寬度調制(pulse width modulation,PWM)可獲得較小的諧波畸變,但將其直接應用于高性能閉環控制系統時會引起PWM波形紊亂和系統過流.給出了一組離線求解得到的特定諧波消除脈寬調制(selected harmonic eliminated pulse width modulation,SHEPWM)開關角,分析了將優化PWM應用于高性能閉環控制系統會造成系統過流的原因.深入研究了基于定子磁鏈軌跡跟蹤的優化PWM閉環控制方案,給出了一種結合SHEPWM特點的脈沖實時修正策略,實現了采用優化PWM的磁鏈軌跡跟蹤高性能控制.通過三電平逆變器異步電機驅動系統的仿真實驗驗證了該策略的有效性.結果表明,驅動系統在200～300 Hz的低開關頻率下獲得了較小的電流諧波畸變,同時具有快速動態響應能力.

優化PWM;低開關頻率;定子磁鏈軌跡跟蹤;高性能閉環控制

為降低開關損耗,提高輸出功率,一般將大功率驅動系統開關頻率限制在幾百赫茲以內.在低開關頻率下實現驅動系統的高性能控制,既能獲得理想的電流諧波畸變又具有快速響應能力,是一個具有挑戰性的課題.現有文獻報道主要有兩類解決方案：一是Geyer等[1-2]提出的長預測范圍模型預測直接控制方案,包括直接轉矩控制和直接電流控制;二是Holtz等[3-6]提出的基于磁鏈軌跡跟蹤實現優化脈沖寬度調制(pulse width modulation,PWM)閉環控制方案.模型預測直接控制方案將平均開關頻率作為價值函數,利用滾動優化策略求得最優電壓矢量,能夠充分利用有效的開關頻率.但由于產生的脈沖序列對于基波周期是異步的,從而造成電流諧波分布廣且低次諧波較多,在200～300 Hz的低開關頻率下電流諧波性能不如采用優化PWM理想[7].

優化PWM的同步對稱性可以保證在低開關頻率下獲得優越的諧波性能,但離線計算的優化PWM不能直接應用于高性能閉環控制[5-6],因此其應用基本都集中在開環的恒壓頻比(V/f)控制方面.針對機車牽引控制的特點,文獻[8]將優化PWM與矢量控制系統相結合,以實現低開關頻率下的高性能控制,但存在系統動態響應能力差和諧波性能受限的問題.實際上,傳統矢量控制和直接轉矩控制系統都無法解決采用優化PWM獲得較小諧波畸變的同時具有快速動態響應能力的矛盾[5].

早在20世紀90年代,Holtz等[9-10]提出了一種定子電流軌跡跟蹤控制方案,但電流軌跡對電機參數特別是漏感系數和瞬態定子時間常數的依賴性較高,且易受負載條件改變的影響[4-5].近年來,Holtz等[3-6]在此基礎上以定子磁鏈代替定子電流作為優化軌跡跟蹤目標,提出了定子磁鏈軌跡跟蹤控制( fl ux trajectory tracking control,FTTC)技術,實現了優化PWM高性能閉環控制.馬小亮[11-12]對該FTTC方案給出了綜述.文獻[13]以電勵磁同步電機為控制對象,研究了在低開關頻率下的優化PWM和基波觀測器,對基于FTTC的優化PWM閉環控制方案進行了探討.但磁鏈軌跡跟蹤控制方案相當復雜[8,11-12],它既不同于矢量控制,也不同于直接轉矩控制,目前國內相關研究成果較為鮮見.本工作深入研究了基于FTTC的優化PWM閉環控制方案,并給出一種結合特定諧波消除脈寬調制(selected harmonic eliminated pulse width modulation,SHEPWM)特點的脈沖實時修正策略,最后利用Matlab/Simulink建模和仿真對其有效性進行了驗證.

1 同步對稱優化PWM

1.1 三電平選擇諧波消去法

在低開關頻率下采用同步對稱的優化PWM可獲得較小的諧波畸變,常見的優化PWM策略有選擇諧波消去法(如SHEPWM)和電流總諧波最小法.本研究以SHEPWM為例,給出了采用單極性調制(包含4N個開關角)的a相輸出電壓波形(見圖1).在1/4周期內存在N個開關角,每個開關器件的開關頻率為fs=N·f1.如基波頻率為40 Hz,1/4周期(90°)內有7個開關角,則每個開關器件的開關頻率為280 Hz.

對相電壓進行傅里葉級數展開,并考慮1/4周期和半周期對稱性,輸出相電壓中不含偶次諧波與直流分量,而只含奇次正弦分量,故可表示為

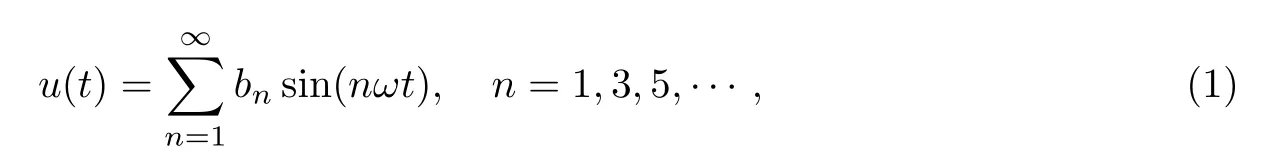
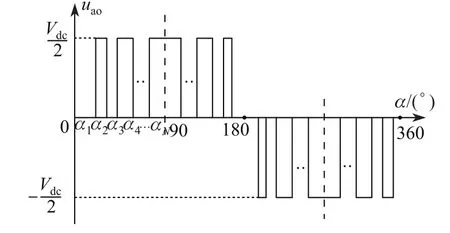
圖1 輸出相電壓PWM波形Fig.1 Waveform of output PWM phase voltage

式中,2Vdc/π對應六拍工作模式下的最大基波電壓,m∈[0,1].

由于偶次諧波自動抵消,且逆變器帶三相對稱負載時輸出電壓不含3倍次諧波,因此消除諧波時只考慮輸出電壓的非3倍次的奇次諧波(如5,7,11,···).令u1為基波電壓幅值,且期望的其他(N-1)個低階的高次諧波幅值為0,根據式(1)和(2)可得

式(3)即構成了利用1/4周期內的N個開關角度來消除N-1個選擇諧波的數學模型.當N為奇數時,n最大可取3N-2;當N為偶數時,n最大可取3N-1.由式(3)可知,SHEPWM的數學模型是一個非線性方程組,自變量以三角函數形式存在,并涉及非線性超越方程組的數值求解.利用求解得到的開關角α1～αk,由對稱性易求得其他區間和b,c相的開關角.

本研究直接利用Matlab優化工具包非線性方程求解的fsolve()函數來求解開關角[14].圖2給出了求解得到的a相在第Ⅰ個1/4周期(90°)內開關角α隨調制系數m的變化曲線.此時選擇N=7,即在1/4周期內有7個開關角.針對不同的調制系數m進行分段,形成分段同步的對稱優化SHEPWM策略,使開關頻率維持在一定的范圍內(如200～300 Hz),這里不過多討論.

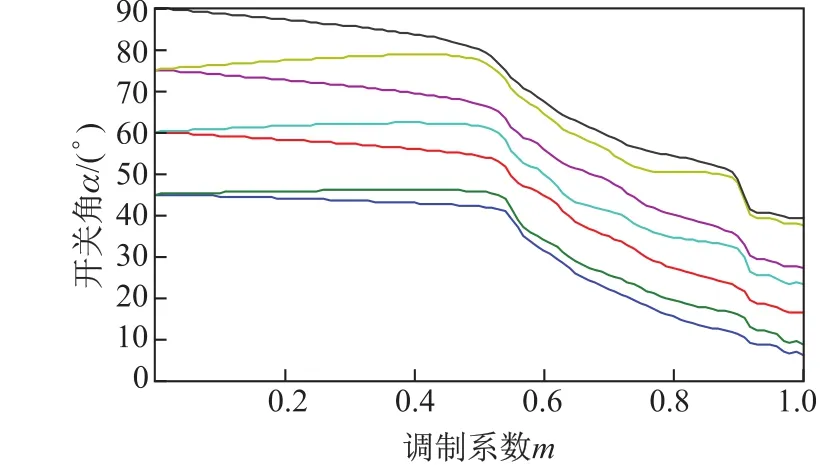
圖2 調制系數m-開關角αFig.2 Switching angle α versus the index of modulation m

1.2 同步優化PWM閉環控制存在的問題

應用優化PWM通常是將一個基波周期的開關角事先離線算好,存于控制器的脈沖模式表P(m,N)中,供工作時調用(見圖3)[3].脈沖模式表P(m,N)是調制系數m和脈沖數目N的函數,調制系數m與參考電壓矢量的幅值u?成比例,與N一起形成一對(m,N),以選擇P(m,N)中的開關角.另一輸入是參考電壓矢量的相角■u?.根據幅值u?決定調用P(m,N)表中的哪組開關角,利用其相角■u?與調用開關角αk進行比較發出開關指令.另外,利用定子角頻率ωss將開關角αk轉化為相應開關時刻tk=αk/ωss,產生的開關矢量uk作用于逆變器.

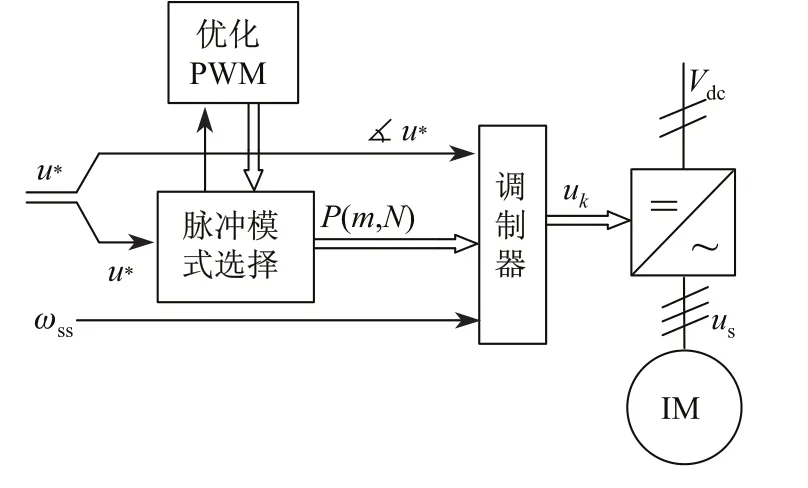
圖3 同步優化PWM控制框圖Fig.3 Block diagram of synchronous optimal PWM

通過一個基波周期內的1/4周期對稱和半波對稱,同步對稱優化PWM基于穩態離線計算出相應的開關角.這對于V/f控制比較實用,可以在一個基波周期內更換一次三角載波或采樣頻率來實現.但對于矢量控制等高性能系統,基波頻率、幅值和相位隨時都可能變化,要實現波形的同步且對稱是很困難的.隨著暫態工作點的變化,參考電壓矢量u?將立即脫離其預定軌跡趨從新的工作點,調制系數m甚至脈沖數目N都會隨之發生變化;若相應地選擇新的優化PWM模式,中途更換開關角則會引起PWM波形紊亂.

假設系統從t1時刻起工作于穩態工況1,調用P(m,N)表中P(1)組開關角,對應的PWM輸出電壓矢量為u(1)ss,沿穩態優化軌跡1運動,這里忽略電機定子繞組壓降,則工況1下的穩態定子磁鏈為

高性能閉環控制系統需要不斷更改P(m,N)表的開關角調用值,由此產生動態調制誤差.這就需要對累積的誤差進行適當處理,否則會造成磁鏈軌跡偏離穩態優化軌跡,導致電流軌跡偏離,發生系統過流.

2 基于定子磁鏈軌跡跟蹤的優化PWM閉環調速系統

2.1 定子磁鏈軌跡跟蹤控制系統

利用定子磁鏈軌跡跟蹤控制來解決高性能系統在采用優化PWM時出現的問題,其原理如圖4所示[4-5].該系統基于磁鏈軌跡跟蹤產生三相角度的修正信號ΔP,實時修正開關模式表P(m,N)中的開關角.開關角的調整也就是離線計算的優化PWM開關角的左右移位,相應的電壓伏秒積也會發生變化,而電壓伏秒積對應磁鏈,因此通過實時修正優化PWM開關角,可使實際磁鏈 ︿ψs跟隨期望的優化磁鏈ψss,從而消除動態調制誤差d(t),避免過流沖擊.

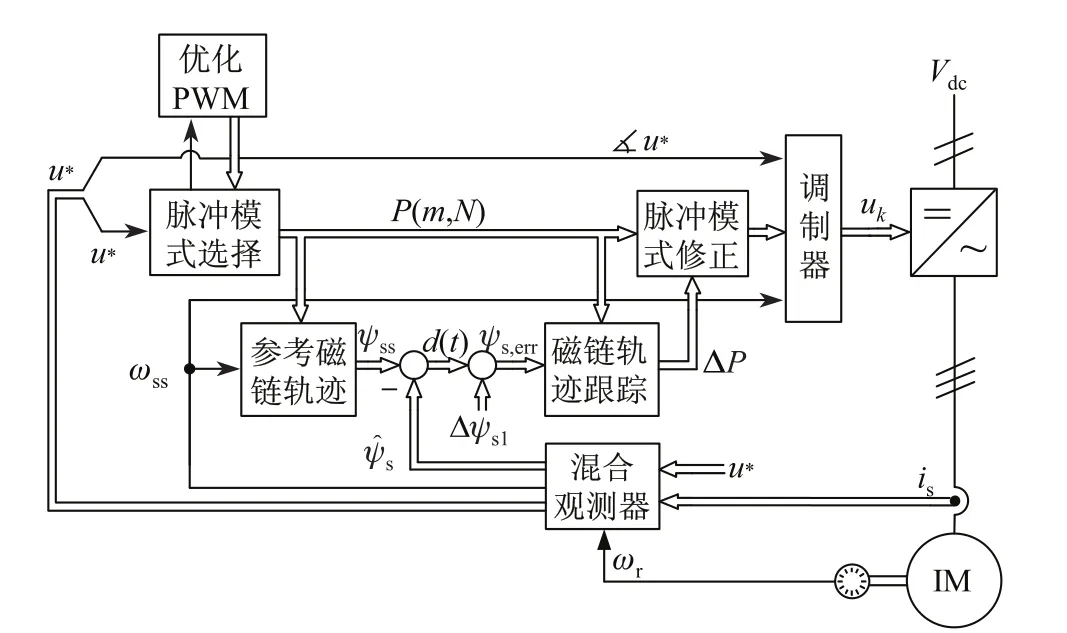
圖4 定子磁鏈軌跡跟蹤控制系統框圖Fig.4 Block diagram of stator fl ux trajectory tracking control system

不同于矢量控制,這里的PWM輸入電壓u?不是來自電流調節器輸出,而是借助混合觀測器建立的能輸出純凈無諧波的電壓u?,作為優化PWM模式的輸入.此時混合觀測器的輸入u?也不是來自電流調節器輸出,而是來自其本身輸出的u?,因此構成了一個自我封閉的穩態工作系統,輸出量都是純凈的基波值,僅在接受輸入擾動信號后才改變工作狀態,這被稱為“自控電機”模型[11-12].定子角頻率ωss用來將開關角轉化為對應開關時刻,可由混合觀測器得到.

2.2 穩態優化定子磁鏈矢量

定子磁鏈受電機參數的影響最小,在調制系數m不是很小(如m＞0.3)時可以忽略定子電阻壓降,從而使定子磁鏈與負載電流無關[5,12],因此以穩態優化定子磁鏈矢量代替定子電流矢量作為軌跡跟蹤目標.忽略定子電阻壓降,通過優化PWM電壓矢量uss的積分得到優化的穩態定子磁鏈矢量ψss,即

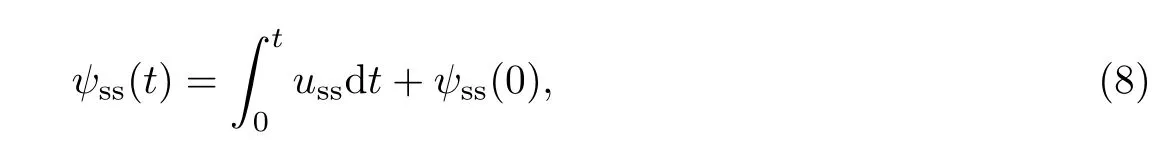
式中,積分上限由當前電壓矢量角度■u?決定,通過ωss轉化為對應時間,ψss(0)為積分初始值,且有

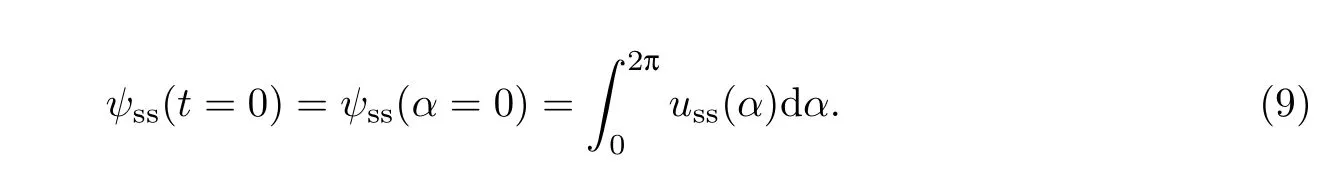
對應優化PWM的離散開關角,式(8)和(9)中的連續積分實際上就是離散求和的過程,亦即以當前開關角為上限求取PWM的電壓伏秒積.

2.3 基于自控電機的FTTC閉環調速

由圖4給出的引入自控電機模型的自我封閉系統不能調速,須通過外環加入擾動量Δψs1才能改變原來的穩態工作點.基于FTTC的閉環調速系統如圖5所示,外環由磁鏈控制器和轉速控制器(兩個PI調節器)構成,沒有電流調節器,這不同于矢量控制和直接轉矩控制系統結構.

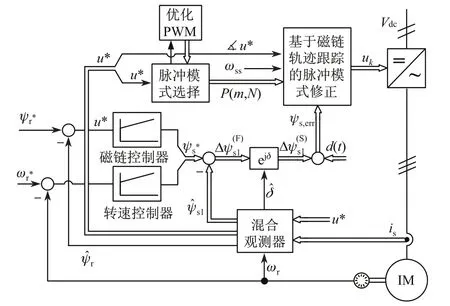
圖5 基于自控電機FTTC閉環調速系統Fig.5 Closed-loop control system of FTTC with the self-controlled motor

2.4 含自控電機模型的混合觀測器

利用電機狀態觀測器模型可以獲取控制需要的反饋量.觀測器提供的反饋信號包括輸入電壓矢量u?、定子磁鏈基波分量、定子磁鏈、轉子磁鏈(包括幅值和相位δ)、定子角頻率ωss.這些信號可分為兩組：一組是與自控電機模型相關的基波信號,包括u?和;另一組是定轉子磁鏈矢量,和定子角頻率ωss,它們不涉及自控電機模型,可直接通過電流模型或全階觀測器等傳統磁鏈估計手段獲取.若采用全階觀測器,則電壓矢量可由開關狀態重構,而不是混合觀測器的基波信號u?.與全階觀測器相比,低開關頻率下的混合觀測器具有更佳的動態性能[15].

混合觀測器將定子側模型建立在靜止坐標系下的降階觀測器,以復矢量形式表示[15]：

將轉子側模型建立在轉子磁鏈定向坐標系下：

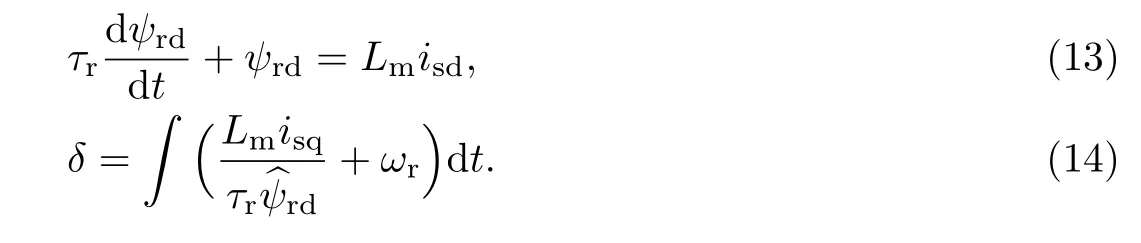
由式(13)和(14)得到轉子磁鏈的幅值ψr和位置角δ,即可得到靜止坐標系下的轉子磁鏈矢量根據定轉子磁鏈關系：

可得定子電流基波分量is1.

定子角頻率ωss可直接由轉子磁鏈位置角δ的微分得到,這是一個緩慢的平滑信號.純凈的基波電壓矢量信號u?同時作為觀測器的輸出,即

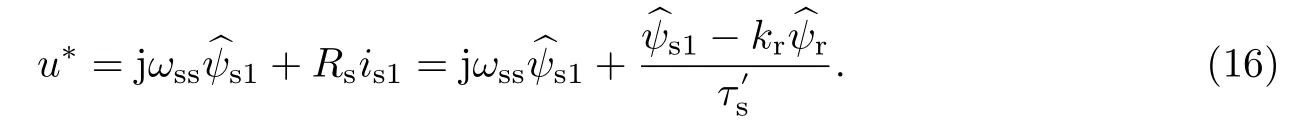
因此,含自控電機模型的估計電機狀態和基波分量的混合觀測器如圖6所示.

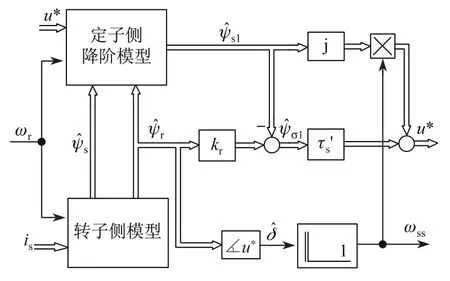
圖6 含自控電機模型的混合觀測器Fig.6 Hybrid observer with the self-controlled motor model

2.5 基于磁鏈軌跡跟蹤的脈沖模式實時修正

考慮利用優化PWM模式在采樣周期Ts內的開關時刻移位來補償總磁鏈偏差優化PWM處于不同位置時,對開關角的左右移位造成的磁鏈修正效果不一樣.圖7為脈沖修正帶來的磁鏈修正示意圖,此時脈沖模式對應的開關時刻位于正半周期內,向左移動時Δtai＜0,磁鏈減小;向右移動時Δtai＞0,磁鏈增大.在時刻,脈沖由Vdc/2跳變到0,若脈沖由0跳變到Vdc/2,將產生相反的磁鏈修正效果.若開關時刻位于負半周,則效果亦然.

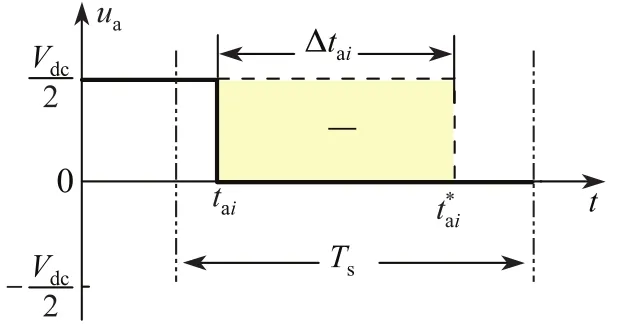
圖7 相電壓脈沖調整形成的磁鏈修正Fig.7 Phase voltage adjustment showing e ff ect of fl ux error correction

優化PWM模式動態調整帶來磁鏈變化的普遍規律總結如下.

(1)若給定換相時刻txi使相電壓增大(即-Vdc/2→0或0→Vdc/2),則記為sign(Δuxi)= 1.若跳變時刻推后,Δtxi＞0,伏秒積減小;若跳變時刻提前,Δtxi＜0,伏秒積增大.

(2)若給定換相時刻txi使相電壓減小(即Vdc/2→0或0→-Vdc/2),則記為sign(Δuxi)= -1.若跳變時刻推后,Δtxi＞0,伏秒積增大;若跳變時刻提前,Δtxi＜0,伏秒積減小.

(3)若在采樣周期Ts內不存在跳變,則記為sign(Δuxi)=0.

綜上,開關跳變對磁鏈的影響可統一表示為

具體而言,對于a相1/4周期內有N個開關角,一個基波周期內有4N個開關角,記為i=1,2,···,4N.結合N=7的SHEPWM特點,根據當前開關角所處的位置,可確定開關序列uss的值：

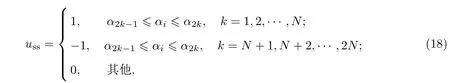
于是,sign(Δuai)可以確定為

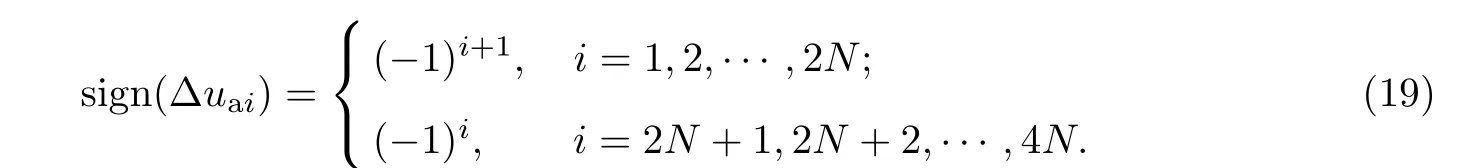
開關角調整對磁鏈的影響可表示如下：

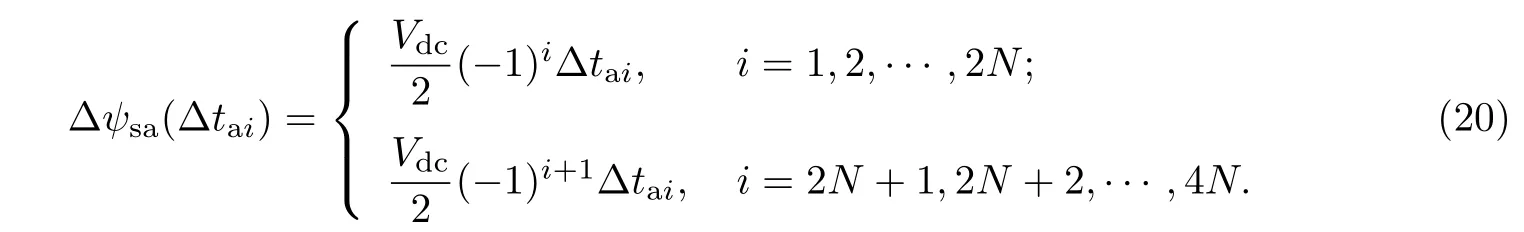
假設電壓矢量u?所在的位置角為■u?,則其對應的開關時刻為■u?/ωss.考慮下一個采樣周期到時刻,根據磁鏈偏差對Ts時間范圍內的開關角進行調整.由于每相可能會存在多次跳變,因此考慮采樣周期內對應約10°范圍,以保證該范圍內至少有1～2次開關角切換.值得指出的是,開關時刻的修正不是隨意的,必須受限于當前時刻kTs和同相相鄰開關時刻.

圖8為開關時刻的調整示意圖.在采樣周期Ts內,a相的第一個開關時刻受限于kTs和b相的第二個開關時刻因此a相的第二個開關時刻只能被提前到,也僅僅可被延遲至第三個開關時刻;b,c相開關時刻的調整存在類似的約束限制.值得注意的是,b相在采樣周期內有3個開關時刻,在此僅考慮對其前2個開關時刻,進行調整.

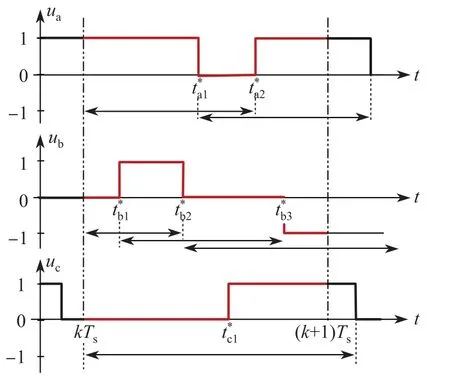
圖8 開關時刻調整示意圖Fig.8 Diagram of the switching instants correction

對a相而言,開關角度修正量為

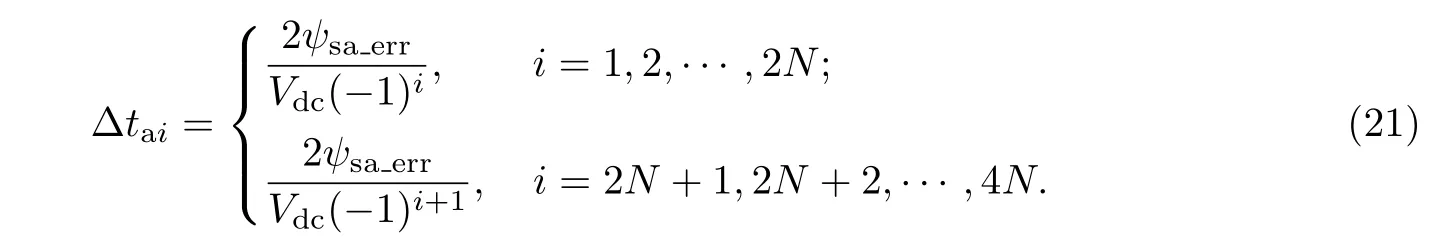
3 仿真研究

針對一臺4 kW異步電機驅動系統,結合本工作提出的驅動脈沖實時修正策略,利用Matlab/Simulink建立了磁鏈軌跡跟蹤控制系統仿真模型.系統采樣周期Ts=500μs,主電路采用中點箝位式三電平逆變器,驅動系統相關額定值及參數如表1所示.

圖9給出了電機在40 Hz下由空載切換至額定負載時的電流isa、轉速ωr和轉矩Te的波形.可以看到,突加負載時電流波形過渡較為平滑,沒有發生過流現象;轉速ωr在加載瞬間先有小的跌落,隨后較快地穩定在1 200 r/min轉速平穩運行;電機轉矩大約經過十幾ms達到給定值,轉矩響應也較為快速.可見所建立的磁鏈軌跡跟蹤閉環系統具有較好的動態響應性能.

圖10為電機在40 Hz下由空載切換至額定負載時d-q軸電流is(d,q)及其基波分量is1(d,q).可以看到,加載時q軸電流相應變大,d軸電流略有波動,二者耦合程度較低,基波電流能更清晰地反映這一現象.這說明閉環調速系統在低開關頻率下能夠實現對d軸和q軸電流的獨立控制.

表1 驅動系統額定值及參數Table 1 Rated values and parameters of drive system

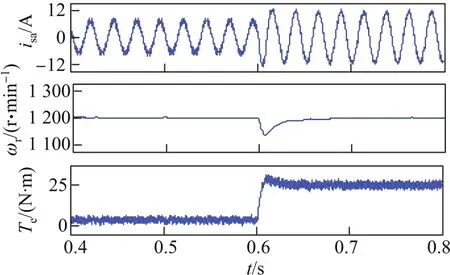
圖9 電機由空載切換至額定負載時的動態波形Fig.9 Dynamic waveforms with rated load command

圖10 突加額定負載時電流is(d,q)及其基波分量is1(d,q)Fig.10 Current waveforms and its fundamental components with step rated load command

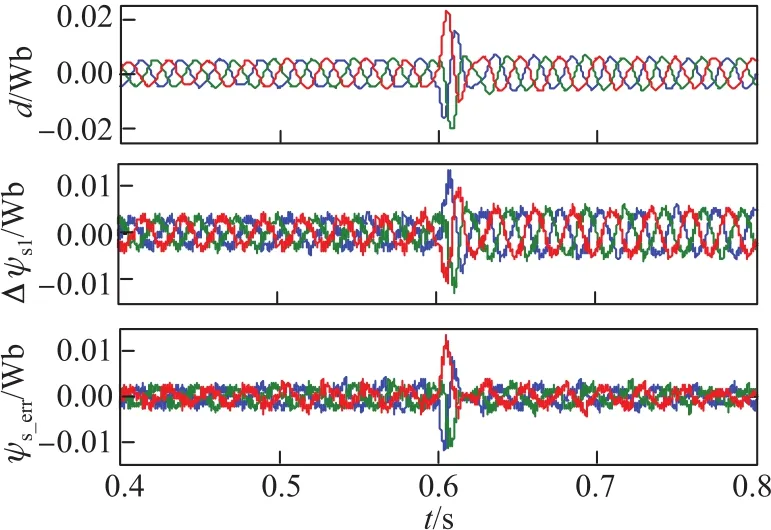
圖11 定子磁鏈偏差d,Δψs1和ψserrFig.11 Tracking error of stator fl ux vector

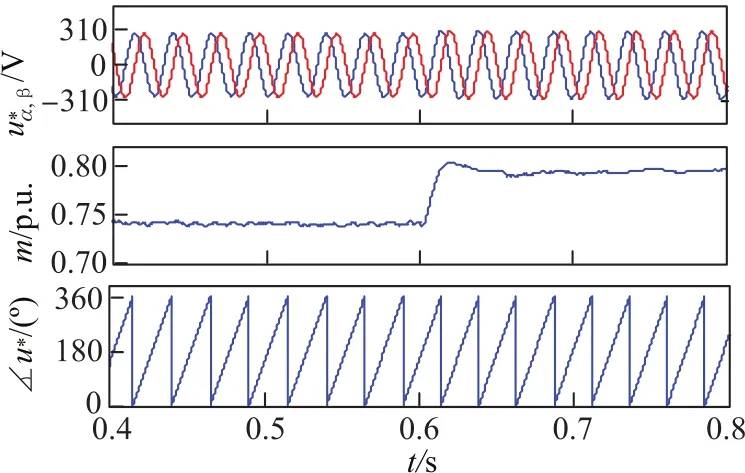
圖12 基波電壓、調制系數m和矢量角Fig.12 Fundamental voltage,index of modulation and angle of voltage vector

圖13給出了加載后一個周期內離線計算SHEPWM(藍色實線)和調整后的PWM(紅色虛線)開關序列波形.此時SHEPWM的脈沖數目N=7,即電機運行在40 Hz時三電平逆變器的開關頻率為280 Hz.可以看到,加載后三相電壓進行了局部調整,調整后的開關角度基本保持了原來的對稱性.

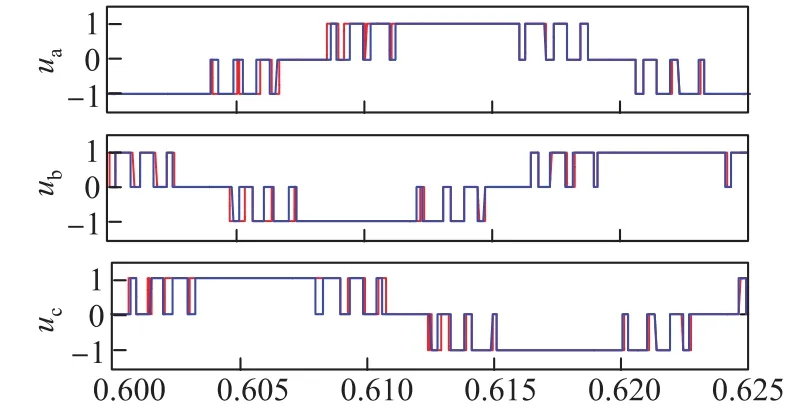
圖13 調整前后的開關序列Fig.13 Original and corrected switching sequences

圖14為電機帶額定負載穩定運行時三相電流is及其中a相電流isa的諧波頻譜.可以看出：三相電流基本對稱,電流毛刺小;a相電流總諧波畸變率只有3.86%,維持在相當低的水平.這表明閉環驅動系統在低開關頻率(此時為280 Hz)下運行獲得了良好的諧波性能.

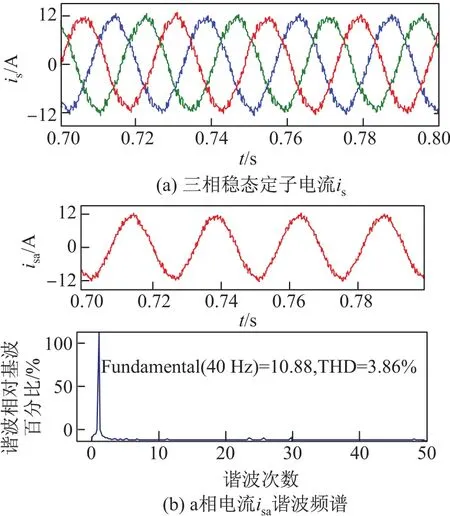
圖14 三相穩態電流is及其a相電流isa諧波頻譜Fig.14 Stator current isand harmonic spectrum of isa

圖15為電機帶額定負載運行時的定子電流軌跡和定子磁鏈軌跡,其中圖(a)為加載前后一個周期內的動態電流軌跡,圖(b)和(c)為穩態運行時一個周期內的電流和磁鏈軌跡.很明顯,加載時電流軌跡切換平穩、響應快,沒有過流現象;穩態運行時電流軌跡對稱、波動小,磁鏈軌跡接近單位圓.由此可推斷電機在低開關頻率下運行狀態良好.

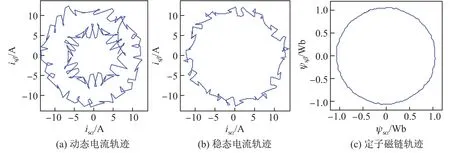
圖15 定子電流軌跡和定子磁鏈軌跡Fig.15 Trajectories of stator fl ux and stator current

4 結束語

本工作深入研究了基于定子磁鏈軌跡跟蹤控制的優化PWM閉環控制方案,提出一種結合SHEPWM特點的優化脈沖實時修正策略,實現了基于磁鏈軌跡跟蹤的優化PWM高性能閉環控制.仿真結果表明,異步電機驅動系統在200～300 Hz的低開關頻率下獲得了較小的諧波畸變,同時具有快速動態響應能力.

本工作所研究的系統方案既不同于常規矢量控制,又不同于直接轉矩控制,是電機高性能調速方案的一個發展.該方案可向其他多電平逆變器拓撲驅動交流電機這一大類系統擴展,對中高壓大功率驅動系統在低開關頻率下的高性能控制具有指導性意義.

[1]GEYER T,PAPAFOTIOU G,MORARI M.Model predictive direct torque control—part I：concept, algorithm and analysis[J].IEEE Transactions on Industrial Electronics,2009,56(6)：1894-1905.

[2]GEYER T.Model predictive direct current control：formulation of the stator current bounds and the concept of the switching horizon[J].IEEE Industry Applications Magazine,2012,18(2)：47-59.

[3]HOLTz J,OIKONOMOU N.Synchronous optimal pulsewidth modulation and stator fl ux trajectory control for medium-voltage drives[J].IEEE Transactions on Industry Applications,2007,43(2)：600-608.

[4]OIKONOMOU N,HOLTz J.Closed-loop control of medium-voltage drives operated with synchronous optimal pulsewidth modulation[J].IEEE Transactions on Industry Applications,2008, 44(1)：115-123.

[5]HOLTz J,OIKONOMOU N.Fast dynamic control of medium voltage drives operating at very low switching frequency—an overview[J].IEEE Transactions on Industrial Electronics,2008,55(3)：1005-1013.

[6]HOLTz J,QI X.Optimal control of medium-voltage drives—an overview[J].IEEE Transactions on Industrial Electronics,2013,60(12)：5472-5481.

[7]GEYER T.A comparison of control and modulation schemes for medium-voltage drives：emerging predictive control concepts versus PWM-based schemes[J].IEEE Transactions on Industry Applications,2011,47(3)：1380-1389.

[8]孫大南.地鐵車輛牽引電驅動系統控制關鍵技術研究[D].北京：北京交通大學,2012.

[9]HOLTz J,BEYER B.The trajectory tracking approach—a new method for minimum distortion PWM in dynamic high-power drives[J].IEEE Transactions on Industry Applications,1994, 30(4)：1048-1057.

[10]HOLTz J,BEYER B.Fast current trajectory tracking control based on synchronous optimal pulsewidth modulation[J].IEEE Transactions on Industry Applications,1995,31(5)：1110-1120.

[11]馬小亮.概述低開關頻率PWM變頻的問題及解決辦法[J].電氣傳動,2009,39(5)：3-9.

[12]馬小亮.低開關頻率中壓傳動的定子磁鏈軌跡跟蹤控制綜述[J].變頻器世界,2009,12：45-51.

[13]符曉.電勵磁同步電機低開關頻率控制技術研究[D].徐州：中國礦業大學,2011.

[14]費萬民,張艷莉,阮新波,等.三電平逆變器SHEPWM非線性方程組的求解[J].中國電機工程學報, 2008,28(6)：62-68.

[15]HOLTz J,OIKONOMOU N.Estimation of the fundamental current in low-switching-frequency high dynamic medium-voltage drives[J].IEEE Transactions on Industry Applications,2008, 44(5)：1597-1605.

本文彩色版可登陸本刊網站查詢：http：//www.journal.shu.edu.cn

High performance close-loop control of optimal PWM based on stator fl ux trajectory tracking

SONG Wen-xiang, JIANG Shu-hao, RUAN Zhi-yong, YANG Ying, RUAN Yi
(School of Mechatronics Engineering and Automation,Shanghai University,Shanghai 200072,China)

Lower harmonic distortion at low switching frequency requires optimal pulse patterns.But it cannot be directly used in high performance systems.A stator fl ux trajectory tracking control(FTTC)system is studied,and a pulse width modulation(PWM) correction method is proposed.Based on this method,dynamic modulation errors and high overcurrents as the operating conditions change are discussed.Furthermore,high performance closed-loop control of optimal PWM based on FTTC with a self-controlled machine model can be realized.Simulation results show that both fast dynamic response and low harmonics characteristic can be achieved at a low switching frequency of 200～300 Hz.Its harmonic characteristic is more outstanding than that of model predictive direct control methods.

optimal PWM;low switching frequency;stator fl ux trajectory tracking; high performance closed-loop control

TM 343

A

1007-2861(2015)01-0128-13

10.3969/j.issn.1007-2861.2014.03.021

2014-04-08

國家自然科學基金資助項目(51377102);臺達環境與教育基金會“電力電子科教發展計劃”資助項目(DREG2013009)

宋文祥(1973—),男,副教授,博士,研究方向為電機驅動控制及應用、新型電力電子變換.

E-mail：wxsong@shu.edu.cn