分布式光伏在上海國家會展中心節能改造中的應用

高文偉，李慶來，賀青龍，邱慧芳[.上海東浩蘭生國際服務貿易（集團）有限公司，上海　00040；.上海東浩諾蘭生智慧科技有限公司，上海　0007]

近年來，中國光伏裝機容量逐年增長，見圖1。截至2016 年底，上海市光伏發電項目裝機容量已突破 30萬kW，項目涵蓋工廠、商業、醫院、學校、家庭等。在上海開展太陽能光伏工程項目過程中，也經常受到以下一些條件限制：土地資源緊張；高樓林立，空間條件限制；擁有屋頂產權的業主積極性不高；光伏項目合同期長，容易發生業主變更等情況；項目建設投資方融資困難。盡管受種種因素限制，但考慮到上海國家會展中心屋頂面積大、周邊遮擋少、平均電價貴、節能服務公司資金雄厚等眾多優勢，分布式光伏發電項目必將為后續節能減排工作起到示范作用。

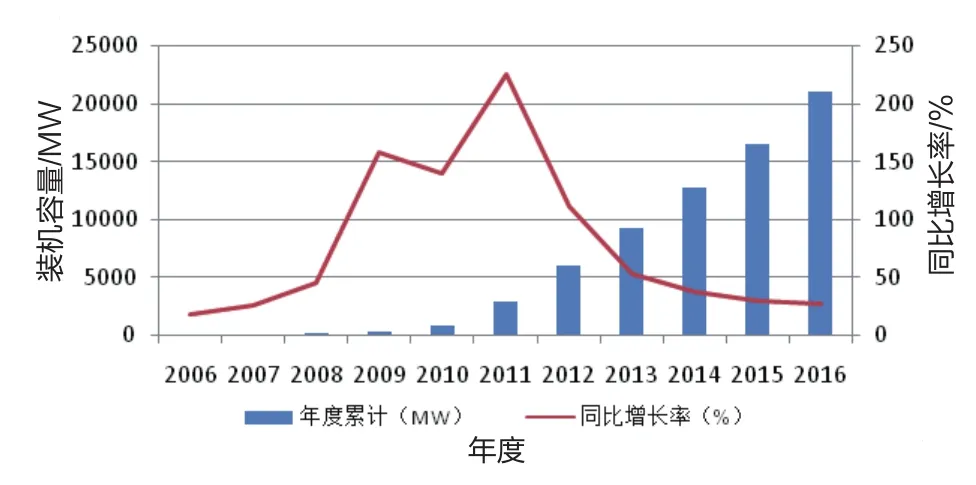
圖1　中國光伏裝機容量統計

1　光伏系統分類、構成及運行方式

1.1　光伏發電工程分類

目前上網型太陽能光伏發電工程的形式主要有：光伏建筑一體化(BIPV)、地面太陽能發電場、屋頂太陽能發電系統(BAPV)。

(1) 光伏建筑一體化。光伏發電系統以建筑材料的形式作為建筑的一部分，通常為建筑屋頂和光照條件較好的建筑立面，發電多為建筑自用。

(2) 地面太陽能發電場。利用地面專門的場地建設光伏發電系統。

(3) 屋頂太陽能發電系統。利用現有建筑的閑置屋頂，一般需要較大面積且朝向較好的建筑物屋頂。與其他光伏發電系統相比，屋頂太陽能光伏發電系統具有不占專門用地面積、可選光伏組件多、組件安裝方式比較自由、維護方便等突出優點，尤其適合在工商業發達，缺乏可供開發利用空地的地區大規模推廣應用。

1.2　光伏系統構成

(1) 太陽能電池是把太陽能轉化成電能的最主要組件。商用的太陽能電池主要有以下幾種類型：單晶硅電池、多晶硅電池、非晶硅電池、碲化鎘電池、銅銦鎵硒電池等，各類型主要性能參數見表1。

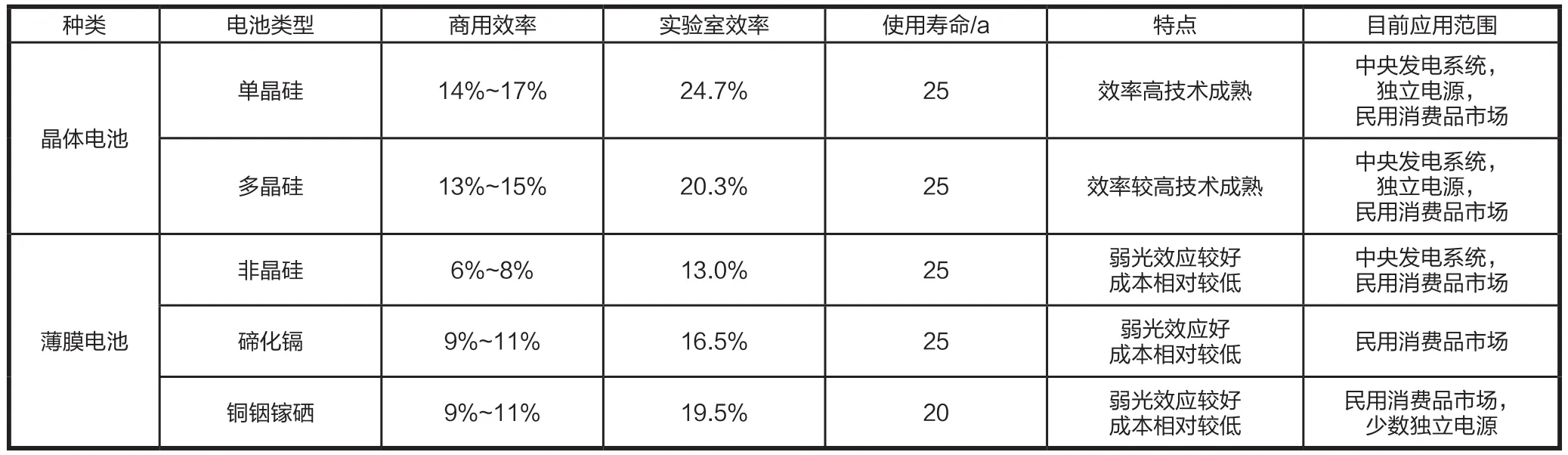
表1　太陽能電池性能參數比較

(2) 蓄電池的作用是儲存太陽能電池方針受光照時所發出的電能，向負荷供電。光伏發電系統對所用蓄電池的基本要求是：自放電率低、使用壽命長、深放電能力強、充電效率高、少維護或免維護、工作溫度范圍寬、價格低廉。目前我國與太陽能發電系統配套使用的蓄電池主要是鉛酸蓄電池。

(3) 充放電控制器用以防止蓄電池過充電或過放電，是光伏發電系統的核心部件之一。充放電控制器一般應具有如下功能：信號檢測、蓄電池最優充電控制、蓄電池放電管理、設備保護、故障診斷定位、運行狀態指示等。

(4) 并網逆變器是并網光伏發電系統的核心部件，與獨立逆變器不同，它不僅要將太陽能光伏發電系統發出的直流電轉換成交流電，而且要對交流電的頻率、電壓、電流、相位、同步等進行控制。還必須具備以下功能：自適應調節電能質量、最大功率跟蹤技術(MPPT)、防止“孤島效應”、數據遠傳功能、較高工作效率及可靠性等。

1.3　光伏系統運行方式

太陽能光伏發電系統的運行方式分為獨立運行方式和并網運行方式，并網光伏發電系統又分為分散式小型并網光伏發電系統和集中式大型并網光伏發電系統。

分散式小型并網光伏發電系統的主要特點是所發的電能直接分配到用電負荷上，多余或不足的電力通過連接電網來調節。分散式又可分為可逆流和不可逆流兩大類。可逆流系統在光伏發電系統產生剩余電能時將該電能送入電網，光伏發電系統的發電量始終小于或等于用戶的用電量，電能不夠時由電網提供。這種系統不會出現光伏發電系統向電網送電的情況。

集中式大型并網光伏發電系統是將太陽能光伏發電系統的電力通過逆變器并入公用電網，把公用電網作為光伏發電系統的載體，與公用電網實現高品質的電能傳輸。

2　國家會展中心光伏發電系統

2.1　屋面光伏布置

上海國家會展中心總建筑面積 147 萬 m2，其中擁有18 萬 m2辦公設施，本光伏發電項目只利用了部分辦公樓屋頂面積，共計 3 萬 m2左右。根據項目實際情況綜合考慮光伏組件效率、技術成熟性、綜合性價比以及采購訂貨周期等，本工程推薦選用多晶硅光伏組件規格 265 Wp，尺寸為1 650 mm×882 mm×35 mm。

考慮盡可能小地影響建筑視覺效果，本項目光伏組件擬采用 10°傾角固定式安裝。單個屋面的光伏組件數量總計為 2 728 塊，整個項目光伏總裝機容量 2 168 kW。

2.2　運行方式及接入方案

上海國家會展中心當前電力供應來自上海電網，配備110 kV 降壓站，在各建筑單體內設置有 10 kV 變電站，設有 UPS 不間斷供應。3 個辦公單體內設置 8 MVA 10/0.4 kV 降壓變壓器。

本次光伏發電項目采用分散式小型并網光伏發電系統，總裝機容量 2 168 kW，每個區域選用組串式并網逆變器將直流轉變為交流，接至該區域 10 kV 變壓站的400 V 母線，總共設置 400 V 接入點 6 個，每個接入容量為 361.46 kW，光伏發電量基本能自行消納。組串式并網逆變器在室外掛墻安裝，額定容量為 50 kW，最大轉換效率≥99%，根據低壓總開關柜額定電流計算 361.46/(1.732×0.4)=521.74 A，選用 MNS 型低壓抽出式開關柜，其額定電流 630 A。

2.3　發電量及項目投資概算

2.3.1發電量估算

影響光伏發電量的關鍵因素是系統效率，系統效率主要考慮的因素有：灰塵、雨水遮擋的功率損耗、直流交流部分線纜功率損耗、變壓器功率損耗、跟蹤系統的精度等，設定光伏發電系統整體效率 80%。

根據上海市全年太陽總輻射量 4 570 MJ/m2計算，折合標準日照條件(1 000 W/m2)下的日照峰值小時數總計為1 270 h。

(1) 年發電利用小時數(發電當量小時數)初始值為：1 270×80%(系統效率)＝1 016 h ；

(2) 本工程系統構成：2.168 MWp 晶體硅組件固定安裝；

(3) 光伏組件光電轉換效率逐年衰減，整個光伏發電系統 25 a 壽命期內平均年有效利用小時數也隨之逐年降低；

(4) 本項目擬采用的光伏組件的光電轉換效率衰減速率為：首年衰減不超過 2.5%，10 a 衰減不超過 10%，25 a衰減不超過 20%；

(5) 第 N 年發電量=初始年發電量×(1-N×組件衰減率)。

計算可知，25 a 總發電量達 4 883 萬 kW·h，該項目年平均發電量 195.3 萬 kW·h，每年可為電網節省標煤約 595 t，減排 CO2約 1 590 t，減排大氣污染物 SO2約12.1 t， NOx約 4.1 t。

2.3.2項目投資概算

項目投資概算具體情況見表2。

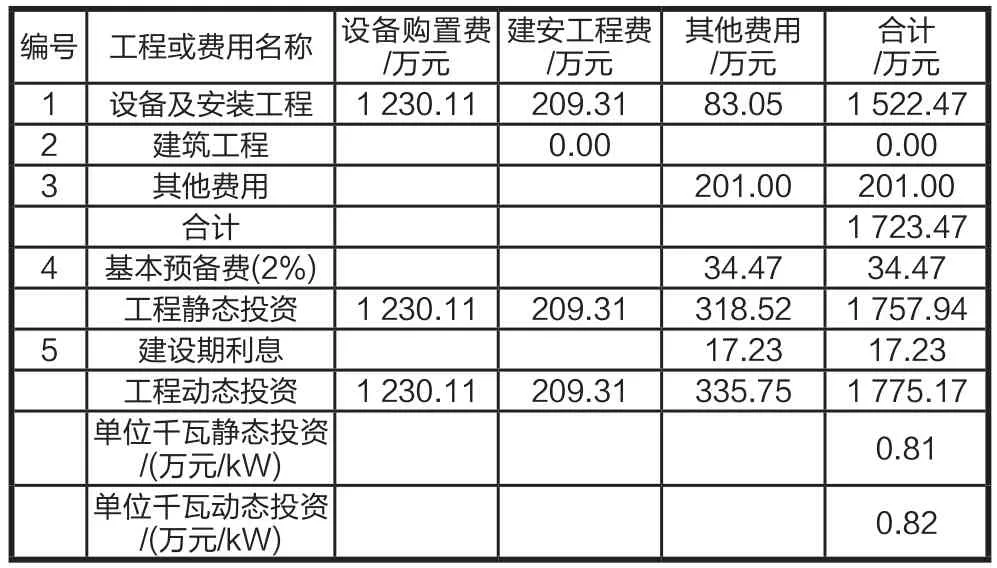
表2　總概算表

2.4　發電效益計算

光伏發電時間按照 9 點至 15 點考慮，光伏發電全部自用，對應企業電價為峰值電價和平段電價，取其平均值 0.9元/kW·h 電作為計算基準，前 20 a 發電電價享受國家 0.42元/kW·h 的補貼。前 20 a 自發自用電價為 0.9+0.42=1.32元/kW·h，第 21～25 a 自發自用電價為 0.9 元/kW·h。

本項目應交納的稅金包括所得稅，所得稅按應納稅所得額計算，本項目的應納稅所得額為發電收入扣除成本后的余額，所得稅按 25% 征收。根據《中華人民共和國企業所得稅法實施條例》及《公共基礎設施項目企業所得稅優惠目錄》規定，太陽能發電新建項目可以享受“三免三減半”的企業所得稅優惠政策。通過對上述光伏發電量及發電收入計算，以工程建設(EPC)模式執行，預計本項目靜態投資回報期為 7 a左右。

3　結　語

(1) 分布式光伏發電作為既有建筑節能減排的有效途徑之一，在國家及上海市相關政策及資金支持下，在上海市已經取得了廣泛的推廣。

(2) 公共建筑一般的用電高峰與太陽能光伏輸出的清潔能源同步，同時可以自行消納，因此在上海國家會展中心推廣實施光伏發電工程項目，不僅具有實實在在的經濟收益，更起到了示范引領的作用。

(3) 本項目由上海電氣建筑節能有限公司于 2016 年 11月完成施工圖設計，2017 年 2 月項目施工完成。

(4) 2017 年 4 月，6 個并網接入點全部完成電力公司計量表計安裝。截至當前，2.168 MW 光伏發電項目已累計為上海國家會展中心提供了 20 萬 kW·h 綠色能源。