前輪主銷間隙對汽車蛇行工況下穩定性的影響

蔣亦斌+魏道高+王鵬+潘之杰+肖懷陽

摘 要：主銷間隙是影響汽車蛇行工況下穩定性的重要參數。將轉向機構簡化為平面連桿機構，并就機構中轉向節主銷與襯套間隙對蛇形工況下汽車穩定性的影響進行分析。考慮以上間隙建立了四自由度車輛操縱運動系統數學模型，基于該模型，應用數值分析方法對間隙參數變化時樣車質心側偏角的穩定性進行仿真分析。結果表明，間隙參數變化時車輛蛇行動力學行為表現為由倍周期進入單周期、混沌，然后從倍周期回到單周期。隨著間隙的增大，汽車蛇行失穩的上臨界頻率幾乎無變化，但下臨界頻率逐漸加大，失穩頻率帶寬也相應加大，且混沌區域的窗口動力學特性有明顯差異。

關鍵詞：主銷間隙；平面連桿機構；蛇行；動力學行為；混沌

中圖分類號：U463.46文獻標文獻標識碼：A文獻標DOI：10.3969/j.issn.2095-1469.2015.03.06

蛇行工況是汽車行駛過程中一種常見工況，在道路交通中時有事故出現[1-3]，因此國內外學者對其展開較廣泛而深入的研究。文獻[4]運用VEDYNA建立了樣車模型，并運用硬件在環試驗進行了蛇形工況仿真，分析了汽車質心位置對蛇行工況穩定性的影響，得出過高的質心位置會使汽車運動穩定性變差，使其可能在蛇行行駛工況時發生側翻。文獻[5]建立了電動輪獨立驅動汽車的多自由度系統模型，通過變速度的汽車蛇行工況試驗，分析得出了行駛速度對汽車蛇行工況行駛穩定性的影響。文獻[6]建立了二自由度汽車系統模型，進行了不同幅值的轉向盤正弦輸入仿真試驗，通過相平面分析，得出過高的正弦轉向幅值會使汽車蛇行工況行駛穩定性變差。文獻[7]建立了二自由度汽車系統模型，進行了不同周期的轉向盤正弦輸入仿真試驗，得出了轉向盤正弦輸入頻率對汽車蛇行工況行駛穩定性有較大的影響。文獻[8]建立了多自由度的汽車路面系統模型，分別對二自由度、三自由度及四自由度系統模型進行蛇行工況仿真試驗，對比樣車道路試驗結果，得到了三自由度及四自由度汽車路面系統模型能更好地反映汽車蛇形工況的結論。文獻[9]建立了考慮四輪定位參數的汽車四自由度操縱穩定性模型，運用數值仿真分析，得到了四輪定位參數對汽車蛇行工況穩定性的影響。文獻[10]～[12]針對不同的汽車系統模型，提出了多種汽車行駛穩定性控制策略，通過蛇行工況仿真試驗，證明這些針對車輪滑移率、質心側偏角及橫擺角速度的控制策略能夠有效地提高汽車蛇行工況行駛穩定性。

綜上分析可見，以上學者的研究多是關于工況參數（如行駛速度v和方向盤轉向角δ）、汽車質心位置及控制策略對蛇行穩定性的影響，而轉向系間隙對汽車蛇行工況頻率特性的影響未被重視，正如文獻[13]寫道：“至今很難見到論述轉向系間隙影響汽車操縱運動文獻”。而我們前期研究表明間隙對操縱運動的影響不可忽略[14]。

因此，本文在以上學者研究成果以及我們前期研究的基礎上，考慮轉向節主銷與襯套間隙非線性因素，建立了含車身側傾運動的四自由度汽車轉向行駛非線性動力學模型。對該模型進行數值計算與分析，以獲得轉向節主銷與襯套間隙因素對汽車蛇行工況下頻率特性的影響，尋找間隙影響蛇行穩定性的規律，進一步豐富汽車轉向行駛工況非線性動力學理論。

1 含主銷間隙轉向行駛系統動力學模型

1.1 考慮間隙的系統力學模型

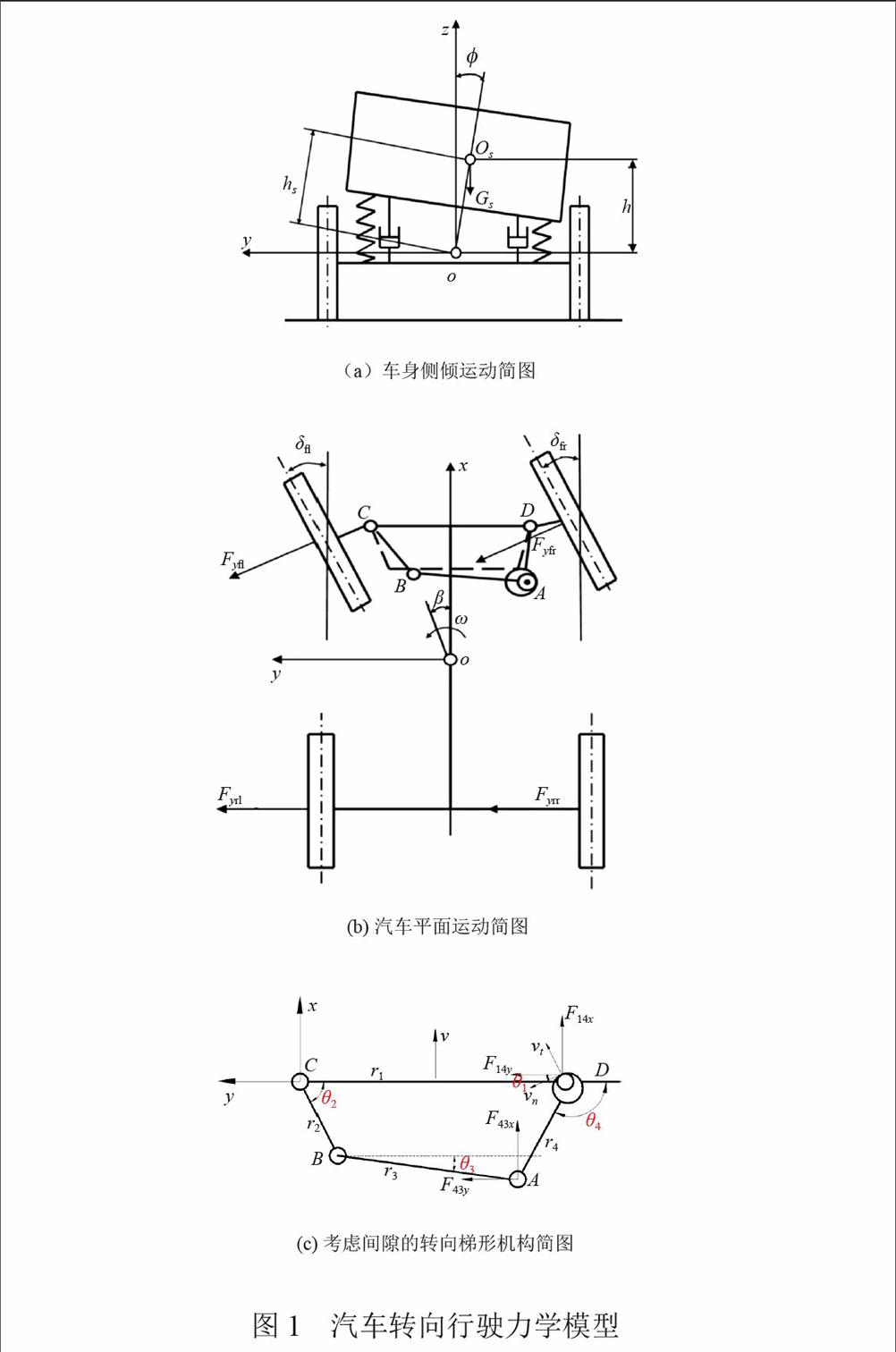
在前人建立的汽車轉向行駛系統力學模型的基礎上，本文考慮轉向節主銷與襯套間隙對轉向穩定性的影響，建立樣車轉向系統力學模型和坐標系如圖1（a）、（b）、（c）所示。

由于考慮主銷間隙，忽略前輪定位參數影響，將樣車的轉向梯形機構簡化為曲柄連桿機構[15-16]，如圖1（c）所示。為簡化分析過程僅考慮轉向節主銷與襯套間隙，桿件均看作剛體。汽車以速度v做等速蛇行行駛，oxyz為固定于側傾中心的坐標系，xoy與路面平行，x軸指向汽車行駛方向，z軸鉛垂向上，y軸按右手定則指向左側。

該系統力學模型做如下假設：

（1）不計空氣阻力。（2）忽略前輪定位參數影響，轉向梯形機構與xoy坐標平面平行。（3）車輛前后懸架側傾中心相同。

汽車轉向行駛系統，用4個自由度表示：橫擺角速度ω，質心側偏角β，車身側傾角，左前輪轉向角δl。

1.2 含主銷間隙車輛轉向行駛運動微分方程

根據圖1（a）、（b）、（c）車輛轉向行駛力學模型，運用達朗貝爾定理，建立車輛轉向行駛整車運動微分方程。

1.2.1 車輛轉向行駛運動方程

（1）整車繞z軸力矩平衡方程

（2）整車沿y軸力平衡方程

。

（3）車身繞x軸側傾力矩平衡方程

。

（4）前從動輪（右）繞主銷的力矩平衡方程

。

式中，Fyfl為左前輪側偏力，N；Fyfr為右前輪側偏力，N；Fyrl為左后輪側偏力，N；Fyrr為右后輪側偏力，N；δr為右前輪轉角，rad；lf為前軸距，m；lr為后軸距，m；m為整車質量，kg；ms為簧上質量，kg；hs簧上質量質心到側傾軸線距離，m；Ix為簧上質量繞x軸轉動慣量，kg·m2；Ixz為簧上質量繞x、z兩軸慣性積，kg·m2；Iz為整車繞z軸轉動慣量，kg·m2； Cφ為車身側傾角阻尼，N·m·s /rad；kφ為車身側傾角剛度，N·m/rad；Jc為右梯形臂繞右側主銷的轉動慣量，kg·m2；Dw為回正力臂，m；MP間隙對主銷碰撞力矩，N·m；為右梯形臂的轉動角加速度，rad/s2。

1.2.2 輪胎側向力表達式

（1）汽車輪胎側向力選用文獻[17]簡化的魔術公式

。

其中

式中，B、C、D、E分別對應為側向力魔術公式中的剛度因子、形狀因子、峰值因子和曲率因子；a1、a2 、a3、a4 、a5、a6、a7、a8為由試驗擬合得到的參數；FZ為輪胎所受載荷，N；為輪胎側偏角，rad。由輪胎側向力表達式和表1可得樣車輪胎側向力Fy關于側偏角的關系圖，如圖2所示。

（2）前后輪的側偏角表達式

（3）車輛轉向行駛時，左右車輪載荷轉移表達式

前橋左輪載荷

前橋右輪載荷

后橋左輪載荷

后橋右輪載荷

1.2.3 轉向梯形間隙碰撞力矩求解

根據圖1（c）車輛轉向行駛時轉向梯形機構簡化力學模型，求解轉向節主銷與襯套間隙碰撞力矩。圖1（c）中的右球頭間隙碰撞模型選用二狀態間隙碰撞模型，設間隙e沿x、y軸的分量分別為ex、ey，汽車直線行駛時轉向梯形底角為。由其幾何關系可得：

。

式中，；；，

r1為左右主銷之間的水平距離；r2為左轉向梯形臂長度，m；r3為右轉向梯形臂長度，m；r4為橫拉桿長度，m；2、3、4分別為左梯形臂、橫拉桿、右梯形臂和y軸所成的角度，rad。

設接觸角1由下式表示：

設間隙中軸銷相對于軸套的法向速度和切向速度分別為vn、vt。

。

引入符號函數

間隙運動副碰撞力法向力Fn與切向力Ft分別為

。

式中，；K為間隙處軸套表面剛度，

N/m；f為間隙處軸套表面摩擦系數；r為間隙，m； Cn為間隙處軸套表面法向阻尼系數，N·s/m；Ct為間隙處軸套表面切向阻尼系數，N·s/m。

引入階躍函數

式（16）在x、y方向的分量為

。

由其可得主銷與襯套間隙對主銷的碰撞力矩

。

式中，R為軸銷半徑，m。

2 主銷間隙對蛇行頻率特性影響的計算分析

以國產某型轎車為樣車，運用以上數學模型采用數值計算方法[18-19]對間隙影響樣車蛇行工況穩定性進行仿真分析，計算所需的樣車參數見表2。

2.1 間隙C對蛇行頻率特性影響

根據表2中樣車參數對其轉向梯形機構[圖1（c）]主銷間隙C分別取0，0.5，1，1.5，2，2.5，3 mm，取速度v為20 m/s，進行數值計算，尋找間隙對車輛蛇行工況頻率特性影響規律。蛇行工況下車輛質心側偏角頻率特性如圖3所示。并且對圖3（a）、（b）、（c）、（d）、（e）、（f）、（g）中取f=2.6 rad/s時相圖做相應的龐加萊映射和功率譜圖進行分析，結果如圖4所示。

圖3為不同主銷間隙（C=0，0.5，1，1.5，2，2.5，3 mm）時，車輛蛇行工況下，質心側偏角頻率特性分叉圖。表3為不同間隙車輛失穩時質心側偏角的上下臨界頻率及帶寬。間隙C取不同值時車輛蛇行工況一致性表現為由倍周期走向單周期，然后單周期走向混沌、倍周期，最后又回到單周期運動。但是不同間隙時，轉向蛇行工況質心側偏角隨轉向角頻率失穩的上下臨界頻率不同，且失穩頻率帶寬隨間隙增大而增大。由圖3及表3可見，當C=0～1.0 mm范圍時，分叉頻率帶寬較小，理論上說明在設計轉向節主銷與襯套間隙C<1.0 mm范圍有利于減小車輛蛇行失穩的幾率。

由此可見，隨著間隙C增加，汽車蛇行失穩的上臨界頻率幾乎無變化，而失穩的下臨界頻率逐漸加大，由其導致蛇形行駛失穩的頻率帶寬相應加大，說明轉向節主銷與襯套間隙過大，增加了車輛蛇行失穩的概率。但是通過以上數值計算，可以找到理論上減小車輛失穩的主銷與襯套間隙的較好區間（0，1.0） mm，能為設計與制造優選主銷間隙提供理論參考。

2.2 對圖3質心側偏角頻率特性的相圖分析

在圖3（a）、（b）、（c）、（d）、（e）、（f）、（g）分叉圖中有一個共同特點，樣車作蛇行行駛時，在f=2.6 rad/s處的分叉行為較復雜。因此對圖3統一取f=2.6 rad/s處做進一步細化，對質心側偏角的動力學行為作車輛蛇形頻率特性分析，車輛在該轉向頻率時，質心側偏角相圖、龐加萊映射及功率譜圖如圖4（a）、（b）、（c）、（d）、（e）、（f）、（g）所示。

圖4為圖3中f=2.6 rad/s時，的相圖、龐加萊圖及其功率譜圖。由圖4可見，當f=2.6 rad/s時，隨著間隙C增大，車輛質心側偏角分叉行為表現為由三倍周期走向混沌，但在C<1.0 mm時，系統周期解穩定性較好。主銷間隙C>1.0 mm后整車蛇形工況的動力學行為表現為混沌，車輛失穩行為表現得更加復雜。由此可能致使車輛在緊急工況下駕駛員急打方向盤而導致汽車甩尾、側翻事故。因此，為了安全，應及時檢查舊車轉向節主銷與襯套間隙是否超值，保證合理的安全間隙。對于產品設計，應該從車輛蛇行工況安全的角度合理選取轉向節主銷與襯套間隙。

3 結論

（1）考慮前輪主銷間隙建立了汽車轉向行駛四自由度系統動力學模型。

（2）通過對樣車前輪主銷間隙C取不同值時的數值計算，從質心側偏角頻率特性分叉圖及其相圖、龐加萊圖、功率譜圖發現，隨主銷間隙增加，整車系統一致性地表現為由倍周期進入單周期、混沌，然后從倍周期回到單周期。隨間隙C增加，車輛蛇行行駛失穩的上臨界頻率幾乎無變化，但失穩的下臨界頻率逐漸加大，失穩的帶寬相應加大，說明間隙C增加對車輛蛇形穩定性不利。理論上找到C<1.0 mm區間時車輛蛇行工況失穩區間較小，這一范圍在設計和制造上也易于實現。

（3）主銷間隙對車輛蛇行失穩的影響趨勢以及尋找到的有利于車輛蛇形穩定性的區間，能為車輛轉向橋設計提供理論參考。

參考文獻（References）：

Ren Yuanyuan，Zheng Xuelian，Li Xiansheng. Handling Stability of Tractor Semitrailer Based on Handling Diagram [J]. Discrete Dynamics in Nature and Society，2012，37（10）：1887-1991.

BLACK J，WAGNER J，ALEXANDER K，et al. Vehicle Road Runoff-Active Steering Control for Shoulder Induced Accidents[C]//American Control Conference，Seattle，WA，2008：3237-3244.

JONES I S. The Use of Accident Data in Studying Vehicle Handling Performance[C]//Proceedings of the Institution of Mechanical Engineers，1975：243-258.

CHUCHOLOWSKI C，V?GEL M，VON STRYK O，et al. Real Time Simulation and Online Control for Virtual Test Drives of Cars. High Performance Scientific and Engineering Computing [C]//Lecture Notes in Computational Science and Engineering，Springer，1999：1-10.

王軍年.電動輪獨立驅動汽車差動助力轉向技術研究 [D]. 長春：吉林大學， 2009.

Wang Junnian.Study on Differential Drive Assist Steering Technology for Electric Vehicle with Independent-Motorized-Wheel-Drive [D]. Changchun：Jilin University，2009.（in Chinese）

劉麗.車輛三自由度平面運動穩定性的非線性分析及控制策略評價 [D]. 長春：吉林大學，2010.

Liu Li. Nonlinear Analysis and Control Strategy Evaluation on the Stability of Vehicle 3-DOF Planar Motion[D]. Changchun：Jilin University， 2010.（in Chinese）

楊秀建.極限工況下周期轉向汽車側向動力穩定性及分岔分析 [J]. 公路交通科技， 2009， 26（11）：141-152.

Yang Xiujian. Analysison Lateral Dynamic Stability and Bifurcation of Vehicle Periodic Steering under Critical Condition [J]. Journal of Highway and Transportation Research and Development， 2009，26（11）：141-152.（in Chinese）

KIM J. Effect of Vehicle Model on the Estimation of Lateral Vehicle Dynamics [J]. International Journal of Automotive Technology，2010，11（3）：331-337.

肖懷陽. 四輪定位參數對蛇形工況下汽車頻率特性影響研究 [D].合肥：合肥工業大學， 2012.

Xiao Huaiyang. A Study on the Influence of Four Wheel Alignment Parameter at Frequency Characteristics on Vehicle Stability on Snake-Like Conditions [D]. Hefei：Hefei University of Technology， 2012.（in Chinese）

CHUNG T，YI K. Design and Evaluation of Side Slip Angle-Based Vehicle Stability Control Scheme on a Virtual Test Track [J]. Control Systems Technology，2006，14（2）：224-234.

余卓平，高曉杰，張立軍.用于車輛穩定性控制的直接橫擺力矩及車輪變滑移率聯合控制研究[J].汽車工程，2006，28（9）：844-848.

Yu Zhuoping，Gao Xiaojie，Zhang Lijun. A Study on Coordination of Direct Yaw Moment Control and Variable Wheel Slip Control for Vehicle Stability [J]. Automotive Engineering，2006，28（9）：844-848.（in Chinese）

NAGAI M， HIRANO Y，YAMANAKA S. Integrated Robust Control of Active Rear Wheel Steering and Direct Yaw Moment Control [J]. Vehicle System Dynamics： International Journal of Vehicle Mechanics and Mobility， 1997，27（5-6）：416-421.

郭孔輝.汽車操縱動力學 [M]. 長春：吉林科學技術出版社，1991.

Guo Konghui. Vehicle Handling Dynamics [M]. Changchun：Jilin Science and Technology Press，1991.（in Chinese）

魏道高，王子涵，張翼天，等. 轉向系間隙對操縱穩定性影響研究 [J].汽車工程，2014， 36（2）： 139-144.

Wei Daogao，Wang Zihan，Zhang Yitian. A Study on the Influence of the Clearance in Steering System on Vehicle Handling and Stability [J]. Automotive Engineering，2014，36（2）：139-144.（in Chinese）

唐錫寬，金德聞. 機械動力學 [M]. 北京：高等教育出版社，1983.

Tang Xikuan，Jin Dewen. Machine Dynamics [M]. Beijing：Higher Education Press，1983.（in Chinese）

靳春梅.含間隙機構非線性動態特性、控制及實驗研究[D].西安：西安交通大學，2001.

Jin Chunmei. Nonlinear Dynamic Behaviors and Control and Experimental Researches on the Mechanism with Clea-rance Connections[D]. Xi'an：Xi'an Jiaotong University，2001.（in Chinese）

PACEJKA H B. Tyre and Vehicle Dynamics（2nd Edtion）[M]. USA：SAE，2006.

劉延柱，陳立群. 非線性振動 [M]. 北京：高等教育出版社，2001.

Liu Yanzhu，Chen Liqun.Nonlinear Vibration [M]. Beijing：Higher Education Press，2001.（in Chinese）

KREUZER E. 非線性動力學系統的數值研究 [M].凌復華，譯. 上海：上海交通大學出版社， 1989.

KREUZER E. Numerical Investigation of Nonlinear Dy-namic System [M]. Ling Fuhua，Translate. Shanghai： Shanghai Jiaotong University Press，1989.（in Chinese）