動力柔化直板葉片動力學相似關系

趙曉宇，黃　海，曲　濤，郭　健，羅　忠

（1.中航工業集團沈陽發動機設計研究所，沈陽110042；2.空軍駐沈陽地區代表室，沈陽110031；2.東北大學　機械工程與自動化學院，沈陽110819）

動力柔化直板葉片動力學相似關系

趙曉宇1，黃海1，曲濤2，郭健3，羅忠3

（1.中航工業集團沈陽發動機設計研究所，沈陽110042；2.空軍駐沈陽地區代表室，沈陽110031；2.東北大學機械工程與自動化學院，沈陽110819）

針對考慮動力柔化效應的直葉片動力學相似模型設計的問題，提出一種考慮動力柔化效應的動力學相似模型設計方法。根據大范圍運動板的動力方程推導得到的矩形板動力平衡方程，結合直葉片運動特性，建立基于柔性體假設的直葉片動力平衡方程；運用相似原理，建立考慮動力柔化的旋轉柔性直葉片的動力學相似關系；通過分析所建立的相似關系，為了避免過高轉速引起試驗系統的高階振動，提出建立旋轉直葉片過渡試驗模型的方法，并分析其在直葉片剛性與柔性條件下的適用性；最后通過數值驗證相似關系的有效性和正確性。

振動與波；動力柔化；旋轉葉片；試驗模型；動力學相似；過渡模型

葉片是旋轉機械如航空發動機、壓縮機和汽輪機等大型旋轉機械裝備中的關鍵部件，由于其工作環境復雜，動力學問題很難用數學方法完全解決，必須通過物理試驗來研究。然而在工程實際中，直接采用原型實驗往往由于幾何尺寸、材料成本、實驗周期以及實驗難度等問題難以進行，因此通常考慮采用相似試驗模型進行實驗。

對葉片相似試驗模型的研究，國內外學者做了很多工作。郝燕平［1］對壓氣機葉片所涉及的幾個結構相似性問題進行理論研究，討論在保持氣動相似的條件下，模型葉片和原型葉片之間靜強度、振動特性、振動響應的相似性問題；羅忠［2］針對復合材料層合板類結構的相似模型設計問題，提出在固有特性相似條件下，畸變模型幾何尺寸區間的確定方法；陳小波［3］通過研究考慮旋轉葉片的離心剛化效應對葉片動力特性的影響，引入剛化系數，給出頻率修正公式；Friedmann［4］通過相似模型實驗與計算機仿真對比的方法，分析直升機旋轉葉片的氣動彈性特性等等。而對考慮葉片動力柔化效應的相似試驗模型研究文獻尚不多見。

葉片有剛性葉片和柔性葉片之分，剛性葉片作為剛體可不考慮旋轉時動力柔化效應，而柔性葉片作為柔性體工作時需考慮由轉速引起的變形效應影響，即動力柔化效應影響。對于高速旋轉葉片，其動力柔化效應對其動力特性影響不容忽視，柔化效應會增大葉片原有的自振頻率，嚴重時使得葉片不能正常工作。本文基于相似理論，建立考慮動力柔化效應的旋轉直葉片動力學相似關系，為葉片相似試驗模型研究提供一定理論補充。

1　動力平衡方程

矩形薄板的運動變形如圖1所示。圖中OXYZ為慣性參考系，其上建立非慣性參考系oxyz，板中面上的一點P0變形后為P，r、s分別為P點沿矩形板長度和寬度方向上的總伸長量，u1、u2、u3分別為x、y、z方向上的變形量。e1、e2、e3分別為x、y、z方向的單位向量。

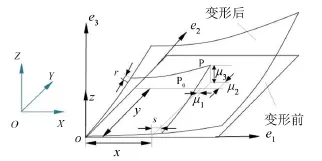
圖1　矩形薄板的運動變形圖

根據薄板變形理論［5］，由幾何應變位移關系可知

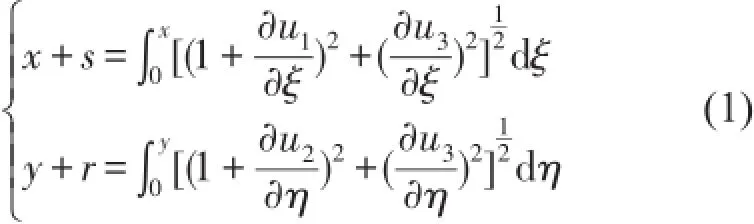
式（1）中，x、y為板上任一點坐標。

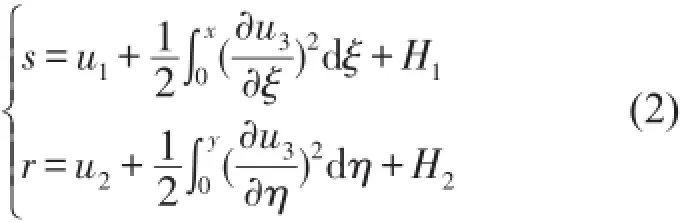
根據泰勒公式可將式（1）展開得式（2）中，H1、H2為高階小量。

忽略式（2）中高階小量，并將式（2）對時間t求導可得非慣性系統中x、y方向的速度為

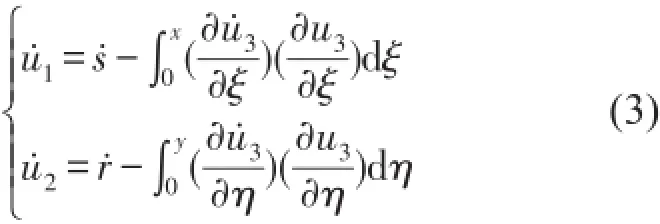
利用Rayleigh-Ritz法求解大范圍運動板的平衡方程，設

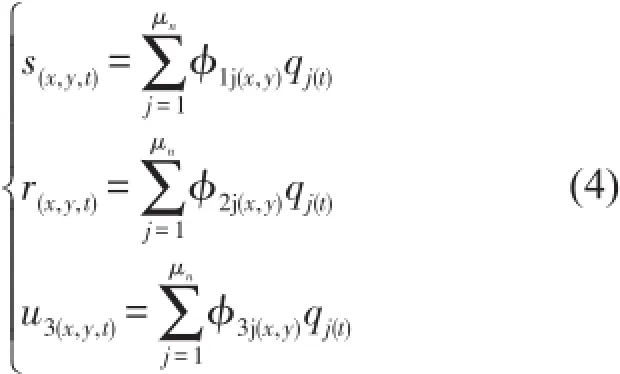
式（4）中，?1j（x，y）、?2j（x，y）為j階縱向振動振型函數，?3j（x，y）為j階橫向振動振型函數，qj（t）為廣義坐標，μn為總的振型函數個數。

矩形薄板的動力方程為［6，7］：

式（5）中，a、b、h分別為薄板的寬度、長度、厚度；ρ0為薄板單位面積質量；E為薄板材料彈性模量；μ為薄板材料泊松比；G為薄板的剪切模量，?i，x、?i，y分別為第i階振動振型函數對x和y的一階偏導；?i，xx、?i，xy、?i，yy分別為第i階振動振型函數對x、y的2階偏導；ω1、ω2、ω3分別為繞X、Y、Z軸旋轉的角速度；v1、v2、v3分別為薄板上點的速度。

聯立式（5）、（6）、（7）可求解位移函數s（x，y，t）、r（x，y，t）、u3（x，y，t）。

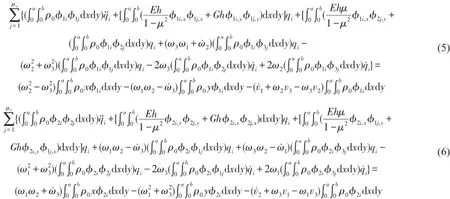
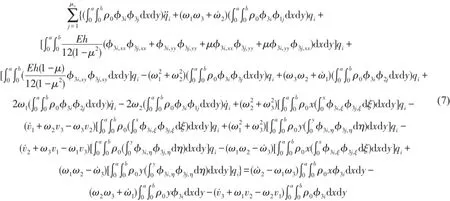
對如下圖2所示的懸臂矩形板模型的直葉片，R0為葉根半徑，葉片繞Y軸以角速度Ω轉動，其動力方程參數為將式（8）代入動力平衡方程可得直葉片的動力平衡方程為

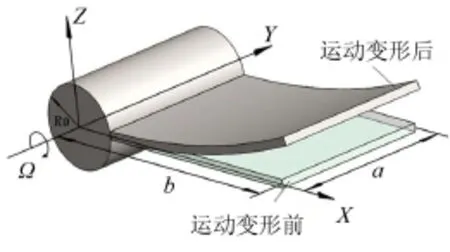
圖2　直葉片懸臂板模型

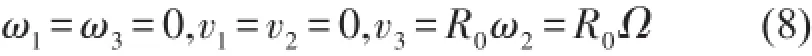
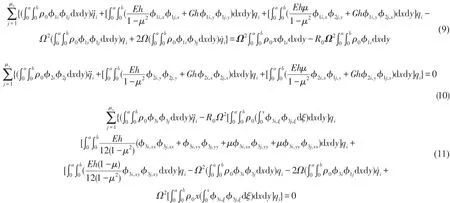
2　相似關系

設幾何相似關系為λ，λ為模型與原型的相似比，由相似原理知完全幾何相似時

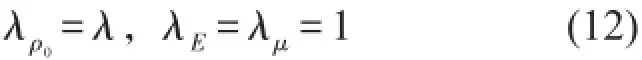
運用方程分析法，由式（9）、（10）、（11）可得相似關系式

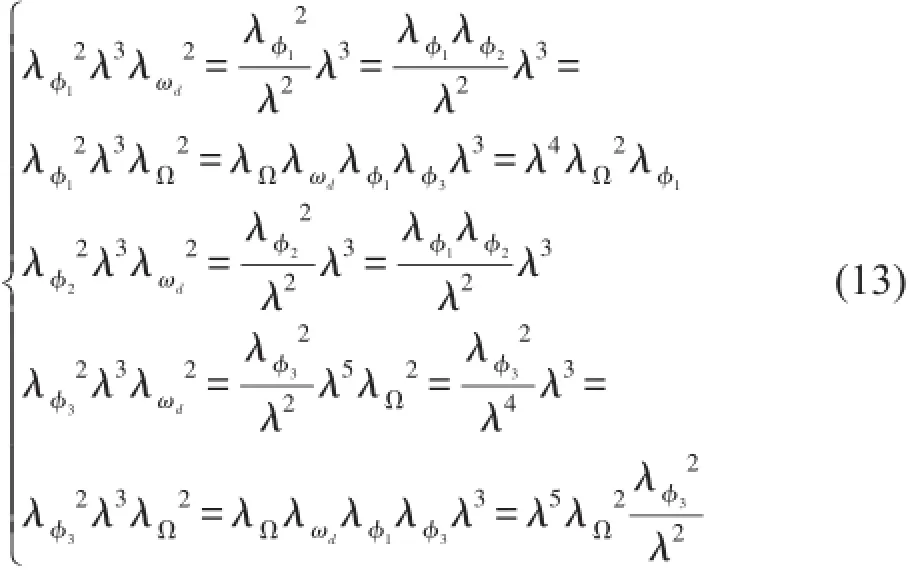
為橫向振型相似比；λΩ為轉速相似比；λωd為動頻率相似比。

由式（13）可知

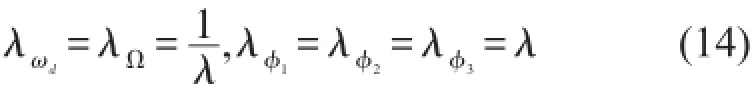
3　過渡模型

由式（14）知，轉速相似關系λΩ=1/λ，即模型葉片的轉速是原型葉片轉速倍，也就是模型越小，則要求轉速越高，而高轉速不僅會導致系統產生高階振動而影響測量結果，而且也使得實驗成本大大增加，故可考慮改變葉片動力相似模型中的轉速相似關系，通過建立低轉速的過渡相似模型來預測原型葉片的動力特性。

由葉片動頻率滿足［8］

式（15）中，ωd為動頻率；ω為靜態固有頻率；B為動頻系數；Ω為旋轉角速度。

建立過渡相似模型對原型動頻率進行預測，設過渡模型與原型相似關系為

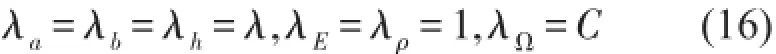
式（16）中，C為常數。

4　數值驗證

選用原型與模型直板葉片的幾何參數及轉速如表1所示［9-11］，取模型與原型材料參數相同，材料參數如下：彈性模量E=104.8 GPa，密度ρ=4 428 kg/m3，泊松比μ=0.3。設完全幾何相似相似比為λ=0.5。

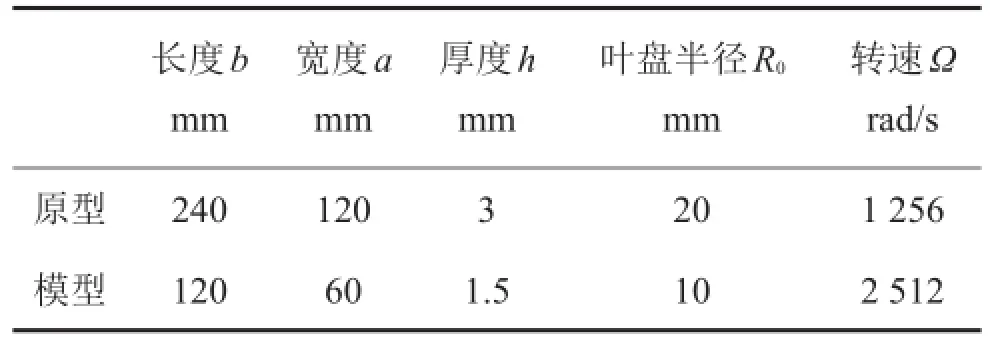
表1　原型和模型參數

采用實體單元分別對原型和模型直板葉片進行有限元建模，通過數值仿真計算得到考慮動力柔化效應的原型與模型前5階動頻率及通過相似關系式（14）由模型動頻率預測的原型動頻率如表2所示。

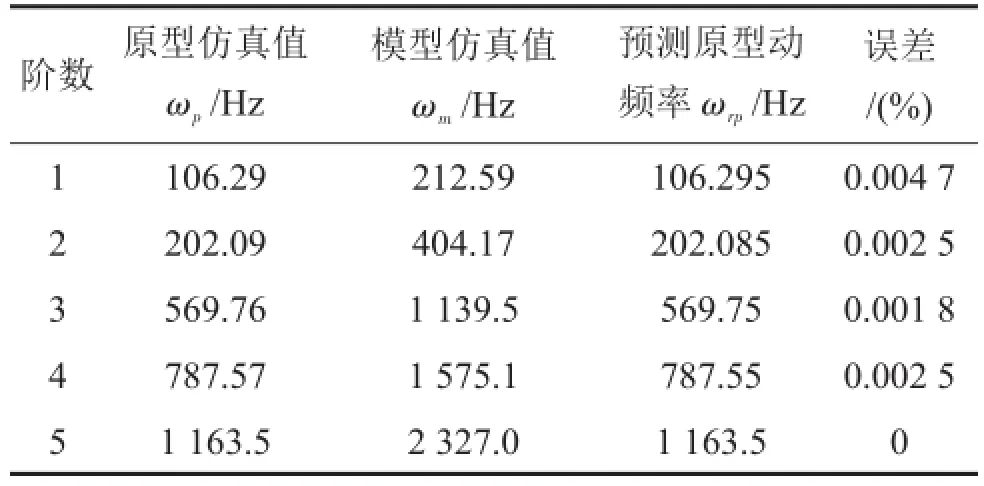
表2　原型和模型動頻率

由表2數值驗證結果可知式（14）所得相似關系是準確、可靠的。

對原型直板葉片施加n=0～1 256 rad/s的轉速（每隔157 rad/s為一個計算點），考慮動力柔化效應和不考慮動力柔化效應的各階動頻率如圖3所示。

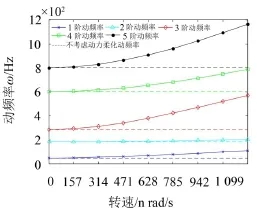
圖3　各階動頻率對比

由文獻［12］可知，建立過渡相似模型的可行性在于各階動頻系數B為常數，即動頻率對于旋轉角頻率為線性關系。對于柔性葉片，由圖3可知其動頻率隨轉速的變化為非線性關系，故不能通過過渡模型預測原型的動力特性。由此，對于剛性葉片的模型試驗，可通過過渡模型的方法在低轉速下對高速旋轉葉片進行模擬，而對于柔性葉片，試驗中則應保證其轉速的完全相似關系。

5　結語

運用相似原理，通過分析考慮動力柔化效應的直板葉片動力平衡方程，得到以下結論：

（1）考慮動力柔化的直板葉片動態固有頻率相似比與轉速相似比相同，是幾何尺寸相似比的倒數；

（2）數值仿真結果驗證了所建立相似關系是正確和有效的，并證明直板葉片的動力柔化效應對動頻率的影響隨轉速增大而增大；

（3）數值仿真結果驗證了對剛性葉片的模型試驗可通過建立較低轉速的過渡相似模型來避免試驗模型高階振動，對柔性葉片的模型試驗則應采用轉速完全相似的試驗模型。

［1］郝燕平.葉輪機葉片結構相似性問題的理論研究［A］.中國航空學會第六屆動力年會論文集［C］.南京，2006. CSAA06-P-084.

［2］羅忠，朱云鵬，陳曉兵，等.復合材料層合板相似模型的幾何區間確定方法［J］.機械工程學報，2014，50（9）：58-64. ［3］陳小波，李靜，陳健云.考慮離心剛化效應的旋轉風力機葉片動力特性分析［J］.地震工程與工程振動，2009，29 （1）：117-122.

［4］Friedmann P P.Aeroelastic scaling for rotary-wing aircraft with applications［J］.Journal of Fluids and Structures，2004，19（5）:635-650.

［5］YCFung.Foundationsofsolidmechanics［M］. Englewood Cliffs，NJ:Prentice-Hall，1965.

［6］Yoo H H，Chung J.Dynamics of rectangular plates undergoingprescribedoverallmotion［J］.Journalof Sound and Vibration，2001，239（1）:123-137.

［7］Yoo H H，Kim S K.Free vibration analysis of rotating cantilever plates［J］.AIAA Journal，2002，40（11）:2188-2196.

［8］沈慶樓，劉湘一，賈忠湖，等.發動機葉片振動特性分析［J］.海軍航空工程學院學報，2005，（04）：473-476.

［9］馬輝，能海強，宋溶澤，等.基于變厚度殼單元的旋轉葉片固有特性分析［J］.航空發動機，2013，39（5）：26-30.

［10］Qin Z Y，Yan S Z，Chu F L.Dynamic analysis of slender launching system connected by clamp band joint using harmonicbalancemethod［J］.JournalofPhysics: Conference Series，4 th Symposium on the Mechanics of Slender Structures，2013，448（1）:1-8.

［11］Qin Z Y，Yan S Z，Chu F L.Influence of clamp band joint on dynamic behavior of launching system in ascent flight ［J］.ProceedingsoftheInstitutionofMechanical Engineers，Part G:Journal of Aerospace Engineering，2014，228（1）:97-114.

［12］Yoo H H，Shin S H.Vibration analysis of rotating cantilever beams［J］.Journal of Sound and Vibration. 1998，212（5）:807-828.

Dynamic Similarity Relations of Straight Blades Considering Dynamic Softening Effects

ZHAO Xiao-yu1，HUANGHai1，QUTao2，GUOJian3，LUOZhong3
（1.AVIC ShenyangAero-engine Design Institute，Shenyang 110042，China；2.Air Force Representative Office of PLAin ShenyangArea，Shenyang 110031，China；3.School of Mechanical Engineering&Automation，Northeastern University，Shenyang 110819，China）

A method for dynamic similarity model design considering the dynamic softening effect was put forward. The dynamic equilibrium equations for rectangular plates were formulated based on the large displacement kinetic equations for moving plates.On this basis，combining with the kinetic characteristics of the straight blade，the dynamic equilibrium equation of the straight blade was established based on the flexural body assumption.Using the dynamic similarity principle，the dynamic similarity equation of the rotating straight blade was established.In order to avoid the high order vibration induced by over-high revolution speed，a method for establishing the transition model of the rotating straight blade was put forward.The applicability of the method was analyzed in the condition of rigid and flexible straight blades.Finally，the efficiency and correctness of the similarity relation were verified by numerical simulation.

vibration and wave；dynamic softening；rotating blade；experimental model；dynamical similarity；transition model

TH113.1

ADOI編碼：10.3969/j.issn.1006-1335.2015.05.008

1006-1355（2015）05-0043-05

2015－01－06

國家重點基礎研究發展計劃（973計劃）資助項目（2012CB026005）；教育部基本科研業務費專項資金資助項目（N130503001；N140301001）

趙曉宇（1980－），男，遼寧錦州市人，碩士，研究方向：整機動力學設計。

E-mail:rain65535@sina.com

羅忠（1978－）男，內蒙古集寧人，博士，主要研究方向：機械動力學與控制。

E-mail:zhluo@mail.neu.edu.cn