基于吉布斯耗散理論的生物量收率模擬計算

戚玉，孫巍

（北京化工大學化學工程學院，膜分離過程與技術北京市重點實驗室，北京 100029）

熱力學在化學中占有重要地位，它可以幫助人們判斷反應是否發生，以及在何種情況下發生。因而熱力學分析在化學、化工和化工工藝開發過程中都處于中心地位。

在生物工藝技術中，熱力學分析極少得到應 用[1]。人們都在期待，熱力學分析能夠預測一個給定的微生物生長過程或者新陳代謝反應是否可以發生，或者在什么條件下可以發生。基于熱力學分析，可以粗略地估計微生物培養技術的關鍵參數，因此，可以在實驗之前對微生物培養過程做經濟可行性分析。當第一步實施過后，熱力學分析結果將被當作參考基準，如果實驗結果遠不及計算結果，那么這揭示著在微生物培養過程中還有充足的空間可以提升[2]。在生物化工開發過程中，這些工作的意義不可估量。生物量收率是構成任何生物技術過程或者涉及微生物培養的實驗過程的一個關鍵參數[3]。因為它決定了最終生物量或者細胞濃度，必須強制進行優化，以得到合理的生產率。然而，對于不同的微生物生長系統，生物量收率變化范圍高達兩個數量級。國外一些研究人員已經試圖將一些生長過程變量（YAPT，Yave，吉布斯效率，焓效率等）用于預測生物量收率，但效果不是很理想[4]。

本文作者試圖證明可以從熱力學的角度來分析和預測生物量收率的變化。在基于von Stockar等的研究的基礎上，本文作者在基于吉布斯耗散理論構建的生物量收率模型的基礎上，嘗試著將生物熱力學應用到微生物生長和新陳代謝中，用碳源的一些參數，比如碳鏈長度及還原度等，作為估算吉布斯耗散函數的變量，探索吉布斯耗散函數和生物量收率之間的關系，以及其在實際應用中的深度及廣度。

1 吉布斯耗散函數

微生物在適宜的環境條件下，不斷地吸收營養物質，并按照自己的代謝方式進行代謝活動，如果同化作用大于異化作用，則細胞質的量不斷增加，體積得以加大，于是表現為生長。簡單地說，微生物生長就是微生物細胞組分與結構在量方面的增加，且細胞數目也有所增加[5]。同經典熱力學類似，在微生物生長過程中，也存在著驅動力。而吉布斯耗散函數則同生物量收率密切相關，首先對吉布斯耗散函數進行描述。

微生物生長過程是自發的，顯然這是一個高度不可逆過程，這必然伴隨著熵增。與生長反應相比較，這從表面上看來似乎是矛盾的。直觀地看，通過生長反應，一系列非常簡單的小分子合成了高度有序的物質，這一過程的熵是減少的[6]。

將一個生長的微生物細胞視作一個開放系統并進行熵平衡分析[7-8]，如圖1，物理量關系見式（1）。

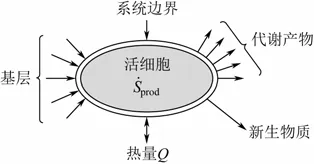
圖1 微生物細胞生長過程

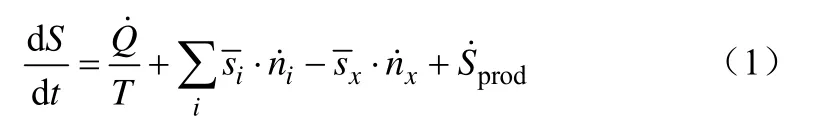
由于細胞內持續不斷的熵增prodS˙ ，并且不斷地有代謝物質進入細胞內，造成了熵在細胞內不斷積累，這就會導致細胞死亡或者細胞組織破壞瓦解。細胞可通過向環境排出多余的熵來避免上述局面，即使得為零，細胞生長得以維系[9]。

為了表示生化反應過程中的吉布斯能變GΔ ，可以將生化反應寫成宏觀反應方程。以化能營養型生長過程為例，生化反應式如式（2）。

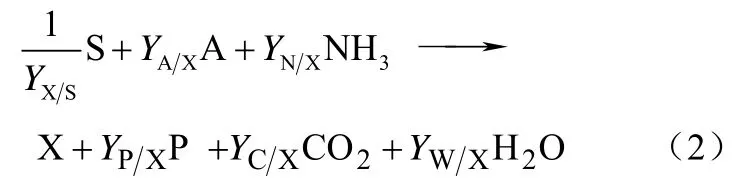
其中S、A、X和P分別表示碳源，電子受體或供體，新產生的生物量以及分解產生的廢棄物。YX/S表示基于碳源的生物量收率，Yi/X表示A、NH3、P、CO2和H2O相對于X的收率。所有的Y系數都可以視作生化反應的化學計量數。對于上述反應，假設細胞處于穩定態，得到式（3）。

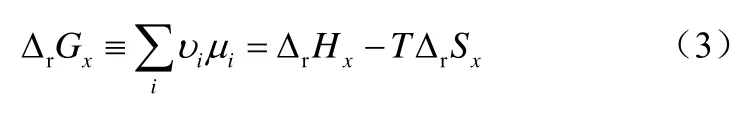
從式（3）可知，吉布斯耗散函數ΔrGx由焓和熵兩部分組成，這同微生物細胞同周圍環境進行的熱交換及代謝物質交換的情況是一致的，所以在構建吉布斯耗散函數及生物量收率之間的關系時，可以從焓和熵的角度進行考慮和分析。

2 吉布斯耗散函數和生物量收率之間的關系

2.1 熱力學模型

吉布斯耗散函數ΔrGx和生物量收率YX/S之間的關系可以通過將宏觀化學反應拆分成分解代謝反應和合成代謝反應來進行描述。合成代謝反應在合成生物質的同時產生了高吉布斯能的產物，因此相當于增加了生物反應器的吉布斯能。合成代謝反應因此受到同生長過程相反的驅動力，并且是消耗能量的。合成代謝反應所消耗的能量則是由耦合的分解代謝反應來提供。分解代謝反應帶來了巨大的吉布斯能耗以及釋放出大量能量。折合的凈吉布斯耗散函數ΔrGx顯然取決于合成代謝及分解代謝的化學計量數之間的數學關系，并且可以視作微生物生長過程的驅動力。而這種數學關系可以看作合成代謝過程強加于分解代謝過程之上的一種負荷，并可以通過生物量收率YX/S來表達。

在低效率的生長體系，合成代謝反應的負荷作用很小，消耗單位碳源和能量底物僅能產生少量生物量。生物量收率可能會很小，由合成代謝反應帶來的負荷幾乎沒有作用于分解代謝反應，這使得總的ΔrGx會是一個絕對值很大的負值。與之相對應的情況下，在高效率的生長體系中，這種負荷作用很大，并且會抵消分解代謝反應產生的ΔG，使得全過程ΔrGx是一個絕對值較小的負值。這種情況下，消耗單位底物所能產出的生物量就比較多，即生物量收率YX/S的值則會變大。極限條件下，假設這個負荷達到了一定數值，使得合成代謝反應及分解代謝反應達到平衡及ΔrGx等于零。這種情況可視作熱力學第二定律下的極限最高生物量收率YX/S；而熱力學平衡態下，反應速率無限慢。

在微生物生長系統中，可以預見，存在以下兩種極限情況：低負荷作用，大驅動力，新陳代謝劇烈，但很少的生物量及低的YX/S；低生長速率，最高的YX/S，生長過程無限慢。所以實際的微生物生長過程中，ΔrGx和YX/S是介于以上兩種極限情況之間的。

在實際生產過程中，水分、溫度、酸度、含氧量等環境因素都是要精確控制的，在本文討論的過程中，對以上環境因素都做了假設處理，假設以上因素都控制在微生物生長的最適條件下。例如，在淀粉質原料發酵酒精時，最適溫度為30～32℃，最適合pH值為4.8～5，并且在好氧代謝情況下，可獲得較高的細胞產量[10-11]。

為了從數學表達式上表示出吉布斯耗散函數ΔrGx和生物量收率YX/S的關系，可以把宏觀反應方程劃分成分解代謝和合成代謝兩個部分，如式（4）、式（5）。

分解代謝部分

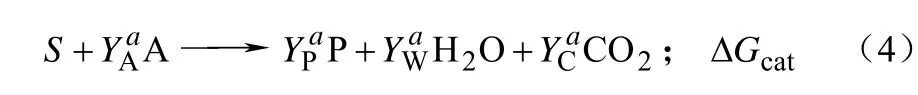
合成代謝部分

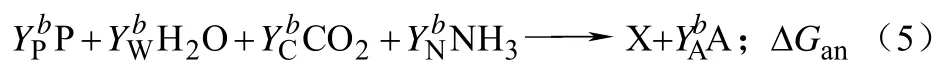
按照這種劃分方式，假定碳源S首先完全被分解代謝，之后分解代謝的產物才被用于生物量的合成代謝過程。雖然這種假定是不符合實際的，但是在這種假設情況下，卻可以得到簡單的化學計量關系；而有了這些簡單的計量關系，通過確定分解代謝反應，可以估算得到分解代謝反應的ΔG。而合成代謝反應由于其過程的高度復雜性，所以其實際反應的化學計量數不可估量。盡管對合成代謝反應進行了高度簡化，只要將以上倆式合起來使用，那么計算結果就比較準確。

通過式（4）、式（5），可以得到ΔrGx和YX/S之間的定量數學關系，如式（6）。

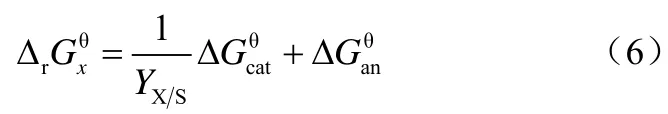
由于生命系統是遠離平衡狀態的，濃度修正項就顯得不是那么重要，所以可以使用標準吉布斯焓來參與計算。

2.2 微生物生長數據分析

下面從幾個不同生長過程來說明吉布斯耗散函數和生物量收率之間的關系。

圖2表示了吉布斯耗散函數和生物量收率之間的關系，使用的是葡萄糖基質上的耗氧生長實驗數據[12]。實心符號是數據，實心符號是數 據。和YX/S數據通過生物反應量熱計測得；數據由生化反應中物質的燃燒焓計算得來，下同。粗線是根據式（6）得到的吉布斯耗散函數和生物量收率YX/S的函數關系；相應的細線則是隨著生物量收率YX/S的函數關系。這兩條線如此接近表明，接近于零，即葡萄糖基質上的耗氧生長過程幾乎就是焓驅動的，不可逆過程產生的熵基本上是以熱的形式輸出到外界環境中的。

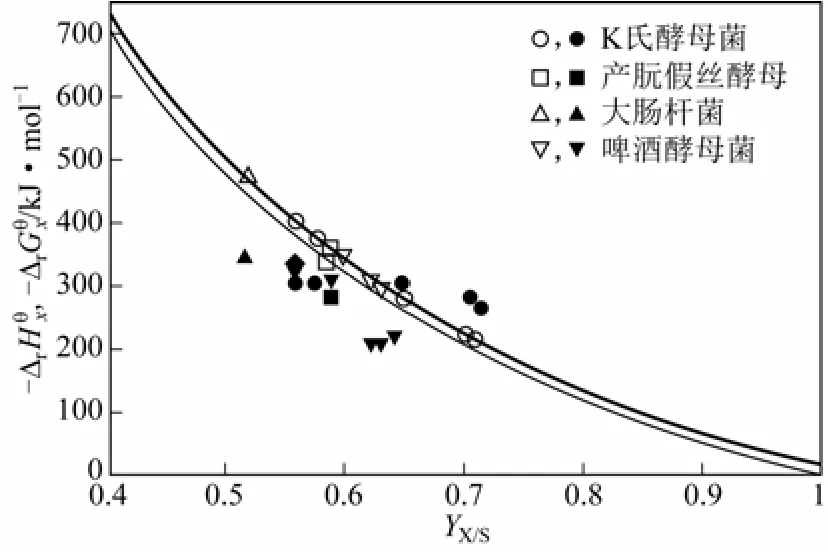
圖2 葡萄糖基質上的有氧呼吸

由圖2可見，對于不同菌種，不同生長條件及速率，生物量收率和反應焓變化范圍很窄；雖然生物量收率較大，但和最大理論收率還是有很大差距。這同上文中提到的兩種極端情況是一致的。吉布斯耗散函數大致由-250kJ/mol變化 到-500kJ/mol，測得的大致也在這個范圍內 變化。

圖3同圖2類似，以馬克斯克魯維酵母和啤酒酵母菌的厭氧發酵為例[14]。實心符號是空心符號是數據。分解代謝反應產生了乙醇，反應方程如式（7）。

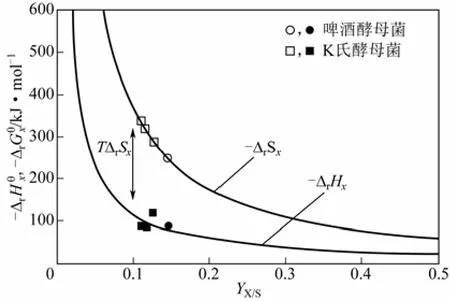
圖3 葡萄糖基質上的厭氧發酵[13]

對比圖2、圖3可以看出，葡萄糖培養基上的吉布斯耗散函數的數量級沒發生變化，但是在厭氧生長過程中，生物量收率較耗氧生長過程來說較低。由圖中數據可以說明，為了維持生長所需吉布斯耗散函數，而造成了這種較低的生物量收率。

巴氏甲烷八疊球菌，是一種產甲烷菌，它可以進行代謝反應并釋放甲烷[15]，反應式如式（8）。

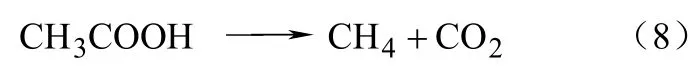
在這個過程中，產出的物質甲烷和二氧化碳的化學能比原料乙酸的化學能高得多，這就需要從環境中吸收熱量來補充原料和產物之間的能量差值。同樣的，的數值依然沒有發生太大波動，在-500 kJ/mol左右。

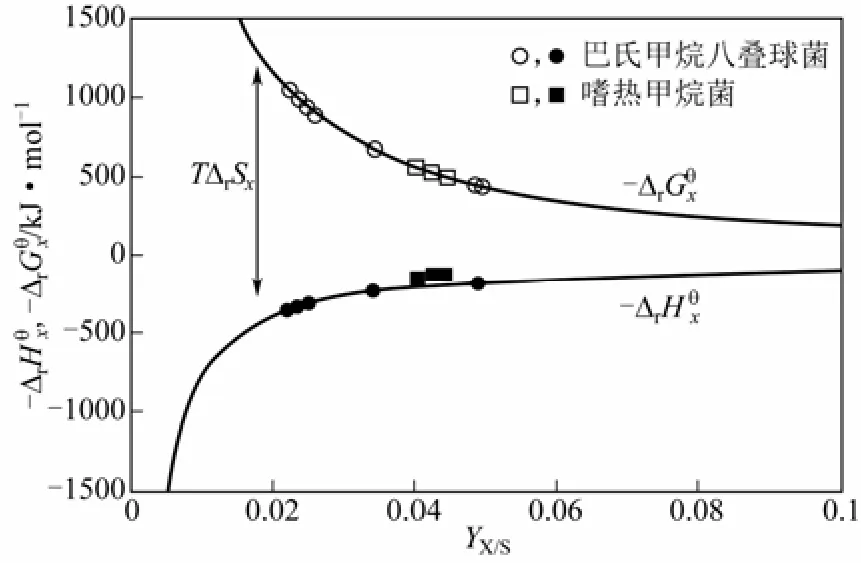
圖4 甲烷菌產甲烷過程[13]

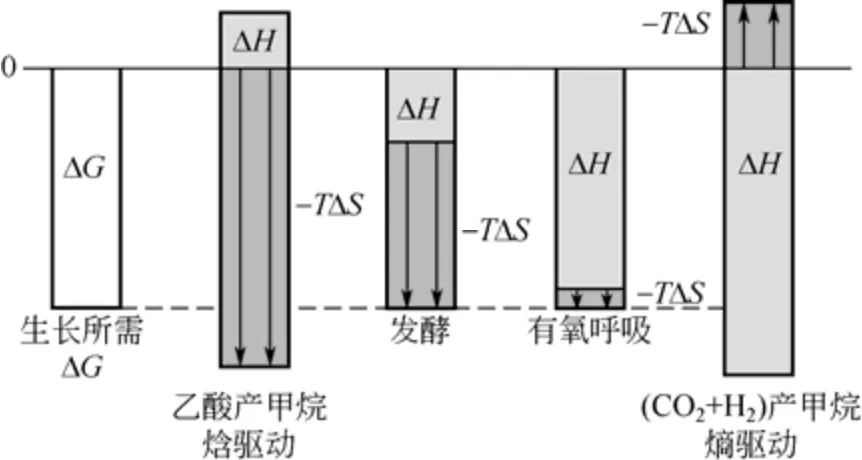
圖5 焓驅動和熵驅動生長過程[13]

3 生物量收率預測

基于上文內容，將式（6）變化得到生物量收率表達式，如式（9）。

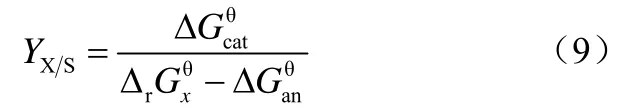
由這個式子就能計算并預測YX/S。首先可以從反應方程式（4）和式（5）來估算及，這就要求方程中的組分S、A、P已經準確定義，且化學計量數已經確定或者可以從已知條件中估算。以方程式（4）和式（5）為例，在組分A、P確定的情況下，方程中的未知數分別剩余3到4個，通過電子守恒及碳氧氮元素守恒即可求得。方程參數求得即可通過計算得到和數據，此處不再贅述。 當和 數據得出時，關鍵參數吉布斯耗散函數 Δ的估算至關重要。通過已經公開發表的數據分析，對于有氧呼吸生長過程來說，吉布斯耗散函數與電子受體A本身無關，和碳源的碳原子個數C及生化反應過程中的還原度γs有關。通過數據回歸得到回歸經驗關聯式如式（1）。

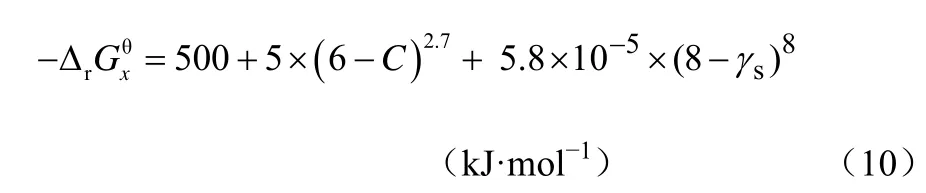
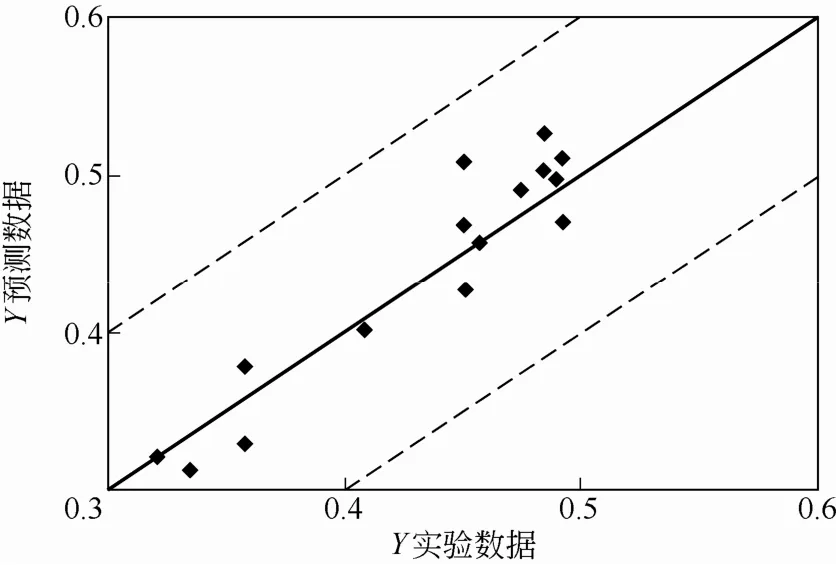
圖6 預測數據和實驗數據

圖6中上下兩條線表示±0.1偏差線，可以見到預測數據的誤差大致在11%以內。這是由于在構建預測模型時只考慮了碳源的碳原子個數C及生化反應過程中的還原度γs兩個參數，模型的構建還需要考慮更多參數。

4 結 論

符 號 說 明

[1] Angenent L T，Karim K，Al-Dahhan M H，et al. Production of bioenergy and biochemicals from industrial and agricultural wastewater[J].Trends in Biotechnology，2004，22（9）：477-485.

[2] Zainetdinov R I. Dynamics of informational entropy associated with self-organisation process in open system[J].Chaos，Solitons & Fractals，1999，10（9）：1425-1435.

[3] Molinuevo-Salces B，Larsen S U，Ahring B K，et al. Biogas production from catch crops：Evaluation of biomass yield and methane potential of catch crops in organic crop rotations[J].Biomass and Bioenergy，2013，59：285-292.

[4] Heijnen J J，Van Dijken J P. In search of a thermodynamic description of biomass yields for the chemotrophic growth of microorganisms[J].Biotechnology and Bioengineering，1992，39（8）：833-858.

[5] Lucia U. Thermodynamic paths and stochastic order in open systems[J].Physica A：Statistical Mechanics and its Applications，2013，392（18）：3912-3919.

[6] Marín D，Martín M，Sabater B. Entropy decrease associated to solute compartmentalization in the cell[J].Biosystems，2009，98（1）：31-36.

[7] Yu M B. Influence of environment and entropy production of a nonequilibrium open system[J].Physics Letters A，2008，372（15）：2572-2577.

[8] 蔣愛華，梅熾，時章明. 泛火用分析方法及其應用[J]. 中南大學學報：自然科學版，2011，42（2）：528.

[9] Lucia U. Irreversibility in biophysical and biochemical engineering[J].Physica A：Statistical Mechanics and its Applications，2012，391（23）：5997-6007.

[10] 岳國君. 現代酒精工藝學[M]. 北京：化學工業出版社，2011.

[11] 程坷偉，許時嬰，王璋. 采用無機陶瓷膜超濾甘薯淀粉生產廢液中的糖蛋白的工藝研究[J]. 食品與發酵工業，2005，30（12）：88-91.

[12] Somashekar D，Venkateshwaran G，Sambaiah K，et al. Effect of culture conditions on lipid and gamma-linolenic acid production by mucoraceous fungi[J].Process Biochemistry，2003，38（12）：1719-1724.

[13] Von Stockar U，Liu J S. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth[J].Biochimica et Biophysica Acta：(BBA)-Bioenergetics，1999，1412（3）：191-211.

[14] Liu J S，Marison I W，Von Stockar U. Anaerobic calorimetry of the growth of Lactobacillus helveticus using a highly sensitive Bio-RCl[J].Journal of Thermal Analysis and Calorimetry，1999，56（3）：1191-1195.

[15] 佘晨興，仝川. 自然濕地土壤產甲烷菌和甲烷氧化菌多樣性的分子檢測[J]. 生態學報，2011，31（14）：4126-4135.

[16] Annila A，Salthe S. Physical foundations of evolutionary theory[J].Journal of Non-Equilibrium Thermodynamics，2010，35（3）：301-321.