T-S 模糊系統量化H∞濾波器設計
趙 迪, 常曉恒
(1. 渤海大學 數理學院, 遼寧 錦州 121003; 2. 渤海大學 工學院, 遼寧 錦州 121003)
自1985 年Takagi 和Sugeno[1]提出了著名的T-S 模糊系統模型來描述復雜的非線性系統以來,T-S 模糊模型作為處理非線性系統的有效手段吸引了眾多學者的關注[1-4]。 針對T-S 模糊系統的研究主要從T-S 模糊系統的穩定性分析和控制器、濾波器的設計兩方面展開。 而狀態估計作為控制領域的一個基本問題,模糊系統的狀態估計也得到了廣泛的研究,尤其是基于H∞濾波理論的T-S 模糊系統狀態估計[2-4]。另一方面,伴隨著數控時代的到來和網絡化控制的興起,反饋控制系統中存在的量化現象作為一個不可回避的問題也受到了廣泛的關注[8-10]。 這是因為在傳統的控制器、濾波器的沒有考慮量化的影響,而量化現象又是普遍存在的,這就導致了當系統量化發生時,系統性能下降甚至不穩定。 其實有關于量化問題的研究最早可以追溯的1956 年,卡爾曼[8]指出了一個可穩定的量化控制器可能導致閉環系統出現極限環和混沌現象。 基于此,許多學者展開了對量化問題的研究從最早的理解和克服量化的影響到現在把量化器看作是信息編碼器,提出了許多重要的成果[9-10]。
本文考慮了存在量化現象的離散T-S 模糊系統的狀態估計問題, 主要是基于H∞濾波理論給出一套比現有方法保守性更低可行的濾波器設計算法使得T-S 模糊系統存在量化時達到漸進穩定并滿足給定的H∞性能指標。
1 問題描述
考慮以下離散T-S 模糊模型,其第i 條模糊規則為
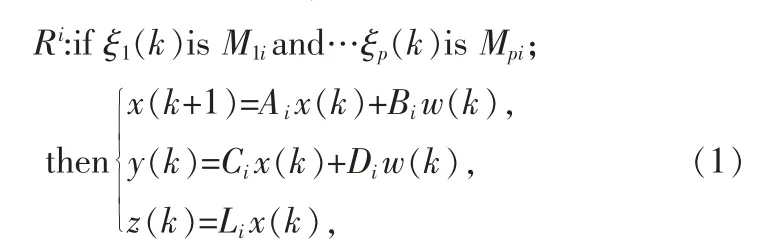
其中x(k)∈Rn為狀態變量;y(k)∈Rf為測量輸出信號;z(k)∈Rq為被估計信號;w(k)∈Rv為噪聲信號且能量有界即w(k)∈l2(0,∞),ξ1(k),ξ2(k),…ξp(k)為可測量的前提變量,Mdi,d=1,2,…p,i=1,2,…r 是模糊集,r 為模糊規則數目,Ai,Bi,Ci,Di,Li為適當維數的系統矩陣。是前提變量ξd(k)相對于模糊集合Mdi的隸屬度且滿足
T-S 模糊模型(1)可寫為如下形式:
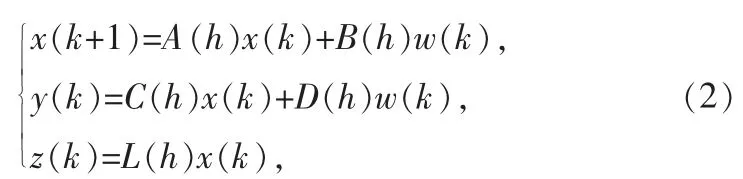
其中Λ(h)=hi(ξ(k))Λi,Λ=A,B,C,D,L。
考慮如下形式的全階模糊濾波器:
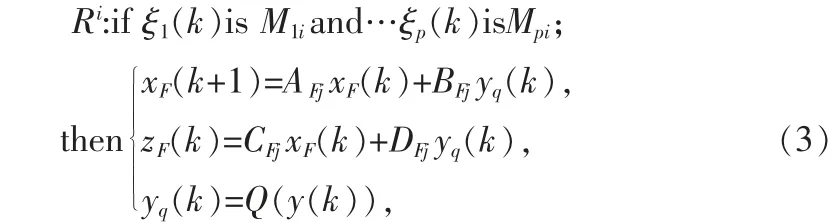
其中xF(k)∈Rn,yq(k)∈Rf,zF(k)∈Rq分別是濾波器的狀態、輸入和輸出,AFj,BFj,CFj,DFj,j=1,2,…r 為需要設計的適當維數的矩陣。其中函數Q(·)表示對數量化器。本文考慮采用靜態時不變對數量化器。 即Q(·)=[Q1(·),Q2(·)…Qf(·)]T并且滿足Q(-V)=-Q(V)。根據Fu 等人定義[13],對于(3),可以得到對于任意y(k)∈Rf有|Q(y(k))-y(k)|≤δy(k),δ=diag(δ1,δ2,…,δf)。 因此,yq(k)=Q(y(k))=(I+Δ(k))y(k),|Δ(k)|=diag(Δ1(k),Δ2(k),…,Δf(k))。 量化現象時,對于系統(2),其輸出信號y(k)傳送到濾波器時應變為Q(y(k))。
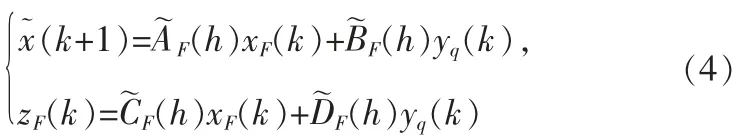
至此我們的目的可以闡述為針對上述存在輸出量化現象T-S 模糊系統,設計濾波器(3)使系統在消除量化誤差的影響同時,滿足R1)和R2)。
R1)當w(k)=0 時,濾波誤差系統(4)穩定。
R2)在零初始條件下即x~(k)=0,對于任意w(k)∈l2(0,∞),濾波誤差系統(4)都能夠滿足給定的H∞噪聲裕度γ,即‖e(k)‖2<γ‖w(k)‖2。
下面的引理在后續研究中起關鍵作用。
引理1[6].給定矩陣Θ=ΘT∈Rn×n,和N∈Rn×n,不等式vTΘv<0,?v∈Rn,Nv=0,v≠0 成立,如果存在矩陣L∈Rn×n,滿足Θ+LN+NTLT<0。
引理2[5].給定矩陣Γ,Λ,和對稱矩陣Ω,對于FTF≤I,不等式Ω+εΓFΛ+ΛTFTΓ<0 成立, 只要存在一個恒定的標量ε>0,滿足Ω+ε-1ΓΓT+εΛTΛ<0。
2 系統H∞性能分析
定理1:濾波誤差系統(4)在滿足給定的H∞指標γ 的前提下穩定,如果存在矩陣P+(h)>0,P(h)>0,N(h),M(h),X1(h),X2(h),X3(h),E,F,G 滿足下面的矩陣不等式:
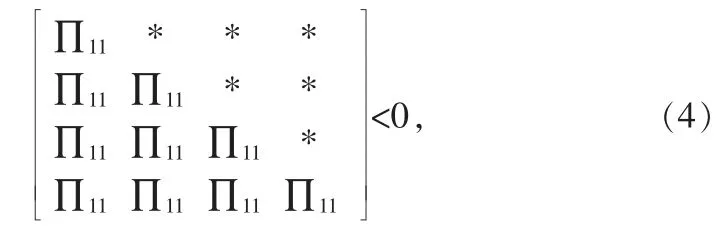
其中,
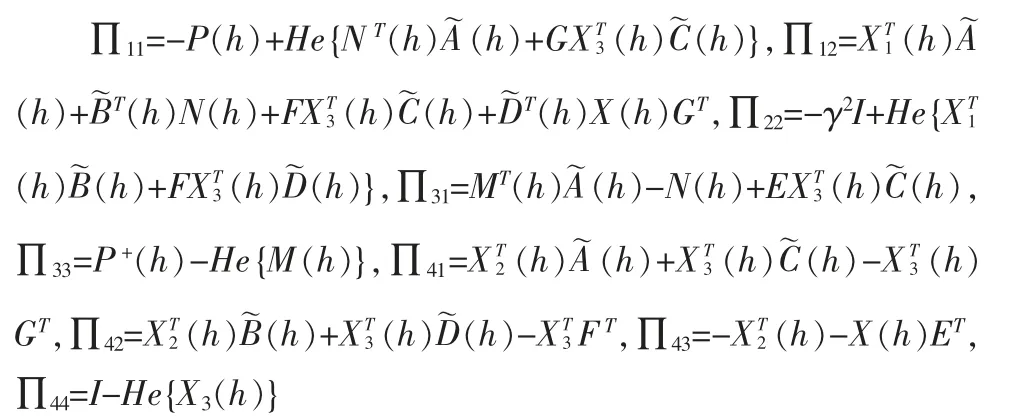
證明:構造如下模糊Lyapunov 函數:
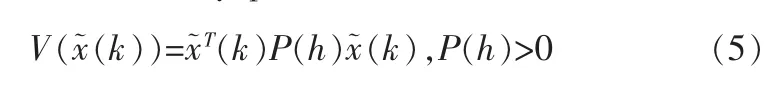
其差分為
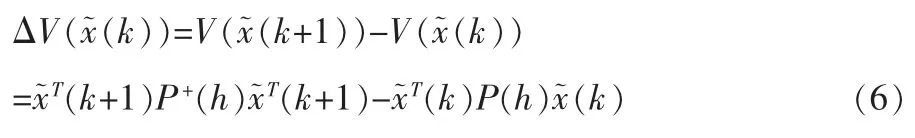
進而可得
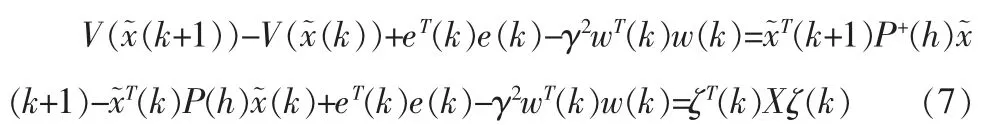
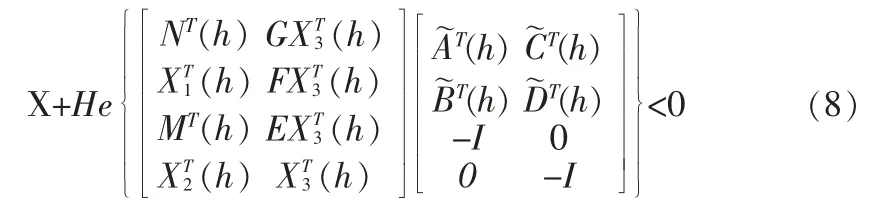
注1:我們推廣Chang[4]中的方法來處理T-S 模糊系統H∞量化濾波問題,注意到當定理1 中E(h)=F(h)=G(h)=0 時,定理1 的結論降級為推廣Chang[4]中所得的結果,由此可得對于T-S 模糊系統量化H∞濾波問題定理1 的設計條件比Chang[4]中的方法理論上保守性更低。 定理1 沒有考慮量化誤差的影響。 接下來,我們將給出充分條件來消除量化誤差的影響。
定理2:假設系統和濾波器已給出,則濾波誤差系統(3)在滿足H∞范數指標γ 的情況下達到一致穩定當且僅當存在P+(h)>0,P(h)>0,N(h),M(h),X1(h),X2(h),X3(h),E,F,G 以及標量ε>0 滿足下面的矩陣不等式:

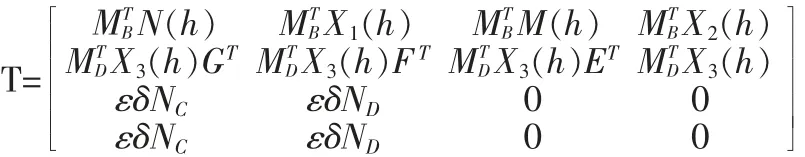
并且Φij為(4)中的∏ij用代替(4)中的所得。
證明:假設定理1 中的條件是滿足的。 我們把(3)中的定義帶入定理1 的結論,則(4)可寫為如下形式:
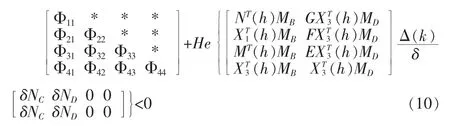
其中,MB=[0,MD=-DF(h),[C(h),0],ND=-D(h)則對(10)應用引理2 可得(10)成立當且僅當存在一個標量ε>0,滿足:
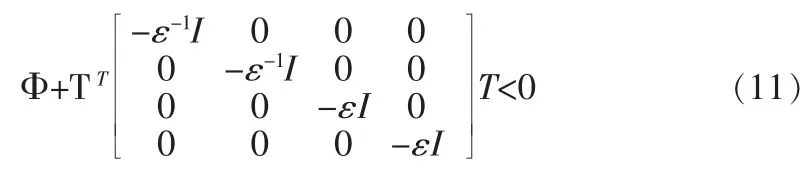
對(11)應 用Schur 補,最 后 再 調 用diag(I,I,I,I,I,I,εI,εI)執行同余變化,則可得定理2 的結論。
基于定理2,我們將給出線性化過程來設計H∞濾波器。
3 H∞濾波器設計
定理3:給定量化密度ρ>0,對于離散T-S 模糊系統,存在濾波器能夠消除量化誤差并且能夠保證濾波誤差系統在滿足給定H∞裕度γ 的前提下漸進穩定的條件是,存在矩陣P1i,P2i,P3i,P1l,P2l,P3l,N1j,N2j,M1j,M2j,X1j,X2j,i,j,l=1,2,…,r,G,E,F 和非奇異矩陣N3,X 以及標量λ1,λ2,λ3,λ4,λ5,ε>0 滿足下面的線性矩陣不等式:

對于i,j,l∈(1,r),其中
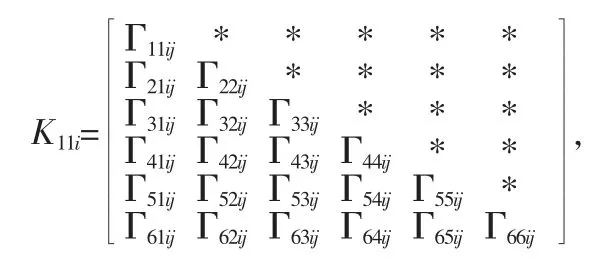
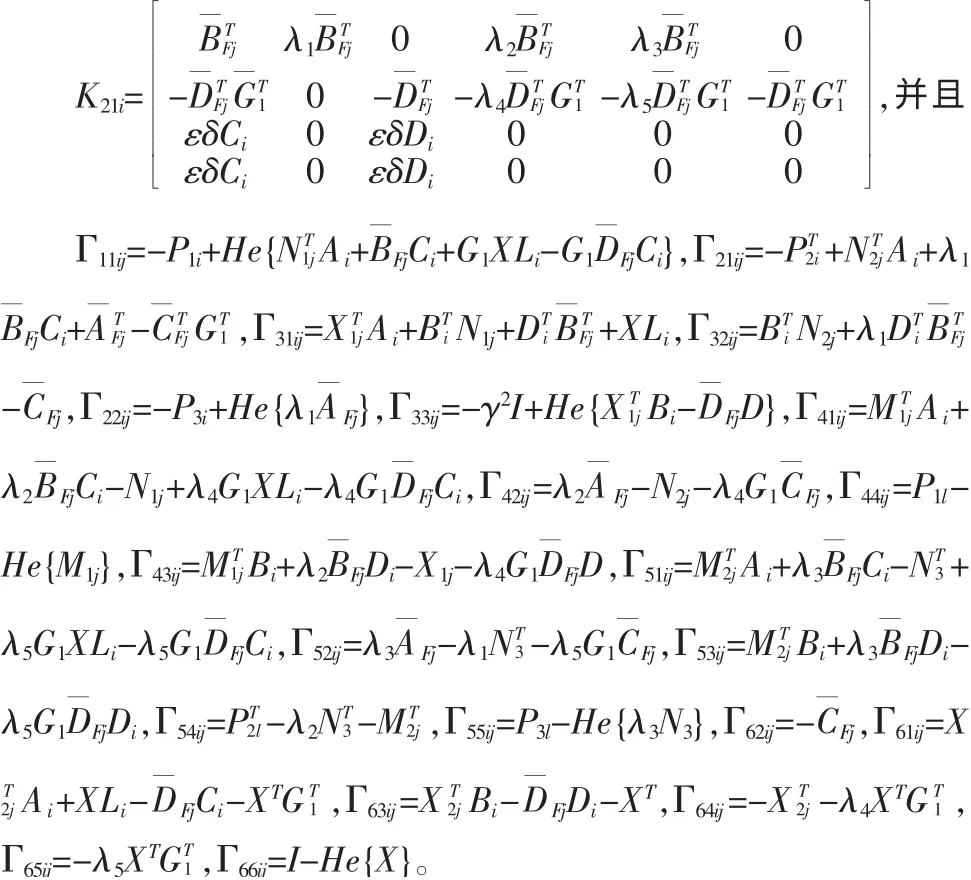
由此, 可以得到一個滿足給定H∞性能指標γ>0 的合適濾波器:
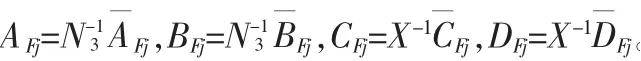
證明:如果定理2 中不等式成立,我們便可以設計濾波器,這里假設在(9)中涉及到的矩陣變量具有如下的形式并且定義:,
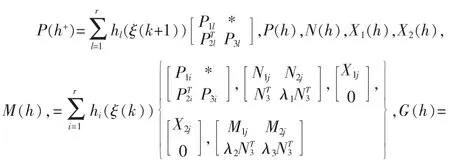
注2: 通過對定理2 上面的相關矩陣做上述結構上的定義, 可以使得原先在定理2 的不等式中出現的那些耦合項很好的分開了。另一方面,為了降低這樣對矩陣變量結構上定義帶來的保守性, 文中引入了幾個補償參變量λl,l=1,2,3,4,4和G1來獲得解空間中額外的自由度。 這些變量可以利用Chang[7]中提到的方法得到。
注3:在實際的應用中,量化誤差的上限δ 可以根據給定的量化密度ρ 計算得到。 因此, 定理3 中的不等式組 (12)-(13) 實際上是嚴格的線性矩陣不等式 (LMIs), 故可以通過MATLAB 的控制工具箱來求解從而設計濾波器。
4 仿真分析
本節我們將通過實例驗證之前論述的方法的有效性。 考慮隧道二極管電路,其T-S 模糊模型如[5,7]所描述其中,
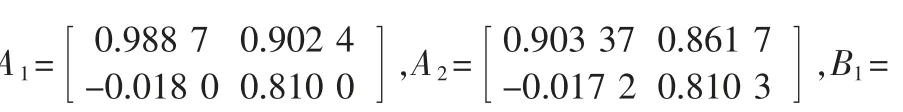
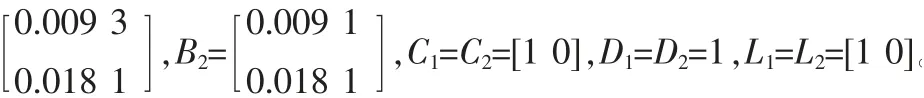
我們給定(13)中的優化參數如下λl=-0.15,l=1,2,3,λl=我們用定理3 中的方法來處理T-S 模糊系統H∞量化濾波問題,得到相應的γmin為1.3408。 對應定理3求得的濾波器參數矩陣如下:
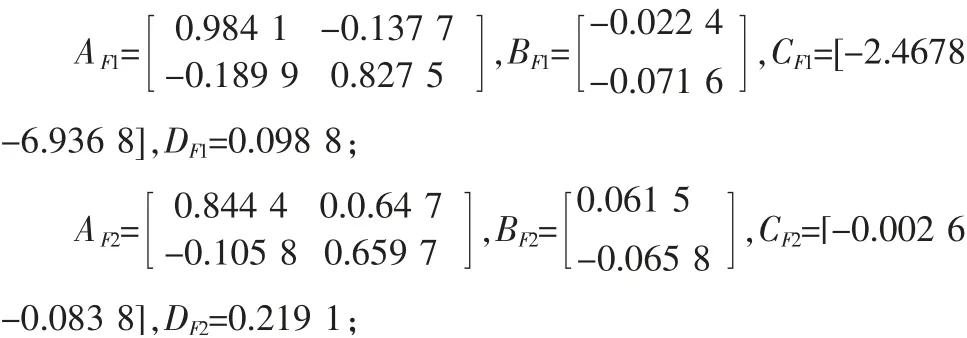
5 結 論
文中解決了離散T-S 模糊系統的量化濾波問題, 采用模糊Lyapunov 函數方法和松弛變量的引進,給出了基于LMI 技術一種量化H∞濾波器設計的充分條件。理論證明顯示了所提方法的優越性,最后通過仿真實例驗證該方法的有效性。
[1] Takagi T,Sugeno M. Fuzzy identification of systems and its applications to modeling and control [J]. Systems, Man and Cybernetics, IEEE Transactions on,1985(1):116-132.
[2] Gao H,Zhao Y,Lam J,et al. Fuzzy filtering of nonlinear systems with intermittent measurements[J]. Fuzzy Systems,IEEE Transactions on,2009,17(2):291-300.
[3] Zhou S,Lam J,Xue A. H∞filtering of discrete-time fuzzy systems via basis-dependent lyapunov function approach[J].Fuzzy Sets and Systems,2007,158(2):180-193.
[4] Chang X H,Yang G H. Non-fragile H∞filter design for discrete-time fuzzy systems with multiplicative gain variations[J].Information Sciences,2014,266:171-185.
[5] Petersen I R. A stabilization algorithm for a class of uncertain linear system[J]. Systems & Control Letters,1997,8(4):351-357.
[6] Skelton R E,Iwasaki T,Grigoriadis K. A unified approach to linear control design[M]. CRC Press,1997.
[7] Chang X,Yang G. Robust H-infinity filtering for uncertain discrete-time systems using parameter-de pendent Lyapunov functions [J]. Journal of Control Theory and Applications,2013,11(1):122-127.
[8] Kalman R E. Nonlinear aspects of sampled-data control systems[C]//Proc. Symp. Nonlinear Circuit Analysis VI. 1956:273-313.
[9] Fu M,Xie L. The sector bound approach to quantized feedback control [J]. Automatic Control, IEEE Transactions on,2005,50(11):1698-1711.
[10]Gao H,Chen T. A new approach to quantized feedback control systems[J]. Automatica,2008,44(2):534-542.

