高中數學課堂情境創設的點滴體會

戴興達

摘 ? ?要： 在高中數學課堂教學中，教師根據教學內容靈活地進行情境創設，以更好地激發學生的學習興趣，培養學生的數學能力，提高學生的數學素養。

關鍵詞： 高中數學課堂教學 ? ?情境創設 ? ?教學內容

在大多數學生眼里，數學學科抽象枯燥，且對于現實的生產生活沒什么用處，在實際生活中只要懂得一些基本的計算就可以了，也就是只要小學畢業就可以了，至于高大上的中學數學和大學數學是科學家的事情，我們不當科學家，所以沒必要學得太精。很多高中生特別是文科生，已經做好了一上大學便徹底告別數學的準備，所以在中學學習數學只不過是為了應付考試。因此，如何在課堂上充分調動學生的學習積極性，讓學生領略到數學的魅力，發現生活生產中無處不在的數學，進而對數學產生興趣，已成為數學教師的首要任務。

現代教育提倡的是素質教育，不應只注重傳授課本知識，更應培養學生的數學能力，提高學生的數學素養。所以，在教學中教師應該充分發揮學生的主體作用，讓學生在學習中積極主動地思考，使學生經歷從發現到懷疑，到思索，再到新的發現，最后解惑的奇妙過程體驗，讓學生自覺地用數學思維解決問題。由于青少年在接受新知識時往往是先從感官開始的，這就需要教師通過課堂的精心設計刺激學生的感觀認識，把抽象的數學知識形象化、直觀化、具體化，讓學生經歷數學概念和公式的產生過程，進而激發學生學習數學的興趣，因此課堂上情境的創設顯得尤為重要。

1.借用數學史和數學家的故事創設情境，吸引學生的注意力

課堂教學是一種創造性的勞動，不同的老師創造出不同的課堂、不同的教學方法，從而達到不同的教學效果。所以在教學中激發學生的好奇心，調動學生的學習興趣至關重要。因此課堂教學要非常重視新課引入，一堂好課必定要有一個好的開頭，也才會引起學生的注意，而介紹數學史和數學家的故事就是一個好的方法。

比如，我們在介紹集合知識時，可適當介紹康托集合論的成就;在講授“直線與圓的位置關系”時就可以借助選修系列3-1《數學史選講》第三章，簡要介紹解析幾何的誕生;在講授微積分知識之前，可介紹中國古代的“一尺之棰，日取其半”的論斷，此論斷蘊含無窮小的思想;祖沖之的求π“割圓術”，這是極限思想的原始模型;祖暅的“等冪等積定理”等。通過數學史的簡要介紹，讓學生體會數學其實源于生活用于生活，體會古代科學家的智慧，感受數學對人類文明的重要性。

此外，數學家探索發現的故事可使學生體驗數學知識的發現過程，活躍課堂學習氣氛，調動學生的學習積極性。比如在學習等差數列前n項和時，教師可以先介紹一下高斯：在高斯小的時候，他的老師出了一道難題：1+2+3+…+100=？正當其他同學忙于把100個數逐項相加的時候，高斯很快就得出答案是5050。他的算法是把1+100，2+99，3+98，…，49+52，50+51，這樣湊成50組，那么答案就可以很快求出，是101×50=5050。

2.用數學實驗或游戲創設情境，讓學生體會數學的無窮樂趣

數學知識的學習是比較枯燥和抽象的，但是如果以實驗或游戲的形式，用探究的態度學習數學，那么數學知識就會變得讓人容易理解和接受，學生也更有興趣學習。這就需要教師在課前預先設計一些有趣的實驗或游戲，讓學生自己動手操作，在實驗過程中歸納、總結得出數學結論。下面我們看幾個以實驗或游戲為表現形式的情境設計。

案例一：課前讓學生準備半徑為R的半球（可以將乒乓球剪開，取乒乓球的一半），以及高和半徑都為R的圓錐和圓柱（用硬紙板制作高和底面半徑都與乒乓球半徑相等的圓錐、圓柱），還有一小袋沙子。課上讓學生先用半徑為R的半球裝滿沙子，又用高和半徑都為R的圓錐也裝滿沙子，并把這些砂子同時倒入高和半徑都為R的圓柱中。反復操作，可以發現砂子都剛好裝滿，于是，學生就會猜想容積一樣，也意味著體積相等，即V=V+V。在倒沙子的過程中，細心的同學會發現，當只把圓錐里的沙子倒入圓柱內時，沙子大概占圓柱的容積，若只把半球里的沙子倒入圓柱內時，沙子大概占圓柱的容積。實驗過后便可帶領學生學習圓柱和圓錐的體積公式，V=V-V=πR-πR=πR，所以就得到V=2V=πR，即為球的體積公式。

案例二：在講授隨機事件的概率時，可讓學生根據書上設計好的拋硬幣試驗，自己動手做試驗，并記錄下試驗的結果，而后教師再根據學生的試驗結果，提出問題，讓學生根據自己做的試驗進行討論，進而講授書上的內容。

案例三：在講古典概型前，讓學生準備兩個硬幣和一些一元的零錢，同桌兩人為一組，甲擺一游戲攤，由乙來參加游戲，游戲規則為：由乙同時拋兩枚硬幣，若都出現正面，則甲給乙2元，否則乙交游戲費每局1元。讓學生動手玩游戲，看看最后誰掙得的錢多，并互相交流探討結果是必然的還是偶然的。然后從實驗過渡到課本知識的講授，學生便會覺得“原來如此”，于是新知識便被學生輕松掌握了。

當學生親自參與了數學實驗或游戲后，對數學知識的實質有了感性認識，教師再進一步幫助學生透過現象觀察問題的本質，使得學生很自然地接受課本上的知識。

3.用實際問題創設情境，讓學生在感性認識中學習

數學源于生活用于生活，很多時候我們要解決實際問題，就需要從現實背景中抽象出數學模型，利用所學數學知識進行解答。而我們的大多數學生長期固化于兩點一線（家——學校）的生活模式，生活經驗的限制讓學生很少有機會感受數學對于生活的巨大作用。于是這就需要老師利用有限的課堂時間巧妙的創設情境，讓學生經歷“生活—數學—生活”這種知識的循環過程，進而促進學生在生活中發現和累積數學知識，培養分析問題和解決問題的能力。課堂上，教師適時地、富有啟發性地提問，可引導學生思考、探究問題，在不斷提問與回答中，收獲知識，培養能力。

例如，在上《向量》這節課時，我們可創設這樣的情境：借助多媒體演示一個緝私船和走私船的追逃問題。

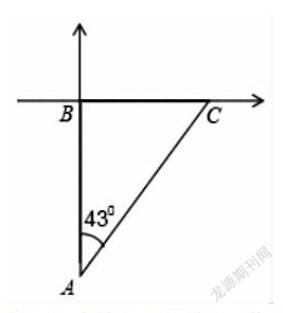
師：如圖，一艘海上緝私船在A處發現正北方向B處有艘可疑船只，該可疑船只正在向正東方向的C處航行，假如緝私船向北追去，能追上走私船嗎？為什么？

生：追不上！因為方向不對。

師：如果緝私船如果向東北方向追去呢？

生：還要看緝私船的速度和走私船的速度。

……

此類追趕問題是學生在物理課上常遇見的問題，教師通過引導學生思考，進而引出向量的概念：既有大小又有方向的量。而且教師還可借此問題，將數學中的數量、向量對比物理中的標量、矢量，使學生更深刻地理解向量的概念，從而達到突出重點、突破難點的教學目標。而且此追擊問題的背景還可運用于必修五的“解三角形”的授課中，等到學生學習解三角形時，只需將條件“緝私船向西南方向追去”稍作改變，使問題不但涉及方向，速度大小，還涉及角度計算等，那便是一道解三角形的題目了。

4.利用以舊帶新創設情境，引發學生的思維活動

孔子曰：“溫故而知新。”高中數學的學習更要注重知識的前后聯系，常常要通過對舊知識的復習提出新問題，引入新知識的講解。

例如，在講授線性規劃問題前，可引導學生回憶以前經常碰到利用不等式找最優解的問題。

已知服裝廠有甲、乙兩種面料，甲種面料70米，乙種面料52米。現計劃用這兩種面料生產A、B兩種型號的服裝共80套，已知做一套A型服裝需用甲種面料0.6米，乙種面料0.9米，可獲利潤45元，做一套B型服裝需用甲種面料1.1米，乙種面料0.4米，可獲利潤50元，當B型號的服裝為多少套時，所獲利潤最大？最大利潤是多少？

這種收益最大化問題我們可這樣去解：

解：設當B型號的服裝為x套時，所獲利潤為y元。據題意有：

0.6（80-x）+1.1x≤70（1），解之得x≤44

0.9（80-x）+0.4≤52（2），解之得x≥40

y=50x+45（80-x），即y=5x+3600

因為5>0且40≤x≤44，

所以當x=44時，y=5×44+3600=3820元。

但如果我們換一道題：某公司計劃2015年在甲、乙兩個電視臺做總時間不超過300分鐘的廣告，廣告總費用不超過9萬元，甲、乙電視臺的廣告收費標準分別為500元/分鐘和200元/分鐘，規定甲、乙兩個電視臺為該公司所做的每分鐘廣告，能給公司帶來收益分別為0.3萬元和0.2萬元。問該公司如何分配在甲、乙兩個電視臺的廣告時間，才能使公司的收益最大，最大收益是多少萬元？提出問題：這道題也是收益最大化問題，我們又該如何去解呢？引導學生列式：

解：設公司在甲、乙兩個電視臺做廣告的時間分別為x分鐘和y分鐘，總收益為z元，

由題意得

x+y≤300500x+200y≤90000x≥0y≥0

z=3000x+2000y

進而繼續講授線性規劃知識，利用線性規劃解題。這樣，我們便利用題目引導學生思考、探究，讓學生體會知識的前后聯系，利用復習舊知識過渡到學習新知識，使學生在接受新知識時，不會覺得突兀與生硬。并且通過問題的提出、問題的思考、問題的解決，體會探究式學習的快樂。

5.挖掘教材內容創設情境，開拓學生的學習空間

很多時候，我們的課堂教學就是把教材上的內容在課堂上對著學生講一遍，學生通過預習其實已經了解了課本內容，當他們在課堂上聽著老師再重述一遍時，便會覺得枯燥無味，同時也忽略了教材中隱含的豐富的數學思想，失去了鍛煉和提高思維能力的機會。這就要求教師上課不能只是照本宣科，而應根據不同的教學內容、教學目的，從學生的實際情況出發，對教學內容進行補充、加工、改編等，給予學生更大的學習空間，讓學生在認知經驗與教材結論發生碰撞的過程中，自主發現并學習新的知識，提高學生的數學思維能力。

如，在講授“等比數列前n項和”時，教材中直接利用錯位相減法推導出等比數列前項和的公式，此方法雖是求數列前項和的一種典型的方法，但學生并不會自己往這個方向去想，于是學生只是在上課時被動接受，課后強制記憶。那么學生便會產生疑問：在看課本之前我并不知道錯位相減法，那么我怎么求等比數列的前n項和呢？于是，教師可以引導學生從等比數列的定義出發進行推導：

∵==…=，∴==…=

由合比定理得：===q-1

所以當q≠1時，S===

由以上解法，我們又可以這樣想：

q===…===，

所以，當q≠1時，S=.

此外，我們還有更簡便的解法：

S=a+a+a+…+a=a+aq+aq+…+aq+aq-aq

=a+q（a+aq+…+aq）-aq=a+qS-aq

所以，當q≠1時，S=

雖然，錯位相減法是固然要介紹的，但教材經過教師的“二次創作”之后，可以拓展學生的思考空間，讓學生的認知經驗與教材的既定結論產生碰撞，從而促進學生認知的飛躍。

6.利用學科滲透創設情境，讓學生巧妙地聯系各科知識

我們知道學科間的關系是相互滲透的，物理中有數學知識、計算機課也需要數學知識等，學科之間的知識聯系和滲透不但可以幫助學生掌握學科知識，而且對于學生創新思想和創造能力的培養有著深遠的教育意義。

比如，在《三角函數的圖像與性質》這堂課的開始可以從熟悉的物理知識簡諧振動引入。物理中物體做簡諧振動時位移s與時間t的關系，交流電中電流i與時間t的關系，它們的圖像形如正弦函數的圖像，它們的函數關系都可以表示成形如y=sin（ωx+φ）的函數解析式。

再比如，我們也可以等學生在計算機課上學完編程之后，再安排上必修三第一章《算法初步》的課程，這樣學生學起算法來便會十分輕松。

逐步向前推進的高中課程改革，豐富了高中數學教學內容，對教師的課堂教學提出了更高的要求。我們通過精心設計教學情境，不僅培養學生的數學能力、數學思維，而且激發學生的學習熱情，增強學生的學習欲望。

參考文獻：

[1]高隆昌.數學及其認識.北京高等教育出版社，2001-10.

[2]張奠宙，宋乃慶.數學教育概論.北京高等教育出版社，2004-10.

[3]俞昕.數學教學呼喚“對話”.高中數學教與學，2009（1）.