巧用平移不變性，畫出正方體的展開圖

吳潔華

在學習簡單的立體圖形時，有一項很有意思的作業：畫出正方體的所有展開圖.每個同學都可以毫不猶豫地畫出開頭幾個，但要畫出所有11個不全等的展開圖，可真要動一點腦筋，否則不是漏掉了就是重復了，簡直毫無章法可言.我們在這里介紹一種做法，可以讓你有順序地畫出所有的正方體展開圖而不必記憶，甚至還可以發現不同展開圖之間是存在聯系的.

首先，我們不難畫出下面“T”字形的展開圖，除了標有數字1的另外的5個正方形可以拼成一個無蓋的正方體.讓方塊1在立體圖形上沿著A-B-C-D的位置連續翻轉，可以得到不同的展開圖.對應于左邊的展開圖，我們可以認為：方塊1沿著AD的方向平移，可以得到不同形狀的展開圖.我們把這個結論稱為“平移不變性”.

利用這個性質，我們每次改變一個正方形的位置，就可以得到幾乎所有正方體的展開圖.首先，讓方塊1和2改變相對位置，得到以下6種展開圖.

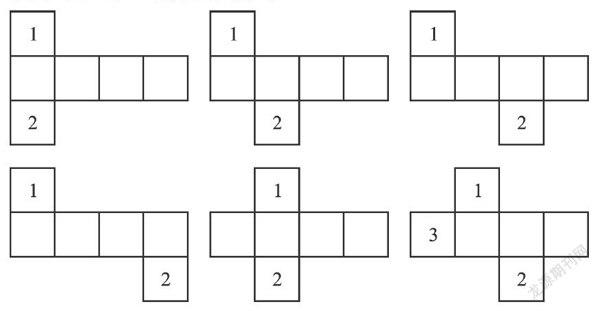
接下來，把上圖最后一個標號為3的正方體向上平移一格，得到下面的展開圖.

這個過程可以繼續進行，但要注意，每次只能平移一個方塊，且只能沿著棱的方向平移.

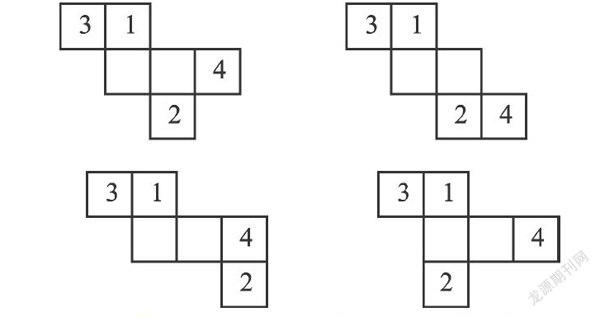
這樣，我們連續得到了正方體的10個展開圖，你會發現，這10個圖形之間可以互相通過我們這里所講的平移變換得到，因此不需要刻意去記憶它們的形狀.為了增強學習的體驗，建議同學們用幾張硬紙板做一下實驗.

最后，還有一個展開圖比較特殊，我們單獨畫在下面.

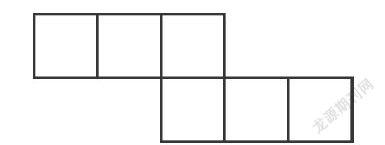
學習過程中，需要主動思考，發現問題的特征和規律.如果你不主動思考，沒有人會告訴你怎么辦，你也就享受不到學習的樂趣，體驗不了開發智慧的成就感，愿我們共勉！

（作者單位：江蘇省南師附中江寧分校）