火柴棒游戲

姜紅

一、 活動背景

荷蘭數(shù)學教育家弗賴登塔爾說：“數(shù)學學習是一種活動，這種活動與游泳、騎自行車一樣，不經(jīng)過親身體驗，僅僅靠看書本、聽講解、觀察他人的演示是學不會的.”我們的新課程標準中也提出了“基本活動經(jīng)驗”的新目標.其中還具體指出“學生應(yīng)當有足夠的時間和空間經(jīng)歷操作、觀察、模仿、實驗、猜想、驗證等活動過程“.所以說“動手實踐”也是學習數(shù)學的一種重要方式.

二、 實驗目的

通過動手操作與思考活動，提高對一些基本圖形的認識能力， 并滲透對“圖形運動”的理解，幫助同學們直觀感受幾何圖形.

三、 實驗準備與要求

準備火柴棒（或等長小木棒）若干. 本課實驗需要同學們按要求搭出符合條件的圖形. 在操作過程中要積極思考，并與同學交流. 實驗活動過程中不可以將火柴棒折斷，或者部分使用. 要用完整的火柴棒達到實驗要求.

四、 活動過程

在我們小的時候，會用火柴棒搭一些象形的圖案，從中我們享受了無窮的樂趣. 在小學里，我們又用火柴棒搭一些有趣的算式，如：移動一根火柴棒，使等式成立.

你知道該怎么移動嗎？

小小的火柴棒可以幫助我們學數(shù)學、增見識、長智慧.

1. 搭正方形

（1） 我們知道用8根火柴棒搭2個正方形；用7根火柴棒能搭2個正方形嗎？ 你是如何想到的？

通過思考不難回答，要面積不變而火柴棒根數(shù)變少，必須讓這兩個圖形共用某個邊，即從圖1變?yōu)閳D2.

（2） 把1根火柴棒的長度記為1，用12根火柴棒能搭出面積分別為4、5、8 、9的正方形嗎？

經(jīng)過嘗試可以搭成面積為4和9的正方形（如圖3、圖4），但是面積為5和8的正方形是搭不出來的.

那么把問題（2）的要求稍做變化，用12根火柴棒能搭出面積分別為4、5、8 、9的圖形嗎？去掉了正方形的限制，稍作思考即可知道，這是可以做到的，如圖5、圖6.

這兩個圖形還可以從計算上去驗證：

圖5中，面積為：5×1=5，周長為：（5+1）×2=12；

圖6中，面積為：4×2=8，周長為：（4+2）×2=12，故而均滿足要求.

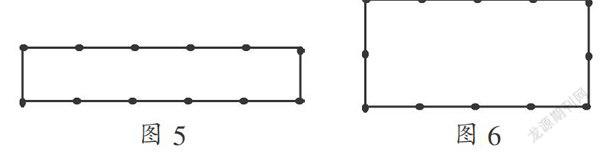
從另一個方面來想，既然已經(jīng)可以搭成面積為9的正方形，而面積為8、5的圖形沒有形狀限制，那么是否可以用減少其面積，但不減其周長來實現(xiàn)實驗目的呢？容易得出把圖4變?yōu)槿缦聢D7—圖13，其面積從9依次減少到3.

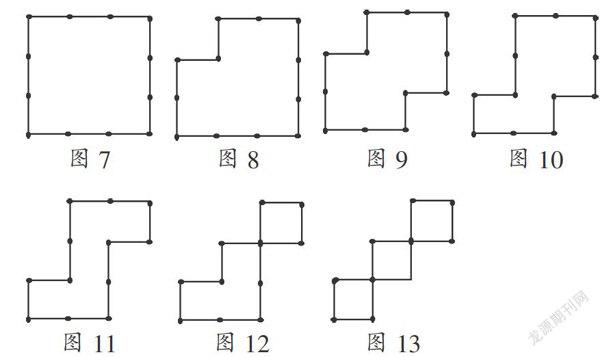
思考以上移動火柴棒的實驗，其本質(zhì)是線段的平移，因此其長度不變，但所圍成區(qū)域的形狀及面積卻發(fā)生了改變.

2. 搭三角形

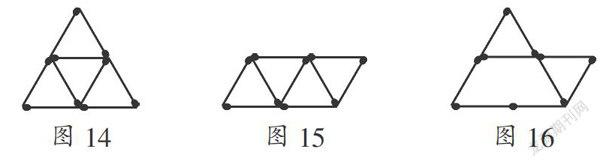
（1） 用9根火柴棒分別搭5個三角形、4個三角 形、3個三角形.其答案如圖14、圖15、圖16.（注意其中有部分是疊合在一起的）

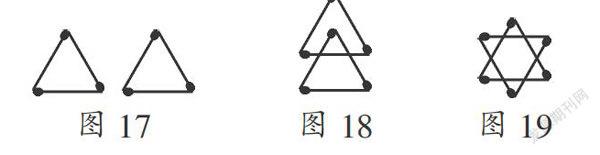
（2） 用6根火柴棒能搭2個三角形，如圖17，那么能搭3個三角形嗎？稍作思考可知不能，也不能搭出更多的三角形. 但是如果允許火柴棒交叉顯然就可以實現(xiàn)，如圖18中共有3個三角形、圖19中有8個三角形. 允許交叉是思維上的一次突破.

3. 數(shù)學思考

如果允許火柴棒搭成空間圖形或者交叉，顯然問題將更靈活、更發(fā)散，搭4個三角形最少只需要幾根火柴棒呢？如圖20，搭成一個空間里的正四面體，每個面都是三角形，但是只需要6根火柴棒； 搭5個正方形最少也只需要6根火柴棒，如圖21，注意其中有重疊哦.

19世紀英國著名數(shù)學家德· 摩根有這樣一句名言：數(shù)學發(fā)明創(chuàng)造的動力不是推理， 而是想象力的發(fā)揮. 本實驗從用火柴棒搭符合一定條件的正方形開始，到搭滿足要求的三角形以及其他圖形，再到數(shù)學思考，從平面視角到空間視角，我們能感受到小小的火柴棒蘊含著大智慧.善用數(shù)學實驗，變“聽”數(shù)學為“做”數(shù)學，通過做數(shù)學實驗體驗發(fā)現(xiàn)的樂趣，感悟數(shù)學真諦，在發(fā)展數(shù)學思維的同時提高實踐能力，相信同學們以后可以把數(shù)學學得更好.

（作者單位：江蘇省南師附中江寧分校）