生活中的一元一次方程應用

陳小云

數學來源于生活，生活中最基本的衣、食、住、行都含有數學元素. 隨著社會的發展，生活中的科學化、經濟活動中的最優化都需要人們運用數學知識、思想和方法. 一元一次方程雖簡單，卻是刻畫和研究現實世界數量關系的有效模型.初中數學教學大綱上明文要求學生會利用數學去解決實際生活中所遇到的問題，并且將生活中的實際問題描述為具備實際意義的數學問題. 現就一元一次方程在實際生活中的應用，從比賽、商品銷售、交通運輸、電費水費等日常生活中的四個方面舉一些常見例子.

一、 比賽類

例1 （2015·云南）為有效開展陽光體育活動，云洱中學利用課外活動時間進行班級籃球比賽，每場比賽都要決出勝負，每隊勝一場得2分，負一場得1分. 已知九年級一班在8場比賽中得到13分，問九年級一班勝、負場數分別是多少？

【分析】設勝了x場，那么負了（8-x）場，根據得分為13分可列方程求解.

解：設勝了x場，那么負了（8-x）場，根據題意得：2x+1×（8-x）=13，

解得：x=5， 8-x=3.

答：九年級一班勝、負場數分別是5和3.

【方法提升】解比賽類應用題的關鍵是設出勝的場數，以總分數作為等量關系列方程求解.

二、 商品銷售類

例2 （2015·江蘇泰州）某校七年級社會實踐小組去商場調查商品銷售情況，了解到該商場以每件80元的價格購進了某品牌襯衫500件，并以每件120元的價格銷售了400件.商場準備采取促銷措施，將剩下的襯衫降價銷售.請你幫商場計算一下，每件襯衫降價多少元時，銷售完這批襯衫正好達到盈利45%的預期目標？

【分析】設每件襯衫降價x元，根據銷售完這批襯衫正好達到盈利45%的預期目標，列出方程求解即可.

解：設每件襯衫降價x元，根據題意，得：

120×400+（120-x）×100=80×500×（1+45%），

解得：x=20.

答：每件襯衫降價20元時，銷售完這批襯衫正好達到盈利45%的預期目標.

【方法提升】解商品銷售類應用題的關鍵是弄清商品的進價、售價、利潤、折扣、利潤率等之間的數量關系，根據題目給出的條件，找出合適的等量關系列方程求解.

三、 交通運輸類

例3 甲乙兩人騎自行車，同時從相距65千米的兩地相向而行，甲的速度為17.5千米/小時，乙的速度為15千米/小時，經過幾個小時甲乙兩人相距32.5千米.

【分析】本題容易漏解，題中兩人相距32.5千米存在兩種情況，相遇前相距32.5千米或相遇后相距32.5千米，所以應進行分類討論.

解：設經過x小時兩人相距32.5千米，分兩種情況討論：

（1） 相遇前兩人相距32.5千米，根據題意得：17.5x+15x=65-32.5，

解得：x=1；

（2） 相遇后兩人相距32.5千米時，根據題意得：17.5x+15x=65+32.5，

解得：x=3.

答：經過1或3小時甲乙兩人相距32.5千米.

【方法提升】解決實際問題時要正確理解題目中給的已知條件中的不確定的數量、結論等，為保證答案全面、完整，需要分情況解決.

四、 電費水費類

例4 （2015·湖北省孝感）某市為提倡節約用水，采取分段收費. 若每戶每月用水不超過20 m3，每立方米收費2元；若用水超過20 m3，超過部分每立方米加收1元. 小明家5月份交水費64元，則他家該月用水_______m3.

【分析】20立方米時交40元，題中已知五月份交水費64元，即已經超過20立方米，所以64元水費由兩部分構成，列方程即可解答.

解：設該用戶居民五月份實際用水x立方米，

根據題意，得： 20×2+（x-20）×3=64，

解得：x=28.

故答案是：28.

【方法提升】在解水費電費分段收費類應用題時往往可以設其中一部分數量為x，然后表示出剩下的一部分數量，再根據水費電費數量關系列出方程求解.

五、 古代數學問題

例5 （2015·浙江嘉興）公元前1700年的古埃及紙草書中，記載著一個數學問題：“它的全部，加上它的七分之一，其和等于19.”此問題中“它”的值為_______.

【分析】設“它”為x，根據它的全部，加上它的七分之一，其和等于19列出方程，求出方程的解得到x的值，即可確定出“它”的值.

【方法提升】解古代數學問題時要抓住題目中出現的關鍵詞、能夠體現其數量關系的句子，將其轉化成數學語言，構建出數學模型，列出方程.

【試一試】

1. （2015·廈門）某商店舉辦促銷活動，促銷的方法是將原價x元的衣服以

x-10元出售，則下列說法中，能正確表達該商店促銷方法的是（ ）.

A. 原價減去10元后再打8折

B. 原價打8折后再減去10元

C. 原價減去10元后再打2折

D. 原價打2折后再減去10元

2. 學校組織一次有關世博的知識競賽共有20道題，每一題答對得5分，答錯或不答都倒扣1分，小明最終得76分，那么他答對_______題.

3. 父子倆在同一單位工作，父親從家到單位需用30 min，兒子走這段路只用了20 min，若父親比兒子早出發5 min，則兒子追上父親需要_______min.

4. 爺爺與孫子下了12盤棋（未出現和棋）后，得分相同，爺爺贏一盤記1分，孫子贏一盤記3分，則爺爺贏了_______盤，孫子贏了_______盤.

5. （2015·懷化）小明從今年1月初起刻苦練習跳遠，每個月的跳遠成績都比上一個月有所增加，而且增加的距離相同. 2月份、5月份他的跳遠成績分別為4.1 m、4.7 m. 請你算出小明1月份的跳遠成績以及每個月增加的距離.

6. 民航規定：乘坐飛機普通艙旅客一人最多可免費攜帶20千克行李，超過部分每千克按飛機票價的1.5%購買行李票. 一名旅客帶了40千克行李乘機，機票連同行李費共付1 170元. 機票的價錢是多少？

7. 請根據圖中給出的信息，求出大量筒中水的高度.

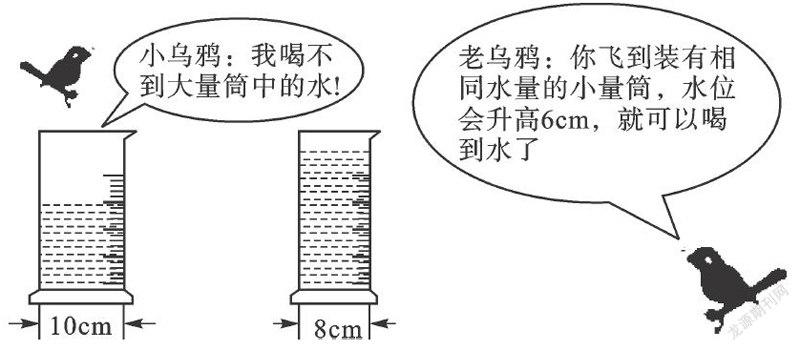
8. 古代數學問題：

巍巍古寺在山林，不知寺內幾多僧；

三百六十四只碗，看看用盡不差爭；

三人共食一碗飯，四人共吃一碗羹；

請問先生明算者，算來寺內幾多僧？

9. （2015·深圳）右表為深圳市居民每月用水收費標準.（單位：元/m3）

（1） 某用戶用水10立方米，共交水費23元，求a的值；

（2） 在（1）的前提下，該用戶5月份交水費71元，請問該用戶用水多少立方米？

10. 王剛到書店幫同學們買書，售貨員告訴他，如果花20元錢辦理會員卡，將享受八折優惠.

（1） 王剛預計要到書店買80元書，他是否值得辦卡？

（2） 在什么情況下，辦會員卡與不辦會員卡買書的費用一樣？

（3） 當王剛買標價共計200元的書時，怎么做合算，能省多少錢？

【參考答案】

1. B 2. 16 3. 10 4. 9 3

5. 解：設小明1月份的跳遠成績為x m，根據題意，得：4.7-4.1=3（4.1-x），解得：x=3.9. 則每個月的增加距離是4.1-3.9=0.2（m）.

答：小明1月份的跳遠成績是3.9 m，每個月增加的距離是0.2 m.

6. 解：設該旅客機票票價為x元，根據題意，得：x+（40-20）×1.5%x=1 170，

解得：x=900.

答：該旅客的機票價為900元.

7. 設大量筒中水的高度為x cm，根據題意，得：π×52x=π×42（x+6），解得：x=10.

答：大量筒中水的高度為10 cm.

8. 分析：山林中有一個古寺，寺里共有364個碗，平均三個僧人共用一個碗吃飯，四個僧人共用一個碗喝湯，試問寺中有多少個僧人？

等量關系：吃飯用的碗+喝湯用的碗=364，

解：設寺中有x個僧人，根據題意，得

+=364 ，解得：x=624.

答：寺中有624個僧人.

9. 解：（1） a=2.3.

（2） 設該用戶用水量為x立方米.

∵用水22立方米時，水費為22×2.3=50.6<71，∴x>22，∴22×2.3+（x-22）×（2.3+1.1）=71，

解得：x=28.

答：該用戶用水28立方米.

10. （1） 不值得辦卡；

（2） 當買標價為100元的書時，辦會員卡與不辦會員卡買書的費用一樣；

（3） 當王剛買標價共計200元的書時，辦會員卡合算，能省20元.

（作者單位：江蘇省如皋市實驗初級中學）