基于小波變換的多聚焦圖像融合算法研究

趙 慧

一、引言

一般情況下，成像系統無法對同一場景中不同距離的物體都形成清晰的像，因此圖像融合應運而生。圖像融合是將同一場景內的多幅圖像融合成一幅各處都清晰的圖像的過程。融合后的圖像能更好地適合人的視覺感知、滿足計算機處理的需求，而且能使圖像信息更全面地表現出來，進而提高圖像分辨率，使圖像更加清晰[1]。近年來已成功應用于目標識別與跟蹤、機器視覺以及醫學診斷等方面[2]。多聚焦圖像融合是圖像融合的一個典型的研究領域。

多聚焦圖像融合的方法可以分為兩大類，分別是基于空域的多聚焦圖像融合方法和基于變換域的多聚焦圖像融合方法。本文主要研究基于小波變換的多聚焦圖像融合方法，從小波變換的高頻域和低頻域兩個角度討論了幾種典型的多聚焦圖像融合方法，選擇不同的小波基函數對融合結果的影響也不相同。

二、多聚焦圖像的融合原理

由光學的成像系統理論可以得知，只有在物體齊焦(即物體處于物鏡的聚焦平面)狀態下，才能得到最清晰的成像，而當物體離開聚焦平面成像時，就會出現一定的模糊現象，所以成像模糊的程度與物體的位置是有直接關系的。通過調整鏡頭的位置來采集聚焦在物體不同點位的圖像序列。整個圖像序列包含物體在鏡頭中全部信息，每幅圖像都有聚焦清晰和聚焦模糊的區域，所以在圖像序列中獲得每個像素聚焦清晰的位置，通過一定的融合規則就能重建一幅清晰的圖像[3]。

三、小波變換分解的基本原理

小波變換是在空間(時間)上和頻率上的局部變換，是進行信號時頻分析和處理的理想工具。它是通過伸縮平移運算對信號(函數)逐步進行多尺度細化，最終達到高頻處時間細分，低頻處頻率細分，能自動適應時頻信號分析的要求，從而可聚焦到信號的任意細節。

二維小波變換通過利用兩個一維的濾波器對二維的圖像進行快速的小波分解，然后進行圖像重構，實現圖像的融合。用C0表示原始圖像f(x，y)，兩個一維的鏡像濾波算子設為H和G，分別用來表示低通和高通，依據Mallat的小波算法，尺度為j的分解公式如下:

此時，水平、垂直、對角方向的高頻分量分別用h、v、d來表示;H與G的共軛轉置矩陣分別用和H來G表示，與其對應的二維圖像的小波的重構算法如下:

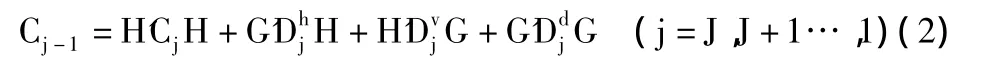
這里，J表示分解層數。

經過小波分解后，圖像高頻區域表示圖像的細節部分，反映的是圖像邊緣等信息;而圖像低頻的區域，則反映圖像的近似和平均特性。

四、基于小波變換的多聚焦融合算法

一幅圖像采取小波變換算法之后，絕對值比較大的小波系數與具有顯著變化特征的邊緣相對應，小波融合的低頻系數能夠決定圖像序列的輪廓部分(圖像變化平緩部分)。

對于源圖像運用層的小波分解，對其水平、垂直和對角方向的分量分別處理，將每幅圖像高頻系數在各尺度j(j=1～J)上分別對比，小波系數絕對值較大的分量對應圖像灰度值變化較大的邊緣部分的特征，人眼對于此類特征較敏感。因此，可以將對應位置上絕對值比較大的系數作為融合后圖像序列在小波域中的高頻系數[4]。

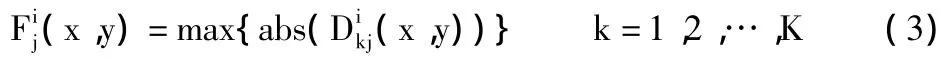
此時，多聚焦圖像序列數目用來K表示;i=1，2，3表示小波分解的系數(分別表示水平、垂直、對角三個方向的);第k幅圖像序列在點(x，y)處第j層的小波分解系數用來表示;abs表示對小波分解系數(x，y)的絕對值;對第個小波分解系數的最大值用max{abs((x，y))}來表示(x，y)表示融合的圖像序列在(x，y)處第j層的小波分解系數。

對于同一序列的多聚焦圖像，它低頻區域對應的數值是相同或者相近的，但是高頻區域的子圖像區別很大，所以說低頻系數在圖像序列中的平均值可以確定融合圖像的低頻分量，這種方法是基于小波變換的多聚焦圖像融合方法中常用的方法[5]。

若多聚焦圖像序列的數目用K表示，第k幅圖像序列在(x，y)處的第 j層小波分解低頻系數用 Ck，j(x，y)表示;第 j層的融合后的圖像序列的低頻系數用Cj表示，則:

通過小波變換的方法處理多聚焦圖像融合的過程中，小波基函數不是唯一的，采用不同的小波基函數會產生不同的融合效果。所以在進行圖像融合時不僅要選擇適合的高頻、低頻的融合算子，還要挑選出合適的小波基函數。常用的小波基函數有Haar小波、Daubechies小波(記為 dbN，N表示序號，下同)、Biorthogonal小波(bioNr.Nd)、Coiflet小波(CoifN)、Symlets小波(symN)。

五、多聚焦融合圖像的結果分析

評價多聚焦融合圖像的方法有主觀和客觀兩類評定法[6]。主觀評定是觀察者根據規定的評價尺度、個人經驗或參照標準圖像用目測法對融合圖像進行評定。而客觀評定法是利用一些量化的評價參數對融合圖像的質量進行判斷，可以提高判斷的速度和準確性。常用的客觀評價參數有信息熵、圖像均值以及標準差。

對于圖像I，設為圖像函數I(x，y)，M和N分別表示圖像的行數、列數。

(一)信息熵。熵指數用來衡量圖像信息的豐富程度，其大小反映了圖像中包含信息量的多少。如果把一幅圖像的各個像素都看成獨立樣本，則圖像灰度值的分布可表示成p={p0，p1，…，pi，…，pL－1}，pi表示灰度值是i的像素數和總像素數之比，L表示總的灰度級。根據香農理論，圖像的信息熵可表示為:

圖像的信息熵越大，表示融合后的圖像所含的信息越豐富，融合后圖像的效果也就越好。

(二)均值[8]。即圖像灰度的平均值，對于人眼則反映為平均亮度，若均值適中，則視覺效果良好。圖像的均值表示為:

(三)標準差[9]。圖像的標準差用來表示圖像灰度對灰度平均值離散的情況，在某種情況下可用來反映圖像反差的大小。圖像的標準差越小，圖像反差越小，對比度越小，無法看出太多的信息，而圖像的標準差越大，圖像反差越大，對比度越大，可以得到的信息就更多。圖像的標準差表示為:

其中μ為圖像灰度的均值。

對于目標圖像的三個參數值分別為E=7.0097、μ=118.7245、σ =62.3417。

本文對小波變換的多聚焦圖像融合方法進行研究，采用高頻系數絕對值最大法處理多聚焦圖像的高頻部分和低頻系數平均法處理多聚焦圖像的低頻部分，最后將處理后的圖像進行重構。圖1是多聚焦的序列圖像，對其采用小波變換融合后的圖像圖2所示。

圖1 聚焦清晰的區域不同的序列圖像

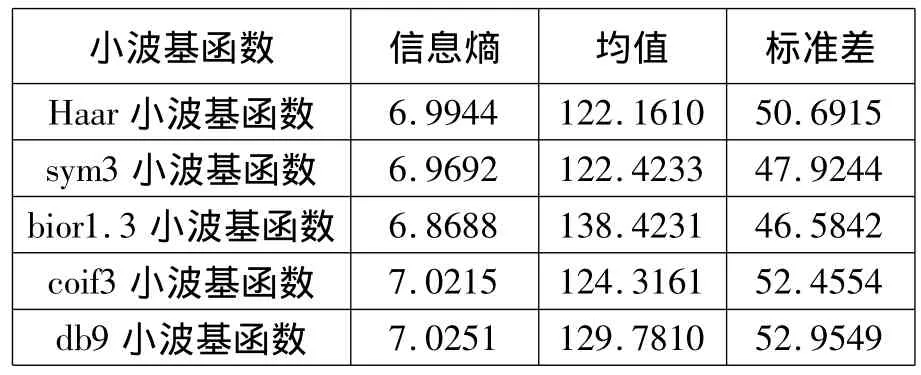
表1 采用小波變換融合方法對圖1處理結果的性能評價

采用三個評價參數對五種采用不同小波基函數融合后的圖像客觀評價如表1所示。將表1的數據與目標圖像的對應參數相比較，可以得出采用Haar小波基函數、sym3小波基函數和bior1.3小波基函數獲得的融合圖像的信息熵和標準差都偏小，不能獲得比較多的圖像信息;coif3小波基函數和db9小波基函數處理后的圖像目標圖像參數的差距最小。

六、結語

多聚焦圖像融合方法很好地解決了因為成像條件的限制，不能同時對同一場景中不同距離物體全部清晰成像的問題。本文利用小波變換對多聚焦圖像進行融合，主要介紹了高頻系數絕對值最大法和低頻系數平均法。分別采用了信息熵、圖像均值和標準差等參數作為本文的評價標準，對各個小波變換融合后的圖像進行性能評價。

[1]覃征，鮑復民，李愛國等.數字圖像融合[M].西安:西安交通大學出版社，2004

[2]韓冬兵.基于Depth form Focus的序列顯微圖像融合與三維測量技術研究[D].北京航空航天大學，2004

[3]陶觀群，李大鵬，陸光華.基于小波變換的不同融合規則的圖像融合研究[J].紅外與激光工程，2003，32(2):173 ～202