基于模糊技術的水下機器人運動控制

尹夢 舒 ，馮 常

（1.中國科學院光電技術研究所，四川 成都 610209；2.中國科學院大學，北京 100190）

0 引言

水下機器人這一高新技術對開發蘊含巨大資源的海洋有著不可小覷的功勞，因此發展水下機器人很有必要。現如今越來越多的地方用到水下機器人，如何控制好水下機器人來使其快速準確地完成人類派遣的任務就成為亟需解決的問題。而水下機器人工作環境的特殊性，也增加了對水下機器人控制的難度，因此水下機器人的控制系統需有較強的自調節能力以及在線模型辨識能力等[1]。

模糊控制技術（Fuzzy Control Technology）基于模糊數學理論，是近代控制理論中的一種高級新型技術[2]。它不需要過程的精確數學模型，魯棒性強，有較強的容錯能力，操作人員易于設計和掌握。本文以水下狀態檢查機器人為實驗平臺，其運動系統是非線性、時變、強耦合的，通常工作在幾米甚至更深的水下，受到各種未知因素的干擾[2]。由此看來，采用模糊方法控制水下機器人精準運動無疑是最佳選擇。

1 搭建運動模型

水下機器人在水中運動時會受到各種力和力矩的作用，研究在這些力和力矩的作用下水下機器人的運動規律，搭建水下機器人的運動模型，是研究和設計水下機器人控制系統的基礎[1]。

1.1 水下狀態檢查機器人的結構

本文以實驗室項目“水下狀態檢查機器人”為實驗平臺，水下運動主體如圖1所示。螺旋槳式水下運動平臺作為該系統的主體部分，配置了6個位置耦合的推進器，其中2個豎直方向推進器作為垂直推進，另外4個推進器作為平面運動及轉動推進，推進器對稱分布，確保水下機器人在運動時受力平衡，完成較精確定位。水下狀態檢查機器人通過自身的狀態檢查和陸上主控制器的算法控制，可實現水中的高穩定懸停和平穩的三維空間運動，其中運動的速度連續可調，潛浮運動時最大深度可達到30 m。

圖1 水下運動主體

1.2 水下狀態檢查機器人空間運動方程

使用六自由度的空間運動方程來表示實驗平臺在水下的運動狀態。為了使模型具有一般性，假設水下機器人重心G與載體坐標系原點O不重合，G在載體坐標 系 中 的 坐 標 為 xg、yg、zg[1]。

因此得到的六自由度空間運動方程如下[1]：

其中，m 表示水下狀態檢查機器人的質量；Ix、Iy、Iz是質量 m相對于載體坐標系各軸的轉動慣量；u、v、w、p、q、r 是其6個自由度的（角）速度是其6個自由度的（角）加速度；X、Y、Z、K、M、N 是其所受外力（矩）。

2 模糊控制器

模糊控制的核心在于運用模糊性的語言描述作為控制規則去執行控制，不同于傳統控制的理論和方法，模糊控制是以模糊數學為基礎理論建立的。

2.1 模糊控制系統組成

模糊控制屬于計算機數字控制的一種，一般由5部分組成：模糊控制器、輸入輸出端口、執行機構、被控對象和測量裝置，其系統框圖如圖2所示[2]。

圖2 模糊控制系統框圖

其中模糊控制器是控制系統的核心部分，它的一般組成如圖3所示，本控制器為多輸入多輸出模糊控制器，其由以下 4部分組成[2]：將語言描述轉換成表示模糊控制規則表中語言值的數學符號組成的規則庫；進行模糊推理來判決被控對象是否正常運行的推理機；接收控制器的輸入并轉換成推理機可接收參數的模糊化接口；接收推理機發出的模糊結論，并轉換成所需要的輸出值的反模糊化接口[2]。

圖3 模糊控制器的組成

2.2 模糊控制器的設計

在模糊控制器的設計過程中要考慮以下三個問題：模糊化輸入、建立語言控制規則和實數輸出。

2.2.1 輸入量的模糊化

集合X和Y分別表示輸入x和輸出u的論域，根據本文實驗平臺水下機器人的水下運動功能要求和實驗數據的分析，對模糊控制器選取位置偏差和速度偏差作為量 x，推進器所需的推力為控制量 u（t），其中位置偏差和速度偏差的論域分別為[-0.5 m，0.5 m]和 [-0.1 m/s，0.1 m/s]。

由于模糊化就是確定輸入量x在論域上的對應語言變量值，為了便于工程實現，通常要對論域實行離散化，即把輸入的論域進行歸一化處理。

采用Mamdani提出的標準化設計，將論域范圍設定為[-6，6]，將模糊控制器的輸入量的范圍離散化。例如輸入量 x的論域是[m，n]，則要將其量轉換為[-6，6]區間變化的量x′，采用如下公式[2]：

選取三角隸屬函數繪制語言變量取值分布圖，如圖4所示。

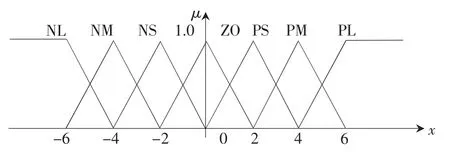
圖4 輸入的的隸屬函數

2.2.2 建立語言控制規則

模糊控制器的控制規則是基于人的思維推理的一種語言表示。模糊控制規則的具體形式為：If前件Then結論。將其輸入稱為前件，輸出稱為結論。這里需要注意，在制定模糊控制器規則時，前件可以不用含有所有的輸入，同時，規則庫中不能存在完全相同的兩條規則[2]。

模糊控制器的控制量應該遵循盡量消除偏差，但同時要保證系統的穩定性和防止系統超調。按照本課題實驗平臺的水下機器人的實際情況，當水下機器人的位置偏差和速度偏差都負大時，水下機器人處于規定的軌道方向較遠距離且還在偏航中，此時應該增大正的控制量，使水下機器人盡量回到正確軌道上來；而當水下機器人的位置偏差負大而速度偏差正大時，水下機器人處于規定的軌道方向較遠距離但偏差自身已有減小的趨勢，此時可以用較小的控制量幫助水下機器人按規定軌道行駛。通過選取合適的模糊條件語句，考慮水下機器人運動的實際情況，可得出如表1所示的模糊控制規則表。

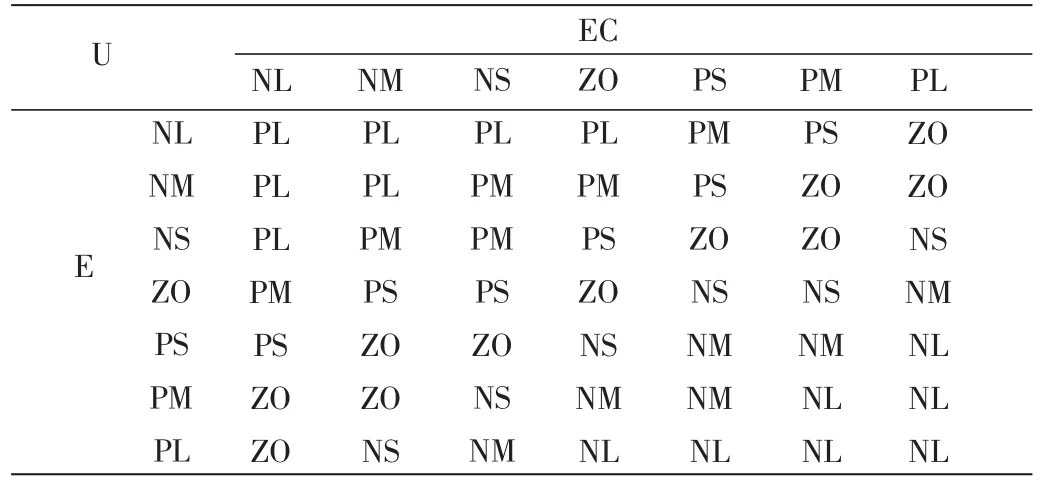
表1 模糊控制規則表

2.2.3 輸出量的反模糊化

模糊推理的結果不能直接用來作為被控對象的控制量，因為它是模糊的，所以還需要對結果進行反模糊化，轉換成可被執行機構實現的精確值[2]。反模糊化的目的是由模糊推理的模糊結論求出反映控制量的精確分布。目前，反模糊化的方法有很多，而本文采用的是重心法，也稱為質心法，它是所有反模糊化方法中最為常用和最合理的方法。其數學表達式如下：

上式的積分符號表示輸出模糊子集所有元素的隸屬度值在連續域y上的代數積分[2]，若模糊子集隸屬函數是離散域，則公式如下：

3 仿真結果及分析

根據已建立的水下機器人數學模型，創建仿真系統，利用本文設計的模糊控制器在仿真系統中進行定深潛浮實驗。給定參考輸入為4 m，系統初始狀態為零，采樣周期為0.1 s，控制器的輸出響應和運動響應如圖5和圖6所示。

由圖6可見，雖然剛開始時速度變化起伏很大，但當系統響應逐漸達到穩定狀態時，速度也趨于穩定。若采用PID控制器進行仿真實驗，則其系統響應與運動響應如圖7與圖8所示。

圖5 控制量仿真結果

圖6 線速度仿真結果

圖7 PID控制器的控制量的變化

比較這兩種控制方法的仿真結果，顯然在系統達到穩定之前，采用模糊技術的控制器速度起伏較大，但最終趨于平穩；而使用PID控制方法的仿真結果則不理想，隨著時間的推移，速度一直持續變化，而且輸出的控制量也在變化中，沒有平穩的趨勢。

4 結束語

本文以水下狀態檢查機器人為實驗對象，驗證了模糊技術應用于水下機器人的可行性，通過模糊控制器和PID控制器的仿真實驗結果的對比可看出，模糊技術在水下機器人運動控制上雖然較PID控制的系統超調微大，但對于系統穩定性方面來說，無疑是最好的選擇。現今模糊技術已得到廣泛的應用，尤其在處理那些非線性、強耦合時變或建模不易的系統時具有突出的優勢。但目前模糊控制理論并未達到成熟完善的地步，還需進行深入的研究。

[1]蔣新松，封錫盛，王棣棠.水下機器人[M].沈陽：遼寧科學技術出版社，2000.

[2]席愛民.模糊控制技術[M].西安：西安電子科技大學出版社，2008.