基于優化遺傳算法的股票選擇規劃研究
張金良
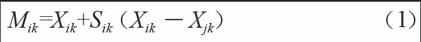

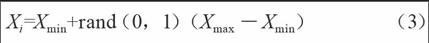
摘 要:最優股票選擇規劃方法在股民規避風險方面能發揮一定的作用。股市環境比較復雜,傳統的股民規避風險的方法應用在實際的股市中,往往會出現主觀性強、不穩定、風險大的缺點。為了避免上述問題,文章提出了優化遺傳算法的股票選擇規劃的方法。將自適應遺傳算法和貪婪算法很好的結合,獲取最優的投資方向,最大限度地為股民服務。實驗結果表明,利用優化遺傳算法實現最優股票選擇規劃,可在股票發生很大波動時,很好地規避風險,防止股民產生重大損失,最終有效提高了股民的收益。
關鍵詞:優化遺傳算法;股票選擇;最優規劃;規避風險
中圖分類號:TM714 ? ? ? ? ?文獻標識碼:A ? ? ? ? ? ? ? ?文章編號:2095-1302(2015)09-00-03
0 ?引 ?言
股票做為風險大、收益高的債券,在現在的社會中,很多人都把自己的一部分收入做為投資投入到股市中。股市的波動時刻影響著股民的切身利益,由于股市存在極強的波動性,使得人們對股市沒有很好的預測。規避風險的可能性很多,大多數股民都是通過自己的經驗和小道消息來選擇股票,這樣帶有一定的盲目性,從而給自己帶來一定的投資風險[1]。
但是隨著人們生活水平的不斷提高,手里的閑錢也越來越多,人們更愿意把手里的閑錢投入到股市中,但目前卻沒有一種很好的方法來使人們規避股市風險。為了避免上述弊端,提出基于優化遺傳算法[2-4]的股票選擇規劃方法,并對傳統算法和優化遺傳算法進行了比較,驗證優化算法的優點。
1 ?股票選擇規劃方法原理
在股民選擇股票的最優規避風險規劃過程中,可以將所有的股票做為蜜源成為初始集合,在該集合中,所有元素都能代表股民選擇股票規避風險過程中的解,所有解構成的集合是Xi(1,2,…,n),采用蜜蜂式搜索方式在類似區域內進行相同屬性個體的搜索,重復執行搜索模式,以獲取最優解。根據公式:
Mik=Xik+Sik(Xik-Xjk) ? ? ? ? ? ? ? ? ? ? ? ? ? (1)
對所有的股票選擇線路進行實時跟蹤監測,并對蜜源更新定位。設置j和k表示隨機選取的下標,且j∈(1,2,…,A),k∈(1,2,…,e)。Sik的取值范圍在[-1,1]之間,且Sik和Xik具有一定的關聯性,若監測系統搜索到股市里的股票有很好的適應性,漲幅穩定,則Xik的取值范圍越小。
在股民最優的股票選擇中,利用公式:
(2)
可計算具有穩定性的股票占股市總體風險的概率。其中,Ti表示第i個解的穩定值。
利用公式:
Xi=Xmin+rand(0,1)(Xmax-Xmin) ? ? ? ? ? ? ? ? ?(3)
可對單個蜜源進行優化練習,重復循環直至最優解產生為止,該解替換優化之前解所在的相應位置。
為了保證股票選擇路線的多樣性,利用公式(3)對控制端中具有強穩定性的股市中股民對股票的選擇路線進行變異處理,以便找出具有更強穩定性的選擇路線。具體步驟如下:
(1)應用迭代方法,按照一定規律對舊值變量進行不斷的遞推,從而得到新值。設置蜜源的初始迭代次數用Q表示,且Q=0,最大迭代次數用Qmax表示,最大限制次數為L。
(2)在蜜源中隨機選取N個股民的股票選擇線路,并利用公式(1)計算每個股民選擇股票的穩定值,根據每個股民選擇股票的穩定值能夠判斷該解的優越性。
(3)利用公式(2)計算具有強穩定性的股民選擇股票路線占總股民穩定性的概率Pi,根據概率Pi選擇最優蜜源,并記錄較優蜜源股票,對數據B位置進行實時更新。
(4)在仿真模型中,假如B(i)的值大于最大限制次數L的值,在解空間內進一步搜索,并記錄最優解的位置,保留在監測系統中。
(5)Q+1表示在Q基礎上進行一次迭代算法更新,當Q>Qmax時,記錄最優蜜源代表股民選擇股票路線的最優解。接著進行下一步驟操作。反之,當Q
(6)根據當前股民選擇股票穩定性規劃的最優解,可以很好地規避風險。
2 ?股民在選擇股票的最優穩定性股票的方法相關理論
利用傳統算法進行股市股民選擇股票的最優方法的規劃,建立的模型需要很多條件、耗時長。為此提出了基于優化遺傳算法的股票選擇規劃方法。
2.1 ?查找股民選擇最優股票的方法
根據遺傳算法對股民選擇最優股票的規劃進行運算。遺傳算法中交叉率PD和變異率PN決定股民選擇最優解,表達式:
(4)
(5)
在上述表達式中,hmax表示股民在選擇股票穩定性的最大適應度,havg表示股民選擇股票穩定性的平均適應度,h'表示參與交叉運算的兩個股民選擇股票穩定性的較大的適應度,h表示經過變異處理后股民選擇股票穩定性的適應度。設置j1,j2∈[0,1],j3,j4∈[0,1],分別表示交叉概率和變異概率的調整參數,在進行交叉運算后保留適應度最強的股票最優解。
提高計算效率,對交叉概率和變異概率進行優化處理,使Pd1>Pd2>Pd3,Pn1>Pn2>Pn3,且Pd1,Pd2,Pd3,Pn1,Pn2,Pn3∈[0,1],可以得到如下表達式:
(6)
(7)
由上式可得,隨機選取兩個不同股民的股票選擇路線做為交叉或者變異元素[5,6],在進行交叉和變異計算時,當兩個股民選擇股票中最大的穩定度值小于當前穩定值的平均穩定度值時,對于穩定值變異或者交叉概率的選擇,在最大和最小穩定度范圍之間進行最優求解。
2.2 ?股民選取穩定值最優的股票
由于股市環境存在一定的復雜性和風險性,使得自適應遺傳算法[7,8]建立的模型,具有一定的限制。而利用貪婪算法優化股民初始選擇股票的穩定值,就可以幫助股民最大限度地規避風險。假設股民有m個股票選擇,貪婪算法[9]的基本思想是:通過自己獲得的股票上市公司的一些資訊和國家政策導向,隨機選穩定值最優的股票,設為1,然后從余下(m-1)個股票選擇收益最高的股票進行對比。綜合各種外在條件,如果第(m-1)個股票的穩定值高于第m個股票,則用第(m-1)個股票代替第m條股票,將已經作比較的股票排除,依次進行選擇,生成新的個體。
3 ?仿真結果分析
為了更好的驗證優化遺傳算法的優越性,可選取一個股民五天時間里所選股票的真實走勢和優化遺傳算法的預測值的誤差。再利用傳統算法和優化遺傳算法的數據分析,就能夠得到表1和表2。
表1 ?傳統算法的數據表
時間(天) 股票真實走勢(%) 傳統算法預測走勢(%)
周一 -3.08 2.03
周二 -7.28 4.38
周三 1.72 -6.02
周四 0.81 7.92
周五 10 0.2
表2 ?優化遺傳算法數據表
時間(天) 股票真實走勢(%) 優化算法預測走勢(%)
周一 -3.08 -0.93
周二 -7.28 -5.72
周三 1.72 3.84
周四 0.81 -0.13
周五 10 8.02
通過兩種方法預測股票走勢和股票真實走勢值之間的誤差值比較,我們就可以更加清楚優化遺傳算法更接近股票的真實走勢。圖1所示是傳統算法和優化遺傳算法預測值與真實值比較的誤差率。
圖1 ?傳統算法和優化遺傳算法預測值與真實值比較的誤差率
通過比較能夠很好地得出,優化遺傳算法的誤差值在2%以內,而傳統算法的誤差值不穩定,因此優化遺傳算法的預測值更加接近股票的真實走勢,更有利于股民很好地規避風險并獲得收益的提高。
4 ?結 ?語
針對傳統對于股民選擇股票規劃算法需求滿足較多約束條件造成建模效果與真實值契合度較低的特點,提出基于優化遺傳算法的股民選擇最優穩定值的股票規劃方法,并對傳統算法和優化遺傳算法做了深入的比較,在此基礎上構建了新的股票選擇模型。經過對于股票穩定值的最優解分析,采用優化遺傳算法能更好地幫助股民規避風險,最大限度的保證了股民的利益。
參考文獻
[1]鄒萍.貨幣政策、股票流動性與資本結構動態調整[J].審計與經濟研究,2015(1):74-82.
[2]陳國良,王煦法,莊鎮泉,等.遺傳算法及其應用[M].北京:人民郵電出版社,1996.
[3] Back T.The Interaction of Mutation Rate,Selection and Self-Adaptation within a Genetic Algorithm[J].In:Parallel Problem Solving from Nature 2,North Holland,1992:84-94.
[4] Michalewicz Z, Janikow C Z,Krawczyk J B.A Modified Genrtic Algorithms for Optimal Control Problems[J].Computers Math Application,1992,23(12):83-94.
[5]熊軍,高敦堂,都思丹,等.變異率和種群數目自適應的遺傳算法[J].東南大學學報(自然科學版),2004,34(4):533-556.
[6]黎鈞琪,石國楨.遺傳算法交叉率與變異率關系的研究[J].武漢理工大學學報(交通科學與工程版),2003,27(1):97-99.
[7]金晶,蘇勇.一種改進的自適應遺傳算法[J].計算機應用與軟件,2006,23(2):108-110.
[8]王曉東,薛宏智,馬盈倉.基于自適應遺傳算法的神經網絡字符識別[J].西安工程大學學報,2008,22(2):211-213.
[9]李少芳.連續背包問題貪婪算法最優解的實現[J].福建電腦,2003(11):12-13.

